基于交織點改進彈簧-質點模型的緯編針織物動態變形模擬

常辰玉, 王雨薇, 原旭陽, 劉 鋒, 盧致文,2

(1.太原理工大學 輕紡工程學院, 山西 晉中 030600;2.安徽省天助紡織科技集團股份有限公司, 安徽 阜陽 236000)

緯編針織物是由一個個的線圈單元組成的,線圈單元的類型除成圈外還有集圈、浮線和移圈等,因為線圈單元組合的多樣性,以及不同線圈之間的穿套關系和牽拉作用導致緯編針織物的結構變形,從而實現了豐富的織物外觀。為建立合理的緯編針織物及其變形模型,并且實現動態模擬,可以做到對織物整體結構的控制以及對線圈結構細節的描述,從而預設織物形態、降低生產成本和提高生產質量。

對針織物進行建模的方法主要有基于幾何的方法和基于物理的方法:基于幾何的方法常用于均勻規則的織物,可以使用線圈單元的組合與排列進行模型的構造;而對于變形織物,由于會產生力的作用,使用基于物理的方法可以很好地描述織物的形變[1]。彈簧-質點模型具有描述直觀、實現簡單和計算速度快等優點,是出現較早且應用較廣泛的物理模型[2]:劉瑤[3]使用彈簧-質點網格模型和二維網格模型作為分析羊毛衫線圈變形的方法,通過測量相關偏移量獲得變形方程,但研究缺少對織物的受力分析;雷惠[4]以線圈根部所在位置將線圈設置為一個質點,建立質點模型而簡化彈簧-質點模型,并進行二維仿真;沙莎[5]提出立體化的彈簧-質點模型模擬組織結構較復雜的緯編針織物,模型復雜、運算量大、變形模擬時間長;汝欣[6]提出對應織物彈簧-質點模型初始狀態的確定方法,并建立了質點-控制點關聯式,實現密度非均勻分布的緯編針織物變形模擬,但缺少對不同線圈結構的變形模擬。目前關于緯編針織物形態的變形模型大都與能夠表示紗線路徑的結構模型相分離,造成了模型龐大、數據冗余的情況,因此必須探尋變形模型和結構模型之間的關聯,從而為緯編針織物及其變形建立簡單通用的模型,為實現動態模擬提供支撐。

本文通過建立線圈和緯編針織物組織的三維結構模型,探索線圈中心線的型值點和交織點之間的關系,依據交織點對彈簧-質點模型進行改進,使其更加適用于緯編針織物的變形,并基于結構模型和變形模型建立關聯模型,用NURBS曲線對線圈中心線進行繪制,對質點位置進行受力分析求解出織物變形過程,最后使用計算機工具展示關聯模型的動態模擬效果。

1 線圈結構模型

成圈是一種標準且典型的線圈結構,其它線圈結構都可以在成圈結構的基礎上通過變形得到。建立成圈的三維結構模型是豐富線圈結構模型的前提,同時為緯編針織物建立三維結構模型奠定了基礎。

1.1 基于交織點的線圈三維結構模型

線圈三維結構模型如圖1所示,使用實線線條表示線圈的表面輪廓,使用虛線線條表示線圈的中心位置,其中每個子圖中由左到右分別是相應模型的左視圖和主視圖,依據這2個視圖中的交織點位置和型值點位置可以建立相應模型的多角度視圖。

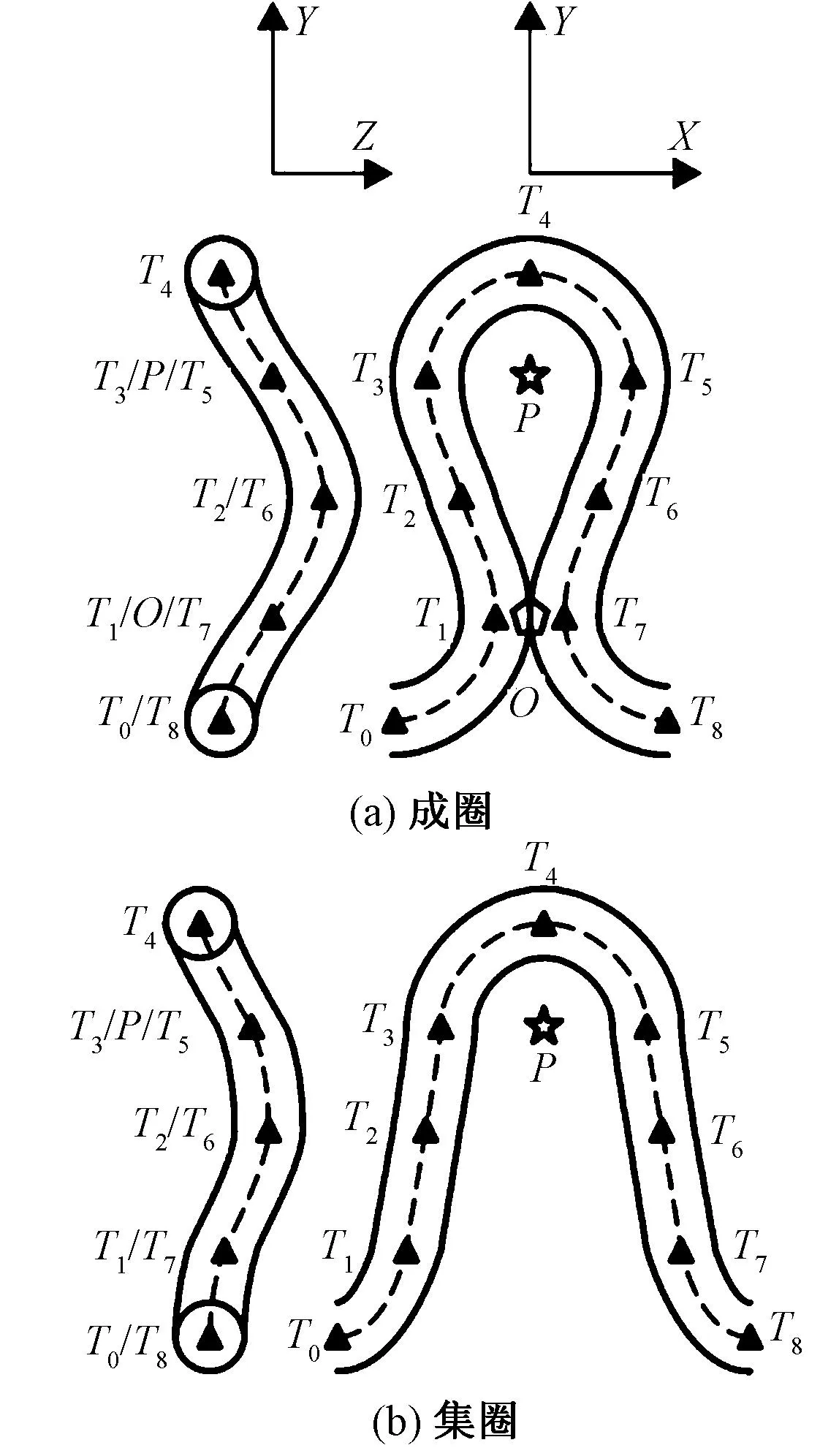
圖1 線圈三維結構模型Fig.1 Loop 3-D structure model. (a) Loop; (b) Tuck

線圈主要由圈弧和圈柱構成,圈弧根據所在位置和彎曲形態不同又分為針編弧和沉降弧,線圈頂部向上凸出的圈弧稱為針編弧,線圈底部向下凹陷的圈弧稱為沉降弧,而處于線圈中間位置的圈柱則上下連接針編弧和沉降弧。

根據成圈線圈對稱的幾何結構特點,使用數學幾何圖形建立其三維結構模型如圖1(a)所示。由于成圈線圈的針編弧與上一行線圈中的沉降弧穿套,成圈線圈的沉降弧與下一行線圈中的針編弧穿套,且圈弧位置受穿套影響較大,圈柱位置取決于圈弧,因此為精準表達線圈所在位置,在線圈相互穿套的中心處放置交織點[7],表示針編弧位置的上交織點如圖中星形P所示,表示沉降弧位置的下交織點如圖中五邊形O所示。由于成圈線圈左右對稱,且成圈線圈的左右部分又分別中心對稱,因此為了準確表示線圈結構形態,在線圈幾何路徑的關鍵處放置型值點,如圖中用三角點表示型值點位置,對稱點T2和T6標識左右圈柱中心處,同時也是線圈厚度方向最凸處,對稱點T1和T7標識圈柱與沉降弧連接處,同時也是線圈寬度方向最凹處,對稱點T3和T5標識圈柱與針編弧連接處,同時也是線圈寬度方向最凸處,對稱點T0和T8分別標識該線圈與左右相鄰線圈連接處,同時也是線圈高度方向和沉降弧最低處,T4標識線圈左右部分連接處,同時也是線圈高度方向和針編弧最高處,而T4分別與T0和T8關于T2和T6中心對稱,T3和T5分別與T1和T7關于T2和T6中心對稱。

為獲得其它類型線圈單元的三維結構模型,可以根據其對應的結構特點,對建立的成圈三維結構模型進行調整。例如集圈是一個因下半部分沒有穿套行為而未封閉的懸弧,因此其下交織點不存在,可以得到如圖1(b)所示的集圈三維結構模型。

1.2 緯平針織物組織三維結構模型

緯平針織物組織全部由成圈線圈整齊排列形成,外觀平整均勻,對其進行觀察分析并合理簡化,設定緯平針織物在靜態放置時線圈之間不存在擠壓變形和拉伸變形,線圈之間為均勻規則的貼合相連。將成圈的三維結構模型進行連續和穿套,形成緯平針織物的三維結構模型,如圖2所示。設線圈半徑為r;線圈寬度D由兩側各4r的沉降弧寬度組成,即4r+4r=8r;線圈高度H由4r的針編弧高度、4r的沉降弧高度和中間的圈柱高度組成,圈柱高度為上下2個交織點之間的距離,這個距離包含上一行線圈的沉降弧高度和下一行線圈的針編弧高度,由于二者在高度上存在1r的重疊,因此2個交織點之間的高度為3r+r+3r,從而線圈高度H為4r+3r+r+3r+4r=15r;線圈厚度M由2個2r的紗線直徑和預設1r的弧度縫隙組成,即2r+r+2r=5r。

圖2 緯平針織物三維結構模型Fig.2 3-D structure model of weft plain knitted fabric

2 彈簧-質點模型

在傳統彈簧-質點模型的基礎上,根據緯編針織物組織獨特的結構,基于交織點進行改進,從而形成更加適應于緯編針織物的彈簧-質點模型。

2.1 傳統彈簧-質點模型

彈簧-質點模型將緯編針織物排列有序的線圈假設為有質量的點,即質點;各個質點之間由彈簧相連接,用于表現線圈之間的相互作用。如圖3所示,傳統的彈簧-質點模型質點分布均勻,彈簧連接規律,結構彈簧連接經緯方向相鄰的2個質點,維持控制線圈經緯方向的受力,剪切彈簧連接斜向方向相鄰的2個質點,維持控制線圈斜向方向上的受力,彎曲彈簧連接經緯方向間隔的2個質點,維持控制線圈彎曲時的受力[8]。

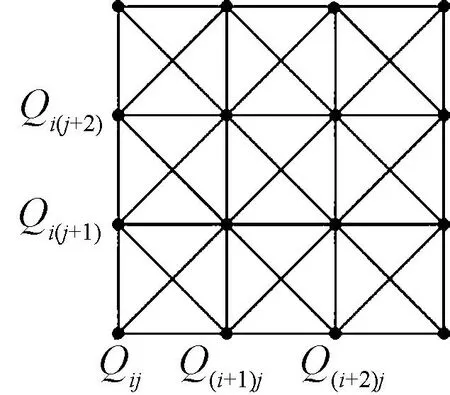
圖3 傳統模型Fig.3 Conven model

當針織物結構規則且均勻,如緯平針織物,可以使用傳統模型表達,但當線圈結構存在變化,不同的線圈單元按照一定規律或無規律的狀態進行組合時造成緯編針織物種類豐富多變,傳統模型無法體現,因此需要在傳統模型的基礎上進行改進以適應緯編針織物的多元化。

2.2 基于交織點的改進彈簧-質點模型

在模擬緯編針織物線圈結構豐富變化時,傳統的彈簧-質點模型不能改變質點之間的彈簧關系,因此,在傳統模型基礎上將線圈的交織點作為質點,將線圈與線圈之間的聯系作為彈簧,規則的模型即可成為可調節的模型。改進后模型的基本單元是單一的線圈結構,交織點即質點,同一線圈上下質點之間連接彈簧,稱為經向彈簧,用于表示線圈在經向的受力與走向,由于經向線圈折返,因此箭頭為雙向,相鄰線圈下方質點之間連接彈簧,稱為緯向彈簧,用于表示線圈在緯向的受力與走向,箭頭為單向,如圖4所示。

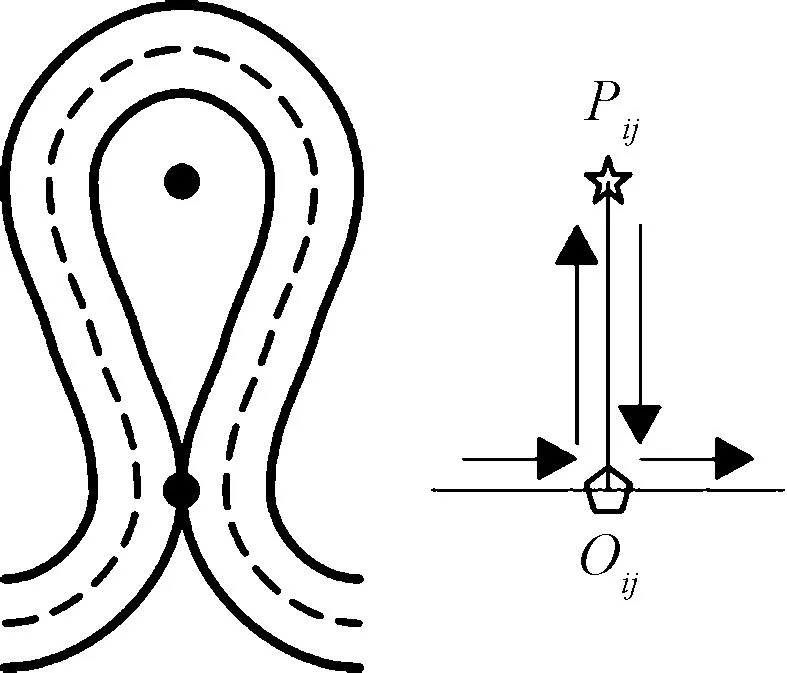
圖4 改進模型單元Fig.4 Improved model unit

線圈與線圈相互穿套,不考慮上下邊緣線圈,線圈的P點都與上方線圈的O點重合,2個質點聯動,位置統一,由此得到緯平針組織的改進彈簧-質點模型如圖5所示。改進模型的經緯彈簧本質為傳統模型中的結構彈簧,由于經緯彈簧可以間接體現剪切彈簧的受力,且本文不討論織物彎曲時的狀態,故舍去剪切彈簧和彎曲彈簧。

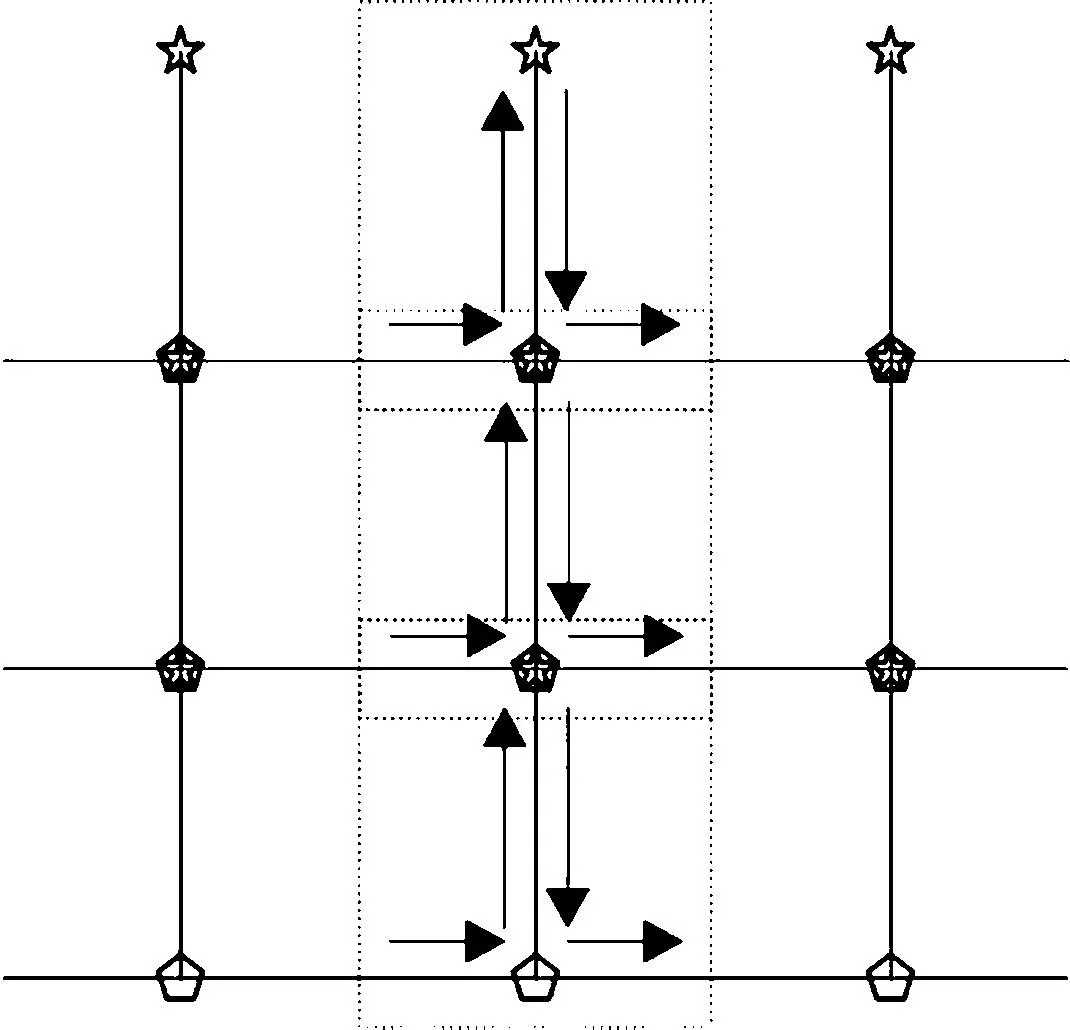
圖5 改進模型Fig.5 Improved model

當針織物組織中線圈類型發生改變時,交織點的位置和狀態同時改變,質點與彈簧也因此產生變化。如圖6所示的集圈改進模型,當成圈變為集圈時,線圈的下交織點Oij消失,只保留上交織點Pij,原本的經向彈簧和緯向彈簧結合后由Pij與O(i-1)j和O(i+1)j確定,同時,下一行線圈的上交織點Pi(j-1)上移到上交織點Pij的位置,導致線圈被拉長。同理,進行其它類型的線圈變化時,可以根據其幾何結構和紗線連接關系,得到相應的改進彈簧-質點模型。

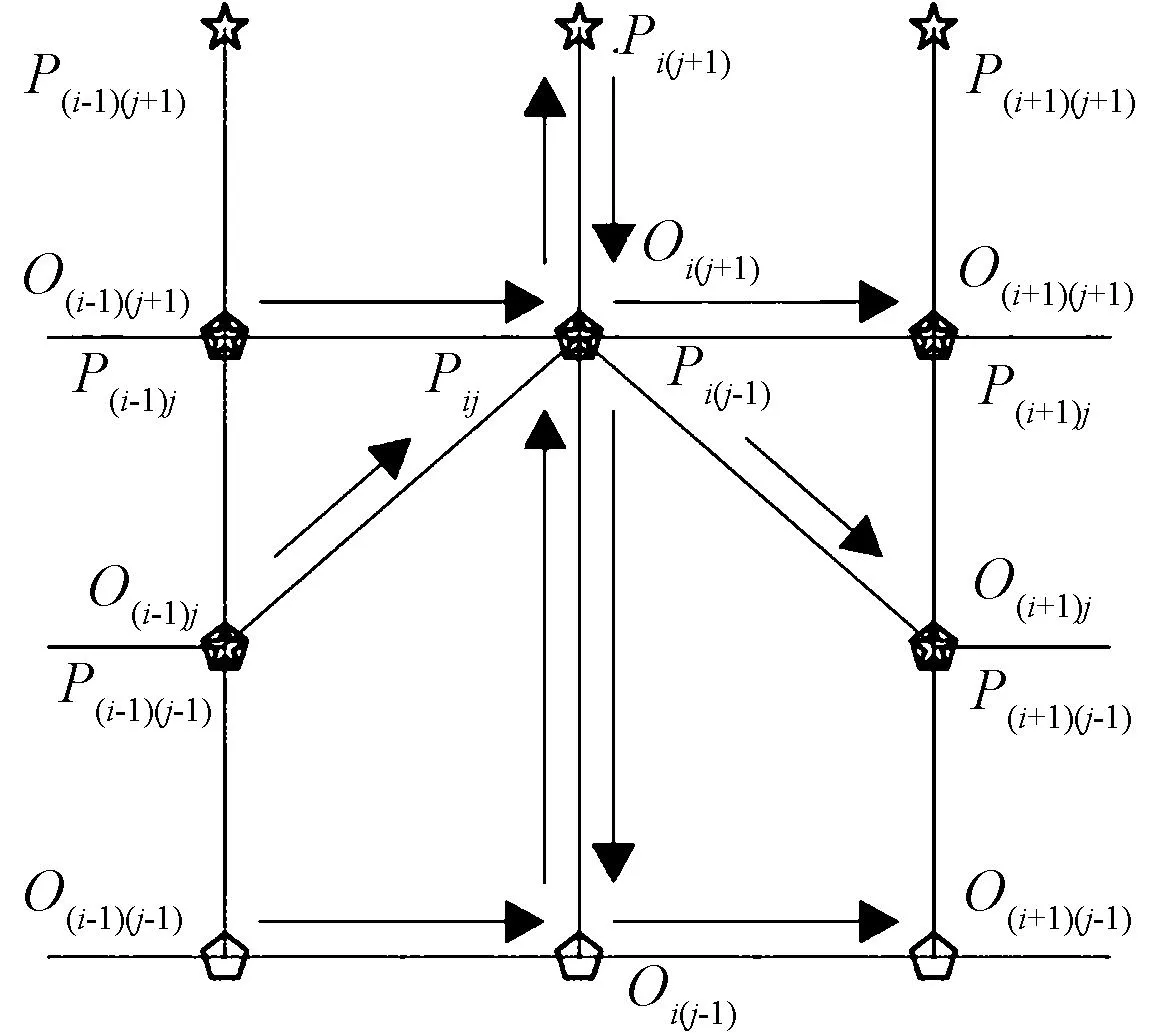
圖6 集圈的改進模型Fig.6 Improved model of tuck

3 動態變形模擬的實現

在結構模型和變形模型以及交織點的基礎上建立關聯模型,線圈中心線由NURBS曲線擬合,對質點進行受力分析求解更新位置數據,動態表達織物結構的變形過程。

3.1 關聯模型

設置線圈半徑、行列數和類型獲得織物大小和結構,從而得到每個交織點的狀態和位置;然后以交織點作為參照得出線圈型值點,用于擬合線圈中心線,并根據交織點即質點的原則放置經緯彈簧,建立織物的彈簧-質點系統,進而關聯結構模型和變形模型。

3.2 NURBS曲線

NURBS曲線可以由分段有理多項式矢函數來描述:

式中:

其中,權因子wi與控制點Ai一一對應,Ni,k(u)為k次規范B樣條基函數,被節點矢量U=[u0,u1,…,un+k+1]的計算結果所確定[9]。

在實際應用時,NURBS曲線的獲得分為2種情況:正算是已知控制點,求解型值點并繪制曲線形狀;反算是已知型值點,求解相應的控制點來擬合通過型值點的曲線[10]。在本文研究中,建立型值點與交織點的關系函數后,可以通過交織點的狀態和位置計算得到相應型值點的位置,進而反算出控制點的位置,最后基于控制點數據擬合出線圈中心線。

3.3 受力分析與動力學求解

當緯編針織物中因不同類型線圈單元的存在而導致結構變形時,能夠表示線圈位置的交織點(即質點)會發生相應的位移,由于交織點(即質點)之間經向彈簧和緯向彈簧的存在,交織點(即質點)受力產生速度和加速度,并獲得新的位置,直到織物結構趨于穩定。緯編針織物的變形,主要是由于線圈穿套關系改變導致的內部牽拉作用引起的,因此僅對內力進行分析,忽略外力的影響,進而進行動力學求解。

彈簧力Fs與阻尼力Fd相加之和約等于質點所受的內力。使用胡克定律可以獲得彈簧力的關系式為

Fs=-KsL

式中:L為彈簧形變矢量,即彈簧伸縮前后的長度變化量,在本文研究中,等同于交織點(即質點)與所連接彈簧另一端交織點(即質點)之間的距離矢量變化量;Ks為彈性系數。阻尼力的關系式表達為

Fd=-KdV

式中:V為質點的速度矢量,在本研究中,等同于交織點(即質點)的速度矢量;Kd為阻尼系數。質點受力與加速度之間的聯系式由牛頓第二定律確定為

F=Fs+Fd=ma

式中:a為質點的加速度;m為質點的質量,可由針織物的總質量分配給交織點(即質點)得到。

在進行動力學求解時經常用到2個方法:歐拉法和Verlet積分法,其中歐拉法又包括顯式、隱式和半隱式3種方法。相比而言,歐拉法的實現過程較為簡易,但誤差不易控制,在計算精度和計算效率方面,Verlet積分法則明顯占優,所以動力學求解選擇使用Verlet積分法:

式中:X(t)為t時刻質點的位置矢量,V(t)為速度矢量,a(t)為加速度矢量,Δt為時間間隔。

4 結果與分析

圖7示出運用C++編程語言、CodeBlocks集成開發環境以及OpenGL函數庫,實現仿真模擬程序的工作流程步驟。首先是依據結構模型和變形模型所需的數據,對程序進行初始化設置;然后在這些數據的基礎上對交織點、型值點以及控制點進行計算;之后對彈簧-質點模型和線圈中心線分別進行繪制;最后對模型不斷地進行受力分析和動力學求解更新質點(即交織點)位置直至系統達到穩定狀態。

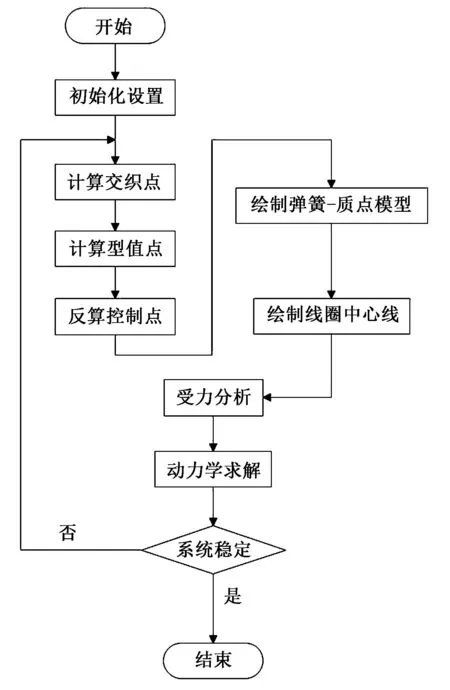
圖7 程序流程圖Fig.7 Program flow

在不考慮紗線立體粗細和表面紋理等實際因素的前提下,使用線圈中心線表示紗線路徑,緯平針織物組織中幾何結構模型和物理變形模型的關聯模型模擬效果如圖8(a)所示,圖8(b)示出某線圈改成集圈結構但未進行受力分析前的關聯模型模擬效果,然后,隨著模型受力發生變化以及質點位置的移動,通過受力分析模擬出其動態變化,其過程如圖8(c)所示,最終到達模型的穩定狀態,如圖8(d)所示。

圖8 關聯模型的動態模擬Fig.8 Dynamic simulation of associated model. (a) Weft plain knitted fabric; (b) Change a loop to a tuck; (c) Dynamic changing time; (d) Steady state time

圖9、10分別示出包含多個集圈和多個浮線的織物組織模擬效果。

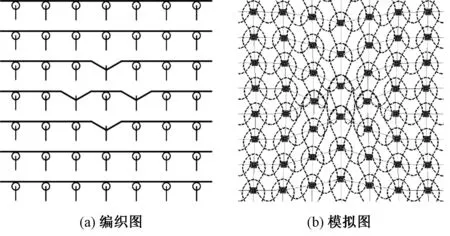
圖9 包含多個集圈的織物組織變形模擬Fig.9 Simulation of fabric structure with multiple tucks. (a) Knitting diagram; (b) Simulation diagram

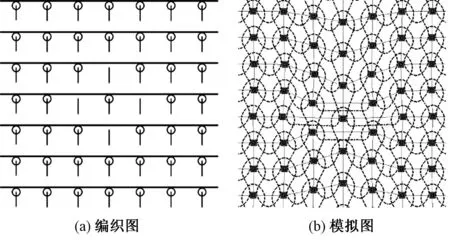
圖10 包含多個浮線的織物組織變形模擬Fig.10 Simulation of fabric structure with multiple misses. (a) Knitting diagram; (b) Simulation diagram

通過分析圖8～10中的模擬結果可以得出:建立結構模型和改進變形模型的方法具有可靠性,提出的關聯模型具有可行性,采用的模型繪制方法和計算方法對緯編針織物的動態變形模擬過程具有良好的支撐作用。

5 結 論

本文通過建立線圈和緯編針織物組織的三維結構模型,探索了線圈中心線上型值點和交織點之間的關系,為其它基本線圈結構單元和復合織物組織的三維結構模型提供了確立基礎;為使變形模型更加符合緯編針織物,基于交織點改進了現有的彈簧-質點模型,并且提供了具有集圈變形織物的變形模型示例;在建立關聯模型后依據型值點反算出控制點繪制線圈中心線,對質點位置和狀態進行受力分析,求解出最終穩定狀態,實現動態變形模擬;舉例展示了緯平針織物組織中更換基本線圈單元前后、動態運動過程中和最后穩定狀態時的關聯模型模擬效果,并且舉例展現了包含多個不同類型線圈的織物組織變形模擬效果。