垂直管內高質量流速超臨界CO2換熱特性

朱兵國，鞏楷剛，彭斌

（蘭州理工大學機電工程學院，甘肅 蘭州 730050）

近年來，我國一直貫徹新發展理念、推動高質量發展，積極參與國際社會碳減排，順應全球綠色低碳發展潮流，制定了“2030 年前碳排放達峰”行動方案，提出了“2060 年前實現碳中和”遠景目標。超臨界二氧化碳（S-CO2）循環發電技術由于其在系統緊湊性、高效率、適用性、靈活性等方面具有無可比擬的優勢得到了國際上的廣泛關注，成為順應時代背景的熱點課題[1-3]。此外，在“雙碳”任務的背景下，探索先進的發電技術能夠有效地提升能源利用率、構建低碳和清潔安全的能源體系，而S-CO2動力循環發電系統是有效提升能源利用率的先進技術之一[4-5]。

Jiang等[6-7]對S-CO2在加熱微型管內的對流傳熱特性進行了一系列實驗和數值模擬研究，重點闡述了運行參數、浮升力及流動加速效應等對微型加熱管內S-CO2傳熱的影響，結果表明：S-CO2傳熱受入口溫度、運行壓力、熱流密度、管徑以及質量流速等參數的影響較大。劉生暉等[8]開展了豎直圓管內S-CO2強迫對流傳熱特性實驗研究，實驗結果表明：在S-CO2在豎直向上流動中，由于浮升力增強使得S-CO2從強迫對流傳熱過渡至混合對流傳熱，最后發展為自然對流傳熱，傳熱能力也由弱化逐漸到恢復直至強化；然而流動加速效應則抑制S-CO2傳熱能力。G?kkaya 等[9]開展了0.509mm 微管內SCO2向上和向下流的對流傳熱實驗，結果表明：不論向上還是向下流動，S-CO2對流傳熱特性主要受浮升力影響。Guo 等[10]對超臨界壓力CO2在垂直加熱管內的對流傳熱特性進行了數值模擬，建立了變湍流普朗特數SSTk-ω湍流模型，分析了擬臨界點附近的質量流速、熱流密度、管徑、入口溫度和浮升力對超臨界壓力CO2傳熱的影響規律。王柯等[11]對S-CO2在垂直微細管道內的傳熱特性進行了數值模擬，發現增大質量流速可以減小壁面邊界層厚度，從而強化換熱；此外由于重力和浮升力作用的綜合影響，導致流動方向可以影響S-CO2傳熱性能。Kline等[12]實驗研究了超臨界壓力CO2在垂直向上流動加熱管中的對流傳熱特性，發現傳熱惡化的發生與入口溫度有密切關系。當入口溫度小于擬臨界溫度，內壁溫度將會急劇升高，即發生傳熱惡化現象；當入口溫度大于擬臨界溫度，內壁溫度單調上升，則屬于正常傳熱現象。吳新明等[13]對S-CO2在圓管內流動時的壓降和摩擦系數進行了實驗研究，發現摩擦壓降隨著質量流速和壓力的增加而顯著增加，而熱流密度對摩擦壓降的影響較小。王乃心等[14]對S-CO2在不同管道內的對流傳熱特性試驗進展做了研究，歸納得出：垂直管道內與異形管道內的S-CO2對流傳熱特性的研究相比水平管內更加匱乏。

綜上所述，盡管目前研究者們對S-CO2對流換熱進行了大量研究，但這些研究都是在中低質量流速下進行的，傳熱特性受浮升力的影響較大，而文獻[15-16]中可以找到不一致的結果，浮升力和流動加速效應的評判標準并不能廣泛適用。此外，在實際工程中，例如S-CO2燃煤發電循環，由于熱力學要求，S-CO2燃煤發電系統的循環流量是水蒸氣機組的6～8倍[5]，導致S-CO2鍋爐正常的運行工況參數大部分是處于高質量流速的條件下。朱兵國[17]建立了超高參數CO2對流傳熱實驗系統，彌補了實驗數據的不足，但質量流速也主要集中在1000kg/(m2·s）附近，由于隨著質量流速的提高，實驗需要的加熱功率在不斷增大，對實驗條件提出了更高的要求，從而缺乏高質量流速條件下管內S-CO2對流傳熱特性的實驗研究。數值模擬作為超臨界流動傳熱研究的重要手段，不僅可以彌補實驗的不足還可以獲取到詳細的內部流場信息。因此，本文因利用數值模擬開展了高質量流速條件下S-CO2在不同管道內的對流傳熱特性的研究，分析了不同參數對傳熱的影響，通過內部流場信息來揭示換熱機理，建立適用于高質量流速條件下的新型傳熱關聯式，此項工作也將更好地幫助研究者理解超臨界流體傳熱機理，對S-CO2循環發電動系統的設計也具有重要意義。

1 模型和方法

1.1 物理模型

圖1展示了本文研究的垂直圓管物理模型，管長為2800mm，包含入口絕熱段L1=500mm、有效加熱段Lh=2000mm和出口絕熱段L2=300mm，內徑din=10mm。其中入口絕熱段是為了確保CO2流至加熱段處已經充分發展，避免入口效應對數值模擬產生影響；出口絕熱段是為了防止回流影響計算精度。流動方向沿z軸的正方向，重力方向與流動方向相反。本文主要研究S-CO2在垂直圓管內對流換熱的特性，管壁厚度并不會影響流體域的研究，故忽略管壁厚度。

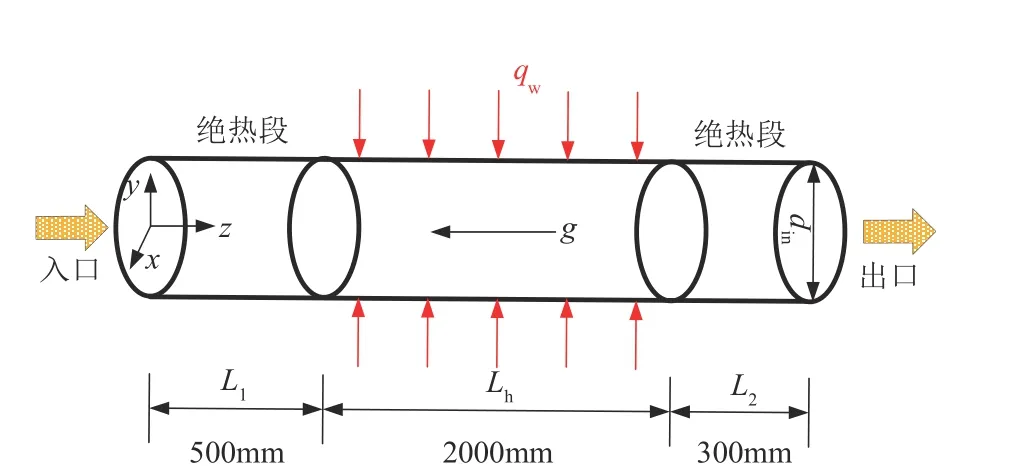
圖1 物理模型

1.2 數值方法

眾所周知，網格對其熱物性的捕捉至關重要，也是探索S-CO2管內對流傳熱特性的關鍵。因此，為了很好地捕捉到劇烈變化的熱物性引起的管內S-CO2復雜流動傳熱特性，本文對靠近壁面的區域網格進行了加密處理。已有研究表明在超臨界流體流動傳熱數值計算中，對SSTk-ω湍流模型，流體域內靠近壁面第一層網格量綱為1高度y+需滿足y+＜1[18]，來保證低雷諾數湍流模型的計算要求。

基于壓力求解器求解控制方程，采用有限體積法對控制方程離散，離散格式采用二階迎風算法，對壓力速度耦合方程采用SIMPLEC 算法求解。能量項的亞松弛因子設定為0.85，其余保持默認值。為了獲取到準確的CO2物性，計算過程中采用NIST實際氣體模型。當質量方程和動量方程的最大殘差值小于10-5、能量方程方程的殘差值小于10-6且內壁溫度不隨迭代次數變化時認為計算收斂。質量守恒方程、動量守恒方程和能量守恒方程[19]在直角坐標系下分別表示為式(1)～式(3)。

質量守恒方程

式中，u為速度矢量，m/s；ρ表示密度，kg/m3；μ為黏度系數，Pa·s；h為比焓，kJ/kg；重力加速度g取9.8m/s2，Prt為湍流普朗特數；下角標i、j取1、2、3 時分別代表x、y、z三個不同的方向。

為了更好地闡述S-CO2管內對流換熱特性，則必定需要管內S-CO2詳細的對流傳熱信息，而選用合適的湍流模型是數值模擬計算的關鍵，因此本文基于眾多研究者[19-21]對湍流模型（Standardk-ε、RNGk-ε、AKN、YS、LS、AB 和SSTk-ω）的研究基礎上開展了對比試驗，對不同的湍流模型進行了評估及選取。

關于Standardk-ε、RNGk-ε、AKN、YS、LS、AB 和SSTk-ω湍流模型輸運方程表達式及相關常數項和函數項詳細信息可參考文獻[19]。

截面主流溫度Tb和主流焓值ib分別定義為式(4)和式(5)。

傳熱系數h表示為式(6)。

式中，Tw為內壁溫度，℃；Tb為主流溫度，℃；A為垂直圓管流體域截面面積，m2；qw為壁面熱流密度，kW/m2；i為焓值，kJ/kg；cp為定壓比熱容，kJ/(kg·℃)。

2 結果與討論

2.1 湍流模型的優選

圖2 展示了在壓力p=8.221MPa、質量流速G=1001.5kg/(m2·s)和熱流qw=244.33kW/m2的惡化工況條件下，采用七種不同的湍流模型進行數值模擬計算，預測垂直加熱管內S-CO2的對流傳熱特性。通過與文獻[22]的實驗數據對比，由圖2 不難看出七種湍流模型均能預測加熱條件下S-CO2管內傳熱惡化的發生，且惡化點全都發生在擬臨界焓值之前。但AKN、YS 和AB 模型明顯將壁溫預測過高，而LS、Standardk-ε、RNGk-ε和SSTk-ω均較好地預測惡化溫度，但在惡化點前LS、Standardk-ε和RNGk-ε均低估了實驗測量壁溫，在擬臨界焓值后同樣也低估了實驗測量壁溫，僅有 SSTk-ω湍流模型預測的壁溫與實驗數據幾乎重合，趨勢也幾乎一致。

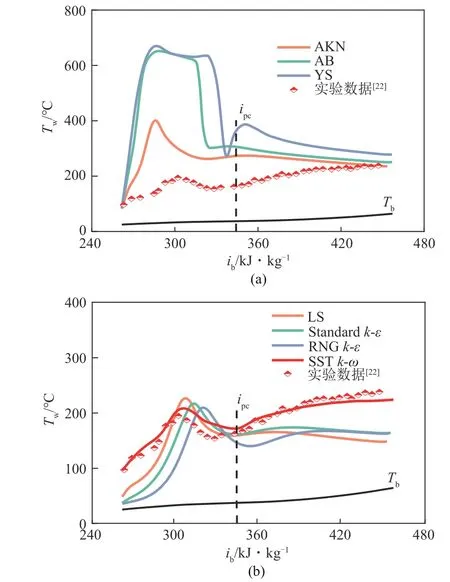
圖2 不同湍流模型計算結果與實驗數據對比[p=8.221MPa，G=1001.5kg/(m2·s)，qw=244.33kW/m2]

2.2 網格獨立性驗證及模型驗證

網格數量過多將會浪費計算資源，過少則將會導致不能夠很好地捕捉物性信息，因此選擇合適的網格數量不僅有利于提高計算效率還可以保證計算精度。故本文對圓管網格劃分進行了網格獨立性驗證，如圖3 所示，采用四種網格節點數不同的模型進行了網格獨立性驗證。不難看出當網格中的節點總數大于250 萬時，隨著節點總數的增加，計算結果沒有顯著的偏差。在當前研究中，因此最終確定網格節點總數為250 萬個。由前文可知，SSTk-ω湍流模型可以很好地預測SCO2管內對流傳熱規律，為進一步驗證湍流模型的可靠性和準確性，選用文獻[17]中的惡化工況及正常工況，建立相同的物理模型，對其數值模擬結果與實驗結果進行了比較。如圖4 所示，數值計算結果與實驗結果吻合良好。因此，該模型可以用于數值模擬計算高質量流速條件下均勻加熱管內S-CO2對流傳熱特性。

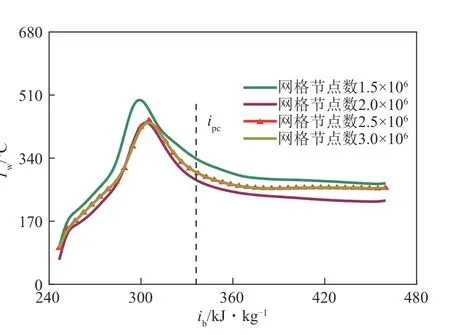
圖3 網格獨立性驗證[p=8MPa，G=1500kg/(m2·s)，qw=400kW/m2，Tin=20℃]

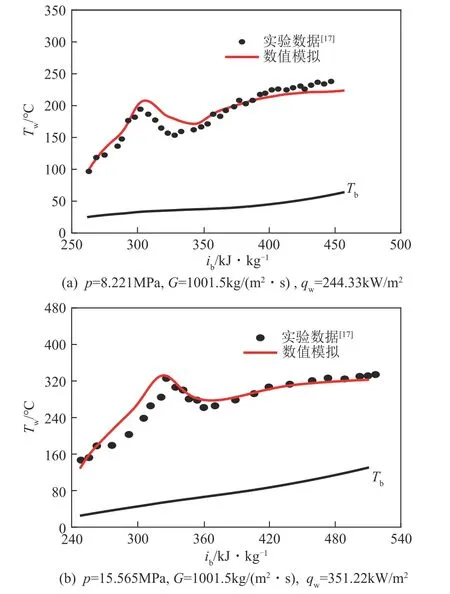
圖4 數值模擬計算與實驗數據的比較

2.3 運行條件對高質量流速S-CO2 管內換熱的影響

2.3.1 入口溫度

圖5 展示了壓力p=8MPa、質量流速G=1500kg/(m2·s)和熱流密度qw=400kW/m2的工況條件下入口溫度對內壁溫度的影響。如圖5 所示，在相同的壓力、熱流密度和質量流速下，當入口溫度低于擬臨界溫度時，在擬臨界點之前觀察到顯著的溫度峰值，這表明發生了傳熱惡化（HTD）。此外，隨著入口溫度Tin的增加，壁溫的峰值向出口高焓值區移動，當入口溫度高于擬臨界溫度時，壁溫單調增加。從上述觀察結果可以看出，在高質量流速和高熱流密度的條件下，超臨界壓力下的傳熱特性受到入口溫度的顯著影響，而HTD 與入口溫度也緊密相關。

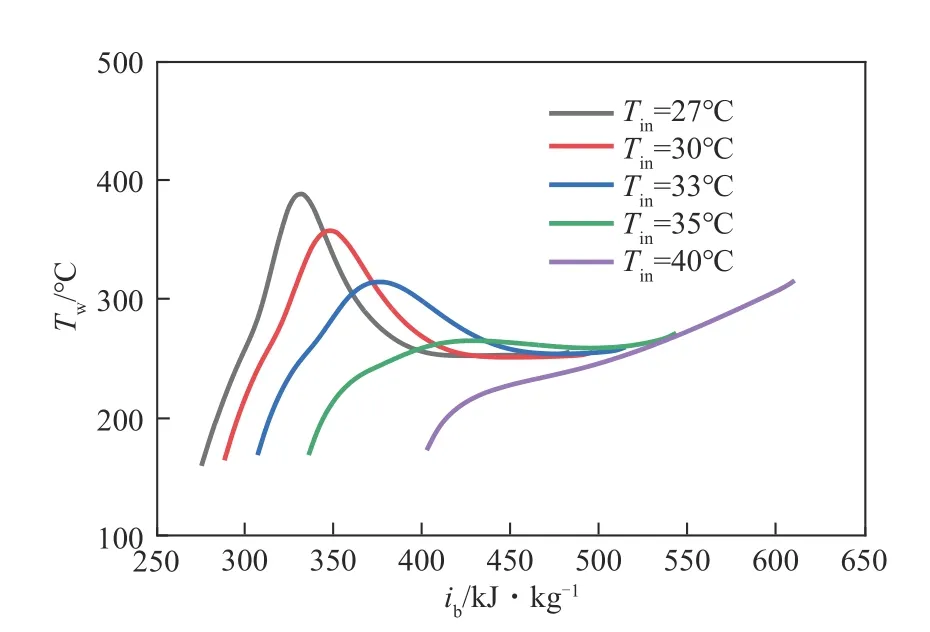
圖5 入口溫度對壁溫的影響數值模擬計算與實驗數據的比較[p=8MPa，G=1500kg/(m2·s)，qw=400kW/m2]

2.3.2 運行壓力

圖6 展示了質量流速為G=1500kg/(m2·s)、入口溫度Tin=25℃和qw=400kW/m2的工況條件下運行壓力對壁溫影響。從圖6中可以觀察到壓力對傳熱特性的影響也非常重要，當壓力為8MPa 時，壁溫發生了突然上升又下降現象，產生了HTD；但當壓力達到10MPa 時，壁溫峰值明顯降低，壁溫峰值點也向出口方向移動；當壓力達到15MPa 時，壁溫則是隨著主流焓值逐漸升高，HTD 現象并未發生。因此，在高質量流速和高熱流密度條件下，增大壓力可以抑制甚至消除HTD的發生。

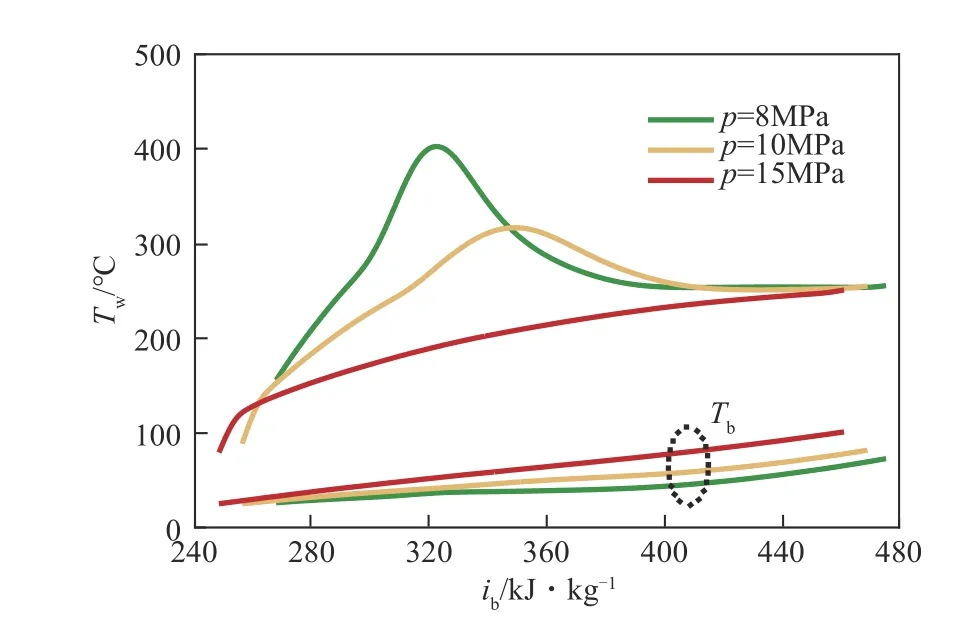
圖6 壓力對壁溫的影響[G=1000kg/(m2·s)，Tin=25℃，qw=400kW/m2]

2.3.3 熱流密度

圖7 展示了壓力p=8MPa、質量流速G=2000kg/(m2·s)和入口溫度流Tin=25℃的工況條件下熱流密度對壁溫的影響。當qw=200kW/m2時，壁溫隨主流焓值的增加平穩上升，并未發生壁面溫度異常增大或減小，此現象屬于正常傳熱。但是當qw=400kW/m2時，壁面溫度出現了較小的峰值，即在高熱流密度的條件下也發生了微弱的傳熱惡化現象。此外，一個有趣的現象是隨著熱流密度的增加，主流焓值ib也是逐漸增大，壁面溫度也逐漸升高。總而言之，高質量流速條件的確有利于傳熱，但是當熱流密度也較高時，HTD 依舊可能發生。

2.3.4 質量流速

圖8展示了壓力p=8MPa、熱流密度qw=400kW/m2和 質 量 流 速G=1000～2500kg/(m2·s)下 質 量 流 速 對S-CO2傳熱的影響。如圖8所示，在加熱條件下，壁面溫度受質量流速的影響較為顯著，壁面溫度隨質量流量的增加反而大大降低。當G=1000kg/(m2·s)和1500kg/(m2·s)時壁面溫度出現了顯著的峰值，但在G=2500kg/(m2·s)時，壁面溫度單調增加，表明較高的質量流速可以消除HTD并改善傳熱。

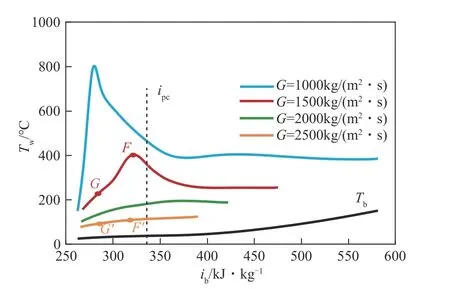
圖8 質量流速對壁溫的影響（p=8MPa，qw=400kW/m2，Tin=25℃）

2.4 傳熱機理

2.4.1 浮升力

浮升力是指當超臨界流體流入加熱管時，由于超臨界流體在擬臨界溫度Tpc附近熱物性變化劇烈，徑向較小的溫度差也會引起徑向較大的密度差，徑向密度差導致形成強浮升力，浮升力改變近壁區流體流場的分布，進而影響剪切力和湍流動能等的分布，最終導致傳熱的異常現象。Jackson[23]提出了垂直管道中S-CO2浮升力效應開始的標準數Bu。Bu數可以利用式(7)和式(8)進行計算。

描述垂直管道浮升力效應的另一個標準數Bu*可以利用式(9)和式(10)進行計算[23]。

Jackson[23]提出，當Bu＞10-5時，浮升力對超臨界流體傳熱有顯著影響，但是當Bu＜10-5時，浮升力對傳熱的影響可以忽略不計。Jackson 等[24]認為，當Bu*＜5.6×10-7時，浮升力效應較弱，對S-CO2傳熱規律的影響很小。

在p=8MPa、qw=400kW/m2、G=1000～2500kg/(m2·s)時，研究了浮升力對S-CO2傳熱的影響。圖9 顯示了Bu和Bu*在不同質量流速下的變化。隨著質量流 速 從1000kg/(m2·s)增 加 到2500kg/(m2·s)，Bu和Bu*明顯下降。這表明浮升力的作用隨著質量流速的增加而減弱。

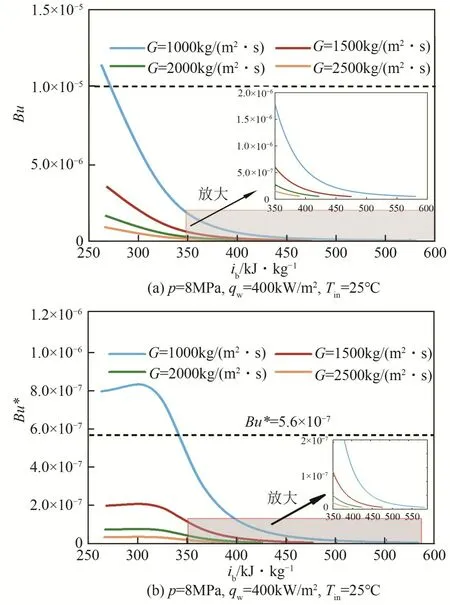
圖9 不同質量流速下的浮升力變化

更重要的是，在四種不同的質量流速下，只有G=1000kg/(m2·s)時，在低焓值區Bu＞10-5，其他則在整個焓區都小于10-5；對于Bu*而言，同樣只有在低焓值區Bu*＞5.6×10-7。上述結果表明，當質量流速較高時，浮力效應對S-CO2傳熱的影響較小，浮升力不能很好地解釋高質量流速下S-CO2管內傳熱機理。

2.4.2 流動加速效應

Mceligot等[25]提出了采用Kv來表征流動加速度效應，其中Kv的計算如式(11)。他們認為當Kv＜3×10-6時，則不考慮流動加速效應對S-CO2對流傳熱特性的影響。

在p=8MPa、qw=400kW/m2、G=1000～2500kg/(m2·s)時，研究了流動加速效應對S-CO2傳熱的影響。圖10反映了不同質量流速下Kv隨主流焓值變化的分布，不難觀察到流動加速效應隨質量流速的增加而減小，但是在四種不同質量流速下，在垂直圓管內的整個主流焓區，Kv均小于3×10-6，說明高質量流速下流動加速效應對S-CO2傳熱也沒有影響。

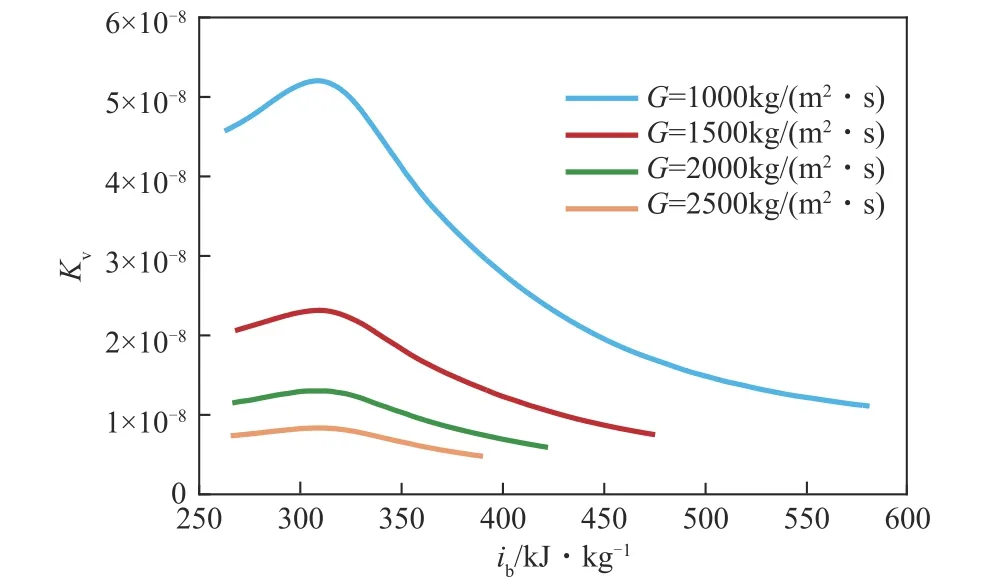
圖10 不同質量流速下的流動加速效應的變化（p=8MPa，qw=400kW/m2，Tin=25℃）

2.4.3 類沸騰理論

浮升力和流動加速效應并不能很好地解釋高質量流速下管內S-CO2的對流傳熱機理，因此為了更好地闡述高質量流速下管內S-CO2的對流傳熱特性，本文基于類沸騰理論，結合管內流體的熱物性和流場分布，揭示高質量流速下S-CO2傳熱機理，闡述傳熱惡化原因。與亞臨界流體并不相同，超臨界流體類沸騰發生在一個有限的溫度區間[T-,T+]，其中T-為相變起始溫度，T+為相變終止溫度。T-和T+可以由式(12)～式(14)確定[26]。

式中，cp,L為類液相的參考比熱容，取為cp（p=pc，T=0.75Tc）；pc為臨界壓力；Tc為臨界溫度；TL為類液參考溫度，取為0.75Tc；i0,L為類液參考焓，取為i（p=pc，T=0.75Tc）；cp,V為類氣參考比熱容，取為cp（p=0，T=Tc）；TV為類氣參考溫度，取為Tc；i0,V為類氣參考焓，取為i（p=0，T=Tc）；cp,pc為擬臨界點比熱容；Tpc為擬臨界溫度；ipc為擬臨界焓。

根據式(12)～式(14)可以求到兩個交點，交點即為T-和T+的值。圖11展示了超臨界類沸騰傳熱模型，當超臨界壓力下的“過冷”流體流入垂直加熱管時，如果溫度Tw＜T-管內流體則為純類液流體；如果溫度T+＞Tw＞T-＞Tb，那么主流核心區為類液相，近壁區為類兩相；當Tw＞T+時，近壁區為類氣相，壁面附近形成一個類氣層；而Tb＞T+時，管內流體為純類氣流體，而類液類氣共存于有限溫度區間[T-,T+]之間。

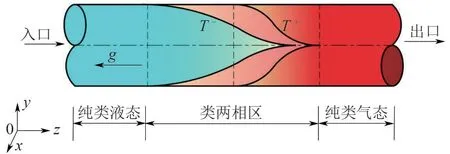
圖11 超臨界類沸騰傳熱模型

由于類氣相具有像空氣一樣的低熱導率，因此厚的類氣層會導致較大的熱阻，這將嚴重抑制熱量從管壁到主流區的擴散，最終導致內壁溫度急劇升高，發生HTD。然而，當入口溫度高于擬臨界溫度時，主流為純氣態流體，傳熱特性符合單相對流傳熱，因此內壁溫度隨著主流焓值的增大單調升高。為了進一步探究造成傳熱惡化的原因，選取圖7中的4個特征截面G、F和G'、F'進行分析，解釋質量流速導致S-CO2傳熱產生差異的主要原因，闡述S-CO2對流傳熱機理。

圖12展示了上特征橫截面G、F和G'、F'處的熱物性和湍流在徑向上的詳細分布，標記了T+的徑向位置，類氣膜厚度δ定義為T+徑向位置到管內壁的距離。如圖12 所示，特征橫截面G處的類氣膜厚度大于特征橫截面G'處的類氣體膜厚度，特征橫截F處的類氣膜厚度遠大于特征橫截F'處的厚度。換而言之，隨著質量流速的增加，類氣膜厚度逐漸減小。由于類氣膜的低熱導率和近壁區類氣膜的低熱吸收能力[圖12(a)、(b)]，因此在特征截面G處和F處傳熱能力減弱。圖12(c)展示了密度在徑向方向上的分布，不難發現，近壁區主要被類氣流體占據，而類液流體主要集中主流核心區。除了類氣膜厚度和類氣膜熱物性外，近壁區的湍流動能對傳熱也有很大的影響。如圖12(d)所示，近壁區的湍動能在高質量流速下比在低質量流速下高得多。即隨著質量流速的增加，近壁區較薄的類氣膜和更大的湍流動是傳熱增強的主要原因。綜上所述，超臨界S-CO2傳熱受類氣膜厚度、類氣膜熱物性和近壁區湍流動能的影響較大。

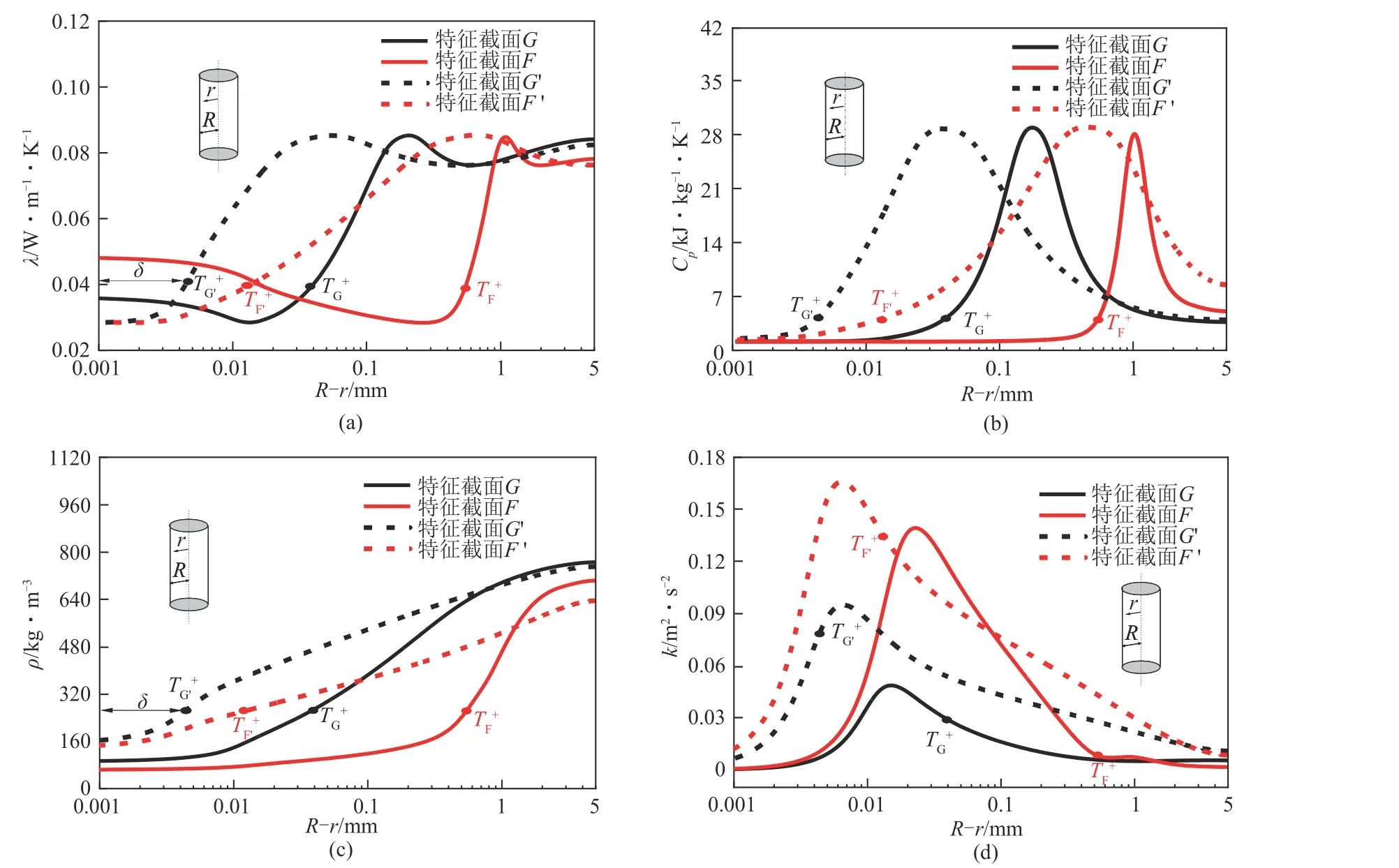
圖12 特征界面徑向熱物性和湍流的分布

2.5 高質量流速條件下傳熱關聯式的建立

眾多研究者通過熱物性參數，將浮升力和流動加速效應因子等進行量綱為1 排列組合，對Dittus-Boelter 型關聯式進行優化處理。Zhu 等[22]對亞臨界沸騰和超臨界傳熱進行了相似性分析，提出了超臨界沸騰數SBO 用來預測傳熱惡化的起始點，驗證了SBO 數的有效性。本文中存在大量的惡化數據，因此引入SBO 數擬合關聯式。基于數值模擬及文獻[17]數據建立超臨界壓力二氧化碳數據庫，利用最小二乘法對各種無量綱數的排列組合進行選代尋優，得出了新的超臨界壓力二氧化碳傳熱關聯式。式(15)和式(16)為擬合所采用的方程形式。

式中，cp為定壓比熱容，kJ/(kg·K)；μ為黏度，Pa·s；λ為熱導率, W/(m·K)；i為焓值，kJ/kg；G為質量流速，kg/m2s；d為管直徑，m；C為系數。

采用多變量線性回歸方法確定C與n1～n5的系數，得到式(18)。

為了檢驗SBO 傳熱關聯式與文獻中廣泛引用的五個關聯式（表1）的精度，采取平均相對誤差（eA）、平均絕對誤差（eR）和均方根相對誤差（eS）來定量評價傳熱關聯式的預測精度。對于參數F，單個數據點的誤差為式(19)。

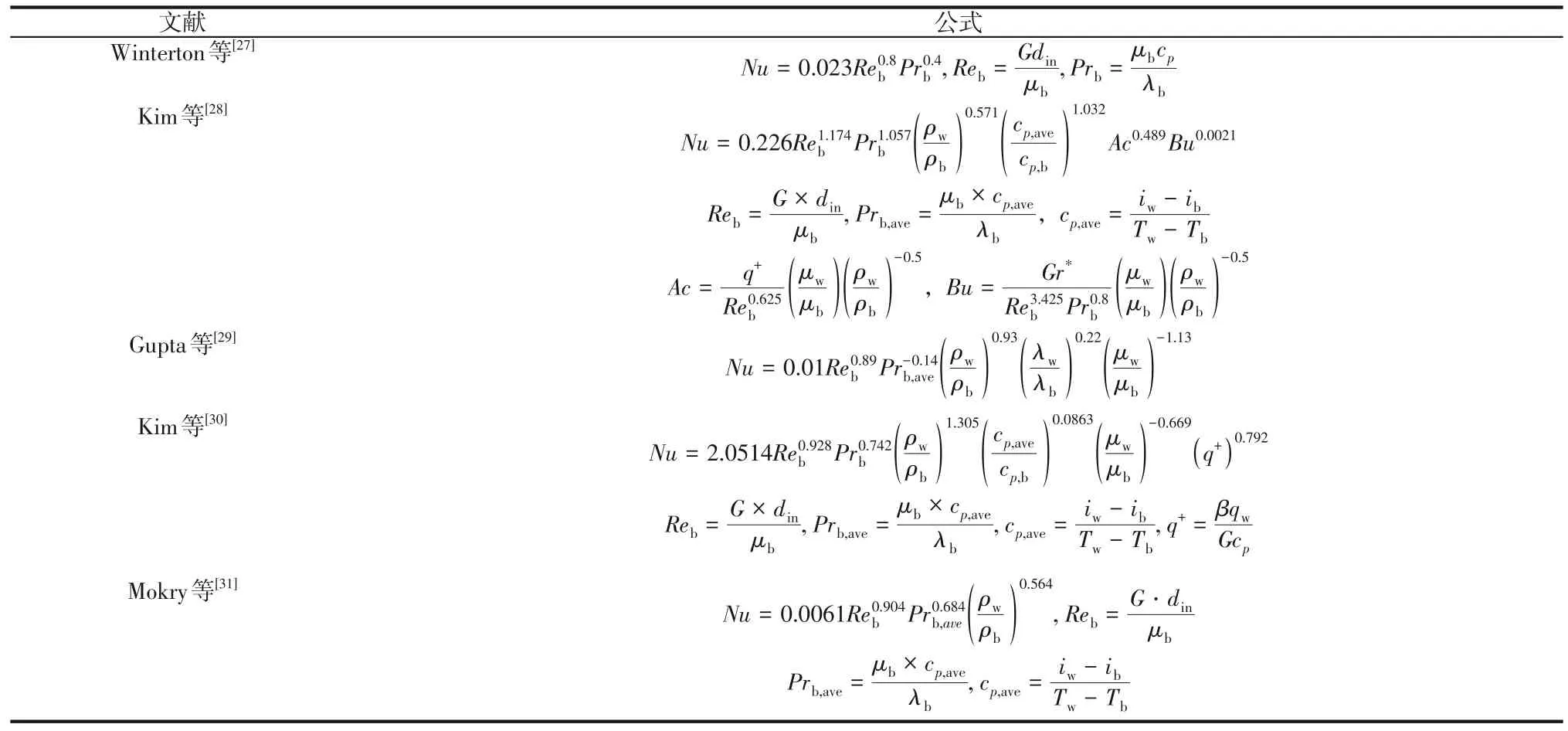
表1 超臨界傳熱關聯式

圖13 展示了已有的傳熱關聯式計算所得的努塞爾數與實驗確定的努塞爾數的分布。顯然，D-B相關的預測精度是已有五個傳熱關聯式中最差的，也說明了亞臨界壓力下的單相對流換熱的傳熱關聯式不能直接應用于超臨界流體傳熱預測。圖13(c)～(f)展示了一些研究者基于D-B 形式的傳熱關聯式，采用物性比、浮升力因子和流動加速因子對其關聯式進行了校正，提高了預測精度，但在高質量流速及惡化工況較多的條件下，精度依舊較差，在實際應用中不太能接受。而SBO 關聯式則有一個非常小的eA=0.54%，并且平均絕對誤差eR也僅為7.56%，這對于實際應用是可以接受的。與其他相關系數相比，均方根相對誤差eS也是最小的。總之，SBO關聯式給出了最好的預測精度。

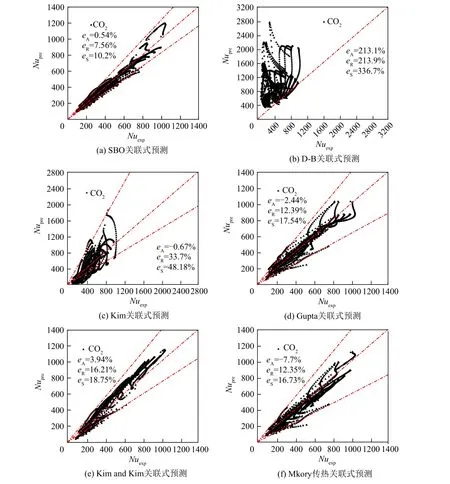
圖13 SBO關聯式和其他關聯式的比較

圖13 展示了廣泛引用的五個關聯式預測的努塞爾數Nupre與實驗確定的努塞爾數Nuexp的分布。如圖13 所示，D-B 傳熱關聯式的預測精度最差，圖13(c)～(f)展示了眾多研究者基于D-B 傳熱關聯式，采用物性比、浮升力因子和流動加速因子對其修正進而提高了預測精度。可以觀察到在高質量流速及惡化工況較多的條件下，這些關聯式精度依舊較差，在實際工程應用中不太能接受。而SBO 關聯式則有一個非常小的平均相對誤差eA=0.54%，并且平均絕對誤差eR也僅為7.56%，均方根相對誤差eS也只有10.2%，SBO 關聯式給出了最好的預測精度。

3 結論

采用SSTk-ω湍流模型研究了超臨界壓力CO2在高質量流量條件下內徑為10mm的垂直加熱管內的傳熱特性，分析討論了入口溫度、壓力、熱流密度、質量流速、浮升力和流動加速度對超臨界壓力CO2傳熱的影響。主要研究結果總結如下。

（1）通過與實驗數據的對比，發現AKN、YS、AB、LS、Standardk-ε和RNGk-ε低雷諾數湍流模型對超臨界壓力CO2傳熱的預測精度很低，SSTk-ω低雷諾數湍流模型能很好地捕捉實驗數據。表明SSTk-ω低雷諾數湍流模型對S-CO2流動換熱數值計算具有可靠的適用性。

（2）HTD 的發生與入口溫度密切相關。當入口溫度小于擬臨界溫度時HTD 發生，而當入口溫度大于擬臨界溫度時，壁面溫度單調升高；提高壓力和增大質量流速均可以延遲和抑制HTD。在高質量流速的條件下，浮升力和流動加速效應對SCO2的傳熱影響較小。從類氣膜厚度的分布角度合理地解釋了HTD發生的原因。

（3）引入超臨界沸騰數SBO，基于數值模擬及文獻數據建立超臨界壓力CO2數據庫，利用最小二乘法對各種量綱為1 的數排列組合進行選代尋優，提出了新的SBO 傳熱關聯式。與已有關聯式相比，該關聯式可以很好地預測高質量流速條件下S-CO2傳熱特性，其相對平均誤差eA、絕對誤差eR、均方根誤差eS分別為0.54%、7.56%和10.2%。