多參數(shù)優(yōu)化MPC的自動(dòng)駕駛軌跡跟蹤控制

李學(xué)慧，蘇 振，張俊友

（山東科技大學(xué)交通學(xué)院，山東 青島 266590）

0 引言

軌跡跟蹤控制是實(shí)現(xiàn)車輛自動(dòng)駕駛的關(guān)鍵技術(shù)之一［1］，其原理是將車輛當(dāng)前的實(shí)際位姿與目標(biāo)位姿進(jìn)行比較，并轉(zhuǎn)換到車身坐標(biāo)系，得到橫向誤差，通過最小化橫向誤差計(jì)算得到前輪轉(zhuǎn)角，并作用于執(zhí)行機(jī)構(gòu)，使車輛沿著目標(biāo)路徑行駛［2］。

在軌跡跟蹤控制中使用較多的控制算法有：PID控制、模型預(yù)測(cè)控制、預(yù)瞄控制和線性二次型調(diào)節(jié)器等［3］。模型預(yù)測(cè)控制能夠結(jié)合被控系統(tǒng)的動(dòng)態(tài)模型與系統(tǒng)當(dāng)前的狀態(tài)，預(yù)測(cè)系統(tǒng)未來的輸出，通過求解含約束條件的最優(yōu)控制問題，獲得系統(tǒng)的最優(yōu)控制輸入，并且具有處理多約束優(yōu)化問題的能力［4］，更適用于復(fù)雜多變的自動(dòng)駕駛應(yīng)用場(chǎng)景。車輛在高速、低附著路面和大曲率路徑工況下，傳統(tǒng)MPC算法處理能力有限，會(huì)出現(xiàn)跟蹤誤差大、穩(wěn)定性差等現(xiàn)象。近年來，通過改進(jìn)MPC算法提高自動(dòng)駕駛軌跡跟蹤精度和穩(wěn)定性成為國(guó)內(nèi)外研究熱點(diǎn)問題［5］。

改進(jìn)MPC算法主要有參數(shù)優(yōu)化和與其他算法相結(jié)合2種方式。通過參數(shù)優(yōu)化改進(jìn)的MPC算法可以不斷調(diào)整預(yù)測(cè)時(shí)域、控制時(shí)域和調(diào)整權(quán)重矩陣，從而獲得相對(duì)最優(yōu)解，更好地作用于被控系統(tǒng)。李培慶等［6］使用權(quán)重矩陣自適應(yīng)的MPC控制器，目標(biāo)函數(shù)的權(quán)重矩陣根據(jù)參考路徑的曲率變化進(jìn)行優(yōu)化調(diào)節(jié)，提高了軌跡跟蹤精度和穩(wěn)定性，但是沒有針對(duì)不同速度工況進(jìn)行優(yōu)化。李耀華等［7］建立了一種智能車軌跡跟蹤性能綜合評(píng)價(jià)指標(biāo)，制定了不同車速下的預(yù)測(cè)時(shí)域和控制時(shí)域參數(shù)調(diào)節(jié)策略，獲取最優(yōu)預(yù)測(cè)時(shí)域與控制時(shí)域，結(jié)合規(guī)劃層和控制層解決過度避障問題，減小跟蹤誤差。王銀等［8］使用自適應(yīng)軌跡跟蹤控制策略，預(yù)測(cè)時(shí)域根據(jù)車速變化進(jìn)行自適應(yīng)優(yōu)化調(diào)節(jié)，提高了低附著系數(shù)路面工況下車輛變速行駛時(shí)的軌跡跟蹤精度和穩(wěn)定性。預(yù)測(cè)時(shí)域的產(chǎn)生是通過三次多項(xiàng)式擬合4組數(shù)據(jù)得到，由于數(shù)據(jù)較少，不能得到最優(yōu)預(yù)測(cè)時(shí)域。Lin等［9］根據(jù)橫向速度和縱向速度變化，通過模糊控制調(diào)節(jié)預(yù)測(cè)時(shí)域和控制時(shí)域參數(shù)，并利用余弦相似度觸發(fā)狀態(tài)矩陣更新機(jī)制，驗(yàn)證了該策略在變速工況下具有良好的適應(yīng)性和跟蹤精度。Wang等［10］使用Mamdani模糊自適應(yīng)算法對(duì)MPC控制器權(quán)重矩陣進(jìn)行優(yōu)化調(diào)節(jié)，與傳統(tǒng)MPC算法相比，在跟蹤精度和轉(zhuǎn)向平順性方面具有更好的跟蹤性能。李韶華等［11］根據(jù)橫向誤差和橫擺角誤差使用Takagi-Sugeno模糊變權(quán)重MPC控制算法，在線優(yōu)化MPC權(quán)重矩陣，測(cè)試了該算法在不同速度下的跟蹤效果，但是沒有根據(jù)不同速度對(duì)時(shí)域進(jìn)行優(yōu)化。

在不同速度工況下，僅調(diào)節(jié)模型預(yù)測(cè)控制器的權(quán)重矩陣，能夠提高軌跡跟蹤精度，但受時(shí)域的限制，優(yōu)化幅度有限，如果在此基礎(chǔ)上同時(shí)調(diào)節(jié)時(shí)域，會(huì)進(jìn)一步提高跟蹤精度。根據(jù)車輛行駛速度、橫向位置誤差和橫擺角誤差作為模糊輸入，利用模糊控制對(duì)MPC控制器的預(yù)測(cè)時(shí)域、控制時(shí)域和權(quán)重矩陣等多個(gè)參數(shù)進(jìn)行實(shí)時(shí)優(yōu)化，通過權(quán)重矩陣優(yōu)化提高跟蹤精度，同時(shí)進(jìn)行時(shí)域優(yōu)化，進(jìn)一步提高車輛在不同速度工況下的適應(yīng)性。

1 無人車輛系統(tǒng)建模

汽車是一個(gè)復(fù)雜的非線性多約束系統(tǒng)，在研究車輛運(yùn)動(dòng)控制相關(guān)的問題時(shí)，為了降低系統(tǒng)的復(fù)雜程度，提高算法的運(yùn)算效率，在滿足車輛自身的結(jié)構(gòu)約束和控制算法需求的前提下，一般會(huì)忽略部分非研究重點(diǎn)的因素［12］，本文中假設(shè)：忽略車輛的垂向運(yùn)動(dòng)，輪胎受力的橫縱向耦合關(guān)系，載荷的左右轉(zhuǎn)移以及橫縱向空氣動(dòng)力學(xué)效應(yīng)；質(zhì)心側(cè)偏角和輪胎滑移率較小；車輛各個(gè)輪胎受力均處于線性區(qū)域。基于上述假設(shè)，將車輛簡(jiǎn)化為圖1所示的3自由度動(dòng)力學(xué)模型。

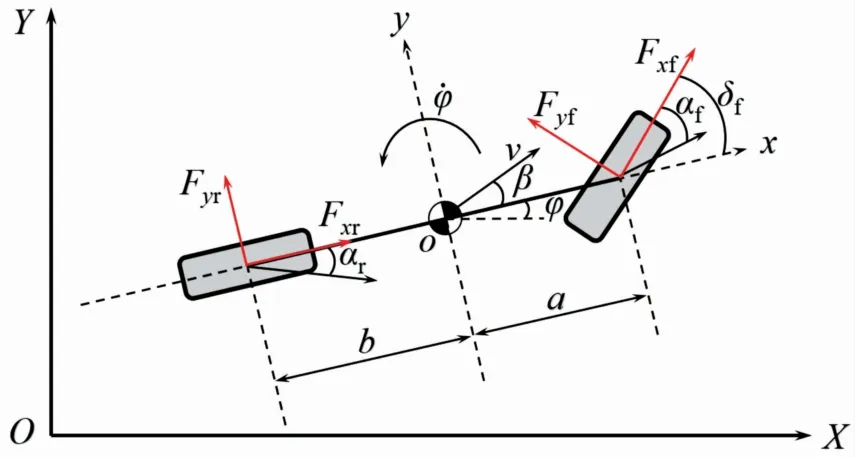
圖1 車輛3自由度模型示意圖

圖1中，a和b分別為車輛質(zhì)心與前軸和后軸的距離；v表示車輛質(zhì)心速度；φ表示車輛橫擺角；˙φ表示車輛橫擺角速度；δf表示車輛的前輪轉(zhuǎn)角；β表示質(zhì)心側(cè)偏角；x和y為車身坐標(biāo)系；X和Y表示大地坐標(biāo)系；αf和αr分別為前后輪胎側(cè)偏角；Fyf表示前輪胎側(cè)向力的合力；Fyr表示后輪胎側(cè)向力的合力；Fxf表示前輪胎縱向力的合力；Fxr表示后輪胎縱向力的合力。

簡(jiǎn)化后的車輛動(dòng)力學(xué)方程如下：

式中：m表示車輛質(zhì)量；Iz表示車輛的轉(zhuǎn)動(dòng)慣量；Clf和Clr分別表示車輛前后輪胎的縱向剛度；Ccf和Ccr分別表示車輛前后輪的側(cè)偏剛度；sf和sr分別表示前后輪滑移率。

由車身坐標(biāo)系和大地坐標(biāo)系轉(zhuǎn)換得到：

此時(shí)可以將被控系統(tǒng)描述為如下的狀態(tài)空間表達(dá)式：

2 軌跡跟蹤控制器的設(shè)計(jì)

模型預(yù)測(cè)控制屬于過程控制類策略，在每一個(gè)控制周期內(nèi)，對(duì)有限時(shí)域內(nèi)開環(huán)控制問題進(jìn)行優(yōu)化求解，并不斷地滾動(dòng)優(yōu)化實(shí)現(xiàn)反饋控制。將車輛非線性動(dòng)力學(xué)模型線性化，然后離散化，并加入約束條件，轉(zhuǎn)化為二次規(guī)劃問題求解。

2.1 非線性系統(tǒng)線性化與離散化

對(duì)系統(tǒng)的狀態(tài)方程＝f（ξ，u）在參考值ξ＝ξ0，u＝u0處利用泰勒展開式，對(duì)車輛非線性動(dòng)力學(xué)模型線性化處理后，得到線性時(shí)變方程：

再利用向前歐拉法進(jìn)行離散化后可得：

式中：Ak，t＝I＋TAt，0，Bk，t＝TBt，0，Dk，t＝TDt，0，I為單位矩陣，T為采樣周期。

令u（k）＝u（k－1）＋Δu（k），Δu（k）為控制增量，定義新的狀態(tài)變量ξ～（k）＝［ξ（k），u（k－1）］T，將式（5）轉(zhuǎn)化為以控制增量為輸入的狀態(tài)方程并生成新的狀態(tài)空間表達(dá)式：

自動(dòng)駕駛軌跡跟蹤控制的目標(biāo)是盡量減小車輛實(shí)際行駛軌跡與參考軌跡的誤差，使車輛平穩(wěn)行駛。所以目標(biāo)函數(shù)既要能表征跟蹤精度，又要能表征跟蹤穩(wěn)定性［13］。采用控制增量作為狀態(tài)量，并加入松弛因子ε，目標(biāo)函數(shù)如式（7）所示。

式中：η（·｜k）表示k時(shí)刻之后一段時(shí)間內(nèi)系統(tǒng)的輸出；ηref（·｜k）是η（·｜k）的參考值；Δu為前輪轉(zhuǎn)角增量；ρ為權(quán)重系數(shù)；ε為松弛因子；Np為預(yù)測(cè)時(shí)域，Nc為控制時(shí)域；Q和R為權(quán)重矩陣。表達(dá)式如下：

在目標(biāo)函數(shù)中還需計(jì)算控制系統(tǒng)未來時(shí)刻的輸出，系統(tǒng)的未來時(shí)刻輸出形式如下：

2.2 轉(zhuǎn)化為二次規(guī)劃問題求解

將預(yù)測(cè)模型和目標(biāo)函數(shù)相結(jié)合，構(gòu)建軌跡跟蹤二次規(guī)劃問題并設(shè)置約束條件，利用Matlab中的求解器quadprog進(jìn)行求解［14］。

式中：x表示返回值向量；H表示二次目標(biāo)矩陣，是實(shí)對(duì)稱矩陣；f表示線性目標(biāo)向量；E＝Ψkξ（k）＋ΓkΦ－Yref（k），Yref（k）是Y（k）的參考值。對(duì)式（13）進(jìn)行求解，獲得控制輸入增量序列Δ＝將該序列中第一個(gè)元素取出，當(dāng)前時(shí)刻控制量與該元素相加后作用于被控系統(tǒng)，即u（k＋1）＝u（k）＋Δ。

在設(shè)計(jì)模型預(yù)測(cè)控制器時(shí)，需要對(duì)輸出量、控制量和控制量增量進(jìn)行約束。輸出量根據(jù)車輛參考軌跡設(shè)置；對(duì)于控制量和控制量增量即車輛前輪轉(zhuǎn)角和前輪轉(zhuǎn)角增量約束可設(shè)置為：

2.3 優(yōu)化方案

將車輛行駛速度、橫向位置誤差和橫擺角誤差作為模糊輸入，利用模糊控制對(duì)MPC控制器多個(gè)參數(shù)進(jìn)行優(yōu)化，在速度不變時(shí)通過調(diào)節(jié)權(quán)重矩陣提高軌跡跟蹤精度，在不同速度工況下通過調(diào)節(jié)預(yù)測(cè)時(shí)域和控制時(shí)域?qū)刂破鬟M(jìn)一步優(yōu)化，實(shí)現(xiàn)MPC控制器多參數(shù)調(diào)節(jié)，軌跡跟蹤控制器架構(gòu)如圖2所示。

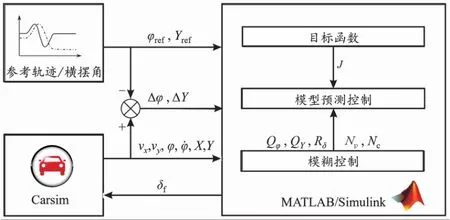
圖2 軌跡跟蹤控制器架構(gòu)

2.3.1 權(quán)重矩陣優(yōu)化

在同一速度工況下采用橫向誤差ΔY和橫擺角誤差Δφ作為Mamdani模糊控制［10］輸入，輸出權(quán)重矩陣調(diào)節(jié)系數(shù)rφ、rY和rR，通過式（15）計(jì)算改變權(quán)重矩陣Q和R，式（15）中設(shè)置初始值為：Qφ0＝200 000，QY0＝90 000，Rδ0＝500 000。Mamdani模糊控制輸入和輸出變量的隸屬度如圖3和圖4所示，Δφ的論域設(shè)置為［－15，15］，ΔY的論域設(shè)置為［－6，6］，rφ、rY和rR的論域設(shè)置為［0，1］。

圖3 輸入變量隸屬度

圖4 輸出變量隸屬度

模糊規(guī)則設(shè)置如表1—表3所示，模糊輸入輸出三維圖如圖5所示。

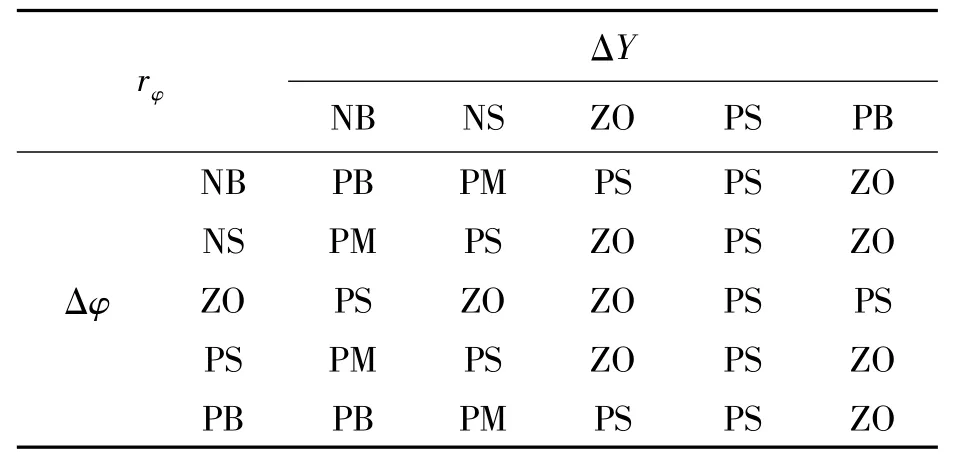
表1 rφ模糊規(guī)則

表2 rY模糊規(guī)則

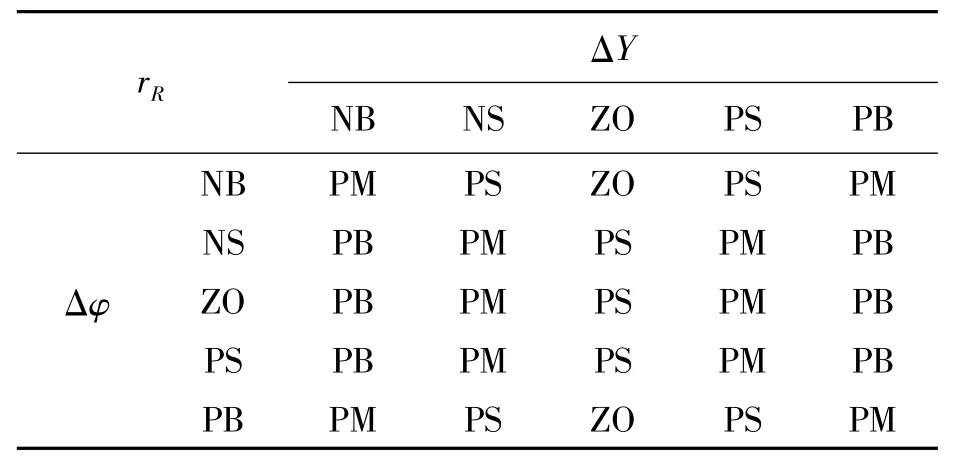
表3 rR模糊規(guī)則

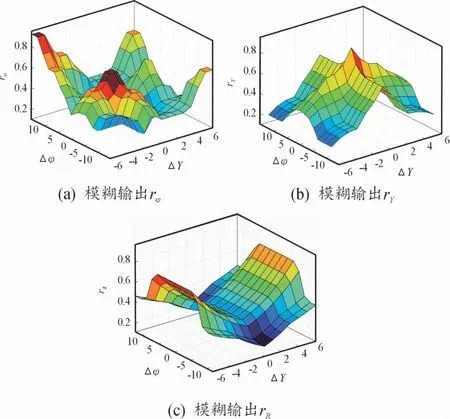
圖5 Mamdani模糊輸入輸出三維圖

2.3.2 時(shí)域優(yōu)化

MPC控制器中的預(yù)測(cè)時(shí)域與控制時(shí)域?qū)壽E跟蹤效果的影響如圖6所示。若目標(biāo)函數(shù)中其他參數(shù)不變，當(dāng)預(yù)測(cè)時(shí)域Np過大時(shí)，控制器可以預(yù)測(cè)更遠(yuǎn)的距離，會(huì)考慮到更遠(yuǎn)位置處的偏差，從而削弱對(duì)車輛當(dāng)前位置偏差的控制，導(dǎo)致過早轉(zhuǎn)向，出現(xiàn)距離車輛當(dāng)前位置較近處的跟蹤誤差較大的現(xiàn)象；當(dāng)預(yù)測(cè)時(shí)域Np過小時(shí)，預(yù)測(cè)的未來車輛狀態(tài)信息過少，車輛無法及時(shí)轉(zhuǎn)向，容易失控。當(dāng)控制時(shí)域Nc增大時(shí)，有利于控制靈敏度和精度，但會(huì)降低系統(tǒng)穩(wěn)定性和實(shí)時(shí)性；當(dāng)控制時(shí)域Nc減小時(shí)，情況則相反。

圖6 預(yù)測(cè)時(shí)域和控制時(shí)域?qū)壽E跟蹤的影響

為了使車輛在不同速度工況下控制器具有最優(yōu)時(shí)域參數(shù)，設(shè)置預(yù)測(cè)時(shí)域初始值Np0，控制時(shí)域初始值Nc0，通過Takagi－Sugeno模糊控制獲得系數(shù)rNp和rNc，使用式（16）計(jì)算Np和Nc。因?yàn)橄禂?shù)rNp和rNc的論域設(shè)置為［0，1］，Np和Nc的值不超過Np0和Nc0，所以Np0和Nc0的設(shè)置不能太小，結(jié)合相關(guān)文獻(xiàn)，并反復(fù)仿真實(shí)驗(yàn)后選取Np0＝33、Nc0＝16。

Takagi-Sugeno模糊控制的輸入為速度v，輸出為系數(shù)rNp和rNc，速度v論域設(shè)置為［0，12］，速度v論域與真實(shí)車速v*的數(shù)量關(guān)系為v＝v*／10，v*單位為km／h，速度v隸屬度如圖7所示。T-S模糊規(guī)則如表4所示，時(shí)域調(diào)節(jié)模糊規(guī)則二維關(guān)系如圖8所示。

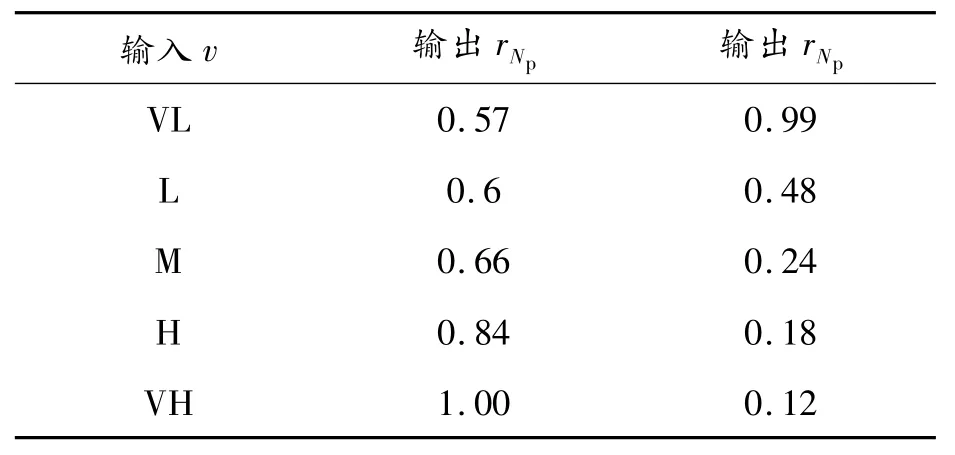
表4 時(shí)域調(diào)節(jié)模糊規(guī)則

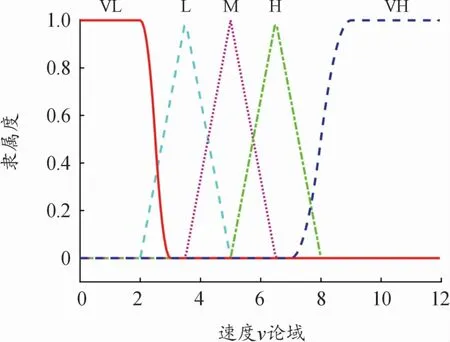
圖7 速度隸屬度

圖8 Takagi-Sugeno模糊輸出二維圖

3 仿真驗(yàn)證

在自動(dòng)駕駛車輛行駛過程中，需要將可行性、安全性和穩(wěn)定性作為優(yōu)化目標(biāo)。可行性表現(xiàn)為車輛前輪轉(zhuǎn)角控制在規(guī)定范圍，安全性表現(xiàn)為車輛行駛過程中軌跡跟蹤精度，穩(wěn)定性表現(xiàn)為車輛行駛過程中橫擺角誤差的變化。為了檢驗(yàn)改進(jìn)的MPC控制器的跟蹤效果，使用Matlab和Carsim進(jìn)行軌跡跟蹤控制聯(lián)合仿真，在Matlab中搭建MPC控制器，輸出控制量作用于Carsim，Carsim將車輛實(shí)時(shí)狀態(tài)變量輸出作用于Matlab。

3.1 工況選擇

參考軌跡選擇雙移線方程，路徑設(shè)置如下：

式中：Yref為橫向參考坐標(biāo)；φref為參考橫擺角；Xref為參考縱向坐標(biāo)；dx1、dx2、dy1、dy2均為軌跡參數(shù)。

3.2 仿真參數(shù)設(shè)置

MPC傳統(tǒng)算法使用如表5所示的5個(gè)固定參數(shù)，MPC多參數(shù)調(diào)節(jié)算法對(duì)這5個(gè)參數(shù)進(jìn)行實(shí)時(shí)優(yōu)化，MPC僅時(shí)域調(diào)節(jié)算法只優(yōu)化Np和Nc，MPC僅權(quán)重調(diào)節(jié)算法只優(yōu)化Qφ、QY和Rδ。Carsim中均使用B-Class車型，車輛參數(shù)如表6所示。

表5 模型預(yù)測(cè)控制器參數(shù)

表6 車輛主要參數(shù)

3.3 仿真結(jié)果評(píng)價(jià)

在高附著系數(shù)μ＝0.8的路面上進(jìn)行36、54、72 km／h三種典型車速仿真實(shí)驗(yàn)；在低附著系數(shù)μ＝0.4的路面進(jìn)行54 km／h車速仿真實(shí)驗(yàn)。將使用改進(jìn)MPC控制器的車輛與傳統(tǒng)MPC控制器的車輛進(jìn)行仿真對(duì)比。

3.3.1 高附著路面仿真分析

1）橫向誤差對(duì)比。不同車速下軌跡如圖9所示，在X＝53 m和85 m附近大曲率路徑處，采用MPC多參數(shù)優(yōu)化算法的控制器具有更高的跟蹤精度，采用其余3種算法的控制器都由于過早轉(zhuǎn)向?qū)е赂櫿`差較大。為了更清晰地觀察橫向軌跡誤差大小的變化，設(shè)置ΔY＝Y(jié)ref－Y，如圖10所示，可以直觀地顯示橫向誤差的變化。

圖9 不同車速下軌跡曲線

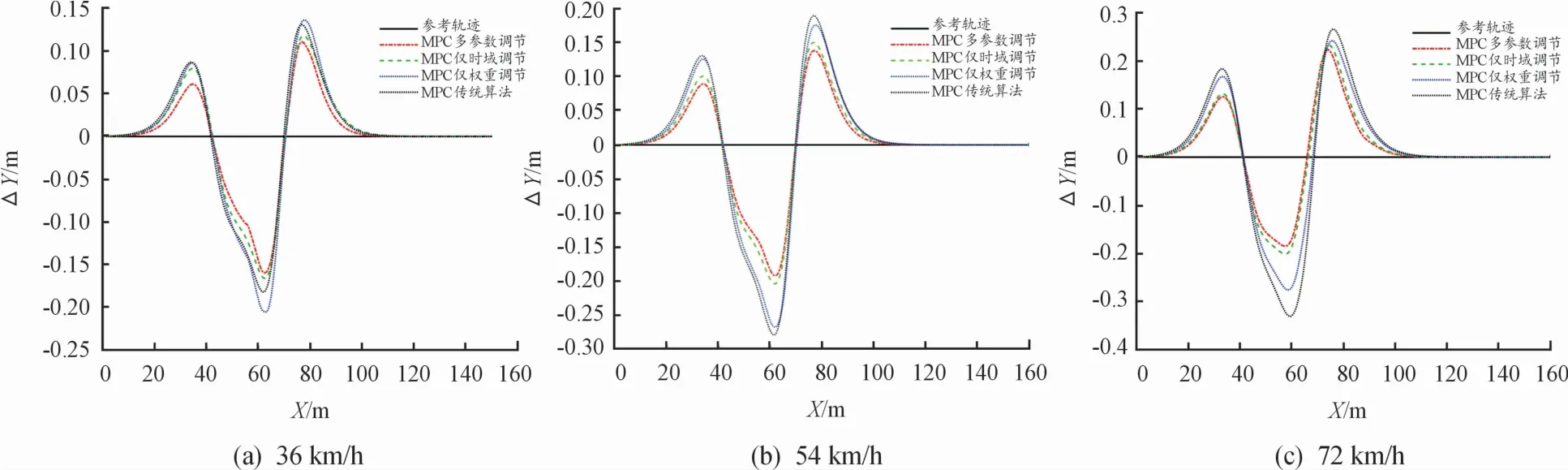
圖10 橫向誤差變化曲線

在測(cè)試的速度工況下，隨著速度提高，采用MPC多參數(shù)優(yōu)化算法的控制器在減小橫向誤差方面優(yōu)于采用MPC僅時(shí)域調(diào)節(jié)和僅權(quán)重調(diào)節(jié)的控制器，特別是在72 km／h工況下，MPC多參數(shù)優(yōu)化算法優(yōu)勢(shì)更加明顯。

對(duì)橫向誤差仿真結(jié)果進(jìn)行數(shù)據(jù)統(tǒng)計(jì)，統(tǒng)計(jì)結(jié)果如表7所示，數(shù)據(jù)表明：在減小橫向誤差方面，不同速度工況下，采用MPC多參數(shù)優(yōu)化算法的控制器均表現(xiàn)最優(yōu)，平均優(yōu)化比例可達(dá)27.4%。

表7 最大橫向誤差

2）橫擺角誤差對(duì)比。橫擺角誤差可以反映車輛行駛的穩(wěn)定性，為了清晰地觀察橫擺角誤差大小及誤差變化，設(shè)置Δφ＝φref－φ，橫擺角誤差變化如圖11所示。在低速36 km／h時(shí)，4種控制器的橫擺角誤差變化區(qū)別不明顯；在54 km／h時(shí)，采用MPC多參數(shù)優(yōu)化算法控制器的車輛行駛過程中橫擺角誤差較小；在72 km／h時(shí)，4種MPC控制器的車輛橫擺角誤差曲線都出現(xiàn)明顯波動(dòng)，采用MPC多參數(shù)優(yōu)化算法控制器的車輛行駛過程中橫擺角波動(dòng)幅度較小。

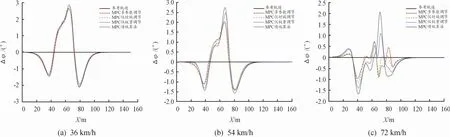
圖11 橫擺角誤差變化

對(duì)橫擺角誤差仿真結(jié)果進(jìn)行數(shù)據(jù)統(tǒng)計(jì)，統(tǒng)計(jì)結(jié)果如表8所示，在減小最大橫擺角誤差方面，3種改進(jìn)算法都比傳統(tǒng)算法有優(yōu)勢(shì)，采用MPC多參數(shù)優(yōu)化算法的控制器在減小最大橫擺角誤差方面表現(xiàn)最優(yōu)，車輛行駛穩(wěn)定性最好，特別是72 km／h的時(shí)候，最大橫擺角誤差優(yōu)化明顯，誤差在1°以內(nèi)。

表8 最大橫擺角誤差

3）歐氏距離對(duì)比。為了能夠評(píng)價(jià)軌跡跟蹤全過程的整體誤差，基于歐式距離的相似度算法［15］對(duì)采用不同MPC控制器的車輛實(shí)際行駛軌跡與參考軌跡進(jìn)行對(duì)比。歐式距離模型如圖12所示，計(jì)算Ni和Mi兩點(diǎn)間的歐氏距離：

圖12 歐式距離模型

實(shí)際軌跡與參考軌跡的歐式距離可表示為：

歐氏距離綜合考慮軌跡的整體誤差，用于評(píng)價(jià)跟蹤效果更準(zhǔn)確，車輛在雙移線路徑行駛時(shí)，跟蹤誤差主要分布在縱向位移0～100 m處，在此范圍內(nèi)均勻取點(diǎn)100個(gè)，即式（19）中n＝100。對(duì)歐氏距離計(jì)算結(jié)果進(jìn)行數(shù)據(jù)統(tǒng)計(jì)，統(tǒng)計(jì)結(jié)果如表9所示，數(shù)據(jù)表明：采用MPC多參數(shù)優(yōu)化算法控制器的歐氏距離明顯低于其余3種控制器，平均優(yōu)化比例可達(dá)16.5%。

表9 歐氏距離

3.3.2 低附著路面仿真分析

為了驗(yàn)證多參數(shù)優(yōu)化MPC控制器在低附著路面工況下的優(yōu)勢(shì)，選取附著系數(shù)μ＝0.4，車速為54 km／h進(jìn)行仿真實(shí)驗(yàn)。低附著路面仿真結(jié)果如圖13所示，將仿真結(jié)果進(jìn)行數(shù)據(jù)統(tǒng)計(jì)，統(tǒng)計(jì)結(jié)果如表10—表12所示。仿真結(jié)果表明：與其余3種控制算法相比，采用MPC多參數(shù)優(yōu)化算法控制器的車輛行駛軌跡更接近參考軌跡，且橫擺角誤差波動(dòng)較小，在低附著路面工況下具有良好的操縱穩(wěn)定性；采用僅時(shí)域優(yōu)化算法的MPC控制器由于過度減小最大橫向誤差，導(dǎo)致軌跡在X＝85 m附近出現(xiàn)明顯波動(dòng)，且橫擺角誤差在X＝90 m附近出現(xiàn)明顯波動(dòng)，操縱穩(wěn)定性較差。采用MPC多參數(shù)優(yōu)化算法控制器的車輛行駛軌跡具有更小的歐氏距離，軌跡跟蹤整體誤差減小。

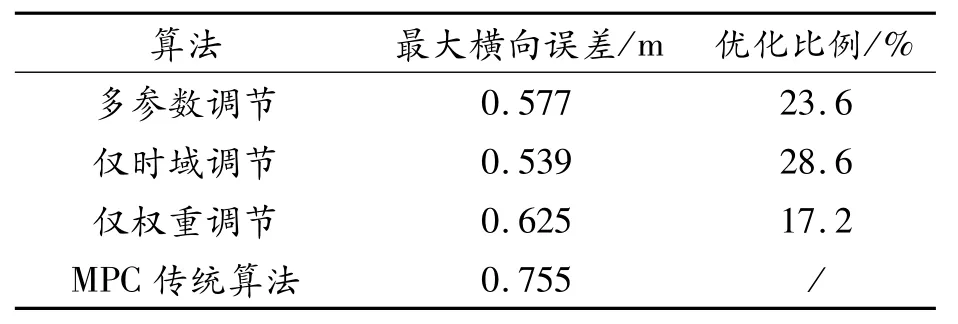
表10 最大橫向誤差

表11 最大橫擺角誤差

表12 歐氏距離

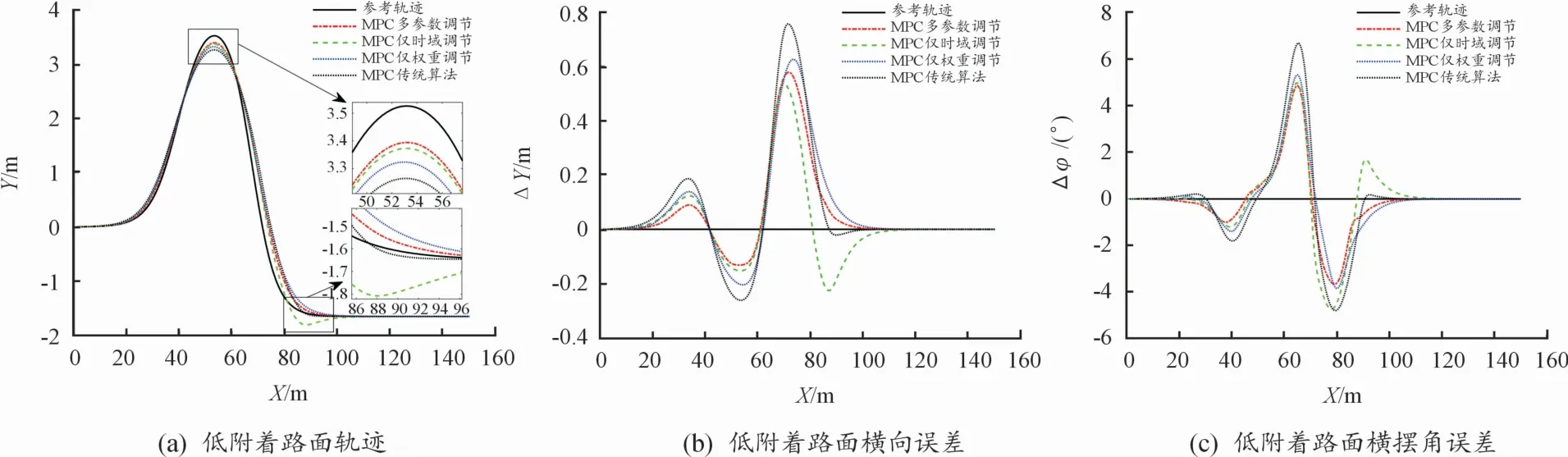
圖13 低附著路面仿真結(jié)果

4 結(jié)論

1）針對(duì)自動(dòng)駕駛車輛橫向控制在大曲率路徑處跟蹤誤差較大的問題，提出了多參數(shù)優(yōu)化MPC的自動(dòng)駕駛軌跡跟蹤控制策略，進(jìn)行了仿真驗(yàn)證。

2）采用MPC多參數(shù)優(yōu)化算法的控制器在高附著路面，能夠更好地減小最大橫向誤差，提高跟蹤精度，保持良好的操縱穩(wěn)定性，在車速72 km／h雙移線工況下將最大橫擺角誤差控制在1°以內(nèi)。

3）采用MPC多參數(shù)優(yōu)化算法的控制器在低附著路面，能夠更好地平衡跟蹤精度與操縱穩(wěn)定性，避免因提高跟蹤精度而降低操縱穩(wěn)定性，在車速為54 km／h工況下，比MPC傳統(tǒng)算法的最大橫擺角誤差減小27.3%。