涂層鋯合金包殼管切向微動磨損數(shù)值預測模型研究

王凱模，沈火明，王宇星，2，廖業(yè)宏，劉 娟，任啟森，彭振馴，黃 恒

（1.西南交通大學力學與航空航天學院，成都 610031；2.西南交通大學機械工程學院，成都 610031；3.中廣核研究院有限公司核燃料與材料研究所，廣東 深圳 518026）

0 引言

核燃料包殼作為核反應堆安全的首道屏障，能夠防止核裂變產物的泄漏，其完整性是決定反應堆正常、高效運行的關鍵。而反應堆中冷卻水自下而上的流動會導致核燃料包殼與其支撐格架之間發(fā)生嚴重的微動磨損［1］，引起核燃料組件的破壞及失效，嚴重時甚至會造成核裂變產物的泄漏。因此，研究包殼-格架的微動磨損行為對于保障核反應堆壽命是至關重要的。

研究人員對包殼微動磨損行為開展了大量研究工作。鄧星［2］研究在球-平面接觸下，交變載荷條件下Zr-4合金的切向微動磨損特性，發(fā)現(xiàn)磨損體積和磨損深度隨著位移幅值增加而增加。趙杰江等［3］通過二維柱面-平面有限元模型模擬了鋯合金切向微動磨損試驗，結果表明在整體滑移狀態(tài)下，鋯合金磨損速率隨位移幅值增加而增加，隨法向力增加先增加后減小。在部分滑移狀態(tài)下，磨損率隨位移幅值的增加增長緩慢，隨法向力增加緩慢減小。高雯［4］對包殼磨損的摩擦因數(shù)進行了研究，發(fā)現(xiàn)摩擦因數(shù)隨載荷的增加呈線性增加趨勢。Attia［5］研究了鋯合金在高溫下的微動磨損行為，發(fā)現(xiàn)鋯合金的磨損率隨功率的增加而減小。齊歡歡等［6］采用Archard模型［7］預測了燃料棒包殼與格架之間的微動磨損，發(fā)現(xiàn)磨損預測需要確定磨損系數(shù)、接觸力和滑動距離3個參數(shù)。唐力晨等［8］建立了鋯合金管-格架彈簧微動磨損的計算分析模型，發(fā)現(xiàn)磨損量和最大磨損深度隨磨損周次的計算結果與試驗結果符合較好。近年來，法國原子能協(xié)會、法瑪通等機構對涂層鋯合金的微動磨損行為進行了研究，研究均表明涂層鋯合金能顯著降低包殼的磨損程度［9－10］。綜上所述，目前研究主要針對鋯合金包殼的微動磨損，針對鉻涂層鋯合金包殼［11］的微動磨損研究較少，同時缺少對包殼-格架實際幾何特征的考慮。

本研究考慮包殼-剛凸的幾何特征，建立對應的有限元模型，基于Archard磨損計算模型在ABAQUS中結合ALE自適應功能實現(xiàn)磨損仿真。通過涂層鋯合金管-剛凸切向微動磨損試驗獲得摩擦因數(shù)、磨損系數(shù)的試驗數(shù)據(jù)，同時考慮磨損系數(shù)隨磨損周次的變化情況，最后得到涂層鋯合金管-剛凸切向微動磨損的有限元計算模型。本文中建立的模型可較好地預測涂層包殼管-剛凸的最大磨損深度，對包殼-格架系統(tǒng)的磨損預測具有參考意義。

1 有限元模型

為研究包殼管-剛凸的切向磨損行為，根據(jù)包殼管和剛凸的幾何尺寸，同時參照切向磨損試驗中包殼管-剛凸的約束形式，建立如圖1所示的包殼-剛凸三維有限元模型。截面尺寸如圖2所示，剛凸沿Z方向寬度為3.3 mm，包殼管沿Z方向寬度取6 mm。

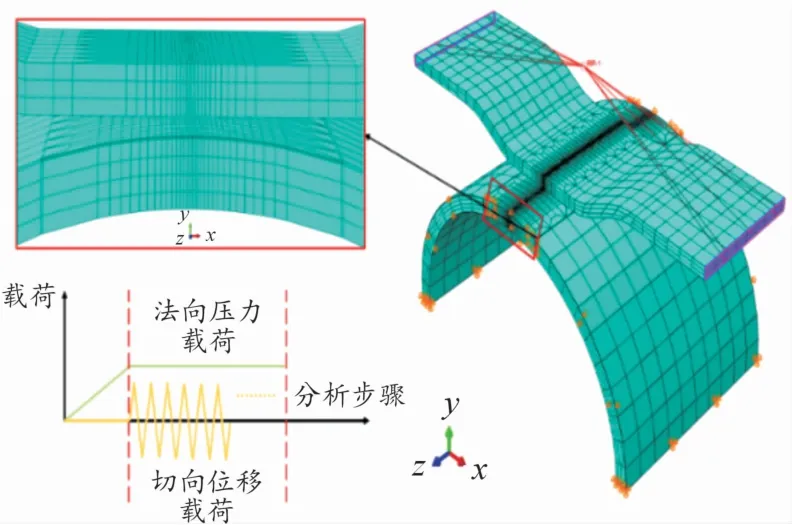
圖1 包殼-剛凸有限元模型／加載方式

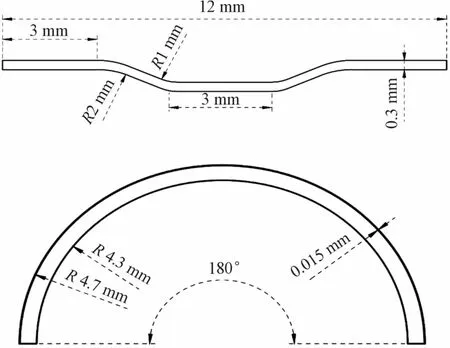
圖2 截面尺寸示意圖

同時考慮模型計算效率和計算精度，對模型接觸區(qū)域進行局部網格加密，剛凸的最小網格尺寸為16μm×75μm×173.5μm，包殼管的最小網格尺寸為13μm×5μm×200μm，單元類型為C3D8R。接觸設置為面-面接觸，包殼管表面設置為主面，剛凸表面設置為從面，切向設置為具有各向同性摩擦的庫侖摩擦定律，摩擦因數(shù)為0.6；法向設置為硬接觸，采用有限滑移算法，切向約束設置為“罰”。

包殼軸向截面采用鉸接約束，周向截面僅約束Z方向，剛凸的運動通過控制與端面耦合的參考點RP-1實現(xiàn)。切向磨損仿真加載過程包含2個分析步，如圖1所示。第1個分析步僅保留參考點Y方向的自由度，同時施加法向的壓力載荷；第2個分析步保持壓力載荷恒定的同時施加切向周期變化的位移載荷。

剛凸以及包殼基體材料為鋯合金，彈性模量為95.6 GPa，泊松比為0.332 5；涂層材料為鉻，彈性模量為258.9 GPa，泊松比為0.22。

磨損過程通常可分為3個階段。首先是跑合磨損階段：新的摩擦副在運行初期，由于對偶表面的表面粗糙度值較大，實際接觸面積較小，接觸點數(shù)少而多數(shù)接觸點的面積又較大，接觸點粘著嚴重，因此磨損系數(shù)較大；其次是穩(wěn)定磨損階段：這一階段磨損緩慢且穩(wěn)定，磨損系數(shù)保持基本不變；最后是劇烈磨損階段：經過長時間的穩(wěn)定磨損后，由于摩擦副對偶表面間的間隙和表面形貌的改變以及表層的疲勞，其磨損系數(shù)急劇增大。本文中主要研究包殼管-剛凸失效前的磨損行為，故僅考慮前2個磨損階段磨損系數(shù)的變化情況。

通過已開展的試驗發(fā)現(xiàn)，當磨損周次達到30萬周次時，磨損進入穩(wěn)定磨損階段。通過試驗數(shù)據(jù)擬合得到包殼管-剛凸切向磨損系數(shù)與磨損周次的關系式如下：

式中：k為磨損系數(shù)；為前30萬周次的平均磨損系數(shù)，通過試驗得到；N為磨損周次（萬次）。

2 磨損有限元實現(xiàn)

在進行微動磨損的有限元仿真時，需要對接觸面節(jié)點坐標進行控制以保證磨損表面符合實際情況，故采用一種適用于微動磨損的磨損模型來計算每次的磨損量。選擇合適的磨損模型是微動磨損仿真的關鍵，通常有2種磨損模型用來預測磨損過程，即Archard模型和能量模型。當接觸面間的摩擦因數(shù)不是定值或者當接觸面間產生部分滑移時，Archard模型很難對微動磨損進行合理的定量計算。能量模型的優(yōu)點在于其磨損系數(shù)不受位移幅值以及摩擦因數(shù)大小的影響，測量更加準確。但由于需要獲得大量的摩擦切應力-滑移量數(shù)據(jù)，且要求相當大的采樣密度，再通過積分獲得能耗值，這種方法很難實現(xiàn)，應用偏少。

選取Archard模型作為磨損計算模型。其磨損深度的計算式如下：

式中：h（x）為位置x處的磨損深度；ΔN為加速次數(shù)；k為磨損系數(shù)；p（x）i表示位置x處第i增量步的局部接觸壓力；Δs（x）i表示位置x處第i增量步的局部相對滑移增量。

通過ABAQUS主程序計算可以得到局部接觸壓力和局部相對滑移量，通過變量CPRESS和CSLIP傳遞給UMESHMOTION子程序。子程序根據(jù)加速次數(shù)以及磨損系數(shù)計算出對應的局部磨損深度并將值返回給ABAQUS主程序。結合ALE自適應網格技術更新輪廓，微動磨損仿真流程如圖3所示。

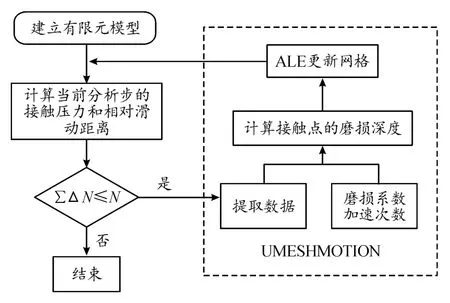
圖3 微動磨損仿真流程

3 模型驗證

核電領域通常規(guī)定，當包殼管磨損深度達到壁厚的10%時即認為已失效，所以包殼管-剛凸切向微動磨損研究主要關注最大磨損深度。有限元計算結果與試驗結果見圖4所示。有限元計算結果與試驗結果吻合較好，說明本文中建立的有限元計算模型在一定程度上能夠表征包殼管-剛凸切向微動磨損行為。

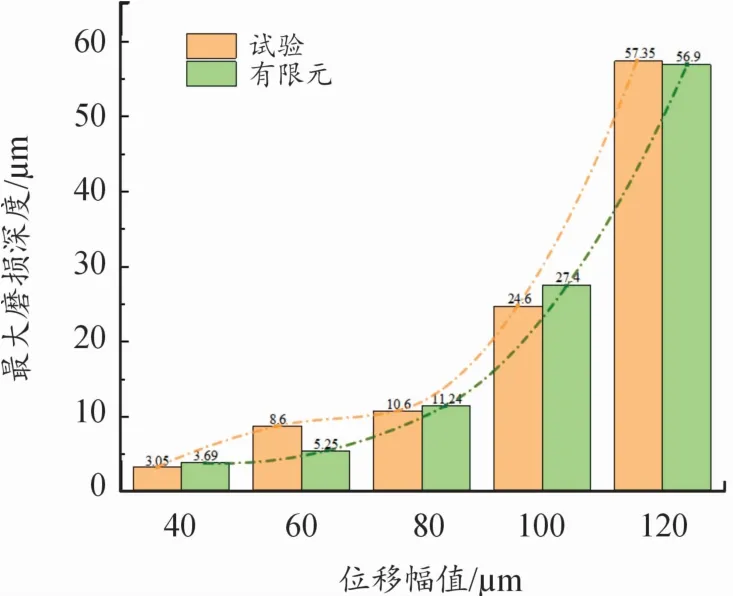
圖4 試驗／有限元最大磨損深度

4 磨損結果分析

4.1 F-D曲線

摩擦力-位移曲線（F-D曲線）是微動磨損中最基本的信息，曲線形狀可以用來描述接觸面間的相對運動關系。如圖5所示，法向預緊力為50 N，位移幅值為40、60、80μm時F-D曲線為橢圓形，如圖5（a）所示，此時微動運行處于部分滑移狀態(tài)，且隨著位移幅值的增大滑移區(qū)逐漸增大；當位移幅值為100、120μm時F-D曲線為平行四邊形，如圖5（b）所示，此時微動運行處于完全滑移狀態(tài)。

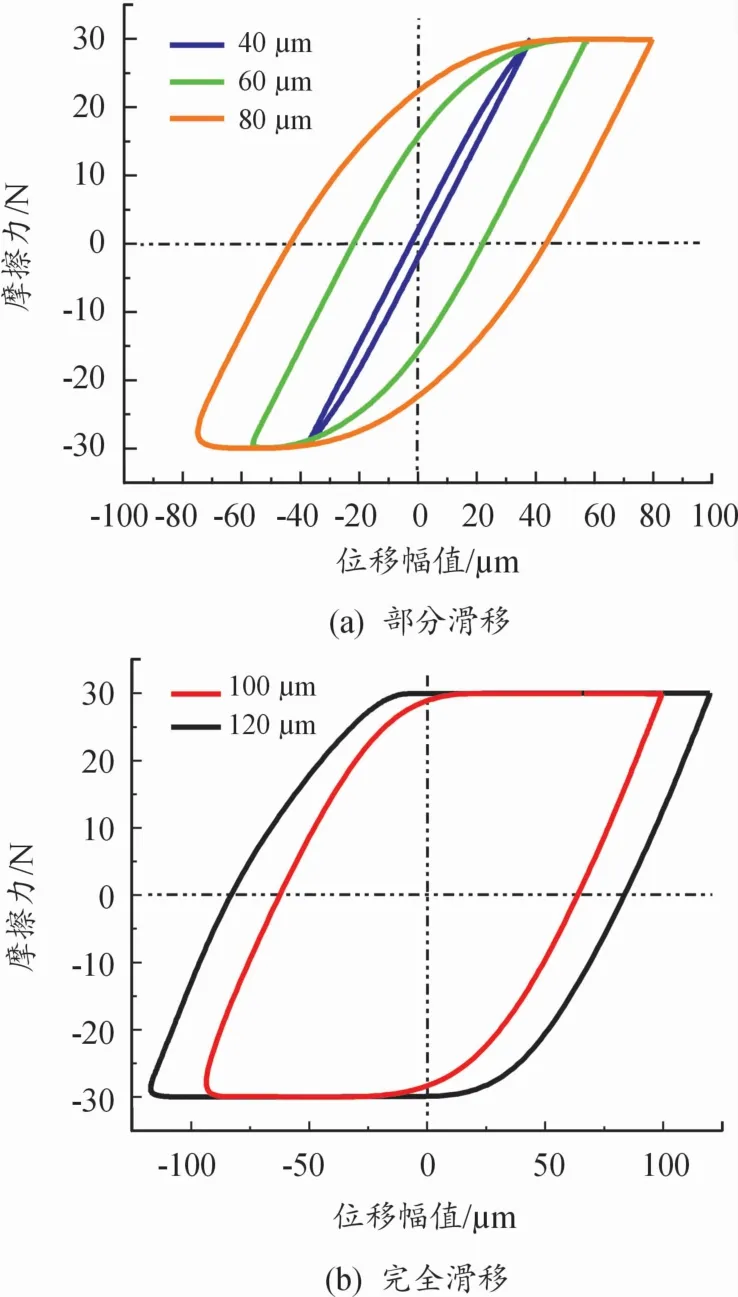
圖5 F-D曲線

4.2 磨損輪廓

預緊力50 N、磨損2萬周次時，不同位移幅值的磨損輪廓如圖6所示。位移幅值越大，磨損寬度和深度越大。

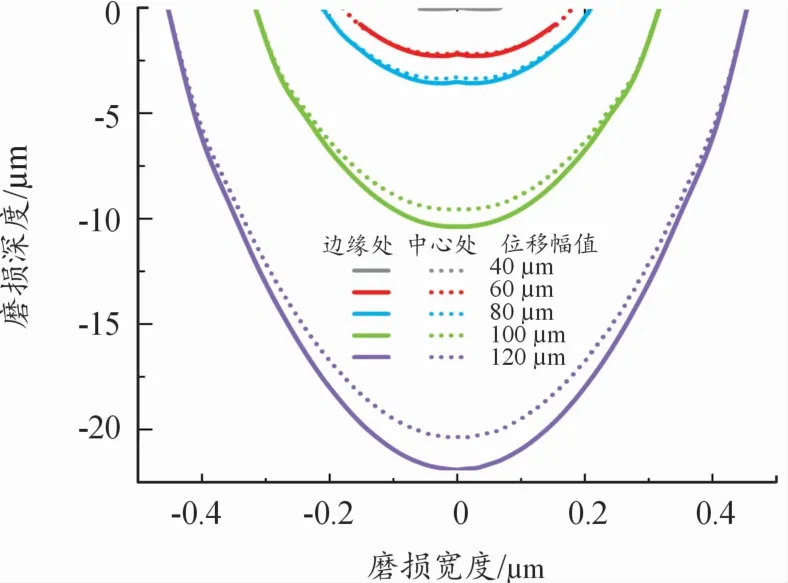
圖6 磨損輪廓示意圖

沿軸向方向接觸壓力不是均勻分布的，不同預緊力載荷作用下沿軸線方向的接觸壓力分布如圖7所示，接觸邊緣處的接觸壓力均大于接觸中心處，所以沿軸線方向（Z方向）包殼-剛凸接觸邊緣的磨損深度均大于接觸中心處。

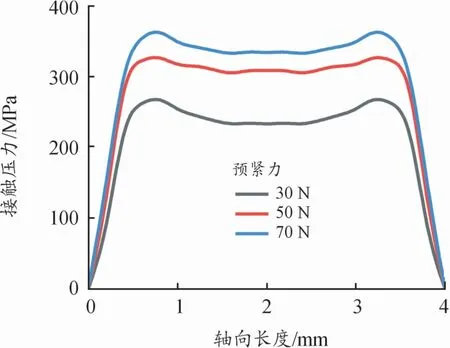
圖7 接觸壓力分布

4.3 最大磨損深度

不同位移幅值、不同預緊力、磨損周次為5萬次下有限元計算的最大磨損深度如圖8所示。在部分滑移和完全滑移狀態(tài)下，預緊力越大，位移幅值越大，對應的最大磨損深度越大；完全滑移狀態(tài)下的最大磨損深度顯著大于部分滑移狀態(tài)下的最大磨損深度。

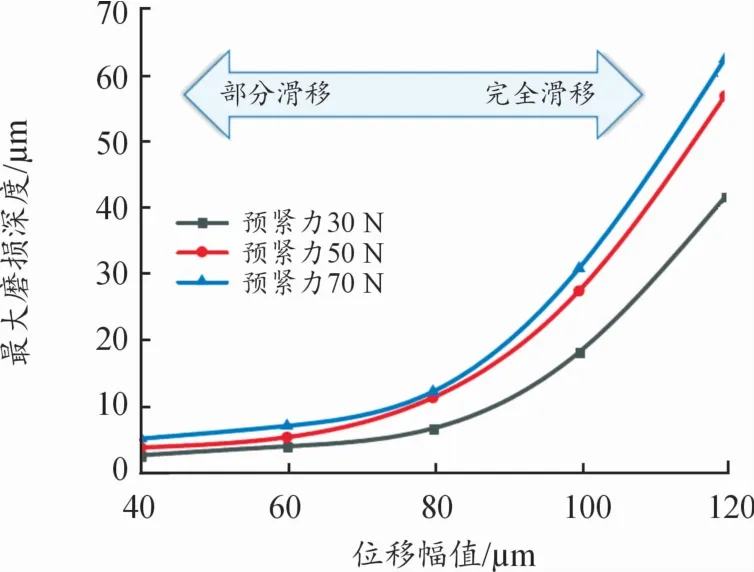
圖8 最大磨損深度（5萬磨損周次）

預緊力為50 N、不同位移幅值以及不同磨損周次下有限元計算的最大磨損深度如圖9所示。相同預緊力、位移幅值作用下，磨損周次越大，最大磨損深度越大；隨著磨損周次增加，磨損速率逐漸減小后趨于平緩，且位移幅值越大，磨損穩(wěn)定階段的磨損速率越大。

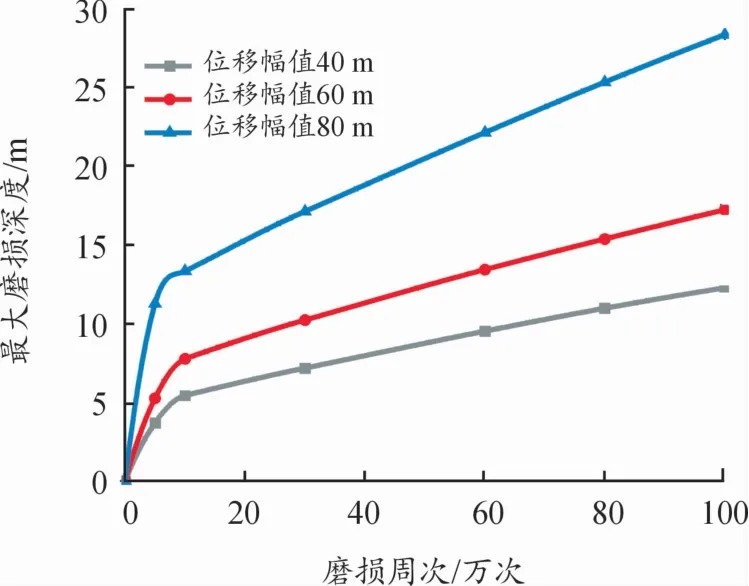
圖9 最大磨損深度（50 N預緊力）

5 結論

1）法向預緊力為50 N，位移幅值為40、60、80 μm時微動運行處于部分滑移狀態(tài)，當位移幅值為100、120μm時微動運行處于完全滑移狀態(tài)。

2）沿軸線方向（Z方向）包殼-剛凸接觸邊緣的磨損深度均大于接觸中心處，因為接觸中心為面接觸，而接觸邊緣為線接觸，其接觸應力更大。

3）在部分滑移和完全滑移狀態(tài)下，預緊力越大，其接觸壓力越大，位移幅值越大，相對滑移距離越大，對應的最大磨損深度越大；完全滑移狀態(tài)下的最大磨損深度顯著大于部分滑移狀態(tài)下的最大磨損深度。

4）相同工況下磨損速率隨著磨損周次逐漸減小并趨于穩(wěn)定，相同預緊力下，位移幅值越大，其穩(wěn)定磨損階段的磨損速率越大。