基于混合稀疏ICCP 的聯合抗差重力匹配定位方法

丁繼成，杜翔宇，楊崇昭，趙 巖

（哈爾濱工程大學 智能科學與工程學院，哈爾濱 150001）

重力場信息具有良好的時空分布特征，利用重力場信息與重力場數據庫進行匹配來獲得導航定位信息具有自主性和隱蔽性，且定位誤差不隨時間而累積，經常用于輔助慣性導航系統（Inertial Navigation System,INS），來實現長時間航行并保持高精度導航定位。使用重力導航系統輔助慣導系統進行誤差校正，既能獲得高精度導航定位結果，同時也不會破壞導航系統的自主性[1,2]。

匹配算法是重力匹配導航系統的核心部分，經典的算法有地形輪廓匹配（Terrain Contour Matching,TERCOM）算法、最近等值線迭代（Iterative Closest Contour Point,ICCP）算法、桑地亞慣性地形輔助導航（Sandia Inertia Terrain-aided Navigation,SITAN）算法[3,4]。其中TERCOM 算法對于航向誤差較為敏感，SITAN 算法對初始位置的精度要求較高。而ICCP 算法最初來源于點云配準的迭代最近點（Iterative Closest Point,ICP）算法，具有精度高，易于實現等特點。其主要思想是通過迭代最近等值線點來實現測量與基準圖之間的匹配。該算法先利用慣性導航系統的指示位置，尋找重力圖中相應的搜索域，并搜索其最近等值線點，然后以歐氏距離平方和最小的原則不斷進行剛性變換，通過重復變換逐步靠近真實航跡，從而對慣導系統的誤差進行修正[5]。

ICCP 算法成立是建立在兩個假設基礎上的：(1)INS 提供的指示航跡接近真實軌跡，且累積誤差不大；(2) 重力傳感器無測量誤差。假設(1)可以通過不斷使用ICCP 算法提供充足的外部信息來限制INS 誤差的積累，而假設(2)在實際應用中無法實現，不論是重力基準圖的預測量還是航行中重力傳感器的實際測量，測量誤差都不可避免且不可能完全一致，因此會造成最近等值線點不一定存在或者不能確定的情況，導致匹配算法失配或誤配[6]。針對于實際測量中重力傳感器不可避免存在噪聲的問題，國內學者對此進行了深入的研究。從噪聲統計特性方面考慮，肖晶等提出了一種基于概率數據關聯的地磁ICCP 算法，對某一位置的地磁場進行多次測量，并根據概率數據關聯的思想，融合測量值對應的結果，提升了匹配算法的定位精度和魯棒性[7]；陳卓等提出了一種基于可信點集和軌跡的搜索方法來拒絕標量匹配的不可靠迭代點，提高了匹配的準確性[8]；許寧徽等提出一種基于多屬性決策的評價指標，通過熵權法將收斂度指標與軌跡相關性指標融合得到綜合評價指標，在噪聲干擾的情況下也能很好地收斂[9]。從濾波角度考慮，喬楠等提出了一種基于多尺度特征值經驗模態分解的地磁濾波方法，通過濾除干擾信號和重構信號來抑制測量噪聲[10]。以上文獻對抑制ICCP 算法測量噪聲影響方面進行了不同程度的改進，但均未考慮測量誤差對ICCP 算法匹配殘差的影響。

針對重力傳感器存在測量誤差導致傳統ICCP 算法誤配或失配的問題，本文首先對ICCP 算法的匹配殘差進行分析，仿真驗證匹配殘差在高斯噪聲影響下不服從高斯分布，進而利用解決稀疏性問題的非凸lp范數優化模型，研究構造增廣拉格朗日函數，基于lp范數對ICCP 算法進行改進，使用了加權的混合正則項，以更泛化地表示匹配殘差，對最近等值線點進行重調。最后，構建聯合匹配算法，使用混合稀疏ICCP（Hybrid Sparse ICCP,HS-ICCP）算法進行粗匹配，提供有效的匹配區域，將匹配后的位置作為新的INS 指示位置提供給經典ICCP 算法進行精匹配，有效地減少了重力傳感器測量誤差對匹配結果的影響。

1 ICCP 算法分析

1.1 ICCP 算法原理

ICCP 算法是ICP 算法以等值線為匹配單元的特例，它不需要對環境進行事先估計分析，只需要不斷重復迭代計算，直至達到迭代的終止條件，將匹配結果作為對真實航跡的估計，從而修正INS 誤差[11]。

ICCP 算法原理圖如圖1 所示，當航行器進入匹配區域后，利用重力傳感器測量并記錄航行軌跡點的重力異常值。根據INS 系統提供的位置信息，提取對應區域的重力異常數據庫，再根據實測重力異常值gi(i=1,2...N)，在重力異常數據庫中提取INS 指示航跡 點xi(i=1,2...N)附近的重力異常等值線ci(i=1,2...N)，并在等值線ci上搜索到與點xi距離最近的點yi(i=1,2...N)，然后以INS 指示點集和最近等值線點集間的歐式距離最小為目標函數，求解對應的旋轉矩陣和平移矢量，并對INS 指示航跡點集應用求解的剛性變換，不斷重復迭代這一過程，直至收斂[12]。這實際上是一種求解最優化問題的過程，最優化目標函數為：

圖1 重力ICCP 算法原理圖Fig.1 ICCP algorithm implementation

其中，X={xi,i=1,2…N}為INS 指示軌跡點集，Y={yi,i=1,2…N}為最近等值線點集為向量l2范數的平方，R為旋轉矩陣，t為平移矢量。

在求解剛性變換的過程中，考慮到旋轉和平移變換的不可交換性，需明確對X先做旋轉變換R，再做平移變換t，即TX=RX+t。則剛性變換求解數學模型為：

可利用四元數法對旋轉矩陣R和平移矢量t進行求解。首先分別以為原點建立新的坐標系，對INS 指示軌跡點xi和最近等值線點yi進行轉換：

在求解旋轉矩陣R時，可先令平移矢量t′=02×1，將式(6)平方展開可得：

利用四元數法即可求解旋轉矩陣R和平移矢量t，并對INS 指示航跡點集應用求解的剛性變換，進行迭代求解。當迭代次數達到預設上限或旋轉矩陣和平移矢量增量的絕對值都小于預設閾值時，停止迭代。基于上述原理可以看出，ICCP 算法遵循“初始對準—尋找對應關系（最近點）—求解使得目標函數最小的變換—應用變換”的循環過程[13]，在等值線上尋找全局最優解，該全局最優解就是最終的匹配結果。

1.2 ICCP 算法的局限性

由ICCP 算法原理可知，該算法是基于兩個前提假設：（1）載體真實位置距離INS 指示位置不遠；（2）重力傳感器沒有測量誤差。該前提假設只是理想狀態，實際中，前者可以通過外部校正信息進行修正，但后者在實際測量中不可實現，重力基準圖的構建以及航行過程中的重力傳感器的實際測量不可避免地存在誤差，所以必須考慮測量誤差對算法的影響。圖2 為在不同噪聲情況下的匹配軌跡，分別是：方案1：無測量噪聲；方案2：加入方差為3 mGal 的高斯白噪聲；方案3：加入方差為5 mGal 的高斯白噪聲。圖3 為三種方案對應的緯向、經向匹配誤差。

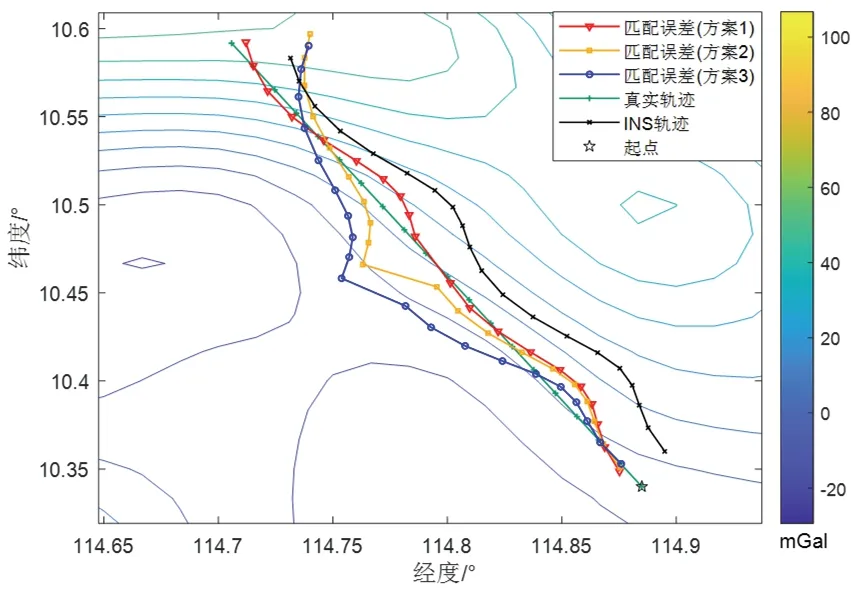
圖2 不同測量噪聲情況下的匹配軌跡Fig.2 Simulation of matching trajectories

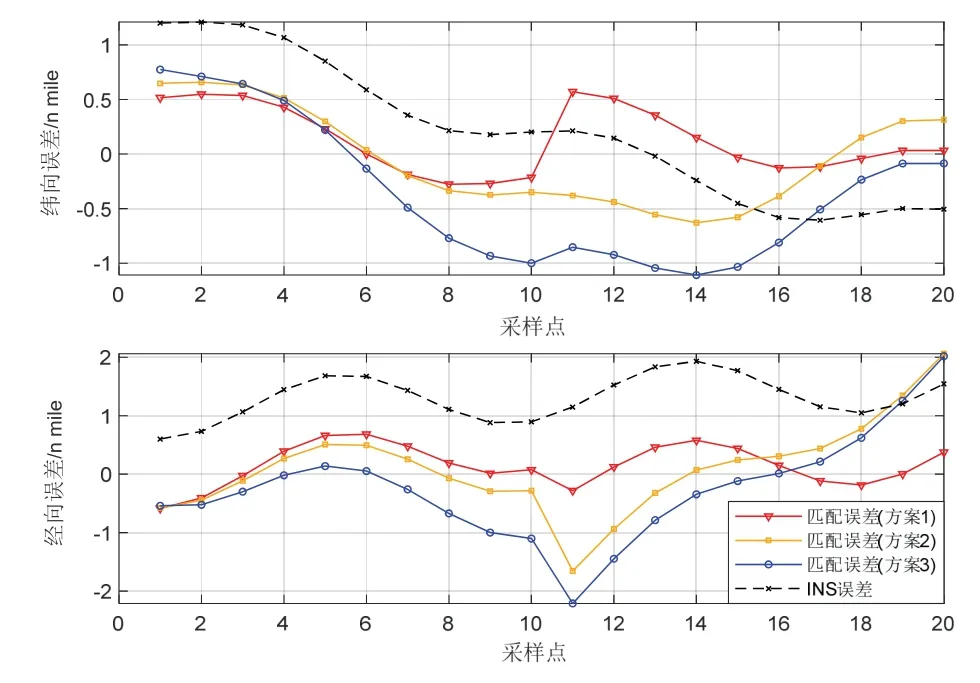
圖3 不同測量噪聲情況下的匹配誤差Fig.3 Simulation of matching error

由圖2 和圖3 可以看出，ICCP 算法在無測量誤差條件下對航行誤差進行校正，可以得出比較高的匹配精度，且較為穩定，但其抗噪聲能力較差；當噪聲較大時，容易發生失配或誤配的情況。故通常先使用其他匹配算法作為粗匹配，再使用ICCP 算法進行精匹配。

1.3 ICCP 誤差分析

針對重力基準圖的構建和實時重力異常的測量產生的誤差對ICCP 算法的匹配精度會產生影響的問題[14]，對ICCP 算法的匹配殘差zi的概率分布進行仿真分析。如圖4 所示，重力傳感器無測量誤差時，匹配殘差zi概率分布如圖4(a)所示；給重力異常測量值增加方差為5 mGal 的高斯白噪聲，匹配殘差zi概率分布如圖4(b)所示。

圖4 匹配殘差 zi概率分布圖Fig.4 Matching residual ziprobability distribution

由圖4(a)可以看出，在無重力測量誤差條件下，ICCP 算法匹配殘差數據直方圖與高斯概率密度擬合較好，此時匹配殘差zi服從高斯分布；由圖4(b)可以看出，在重力異常測量誤差方差為5 mGal 時，ICCP 算法匹配殘差數據直方圖不符合高斯概率密度分布鐘型、對稱、均勻變動的特點，不能較好地擬合，此時匹配殘差zi不服從高斯分布。

此外，由于慣導系統本身存在器件誤差，慣導誤差會隨著航行時間的增加而累積，如果不對其進行抑制，ICCP 算法可能會因為初始誤差較大，而無法找到恰當的最近等值線點，出現誤匹配或匹配失敗的情況。

2 基于 lp范數的HS-ICCP 算法研究

由于ICCP 算法的實質是一個數學優化問題，其目標是通過最小化INS 指示軌跡點集和最近等值線點集之間的歐氏距離，從而實現高精度匹配。該算法可以看作是一個基于l2范數的最小二乘優化問題。最小二乘法是凸優化的一種特殊形式，但其要求匹配殘差服從高斯分布，但在實際情況下，重力異常測量值存在較大誤差，導致匹配殘差不服從高斯分布。因此，考慮重力異常測量誤差會導致匹配點集間的匹配殘差不服從高斯分布的問題，本文應用非凸優化模型來解決這個問題，提出了HS-ICCP 算法，以便更好地處理匹配殘差非高斯分布的情況，提高匹配的準確性。HS-ICCP 算法方案處理流程設計如圖5 所示。

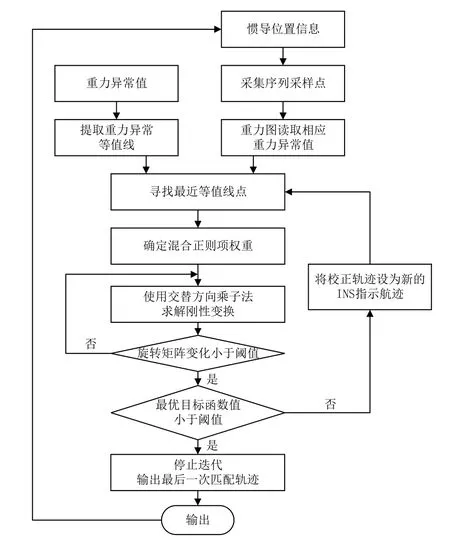
圖5 HS-ICCP 算法流程圖Fig.5 Flow chart of HS-ICCP algorithm

2.1 lp范數

稀疏性問題[15]在變量選擇、圖像處理與計算機視覺等領域中一直受到廣泛關注，壓縮感知理論為解決稀疏性問題提供了理論支撐，許多稀疏性或壓縮感知問題可以轉化為非凸優化問題，如式(9)所示。

lp范數最優化問題是一個非凸、非光滑、非連續的優化問題，可以將lp范數近似逼近于l0范數：

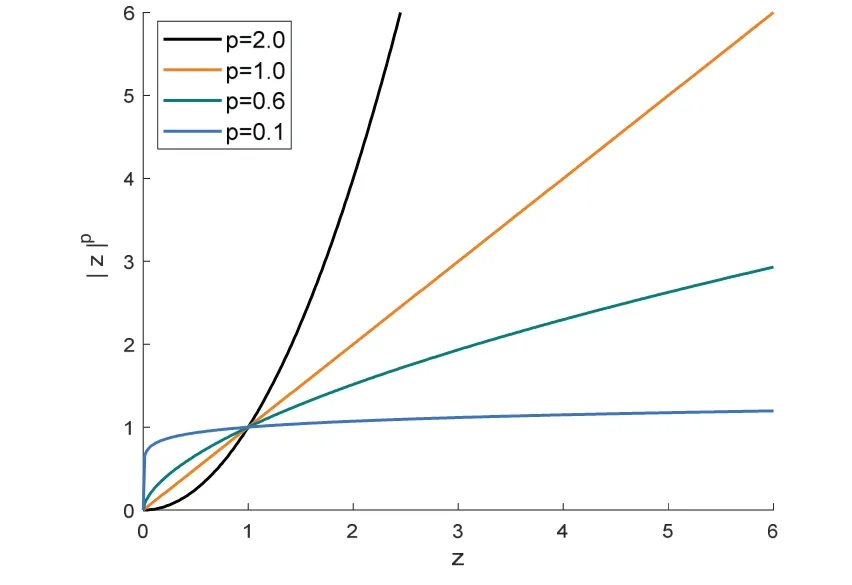
圖6 不同p 取值的范數圖Fig.6 Simulation of different norms

傳統ICCP 算法采用l2范數來最小化INS 指示點集和等值線點集之間的歐氏距離，如圖6 所示，在l2范數的影響下，較大的噪聲會由于距離平方的影響而對總誤差貢獻較大，導致匹配過程可能會被這些異常值所左右；lp范數函數圖像在原點附近急劇變尖，意味著在優化過程中，較小的偏差對總范數的貢獻減少，而較大的偏差導致貢獻加大，有利于剔除掉噪聲點、野值點，實現抗差目的。

2.2 混合稀疏ICCP 函數

理論上重力ICCP 匹配算法是建立在重力傳感器無測量誤差的基礎上，以歐式距離作為最優目標函數進行求解。但實際測量中，重力基準圖的構建和重力傳感器不可避免地存在誤差，且匹配殘差不服從高斯分布，故使用增廣拉格朗日函數建立非凸優化模型，用稀疏誘導lp范數代替l2范數[17]，在保證lp范數的物理意義，同時不影響運算結果的情況下為簡化運算，對lp范數進行放大，將lp范數內部的p次冪運算放大為歐氏距離的2 次冪運算，即令定義稀疏ICCP 如下：

其中，xi為INS 指示軌跡點，yi為最近等值線點，R為旋轉矩陣，t為平移矢量。求解式(12)可將其分解為查找等值線點和求解剛性變換兩個步驟：

對于此公式仍可以使用經典ICCP 算法的最近等值線點搜索方法進行求解。

對于式(14)的求解，則采用增廣拉格朗日算法。引入中間變量Z={zi?R2,i=1…n}，其中，匹配殘差zi=Rxi+t-yi，并將其轉換成如下形式：

引入增廣拉格朗日函數，將式(16)轉化為無約束優化模型：

式(13)和式(14)定義了一個優化問題，目的是將匹配殘差zi分為非異常值和一小部分異常值其中非異常值來自于正確的對應點，異常值來自于錯誤或者噪聲造成的對應點，故可以通過分類目標找到一個稀疏向量z來實現分類目標的目的。

由于式(16)受到單一的p階次正則項的限制，泛化性較差。所以在式(16)的基礎上，使用加權的混合正則項，可以更泛化地表示匹配殘差zi，定義混合稀疏ICCP（HS-ICCP）函數如下：

其中,θi? [0,1]為混合正則項的平衡權重。

通過增廣拉格朗日方法，將式(18)轉化為如下形式：

式(19)中含有四個未知變量，可通過交替方向乘子法（Alternating Direction Method of Multipliers,ADMM）將問題分解為三個步驟進行求解：

Step1：求解匹配殘差z。

Step2：利用Step1 得到的匹配殘差z，求解旋轉矩陣和平移矢量。

Step3：更新懲罰系數μ與拉格朗日乘數λi。

該步驟是對懲罰系數μ進行更新。其中，t指的是第t次迭代，目的是為了增大懲罰系數μ，使Step2 中的(zi+yi-λi/μ)變化盡可能小，防止懲罰系數過小導致最佳位置錯過，故取μ=0.5，a=1.1。

2.3 平衡權重的確定

為了高效地求解式(20)，先驗地認為INS 指示點集經匹配算法計算后，會收斂于正確的匹配位置。對于歐氏距離較大的最近等值線點，增加平衡權重θi會增加其被分類為噪聲點的概率，從而更好地利用p階正則項的稀疏懲罰能力。而對于歐氏距離較小的最近等值線點，降低平衡權重θi會增加其被分類為正確點的可能性，可以更好地利用l2范數正則項的最小二乘逼近能力。

Sigmoid 是二元分類過程中經常使用的函數，使用Sigmoid 函數[18]構建平衡權重θi和每一個INS 采樣點與對應最近等值線點間的歐式距離di的關聯函數：

其中，Median 為INS 采樣點集與其對應最近等值線點集對之間歐氏距離的中位數。

為了弱化離群點，充分進行懲罰，HS-ICCP 的稀疏性應隨著迭代次數的增加而增強，即在匹配過程中，Median 只在外循環搜索最近等值線點結束后計算作為初始值，并在每次外循環迭代過程中逐漸減小為上次迭代的ν倍。隨著Median 的減小，平衡權重θi將逐漸趨近于1。

圖7 為不同Median 對應的Sigmoid 函數圖像，由圖可直觀看出Median 不斷減小為上次迭代的ν倍的變化趨勢，但變化幅度不應過大，若變化幅度過大則會出現過渡較快的情況，就失去了平衡權重的意義，故本文將v 取0.9，可以達到均勻過渡的效果，能更好地對等值線點進行分類。

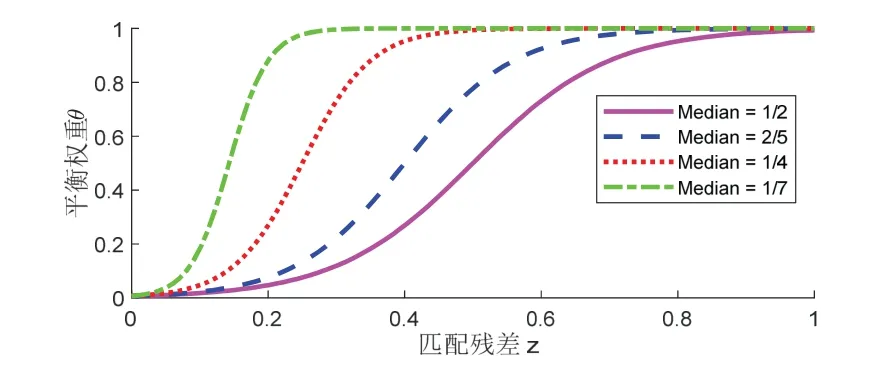
圖7 不同Median 對應的Sigmoid 函數Fig.7 Sigmoid function with different median

2.4 標量化誤差函數

由于式(20)中的匹配殘差zi為向量形式，不易進行求解，故我們使用MM[19（]Majorization-Minimization）算法處理該優化問題。根據式(20)建立其誤差方程：

這里z=(zx,zy)，h=(hx,hy)均為矢量，將z=(zx,zy)用h=(hx,hy)線性表示為z=ah。可以將求解矢量函數(20)中z的最優解簡化為求解標量函數(26)中a的最優解：

對標量函數求標量參數a的偏導數可得：

對g(ah) 求二階偏導數，可得：

由于g′(ah) ＞ 0，可知g(ah) 為凸函數，存在全局最小極值。只有當大于g(ah) 的極小值時，ah才有解，否則令a=0。

在此基礎上，HS-ICCP 算法可以通過ADMM 雙循環的優化架構，使用外循環尋找最近等值線點，計算其對應的歐氏距離，并動態調整平衡權重，利用內循環不斷求解其剛性變換矩陣T=(R,t)。最終弱化離群點以及噪聲點的影響，并實現匹配。

3 重力聯合抗差匹配算法流程

通過上述算法分析可知，HS-ICCP 算法使用lp范數作為距離度量函數，通過ADMM雙循環優化架構，對離群點、噪聲點進行懲罰，起到了削弱重力傳感器測量誤差影響的作用，但匹配精度會有所下降。而在理想條件下，經典ICCP 算法具有穩定性好、精度高的特點。基于以上原因，本文提出一種重力聯合抗差匹配算法，考慮重力傳感器測量誤差，先通過HS-ICCP算法粗略匹配，提供有效的匹配區域，將匹配后的大致位置作為新的INS 指示航跡輸入經典ICCP 算法中進行精確匹配。

重力聯合抗差匹配的具體流程如圖8 所示。

圖8 重力聯合抗差匹配流程圖Fig.8 Flow chart of gravity combined robust matching

綜上，重力聯合抗差匹配導航算法的具體步驟設計如下：

（1）將INS 指示軌跡的累計誤差作為閾值，選取重力匹配區域，建立重力異常基準圖，以保證該區域能涵蓋匹配航跡；

（2）基于INS 指示航跡，使用HS-ICCP 算法進行粗匹配，對含有噪聲的重力異常數據進行處理；

（3）將粗匹配的結果作為精匹配的初始INS 指示航跡，使用經典ICCP 算法進行精匹配；

（4）將精匹配的結果作為新的初始INS 指示航跡重復進行精匹配，直至達到收斂條件；

（5）將收斂后的匹配結果輸出，作為校正航跡。

4 實驗驗證與分析

4.1 仿真實驗設計

為了驗證匹配算法的有效性，選取黃海內一片區域進行測試，通過仿真得到載體的航行路線。表1 給出了仿真線路的起始點坐標、初始誤差、慣導系統陀螺儀、加速度計誤差、航向角、航行速度等參數，重力異常基準圖選用ICGEM 網站提供的SCG-UGM-2模型[21]，分辨率為1′ × 1′，階數為2190 階，精度為1～5mGal。

表1 仿真航跡及其參數Tab.1 Simulated path and their parameters

4.2 仿真實驗

采用表1 中的參數，參考文獻[14][16-18]并經測試驗證p取值0.4～0.6 效果較好，權衡算法性能和魯棒性，本文取p=0.5，ν=0.9，INS 指示航跡采樣間隔為10 min，匹配序列長度為10，使用ICCP 算法和聯合匹配算法對試驗線路進行測試。其中線路所在區域重力基準圖的緯度范圍為31.5°N～32.5°N，經度范圍為121.3°E～122.3°E，重力異常變化范圍為-23.37 mGal～14.71 mGal，基準圖分辨率為1′ × 1′。

實驗一：在INS 運行正常，重力傳感器實時測量無誤差的情況下，兩種算法得到的匹配軌跡如圖9 所示。其匹配結果以及慣導航跡的緯向、經向誤差如圖10所示。

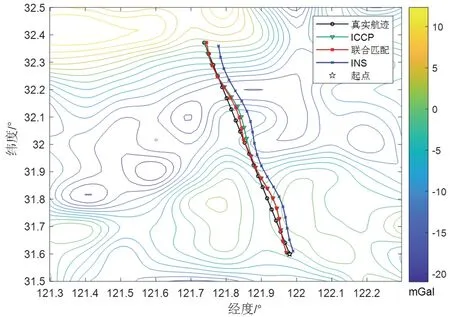
圖9 實驗一匹配軌跡Fig.9 Matching trajectory of experiment one

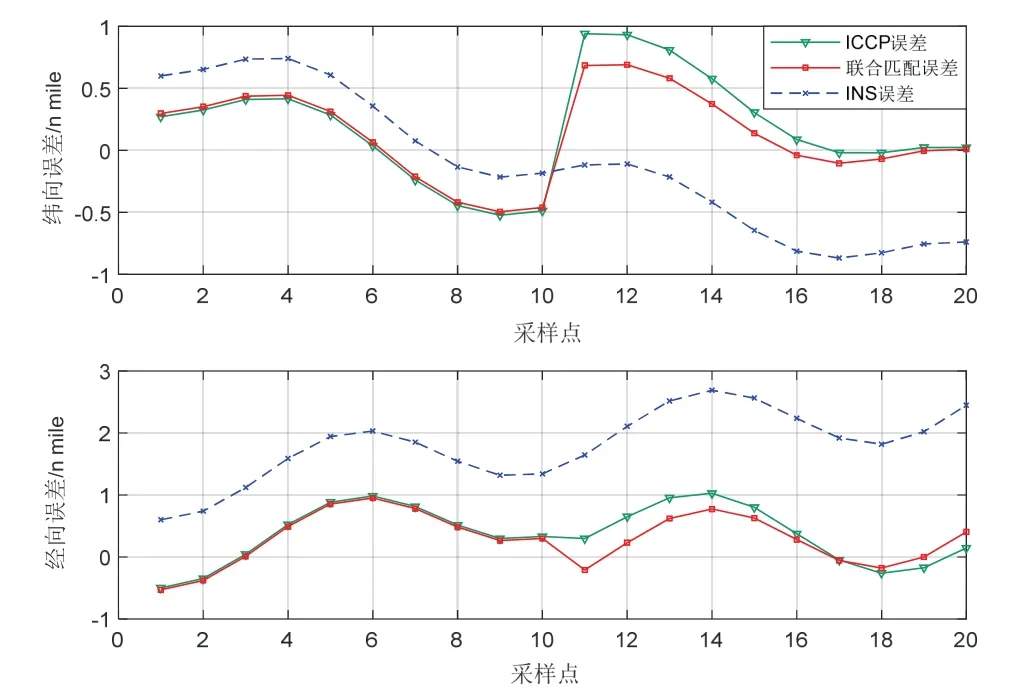
圖10 實驗一匹配誤差Fig.10 Matching error of experiment one

表2 為重力傳感器無測量誤差時，INS 以及兩種算法的誤差參數對比，其中位置誤差表示匹配位置與真實位置之間的直線距離誤差。從表2 中的數據以及圖9 中等值線分布可以看出，在前10 個采樣點進行匹配時，重力異常變化范圍在 -10～0 mGal，且變化較為緩慢，致使兩種算法匹配精度相當；在后10 個采樣點進行匹配時，重力異常變化范圍在 -20～5 mGal，且相鄰點間變化明顯，更有利于重調野值點進行匹配，故聯合匹配算法匹配精度略好于ICCP 算法。從各項數值分析來看，聯合抗差匹配算法在無重力測量誤差的情況下可以正常使用，且導航精度要高于ICCP 算法。

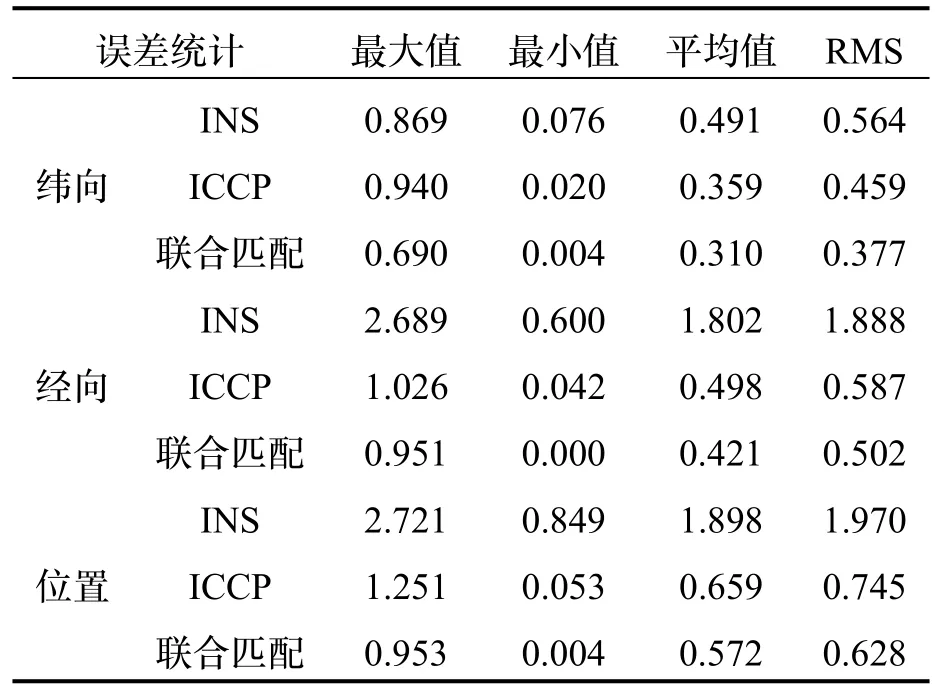
表2 實驗一匹配誤差參數對比（單位：n mile）Tab.2 Comparison of matching error parameters in experiment one (Unit: n mile)

為了更好地與重力傳感器無測量誤差時的仿真結果進行對比，給重力傳感器持續加入不同均值的噪聲進行仿真實驗。

實驗二：噪聲方差為3 mGal 時，兩種算法得到的匹配軌跡如圖11 所示。其匹配結果以及慣導航跡的緯向、經向誤差如圖12 所示。

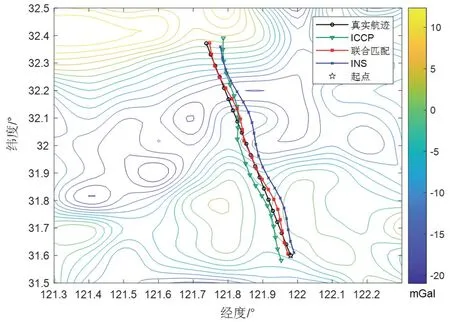
圖11 實驗二匹配軌跡Fig.11 Matching trajectory of experiment two

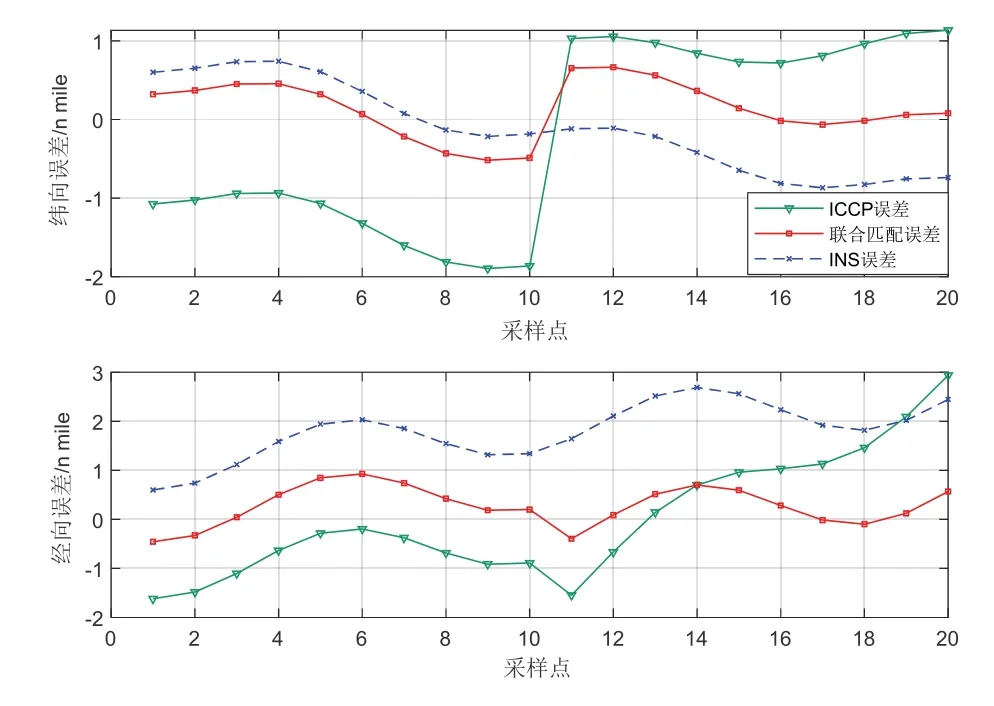
圖12 實驗二匹配誤差Fig.12 Matching error of experiment two

表3 為重力傳感器噪聲方差為3 mGal，INS 以及兩種算法的誤差參數對比。結合圖表信息分析，聯合匹配算法相較ICCP 算法更為穩定，緯向誤差、經向誤差和位置誤差最大值均控制在1 n mile 以內，誤差的平均值最大為0.562 n mile。采用聯合匹配算法計算得到的匹配導航結果精度提升較ICCP 算法提升60%以上。

表3 實驗二匹配誤差參數對比（單位：n mile）Tab.3 Comparison of matching error parameters in experiment two (Unit: n mile)

實驗三：噪聲方差為5 mGal 時，兩種算法得到的匹配軌跡如圖13 所示。其匹配結果以及慣導航跡的緯向、經向誤差如圖14 所示。

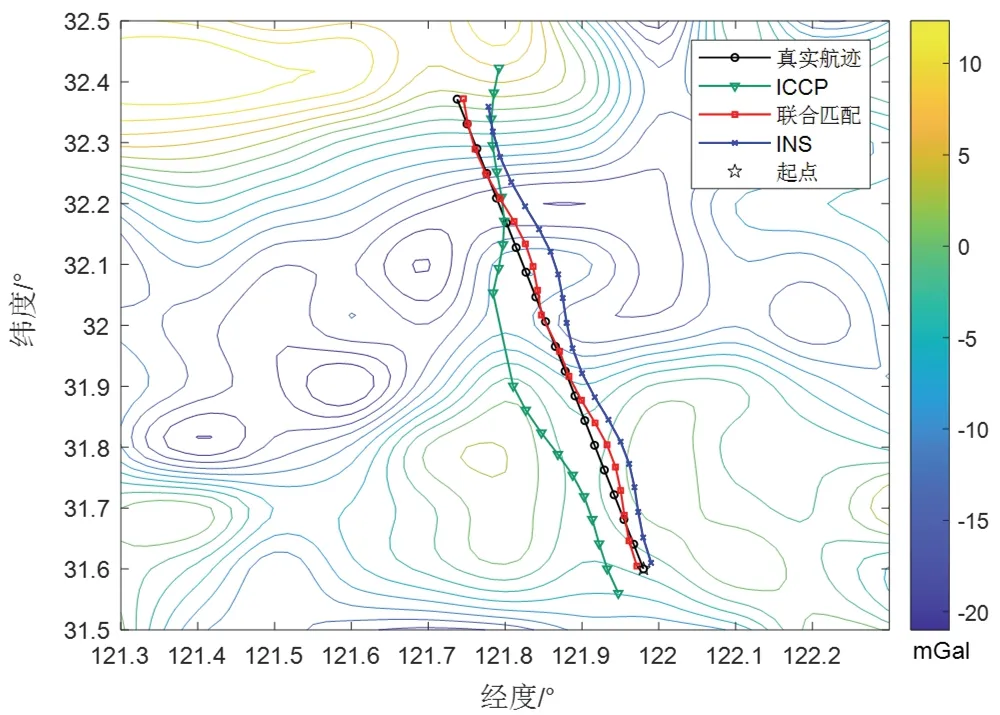
圖13 實驗三匹配軌跡Fig.13 Matching trajectory of experiment three

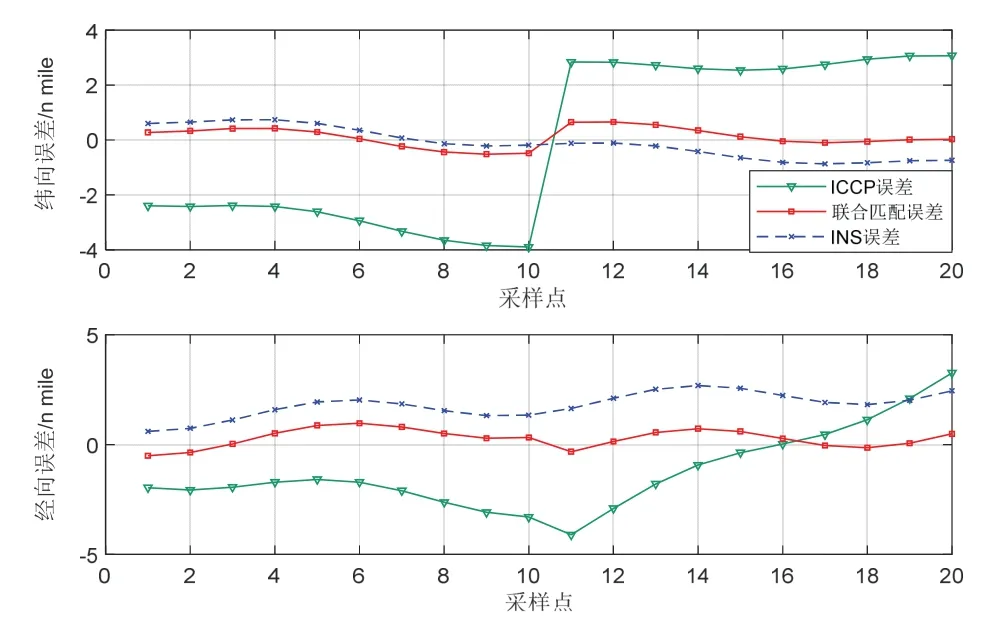
圖14 實驗三匹配誤差Fig.14 Matching error of experiment three

表4 為重力傳感器噪聲方差為5 mGal 時，INS 以及兩種算法的誤差參數對比。此時重力傳感器的測量誤差較大，從軌跡圖上可以看出，ICCP 算法已經產生較大幅度的偏離，而聯合匹配算法仍可以較好地定位到真實航跡，匹配誤差平均值和RMS 都控制在1 n mile 以內，且誤差的平均值最大為0.571 n mile。采用聯合匹配算法計算得到的匹配導航結果精度較ICCP 算法提升75%以上。

對比不同測量誤差下，各算法的位置RMS 值，如圖15 所示：

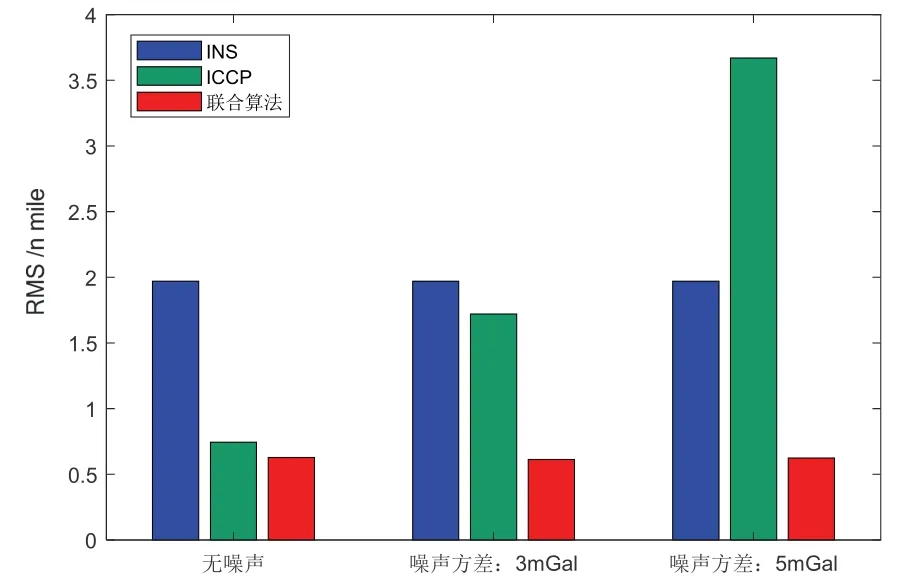
圖15 各算法位置RMS 直方圖Fig.15 Radial RMS histogram of each algorithm

從圖15 可以看出，隨著測量噪聲的不斷增加，ICCP 算法的位置RMS 值也隨之增加，而聯合匹配算法的位置RMS 值維持在穩定范圍內，且波動不大。由此可驗證本文提出的重力聯合抗差匹配算法能夠有效抑制重力傳感器測量誤差對匹配結果的影響，降低匹配誤差。

5 結論

針對重力測量誤差導致匹配殘差不服從高斯分布，使得經典ICCP 算法匹配精度下降甚至失效的問題，提出了一種基于混合稀疏ICCP 的重力聯合抗差匹配導航方法。利用lp范數代替l2范數計算匹配殘差重調野值點，組成以基于lp范數的混合稀疏ICCP 算法為粗匹配、ICCP 算法為精匹配的重力聯合抗差匹配算法。實驗結果表明，在無重力異常測量誤差的情況下，重力聯合抗差匹配算法的匹配精度略優于傳統ICCP；在存在重力異常測量誤差的情況下，重力聯合抗差匹配算法對匹配精度的改善效果明顯，其誤差最大值穩定在1 n mile 以內，誤差均值小于0.572 n mile，誤差RMS 小于0.628 n mile，導航精度較傳統ICCP 算法提升60%以上，可以達到抗重力異常測量誤差的效果，提高了匹配算法的魯棒性。