多車環(huán)境下智能貨車的緊急轉(zhuǎn)向決策及軌跡規(guī)劃

田國富, 張森

(沈陽工業(yè)大學(xué)機(jī)械工程學(xué)院, 沈陽 110870)

中國人口老齡化升高,但運(yùn)輸行業(yè)勞動力需求卻逐漸增加,因此發(fā)展無人駕駛貨車技術(shù)有重要意義。貨車在高速行駛時,當(dāng)前方發(fā)生追尾,急剎停車、甩尾等緊急情況,進(jìn)行緊急剎車,可能導(dǎo)致貨物脫落、剎不住車、側(cè)翻等危險情況,因此針對汽車在突發(fā)情況下進(jìn)行緊急轉(zhuǎn)向避障的決策規(guī)劃成為研究的熱點。

針對換道決策,目前主要分為輕決策和重決策。輕決策是將避障空間進(jìn)行離散化,設(shè)計代價函數(shù),采用動態(tài)規(guī)劃在離散的空間進(jìn)行求解,從而得到凸空間進(jìn)行避障。這種方式可以處理復(fù)雜場景,但這種方式計算量很大,對感知定位要求很高。重決策主要綜合自車與障礙物的距離、相對速度、周圍環(huán)境等信息,根據(jù)人給定的規(guī)則判斷給出決策,主要缺點是場景太多無法覆蓋,但這重決策計算量小,決策時間短。百度的Apollo3.0之前的版本使用的決策為輕決策,Apollo3.5之后的版本采用的是重決策。

軌跡規(guī)劃分為全局和局部,全局路徑規(guī)劃有A star算法、Dijikstra算法等一些比較經(jīng)典的算法和蟻群算法等一些智能算法,局部軌跡規(guī)劃的主要方法主要有多項式曲線插值法、改進(jìn)人工勢場法、貝塞爾曲線法、B樣條曲線法等,文獻(xiàn)[1]采用雙五次多項式方法進(jìn)行軌跡規(guī)劃,相比較五次多項式具有較高的實時性,但該規(guī)劃方法未考慮目標(biāo)車道上行駛的車輛對自車的影響。文獻(xiàn)[2]用快速搜索隨機(jī)樹算法對五次多項式進(jìn)行優(yōu)化,提高了算法收斂速度,保證了軌跡的平滑。文獻(xiàn)[3]用傳統(tǒng)人工勢場法進(jìn)行軌跡規(guī)劃,在將引斥函數(shù)進(jìn)行改進(jìn),從而達(dá)到局部避障的目的。文獻(xiàn)[4]采用基于貝葉斯優(yōu)化的XGBoot換道決策,同時采用五次多項式進(jìn)行規(guī)劃提升了換道效率。文獻(xiàn)[5]基于深度學(xué)習(xí)改進(jìn)決策模型,采用三次多項式并用代價函數(shù)求出最優(yōu)的換道軌跡。文獻(xiàn)[6]采用基于模型預(yù)測控制的動態(tài)軌跡規(guī)劃方法,該方法可以達(dá)到較好的避障效果,但由于其在規(guī)劃中計算量大,不適于緊急轉(zhuǎn)向避障的軌跡規(guī)劃。文獻(xiàn)[7]通過建立人工勢場的引斥力函數(shù),規(guī)劃出一條避障軌跡。

針對多車環(huán)境下,前方發(fā)生突發(fā)事件時的智能貨車緊急轉(zhuǎn)向避障的問題,現(xiàn)通過建立模糊規(guī)則,比較左右車道的安全性來決定貨車的行駛動作,同時提出使用三階貝塞爾曲線規(guī)劃出換道軌跡,并對換道距離和最大的側(cè)向加速度進(jìn)行約束,使智能貨車能平穩(wěn)安全地進(jìn)行緊急轉(zhuǎn)向避障。

1 緊急避障策略

當(dāng)無人駕駛貨車在高速行駛時,前方發(fā)生突發(fā)工況,這時需要進(jìn)行緊急避障決策,通過對左右車道的換道條件進(jìn)行安全評估,當(dāng)左右車道只有一個滿足換道條件時,向滿足換道條件的一側(cè)進(jìn)行避障,當(dāng)兩側(cè)都滿足換道行為時,通過比較左右車道安全性大小,使貨車向更安全的一側(cè)進(jìn)行避障,如果都不滿足,則進(jìn)行剎車減速,等到符合轉(zhuǎn)向避障安全時,進(jìn)項轉(zhuǎn)向避障。無人駕駛貨車避障策略如圖1所示。

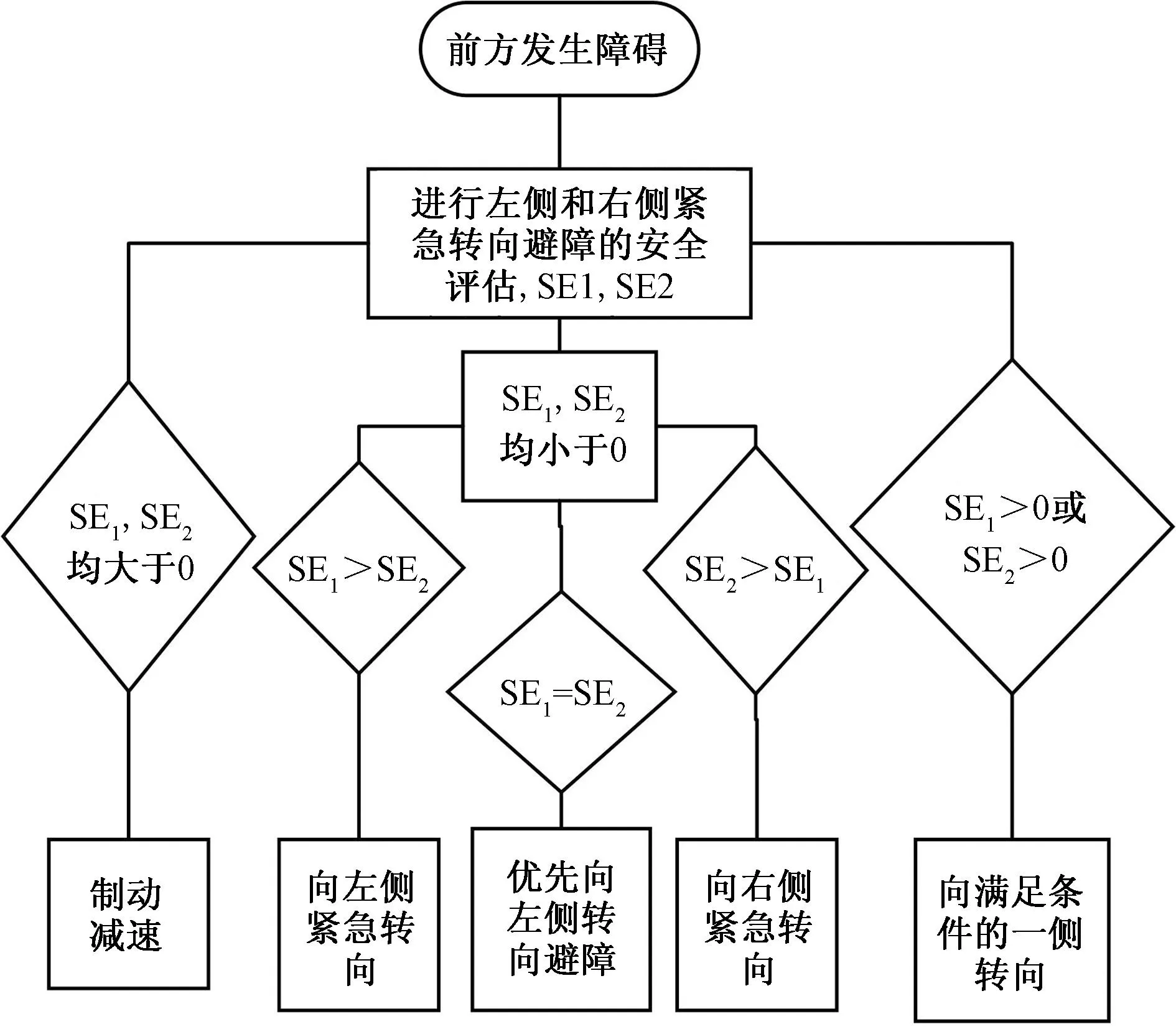
SE1為左車道安全值;SE2為右車道安全值

2 建立換道安全距離

假設(shè)目標(biāo)車道的行駛車輛為人為駕駛,建立自車與目標(biāo)車道后方車輛的轉(zhuǎn)向避障安全距離[8],以后方車輛的緊急剎車距離為換道的最小安全距離,考慮人的反應(yīng)時間,設(shè)反應(yīng)時間為0.5 s,則最小安全距離為

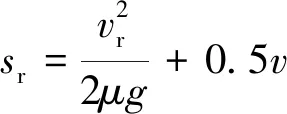
(1)

自車與目標(biāo)車道前方車輛的緊急轉(zhuǎn)向避障最小安全距離為

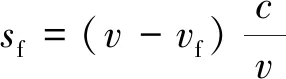
(2)

式中:vr、v、vf分別為轉(zhuǎn)向時目標(biāo)車道的后方車輛速度、自車速度、轉(zhuǎn)向時目標(biāo)車道前車速度;c為前方障礙物與自車的縱向距離。

將自車換道時的安全性依據(jù)兩種最小安全距離建立模糊規(guī)則,將自車與目標(biāo)車道后車的相對距離與最小安全距離的差值D1作為模糊輸入1,語言變量設(shè)為5級,分別為負(fù)(N),零(O),正小(PS),正中(PM),正大(PB),設(shè)目標(biāo)車道汽車的最大行駛速度限制為120 km/h,最小行駛速度限制為60 km/h,令最小安全距離與目標(biāo)車道后車的差值在范圍[-110,-10]為負(fù)(N),[-10,20]為零(O),[10,50]為正小(PS),[40,80]為正中(PM),[60,90]為正大(PB)。隸屬度函數(shù)圖像如圖2所示。

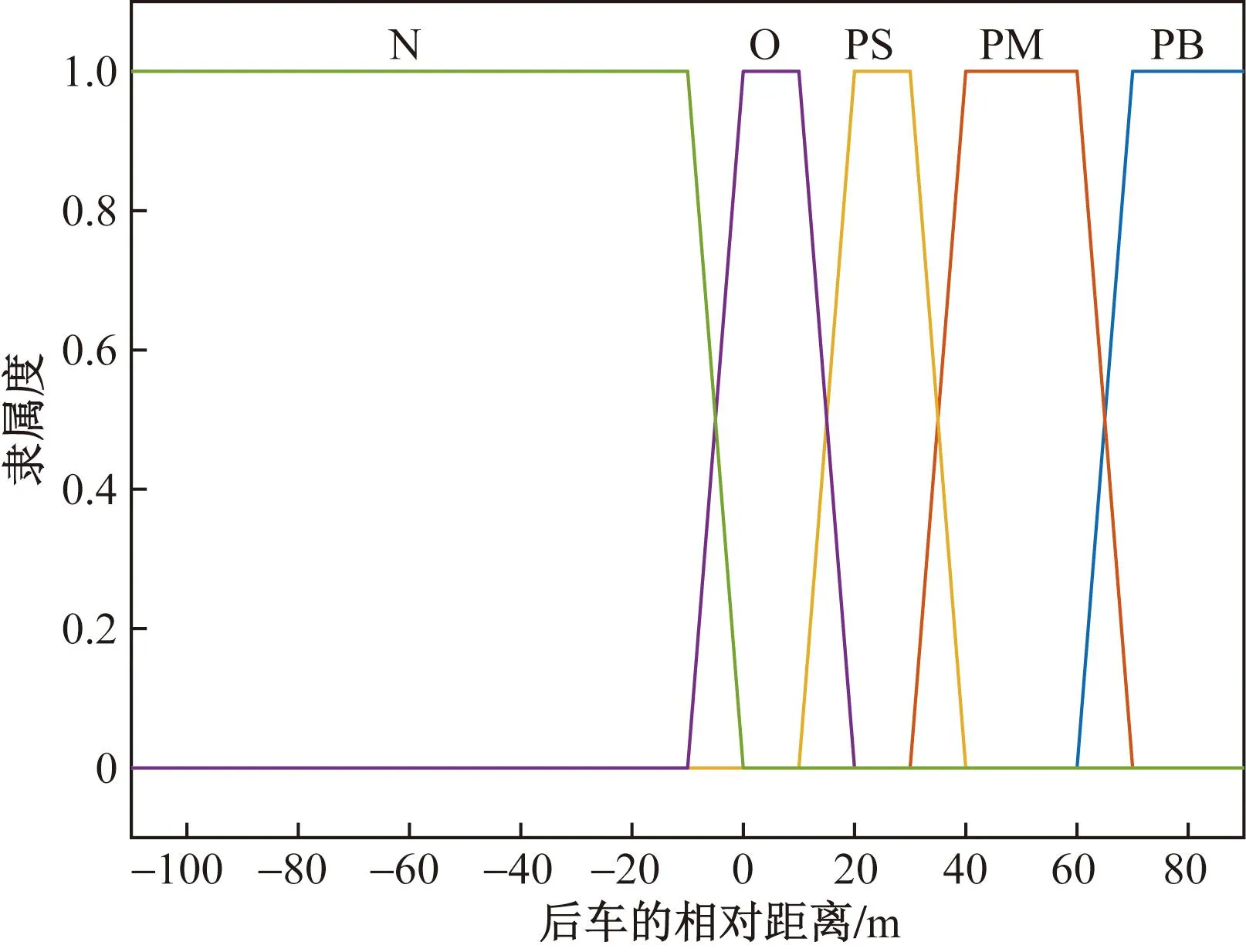
圖2 后車輸入變量的隸屬度函數(shù)

自車與目標(biāo)車道前車的相對距離與最小安全距離的差值D2作為模糊輸入2,令最小安全距離與目標(biāo)車道后車的差值在范圍[-50,-10]為負(fù)(N),[-10,30]為零(O),[20,60]為正小(PS),[50,90]為正中(PM),[80,150]為正大(PB)。隸屬度函數(shù)圖像如圖3所示。

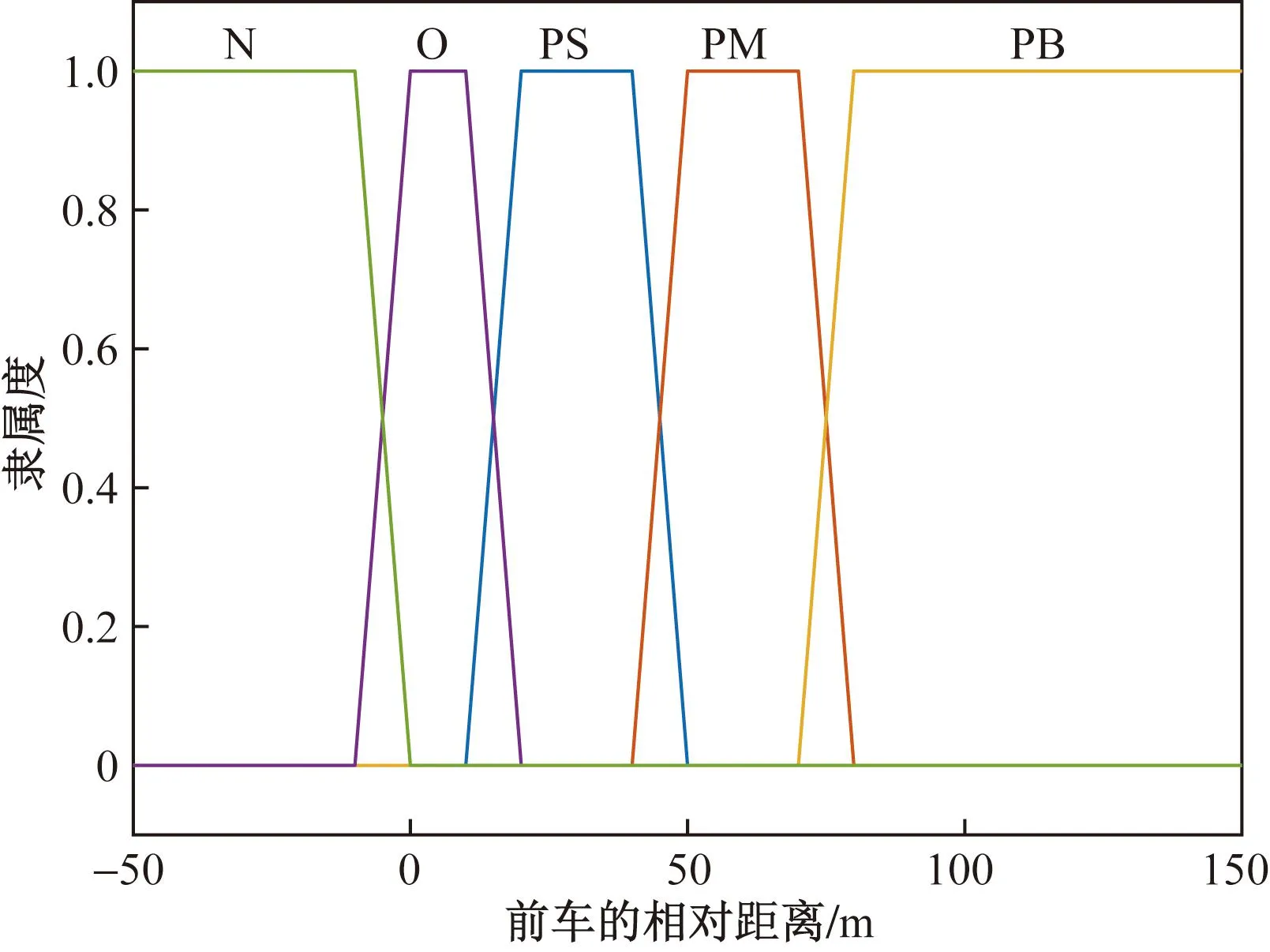
圖3 前車輸入變量的隸屬度函數(shù)

輸出為換道安全值SE,論域為[-1,1],語言變量設(shè)為7級,分別為負(fù)(N)、零(O)、正小(PS)、正中小(PMS)、正中(PM)、正中大(PMB)和正大(PB),隸屬度函數(shù)圖像如圖4所示。通過輸入輸出構(gòu)建模糊規(guī)則如表1所示。

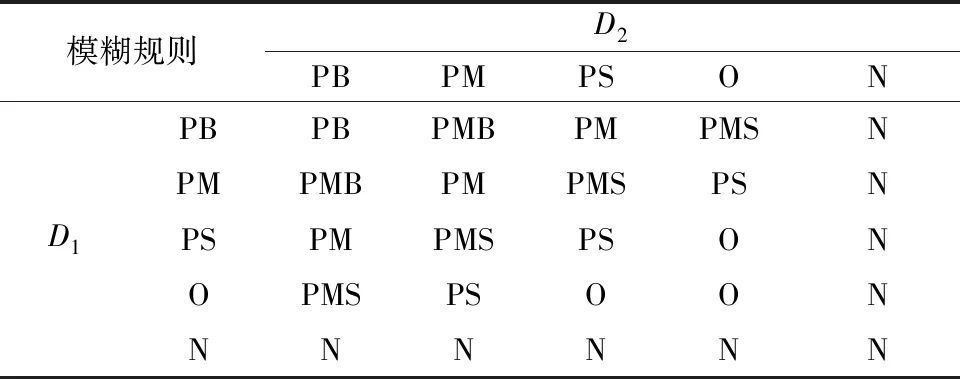
表1 模糊規(guī)則表

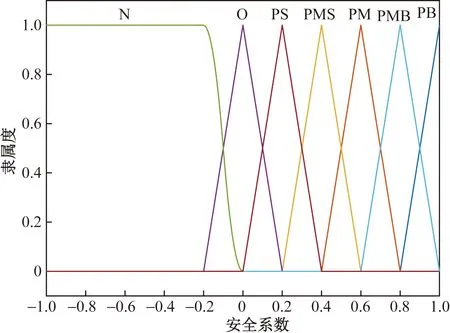
圖4 輸出安全值的隸屬度函數(shù)

在換道決策時將左右目標(biāo)車道上的前車和后車與自車的相對距離分別輸入,然后查找模糊規(guī)則表,通過解模糊求出相應(yīng)的安全值,比較安全值的大小,然后控制車輛向安全值較大的一側(cè)轉(zhuǎn)向避障。

3 局部軌跡規(guī)劃

貝塞爾曲線[9]具有的幾何特性不隨著坐標(biāo)系的變化而變化,曲線的始末控制點分別為曲線的起始點和終止點的特點,使貝塞爾曲線控制簡單,易于跟蹤,經(jīng)常應(yīng)用于無人駕駛汽車的局部避障[10]的規(guī)劃軌跡中,并且還可以通過改變貝塞爾曲線控制點的坐標(biāo)進(jìn)而達(dá)到控制曲線曲率和曲線彎曲方向目的,由于在緊急轉(zhuǎn)向時的軌跡不僅需要具有平滑的曲線和連續(xù)的曲率,而且要求在規(guī)劃時需要更少的計算量來減少計算時間,因為三階貝塞爾曲線與其他高階貝塞爾曲線相比僅需要4個控制點就可以規(guī)劃出一條連續(xù)平滑的軌跡,可以減少規(guī)劃軌跡的計算量,所以選擇三階貝塞爾曲線作為避障規(guī)劃軌跡的曲線。

3.1 貝塞爾曲線公式

設(shè)P0、P1為曲線的兩個控制點,t的取值為0～1,則一階貝塞爾曲線可表示為

p1(t)=(1-t)p0+tp1

(3)

設(shè)P0、P1、P2為曲線的3個控制點,t的取值為0～1,由于P0、P1構(gòu)成一階貝塞爾曲線,P1、P2構(gòu)成一階貝塞爾曲,可得

p1,1(t)=(1-t)p0+tp1

(4)

p1,2(t)=(1-t)p1+tp2

(5)

則在此基礎(chǔ)上可生成二階貝塞爾曲線為

p2(t)=(1-t)p1,1+tp1,2

(6)

通過一二階貝塞爾曲線公式可推出,當(dāng)P0、P1、P2、P3共4個控制點已知時,P0和P1、P1和P2、P2和P3都構(gòu)成一階貝塞爾曲線,即

p1,1(t)=(1-t)p0+tp1

(7)

p1,2(t)=(1-t)p1+tp2

(8)

p1,3(t)=(1-t)p2+tp3

(9)

由3個一階曲線可推出如下的兩個二階曲線

p2,1(t)=(1-t)p1,1+tp1,2

(10)

p2,2(t)=(1-t)p1,2+tp1,3

(11)

由此可推出三階貝塞爾曲線為

p3(t)=(1-t)p2,1+tp2,2

(12)

將式(3)～式(11)代入(12)可得三階貝塞爾曲線的表達(dá)式為

(13)

汽車在直角坐標(biāo)系中的坐標(biāo)為(x,y),需要將曲線公式轉(zhuǎn)換為x,y分別關(guān)于t的函數(shù)。

設(shè)x,y關(guān)于t的參數(shù)方程為

(14)

將式(13)轉(zhuǎn)換為矩陣表達(dá)式為

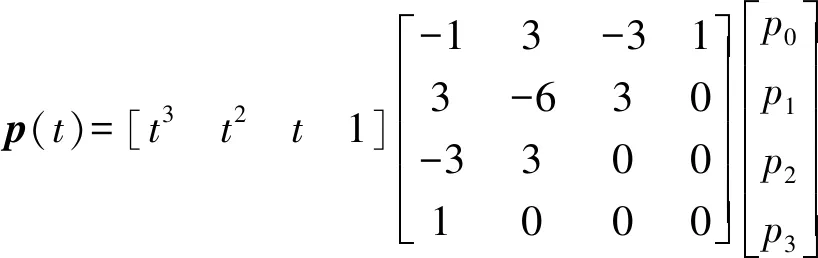
(15)

將式(14)代入式(15)得

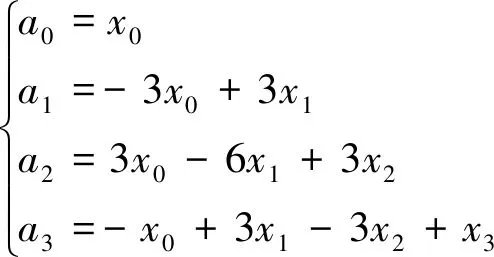
(16)

(17)

回代系數(shù)a、b后整理可得道直角坐標(biāo)系下的三階貝塞爾曲線。

(18)

由曲率的定義可知

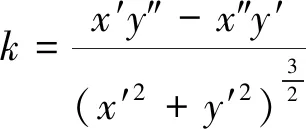
(19)

式(19)中:x′、y′、x″、y″分別為汽車的縱向速度、橫向速度、縱向加速度、橫向加速度。

3.2 確定4個控制點的坐標(biāo)

設(shè)第一個控制點為初始點(0,0),則P0(x0,y0)=(0,0),第二個控制點為P1(x1,y1)假設(shè)車輛初始航向角為0°,則P1(x1,0),第三個控制點為P2(x2,y2),第四個控制點為P3(x3,y3),再換道避障時,為了安全的考慮通常將換道的結(jié)束點的橫坐標(biāo)設(shè)置為道路中心線,由中國道路的標(biāo)準(zhǔn)寬度為3.75 m,可知P3(x3,3.75),P2(x2,3.75),為了更快地計算控制坐標(biāo),規(guī)劃避障軌跡將4個點設(shè)計為中心對稱的形式,如圖5所示,可以得到x2=x1,x3=2x1,P2(x2,3.75)=(x1,3.75),P3(x2,3.75)=(2x1,3.75),由4個控制點坐標(biāo)的表達(dá)式可知,它們都與x1相關(guān)聯(lián),因此只需求出x1的大小就可以將三階貝塞爾曲線的形狀確定。

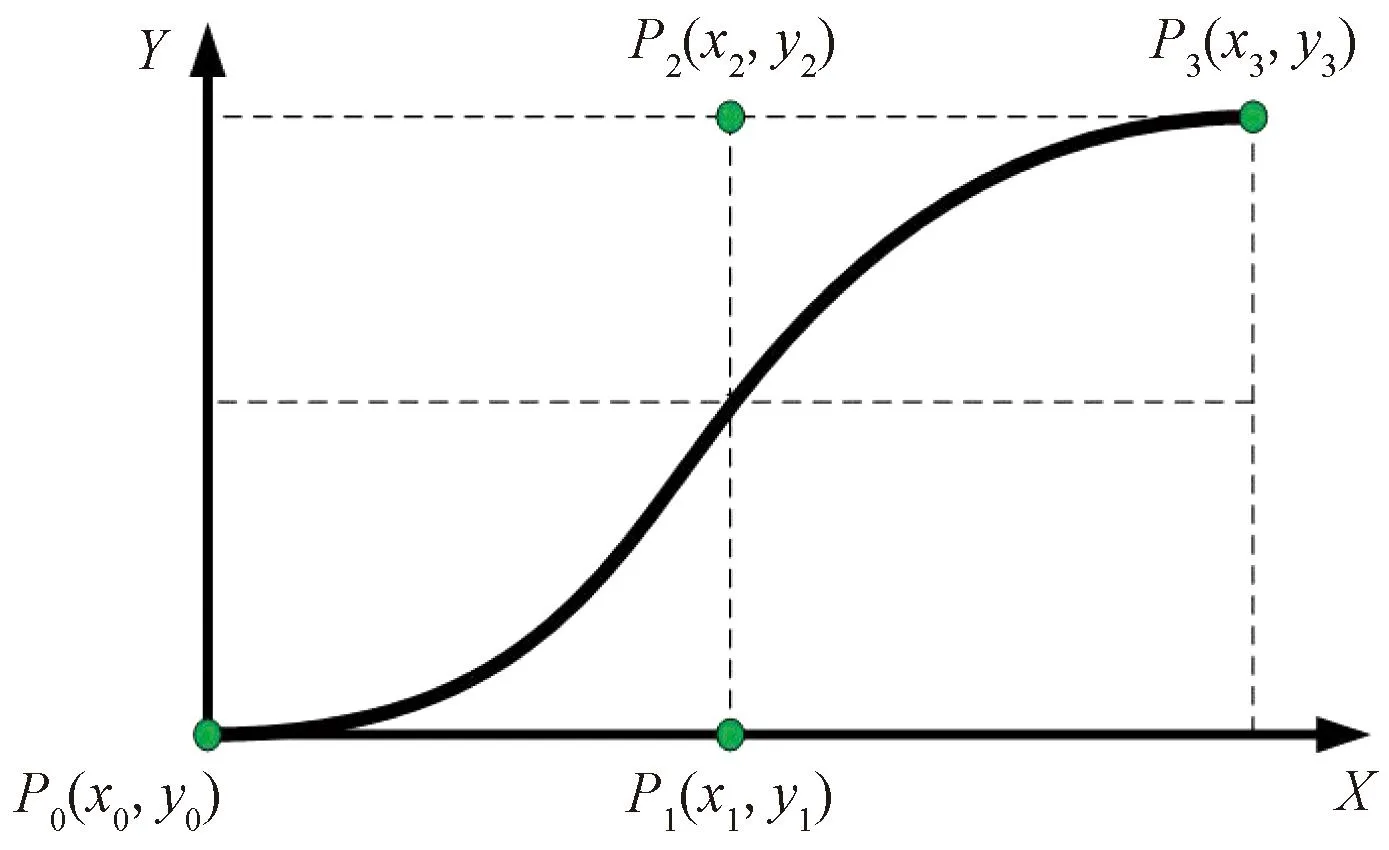
圖5 三階貝塞爾曲線

3.3 規(guī)劃軌跡的邊界約束

針對貨車在緊急轉(zhuǎn)向避障時可能發(fā)生的危險,將對貨車在緊急轉(zhuǎn)向時規(guī)劃軌跡的邊界進(jìn)行約束,如圖6所示。

圖6 規(guī)劃軌跡邊界約束

貨車在進(jìn)行緊急轉(zhuǎn)向時由于自身質(zhì)量大,質(zhì)心高,如果轉(zhuǎn)向時橫向加速度過大,可能會導(dǎo)致貨車發(fā)生側(cè)翻,擺尾等危險情況發(fā)生,為了避免這種危險,要對貨車的橫向加速度進(jìn)行約束。車輛靜態(tài)穩(wěn)定性公式為

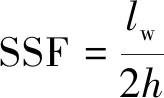
(20)

可以推導(dǎo)出車輛的瞬時平衡方程為

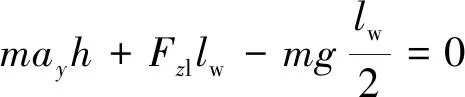
(21)

式中:Fzl為左側(cè)車輪的垂直載荷;ay為轉(zhuǎn)向時的橫向加速度;lw為車輪輪距;h為車輛質(zhì)心高度。

由式(21)得到左側(cè)車輪的垂直載荷為

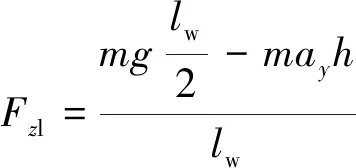
(22)

由式(22)可以得出,當(dāng)橫向加速度為0時,左側(cè)車輪的垂直載荷為mg/2,當(dāng)橫向加速度不斷增大,直到左側(cè)垂直載荷為0時,此時的橫向加速度為

(23)

這時的車輛狀態(tài)為貨車發(fā)生側(cè)翻的初始狀態(tài),aymax為車輛準(zhǔn)靜態(tài)下側(cè)翻的閾值[11]。在實際駕駛中,車輛的瞬態(tài)側(cè)翻閾值明顯小于準(zhǔn)靜態(tài)閾值,一般僅為準(zhǔn)靜態(tài)側(cè)翻閾值的30%～50%[12]。通過仿真實驗的車輛模型數(shù)據(jù)可得到aymax=0.9g,選取動態(tài)側(cè)翻閾值的大小為準(zhǔn)靜態(tài)的30%,則

aymax≤0.27g

(24)

由圖6可知,此時的R1和X1為

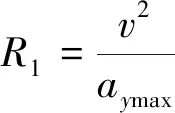
(25)

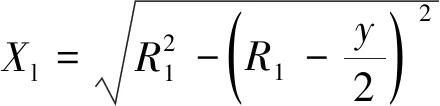
(26)

式中:v為自車行駛速度;Xl為控制點P1(x1,y1)中x1的最小距離。

在避障時需要考慮在換道時是否會與前方障礙物發(fā)生碰撞,對車輛換道時的碰撞邊界進(jìn)行約束。在與前方障礙車輛不發(fā)生碰撞的極限車距進(jìn)行避障,如圖3的碰撞邊界所示,以車輛自身為圓心,r為半徑建立圓形車輛幾何形狀模型進(jìn)行約束分析。

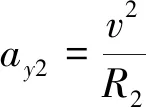
(27)

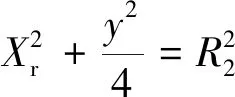
(28)

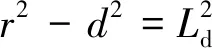
(29)

(30)

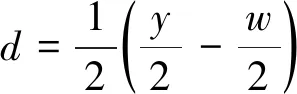
(31)

式中:ay2為碰撞邊界的最大橫向加速度;y為道路寬度;r為車輛半徑;w為車輛寬度;l為車輛長度;d為換道時不發(fā)生碰撞的兩車的最小橫向距離;v為自車縱向速度;Xr為控制點P1(x1,y1)中x1的最大距離。

穩(wěn)定性邊界和碰撞邊界的約束只能規(guī)劃出保證車輛不發(fā)生側(cè)傾和碰撞軌跡,為了規(guī)劃出最合理的軌跡,做下列約束。

(1)在軌跡的初始點應(yīng)使軌跡曲率盡可能趨近于0,這樣可以使車輛更好地對規(guī)劃的軌跡進(jìn)行跟蹤。

(2)由式(27)可知,在換道過程中車輛的轉(zhuǎn)向半徑與車輛的橫向加速度成反比,同時軌跡的曲率與轉(zhuǎn)向半徑成正比,因此在換道過程中對最大橫向加速度的約束可以轉(zhuǎn)為對軌跡的最大曲率的約束。

(3)換道中間位置車輛朝向與車道線之間的夾角θ,應(yīng)滿足0°<θ<45°的條件[13],此約束條件可以變?yōu)楫?dāng)參數(shù)t=0.5時的道路曲率約束。

通過上述約束可設(shè)計代價函數(shù)為

J=min(J1+J2+J3)

(32)

式(32)中:J1=kt=0;J2=kmax;J3=dy/dx(當(dāng)t=0.5時)。各個約束條件[14]如下。

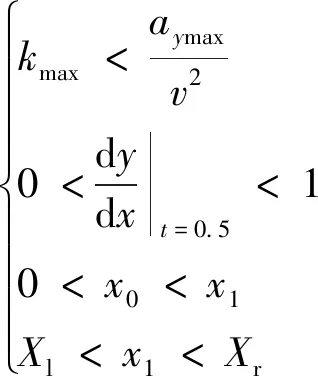
(33)

對上述代價函數(shù)求解[15],采用MATLAB中自帶的fmincon函數(shù)來求解非線性函數(shù)有約束優(yōu)化問題的極小值。

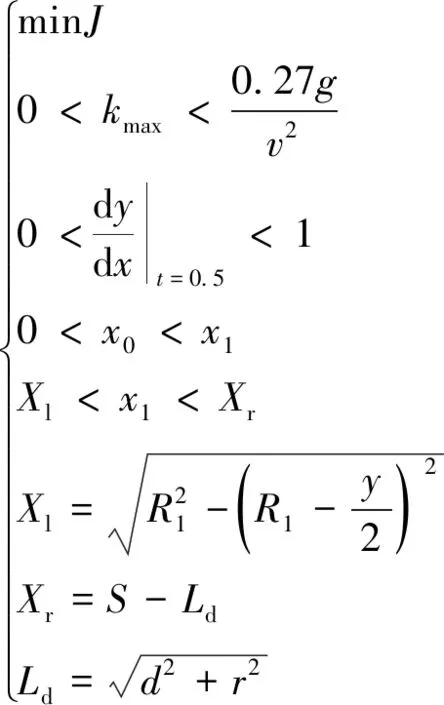
(34)

由式(34)可以求出不同車速下,三階貝塞爾曲線中控制點P1(x1,0)中x1的最優(yōu)解。其中S為距離前車安全的轉(zhuǎn)向車距,一般取值為(2～3)v。根據(jù)P1(x1,0)然后得到控制點P2(x2,y2),P3(x3,y3)的坐標(biāo),從而得到不同車速下對應(yīng)的貝塞爾換道曲線如圖7所示。

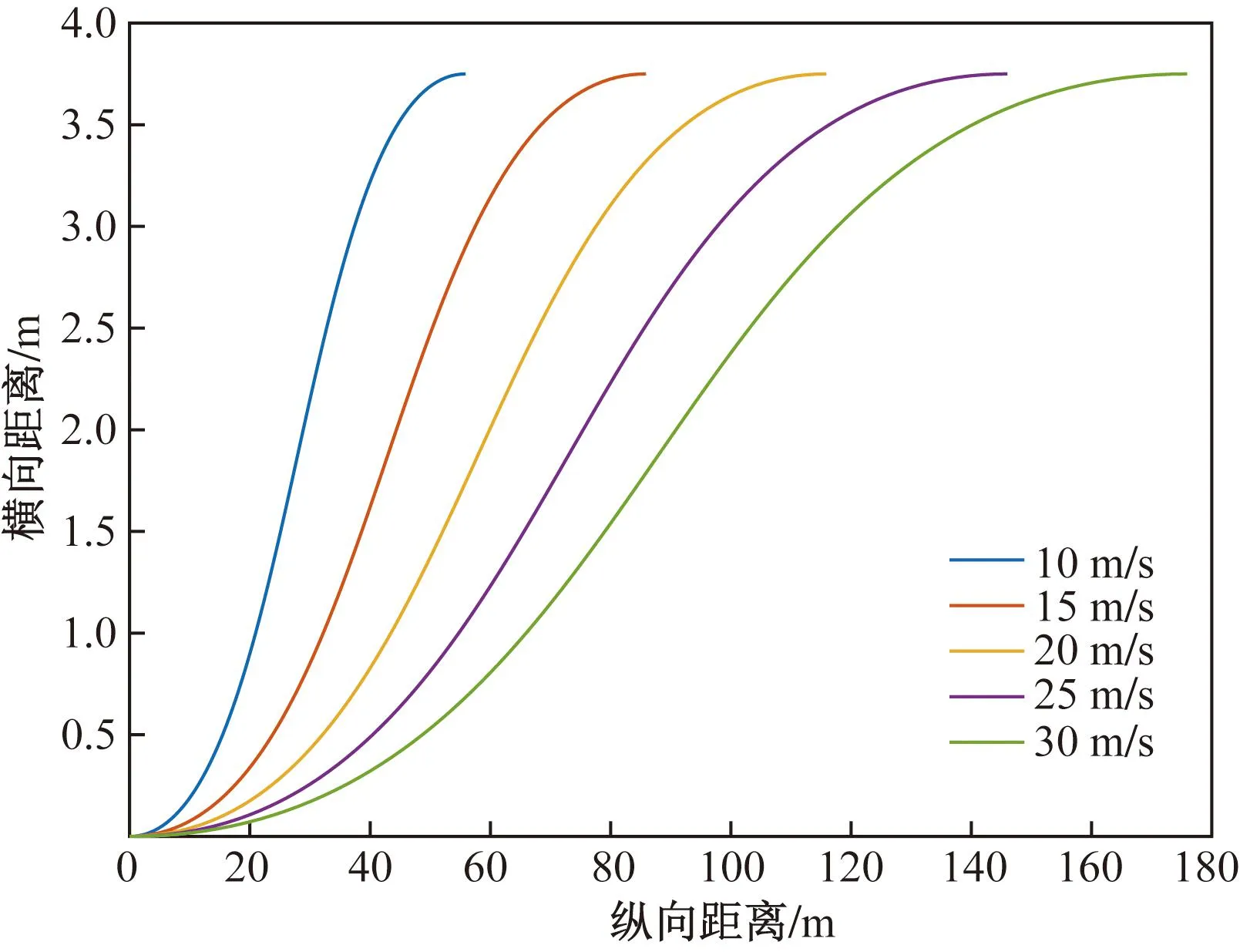
圖7 不同車速下的避障軌跡

低速行駛時貨車轉(zhuǎn)向時發(fā)生側(cè)翻的可能性遠(yuǎn)遠(yuǎn)小于高速行駛時側(cè)翻的可能性,因此對20、25、30 m/s 3種行駛速度所規(guī)劃出的道路曲率進(jìn)行計算,如圖8所示。

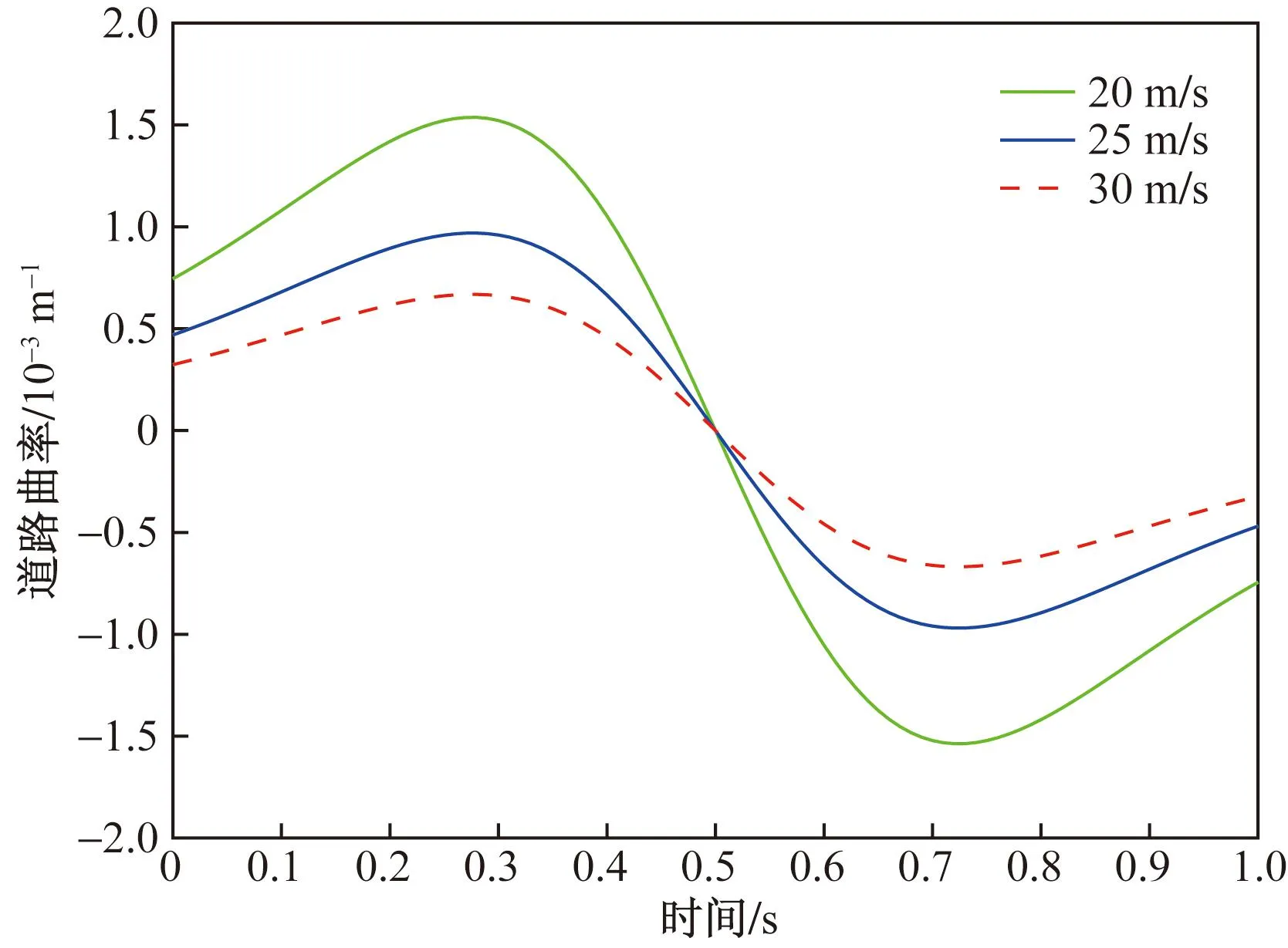
圖8 不同軌跡下的道路曲率

計算得到3種速度對應(yīng)的最大道路曲率分別為0.001 5、0.000 97、0.000 66,均小于對應(yīng)的最大道路曲率值Kmax,則規(guī)劃軌跡滿足轉(zhuǎn)向要求。

4 仿真檢驗

情景一:當(dāng)前方緊急情況,此時自車速度為100 km/h,右側(cè)車道后車速度為90 km/h,與自車距離為20 m,右側(cè)車道前車速度為90 km/h,與自車距離為10 m,左側(cè)車道后車速度為100 km/h,與自車距離為80 m,左側(cè)車道前車速度為100 km/h,與自車距離為70 m。此時右側(cè)不滿足避障條件,左側(cè)滿足避障條件。使用carsim仿真軟件中自帶的utility truck貨車模型進(jìn)行仿真,結(jié)果如圖9～圖11所示。

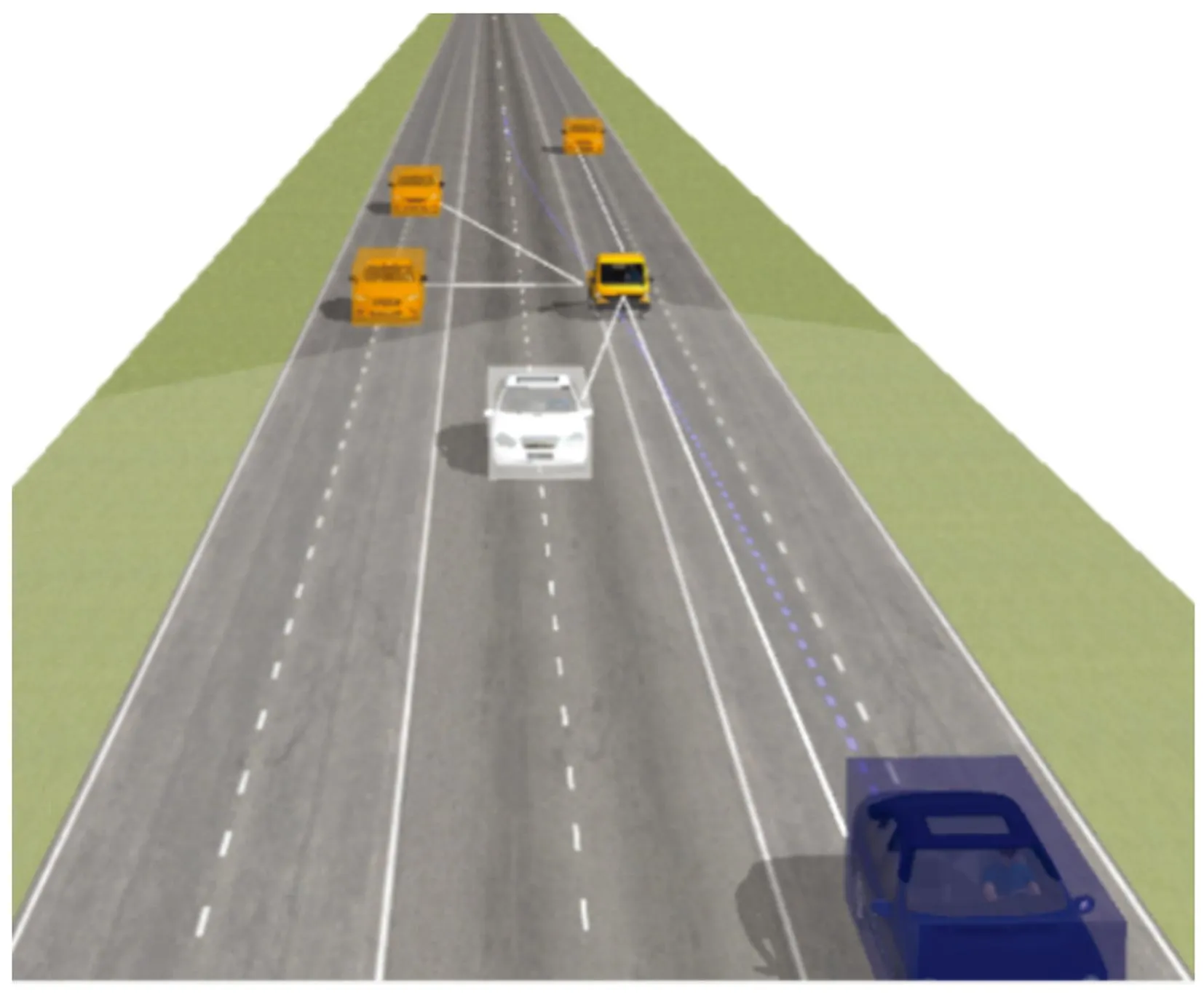
圖9 左側(cè)避障仿真

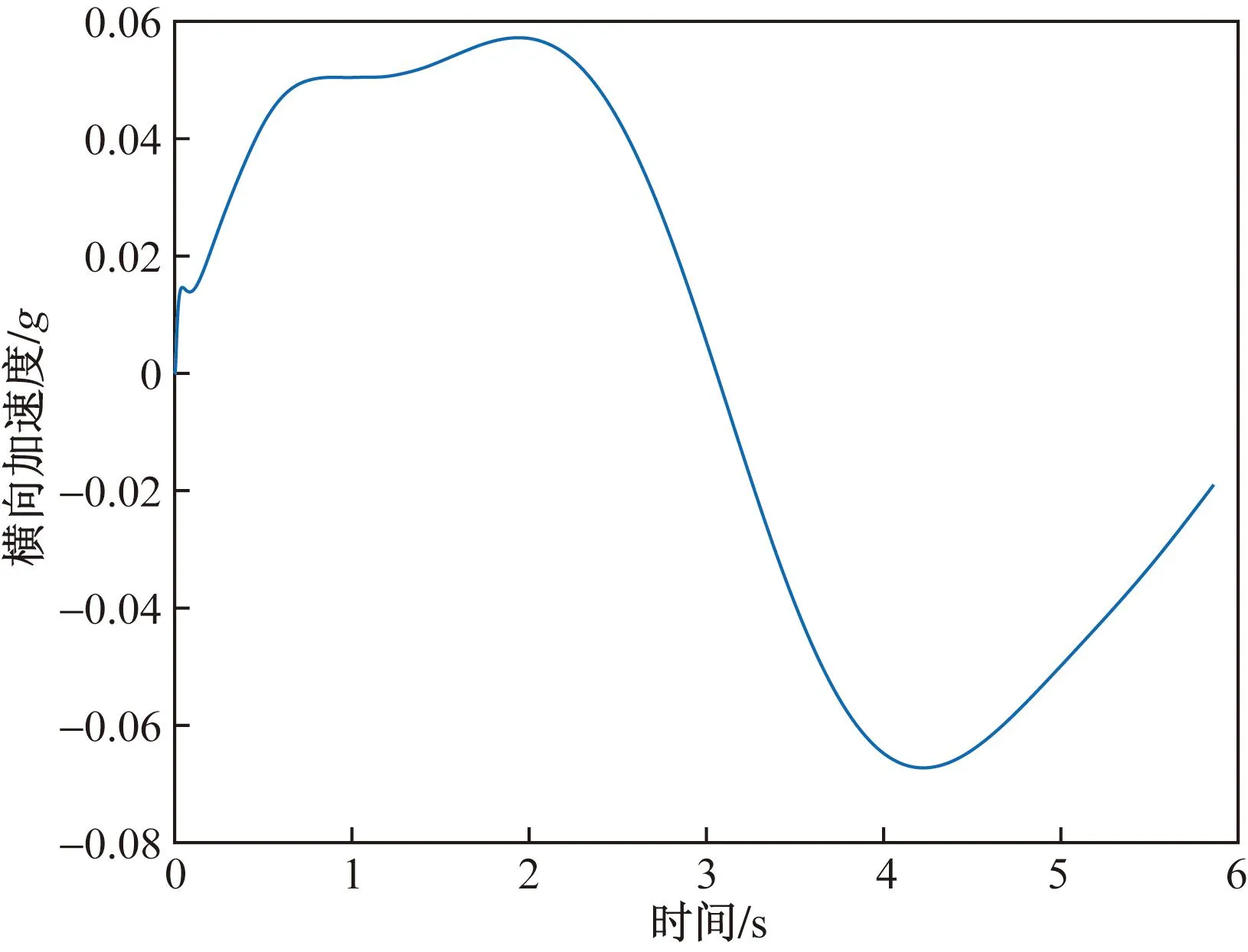
圖10 左側(cè)避障過程中的橫向加速度變化

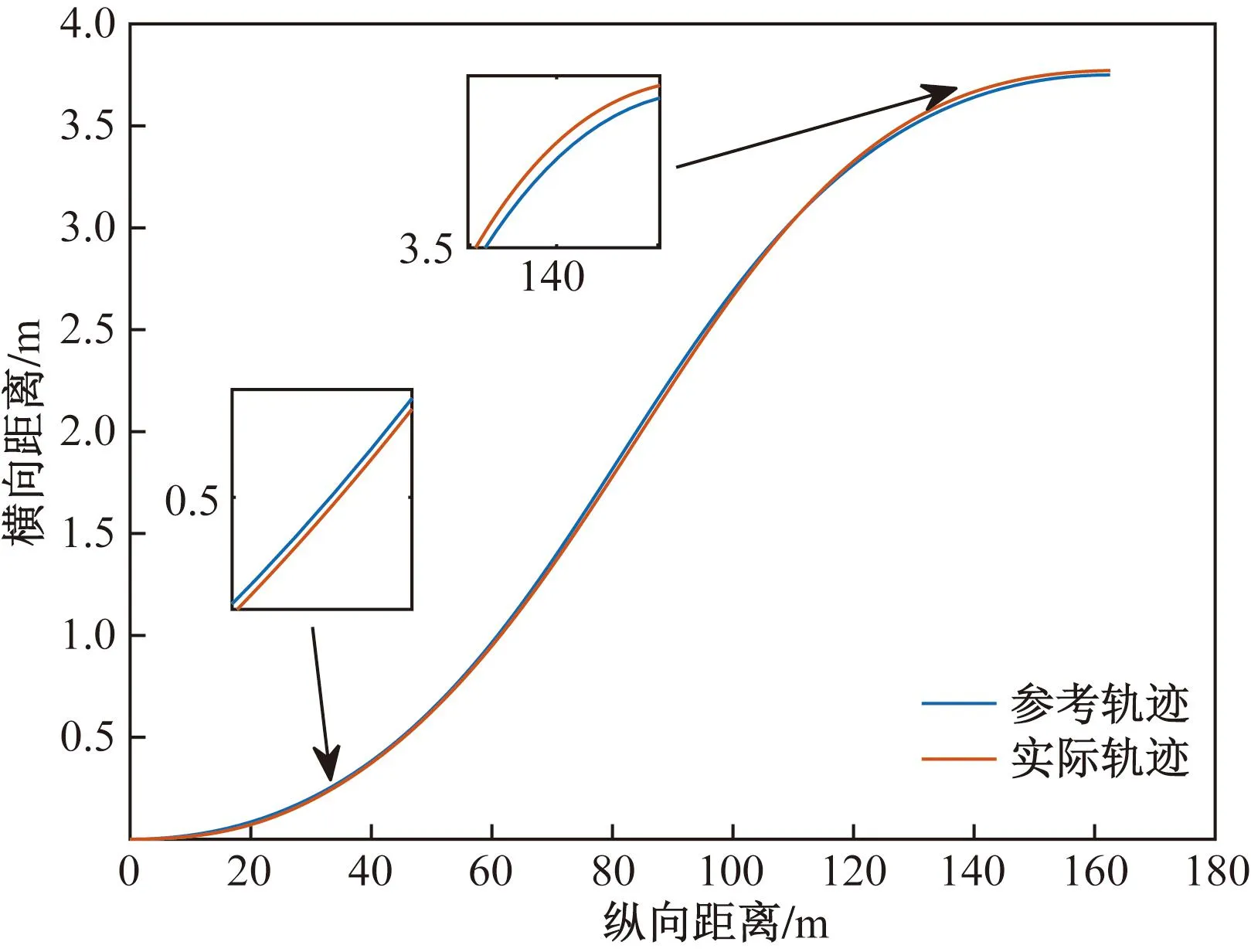
圖11 左側(cè)避障軌跡的跟蹤效果

情景二:前方發(fā)生緊急情況時,此時自車速度為90 km/h,右側(cè)車道后車速度為90 km/h,與自車距離為60 m,右側(cè)車道前車速度為90 km/h,與自車距離為50 m,左側(cè)車道后車速度為100 km/h,與自車距離為20 m,左側(cè)車道前車速度為100 km/h,與自車距離為10 m。此時左側(cè)不滿足避障條件,右側(cè)滿足避障條件,結(jié)果如圖12～圖14所示。

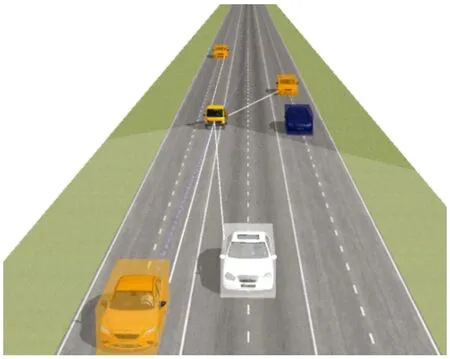
圖12 右側(cè)避障仿真

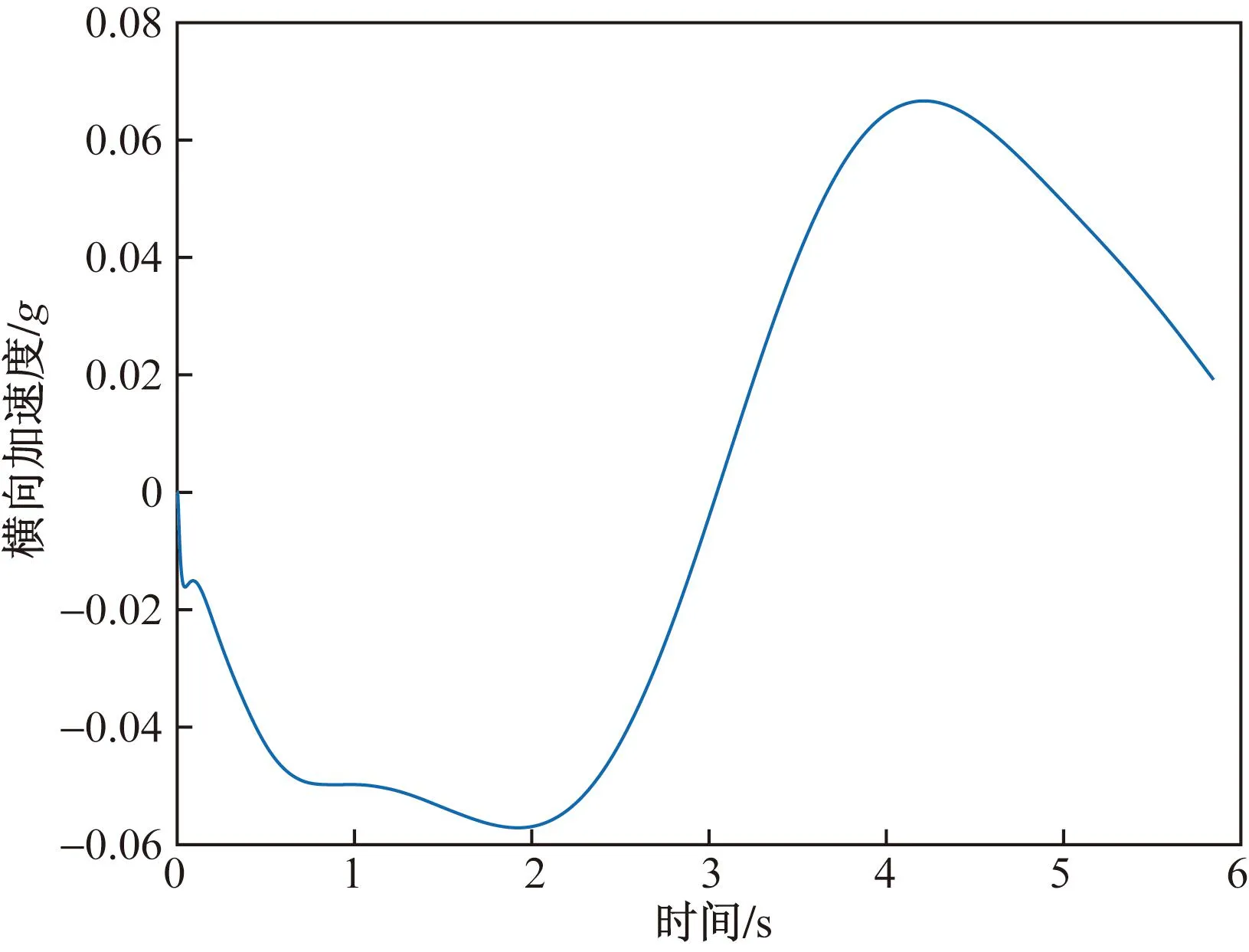
圖13 右側(cè)避障過程中的橫向加速度變化

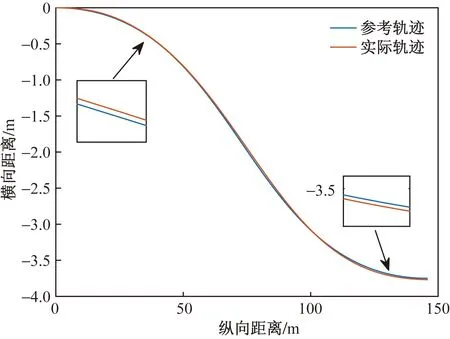
圖14 右側(cè)避障軌跡的跟蹤效果

5 結(jié)論

通過仿真結(jié)果可以得出以下結(jié)論。

(1)貨車在前方出現(xiàn)突發(fā)情況下,采用根據(jù)人的經(jīng)驗建立的模糊策略生成的決策,可以有效地應(yīng)對多車環(huán)境下的緊急轉(zhuǎn)向是向左側(cè)還是右側(cè)轉(zhuǎn)向避障的問題,避免了可能與目標(biāo)車道行駛車輛碰撞的風(fēng)險,提高了貨車在緊急轉(zhuǎn)向時的安全性。

(2)然后根據(jù)在轉(zhuǎn)向初始時自車不同的速度,規(guī)劃出該速度下最合適的三階貝塞爾局部避障曲線,經(jīng)過規(guī)劃軌跡和實際軌跡的對比,該規(guī)劃軌跡可以讓貨車較好地跟蹤,從而實現(xiàn)躲避障礙物。

(3)通過兩次仿真得出的不同速度下轉(zhuǎn)向時的最大橫向加速度均小于規(guī)劃軌跡的最大橫向加速度,滿足在緊急轉(zhuǎn)向時減小貨車側(cè)翻的風(fēng)險的目的。