基于TOF和自適應抗差卡爾曼濾波的UWB室內(nèi)定位算法

方賢寶，林 勇，蘇羿安，鐘樂天

（合肥工業(yè)大學電氣與自動化學院，安徽 合肥 230009）

0 引 言

隨著移動通信、人工智能（AI）的蓬勃發(fā)展，定位技術早已走進人們的日常生活中，如室外定位技術中，全球定位系統(tǒng)（global positioning system，GPS）幾乎覆蓋人類的生產(chǎn)生活。與此同時，人們對室內(nèi)定位的需求也與日俱增，工廠的智能生產(chǎn)、醫(yī)院的高效救治、商場的貨品搜尋等都需要準確的位置定位信息［1］。因此，將位置服務拓展到室內(nèi)是一個急需解決的問題。超寬帶脈沖（impulse radio of ultrawideband，IR-UWB）技術具有高帶寬、高分辨率、高無線傳輸速率、超強魯棒性、低能耗等顯著優(yōu)點，現(xiàn)已成為未來最具開發(fā)前景的室內(nèi)無線定位解決方案之一［2］。常見的超寬帶（UWB）定位技術分為4 類：基于飛行時間（time of flight，TOF）的［3］、基于到達時間差（time difference of arrival，TDOA）的［4］，基于到達角（angle of arrival，AOA）的［5］和基于接收信號強度（received signal strength，RSS）的［6］。但在復雜的室內(nèi)環(huán)境下，UWB 信號傳播極易受到影響，從而造成定位精度降低。文獻［7］使用Chan算法獲取初始定位，比較殘差與門限值鑒別與剔除非視距（non-line-of-sight，NLOS）誤差，再利用改進無跡卡爾曼濾波（unscented Kalman fitering，UKF）算法得到精確的位置坐標；文獻［8］提出對原始定位數(shù)據(jù)進行2 次粒子濾波，通過模型存儲與權重調節(jié)，從而實現(xiàn)精準高效的動態(tài)目標定位；文獻［9］利用抗差因子鑒別NLOS 誤差，以削弱其對測距器造成的噪聲干擾及影響，同時利用Sage-Husa 濾波算法進行估計和校正，最終使用卡爾曼濾波（Kalman filtering，KF）算法實現(xiàn)高精度UWB定位與解算。

造成UWB室內(nèi)定位算法的誤差為標準時間誤差和多徑效應，即在NLOS 環(huán)境下將大大降低定位誤差。而上述文獻只關注于消除NLOS誤差，而忽略了標準時間誤差，所以為了抑制標準誤差和NLOS誤差，提高定位算法的精度，本文提出一種基于TOF 和自適應抗差KF（adaptive robust KF，ARKF）的UWB 室內(nèi)定位算法--IKF 算法。首先對UWB設備進行標定，實現(xiàn)對測距誤差信息的快速修正；針對標準誤差，使用改進的測距算法，優(yōu)化定位；其次采用自適應抗差濾波算法抑制NLOS誤差，提高定位精度。

1 UWB／TOF測距原理

1.1 UWB定位誤差模型

UWB室內(nèi)定位系統(tǒng)如圖1（a）所示，主要由3個主從基站，1個標簽以及路由器和服務器組成。室內(nèi)定位系統(tǒng)中，基站與標簽之間形成的信號直射傳輸路徑往往容易受到室內(nèi)裝飾物或人員等障礙物阻擋，對此產(chǎn)生的信號誤差一般可稱為NLOS誤差，信號的傳播可以稱為NLOS 傳播，路徑軌跡如圖1（b）所示。

圖1 UWB定位模型

假設在視距（line of sight，LOS）環(huán)境下，基站k與標簽在ti時刻測量距離值為rk（ti），具體可表示為

式中Lk（ti）為基站k與標簽在ti時刻的真實距離，nk（ti）為標準時間誤差，由標準時間偏差帶來的測量誤差，包括脈沖信號在基站與標簽之間的固定延時誤差、器件誤差，還與信號傳播距離、室內(nèi)溫度等有關［10］。該類誤差通常認為是均值誤差為0，標準差較小的高斯隨機噪聲，可使用測距標定法消除部分，同時本文使用改進的測距算法進一步剔除，增加定位精度。在NLOS環(huán)境下，存在隨機測量誤差，誤差模型表示為

式中 NLOSk（ti）為NLOS誤差，服從指數(shù)、均勻、高斯或者δ分布，且與系統(tǒng)定位環(huán)境有關，可通過濾波算法降低其誤差。

1.2 TOF測距原理

基于TOF 的測距原理為設備間互發(fā)信號，通過信號TOF與傳播速度測量兩者之間的距離。其方式主要有2種：單邊雙向測距（single-sided two-way ranging，SS-TWR）算法［11］與雙邊雙向測距（double-sided two-way ranging，DS-TWR）算法［12］。

SS-TWR算法原理如圖2（a）所示，先由設備A 向設備B發(fā)送測距請求，當設備B 接收該請求后，延遲一段時間Treply向設備A發(fā)送確認消息，經(jīng)過Tprop設備A 接收。從設備A發(fā)送信息至接收，整個過程時間記為Tround。每個設備都對信號傳輸和接收的時間進行精確記錄，最終計算出Tround和Treply，估算出最終的TOF，測量值與誤差表達式如下

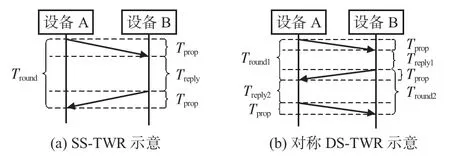
圖2 TOF測距原理

其中，eA與eB為設備A和設備B 的時鐘漂移，單位為10-6。該算法雖僅需一次信息交換即可得到測距信息從而降低功耗，但是TOF 估計誤差隨著Treply的增加而增加，令測距值存在較大誤差，故SS-TWR 算法在實際情形下并不適用。

DS-TWR算法原理如圖2（b）所示。設備A 發(fā)送UWB信號，經(jīng)過Tprop后，設備B 接收并延遲一段時間Treply1后發(fā)送確認消息幀，設備A在接收后延后時間Treply2再次發(fā)送測距信息。最終TOF與估計誤差如下

由式（5）可知，只有令設備的回復時間間隔一致，才可以降低由時鐘漂移引起的標準誤差。該算法雖降低了標準時間誤差，但設備延遲時間必須盡可能相等，若不等，則將增大測距誤差，進一步降低定位精度。

2 算法改進

2.1 基于對稱DS-TWR方法的優(yōu)化

由以上分析可知，SS-TWR算法僅需一次信息交換即可得TOF，但是誤差大，DS-TWR 算法簡單，僅需簡單數(shù)學運算即可得到測距結果，但要求設備高精度，否則將引起較大誤差。對此，本文提出一種基于DS-TWR 的改進算法，如圖3所示。

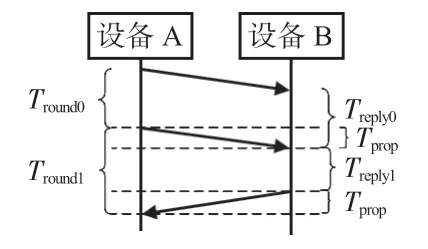
圖3 DS-TWR優(yōu)化算法示意

首先由設備A 發(fā)送測距請求信號，在等待時間Tround0后，再次發(fā)送測距請求，經(jīng)過延遲時間Treply1與信號Tprop后，設備A接收到確認消息幀，其中，Tround0與Treply1為預先設定好的時間間隔。設備B第一次與第二次接收消息的時間間隔設為Treply0，且令其等于Tround0。Tround0和Tround1通過設備計時器得到，通過簡單運算，有

真實值為

由以上公式可得該算法中測量值與真實值Tprop的誤差為

由上式可知，該算法中測距誤差僅與飛行實際時間Tprop和eB有關。由于SS-TWR算法誤差較大，并不適用，僅對比DS-TWR算法與本文改進算法。例如，對于DS-TWR算法，假設當設備A與設備B應答消息延遲時間相差1 ms、時鐘漂移之差為2 ×10-5，真實距離為300 m 時，計算出標準誤差為5 ns，對此產(chǎn)生的測距誤差為1.5 m；而本文測距算法中，信號傳播時間的實際值為1 000 ns，當設備B 的時鐘漂移eB最大為20 ×10-6，TOF誤差僅為0.04 ns，測距誤差為1.2 cm。相比DS-TWR 算法，該算法降低了標準時間誤差，提升了測距精度。

2.2 基于KF算法的優(yōu)化

KF是一種線性濾波器，可以根據(jù)上一時刻的系統(tǒng)狀態(tài)和預測狀態(tài)，對系統(tǒng)下一時刻的真實狀態(tài)進行推測的最優(yōu)估計算法［13］。KF 本身是一種遞歸過程，由以下5 個遞歸方程組成

式中Ak-1與Bk-1分別為狀態(tài)轉移矩陣和輸入控制矩陣，Qk-1為過程噪聲協(xié)方差矩陣，Uk-1為系統(tǒng)控制量，Hk為觀測模型矩陣，Rk為過程噪聲協(xié)方差矩陣。Kk為卡爾曼增益，對最優(yōu)估計＾Xk進行比例調節(jié)，其大小反映了在最優(yōu)化狀態(tài)值估計過程中“更相信”觀測值Zk還是估計值。

KF算法能夠對數(shù)據(jù)進行線性濾波，結合觀測值與測量值，最終得到系統(tǒng)的最佳估計值。但在復雜的室內(nèi)環(huán)境下，室內(nèi)裝飾與人員等都會遮擋UWB 信號，形成多徑效應，帶來NLOS誤差，使得定位估計值出現(xiàn)偏差。因此，本文提出抗NLOS KF算法，通過比較殘差與3 倍信息的方差來判斷LOS與NLOS情形，若存在NLOS則對增益進行縮放以減小測距誤差。

測量的部分異常值是在k時刻的最優(yōu)估計時首次被引入，若能預先將計算所得的殘差進行修正，再繼續(xù)進行濾波最優(yōu)估計，則可以有效消除部分異常值，將殘差矩陣Δk和方差矩陣Dk定義為

依據(jù)3倍方差理論和上式，得到如下判斷公式

式中為Dk矩陣對角線上的第i個元素，為Δk的第i個元素，當上式不滿足時，則受到NLOS誤差，進行修正

式中α為修正系數(shù)，決定了對NLOS誤差的抑制效果。在實際情形中，UWB使用場景受到的NLOS誤差不是唯一的，因此對α取固定值不符合實際。所以，為進一步提高抗NLOS誤差的效果，需要依據(jù)殘差與方差的對應關系來調節(jié)α的值

其中，b為調制指數(shù)，控制著修正指數(shù)的放大與縮小。當處于移動情形下，定位精度會受到NLOS 誤差而發(fā)生變化，相對應的殘差也會改變，所以需要調節(jié)修正系數(shù)α在1 -b至1不斷變化，達到自適應抗NLOS 誤差的效果。在本文中，最終經(jīng)過實驗驗證，修正系數(shù)α設為0.8，最大縮小比例b設置為0.4可達到最佳實驗效果。

3 實驗與驗證結果

實驗布置如圖4所示。圖4中，標簽位于Pi處，基站分布四周，分別使用KF算法和本文算法進行濾波，最后使用三邊定位法進行定位，使用式（16）計算定位誤差，比較定位精度

圖4 實驗環(huán)境示意

其中，（x，y）為定位算法解算得到的標簽坐標，（xt，yt）為標簽實際坐標。

3.1 UWB測距標定

為進一步消除定位誤差，本文實驗依次對實驗設備進行測距標定［14］。實驗在逸夫樓4 樓一個空實驗室內(nèi)進行，大小為6.5 m×8 m，實驗環(huán)境中基站與標簽之間無遮擋物，無實驗人員穿行，為相對意義下的LOS環(huán)境。首先對基站A1 進行測距實驗標定：基站A1 不動，標簽由近及遠選擇10個待測點，通過測距儀器測得的距離作為真實值，標簽與基站A1測得的數(shù)據(jù)在使用3σ原則剔除較大誤差數(shù)據(jù)后取平均值作為量測值，對2種測量數(shù)據(jù)進行一次線性擬合，確定誤差模型，完成基站的標定，其余基站同理。表1 為UWB各基站的校正參數(shù)。其中，擬合優(yōu)度的數(shù)值越接近1，表明擬合程度越好。

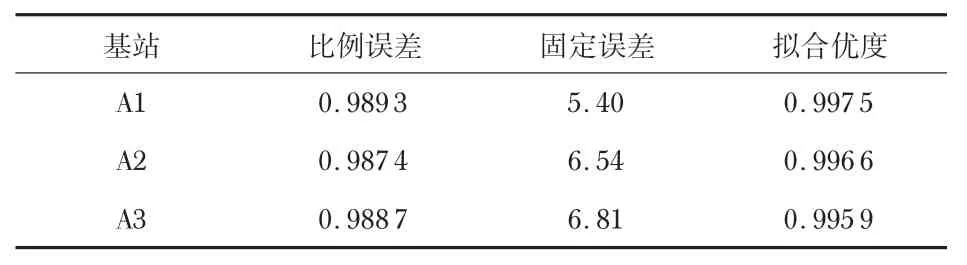
表1 基站校正參數(shù)

3.2 UWB靜態(tài)定位實驗

表2列出了LOS環(huán)境下，2 種算法在靜態(tài)時定位誤差的數(shù)據(jù)對比。可以看出，在觀測環(huán)境較好的情形下，2 種算法的精度相當，但IKF 算法精度仍有較小的提高。因為本文使用了改進的TOF算法和測距標定，剔除了標準誤差，一定程度上提高了定位精度。

表2 靜態(tài)測試點LOS環(huán)境定位誤差比較

表3為在NLOS環(huán)境下的靜態(tài)定位實驗結果。可以看到：KF算法的最小誤差達到約30 cm，而IKF算法最大誤差僅為20 cm左右，平均定位誤差大幅度降低。整體上，本文提出的算法可以在NLOS環(huán)境下有效且準確地對系統(tǒng)進行靜態(tài)定位。

表3 靜態(tài)測試點NLOS環(huán)境定位誤差比較

3.3 UWB動態(tài)定位實驗

在本文實驗中，實驗人員攜帶標簽從P1 出發(fā)，依次經(jīng)過P2，P3，P4，P5，直至點P6，整體呈現(xiàn)5 字型，進行LOS與NLOS環(huán)境下的動態(tài)定位實驗，人員以正常勻速移動。如圖5 所示，ARKF 算法與KF 算法在2 種環(huán)境下的定位軌跡。

圖5 2 種算法在LOS環(huán)境下的動態(tài)定位比較

從圖5中的2幅圖對比看出，在LOS環(huán)境下，2 種算法的動態(tài)定位結果相差不大，但KF算法仍有較少部分的斷點與軌跡偏移，而本文算法基本貼合原路徑。在NLOS 環(huán)境下，如圖6 所示，KF 與ARKF 算法皆有一定的誤差，但KF算法卻有部分斷點，偏離原路徑，最大誤差達到50 cm，而本文算法動態(tài)定位較連續(xù)，無較大偏差，可以達到20 cm以內(nèi)，最大誤差僅25 cm，定位效果較好，定位精度較高。

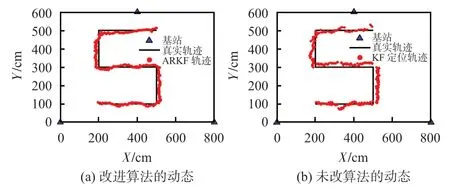
圖6 2 種算法在NLOS環(huán)境下的動態(tài)定位比較

4 結束語

在UWB測距過程中，易受包括器件誤差、延時誤差在內(nèi)的標準誤差以及NLOS 測距誤差等因素的影響，導致測距精度大幅度降低。針對前者，本文提出一種改進的TOF算法，并對設備進行測距標定，利用一次線性擬合剔除測距過程中的標準誤差；通過比較殘差與3 倍信息的方差判斷是否有NLOS存在，以此減小NLOS 誤差。實驗結果表明：本文提出的改進算法能夠有效剔除標準時間誤差與NLOS誤差，提高定位系統(tǒng)在復雜室內(nèi)環(huán)境下的定位精度。