ENTIRE SOLUTIONS OF HIGHER ORDER DIFFERENTIAL EQUATIONS WITH ENTIRE COEFFICIENTS HAVING THE SAME ORDER*
(馮子恒) (黃志波)
School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China E-mail: 2020021880@m.scnu.edu.cn; huangzhibo@scnu.edu.cn
Yezhou LI (李葉舟)?
School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China E-mail: yezhouli@bupt.edu.cn
Abstract In this paper, we consider entire solutions of higher order homogeneous differential equations with the entire coefficients having the same order, and prove that the entire solutions are of infinite lower order.The properties on the radial distribution, the limit direction of the Julia set and the existence of a Baker wandering domain of the entire solutions are also discussed.
Key words entire solutions;radial order;Julia limiting direction;Baker wandering domain;transcendental direction
1 Introduction
We assume that the reader is familiar with the fundamental results and the standard notations of Nevanlinna’s value distribution of meromorphic functions (see [9, 14, 24, 30]).For a meromorphic functionf(z) in the complex plane C, the orderρ(f) and the lower orderμ(f)are defined by, respectively,
Iffis entire function,then the Nevanlinna characteristicT(r,f)can be replaced with logM(r,f),whereM(r,f) = max{|f(z)| :|z|≤r}.Leta ∈C andn(r,f=a) denote the numbers off(z)-a=0 in disk{z:|z|≤r}.If
thenais called the Borel exceptional value off.
This paper is devoted to considering the properties, such as the growth order, the radial oscillation and limiting direction of Julia sets, and the existence of a Baker wandering domain,of solutions to higher order linear differential equations
whereAj(z) (j=0,1,2,···,k-1) are entire functions.Due to the classical result by Wittich[23], all solutions to (1.1) are entire functions with finite order if and only if all coefficients are polynomials.If max{ρ(Aj),j=1,2,···,k-1}<ρ(A0), then every non-trivial solution to(1.1) is of infinite order.Furthermore, if the coefficients have the properties on the Phragm′en-Lindel¨of indicator function,every non-trivial solution to(1.1)is also of infinite order[10].In this paper, we concentrate on looking at the situation when the coefficients of (1.1) are exponential polynomials with the same degree, that is, all coefficients have the same order.
2 Radial Distribution of Entire Solutions

We first recall Nevanlinna’s Characteristic in an angle (see [29]).Assumeing that 0<α <β <2π, we denote that Clearly,I(g) is closed, so it is measurable.We use mesI(g) for the linear measure ofI(g).For instance, mesI(g)=πwheng(z)=exp{ez}.
A natural question that arises is: what is the lower boundary of mesI(g) when the entire functiong(z) is of infinite order? The radial distribution of transcendental entire solutions has been well studied, for instance, see [13, 16, 18, 25].We now recall Huang and Wang’s result on the differential equation.
Theorem 2.1([13, Theorem 1.3]) Suppose thatA(z) andB(z) are entire functions withμ(B)>ρ(A).Ifg(z) is a non-trivial solution of the equation
then mesI(g)≥min{2π,π/μ(B)}.
Theorem 2.1 tells us that mesI(g)=2πwhenμ(B)≤1/2.Furthermore, we also note that equation(2.1)and all other previous results have dominated coefficients.Now,we consider that all entire coefficients have the same order and obtain
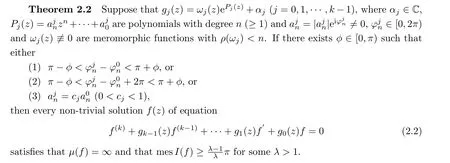
Before proceeding to the actual proof of Theorem 2.2, we introduce some lemmas.
Lemma 2.3([8, Theorem 2]) Letf(z) be a transcendental meromorphic function and letα >1 be a real constant.Then there exists a setE ?[0,2π) that has linear measure of zero, and there exists a constantB >0 such that ifθ ∈[0,2π)E, then there exists a constantR0=R0(θ)>1 such that, for allzsatisfying argz=θand|z|=r >R0, we have that
Lemma 2.4([15]) Suppose thatP(z) = (α+iβ)zn+··· is a non-constant polynomial with degreen ≥1, thatα,βare real constants, and thatω(z)/≡0 is a meromorphic function withρ(ω)<n.Setg(z) =ω(z)eP(z),z=reiθ, andδ(P,θ) =αcosnθ-βsinnθ.Then, for any givenε >0, there exists a setH1?[0,2π) of linear measure of zero such that, for anyθ ∈[0,2π)(H1∪H2) and|z|=r >r0(θ,ε), we have that
(i) ifδ(P,θ)>0, then exp{(1-ε)δ(P,θ)rn}<|g(reiθ)|<exp{(1+ε)δ(P,θ)rn};
(ii) ifδ(P,θ)<0, then exp{(1+ε)δ(P,θ)rn}<|g(reiθ)|<exp{(1-ε)δ(P,θ)rn},whereH2={θ ∈[0,2π):δ(P,θ)=0}.
Remark 2.5As described in Lemma 2.4,
(i) if we set thatα+iβ=an=|an|eiφn, then we have thatδ(P,θ)=|an|cos(φn+nθ);

whereE1is a set of linear measure zero andBis a positive constant.
By Lemma 2.4 and Remark 2.5, there exists a setH0={θ ∈[0,2π) :δ(P0,θ)>0}such that, for allzsatisfying that argz=θ ∈H=H0E1, one of the following statements holds:
(a)δ(Pj,θ)<0 (j= 1,2,···,k- 1) for some properφandθ ∈H3when one of the conditions (1) or (2) holds, whereH3is a subset ofHwith a positive linear measure;


for allz ∈Ω(αi+2γ,βi-2γ) outside anR-setD.

3 Limiting Direction on Julia Sets of Entire Solutions


Recently, Wang et al.[21] investigated the limiting direction and transcendental direction of transcendental entire solutions of complex differential equations, and obtained
Theorem 3.1([21, Theorem 1.3]) Suppose thatsandmare integers,F(z) is a transcendental entire function of finite lower order, and thatP(z,f) is a differential polynomial infwithγP ≥s, where all coefficientsaj(z) (j= 1,2,···,l) are polynomials ifμ(F) = 0, or allaj(z) (j= 1,2,···,l) are entire functions withρ(aj)<μ(F) ifμ(F)>0.Then, for every non-zero transcendental entire solutionfof the differential equation
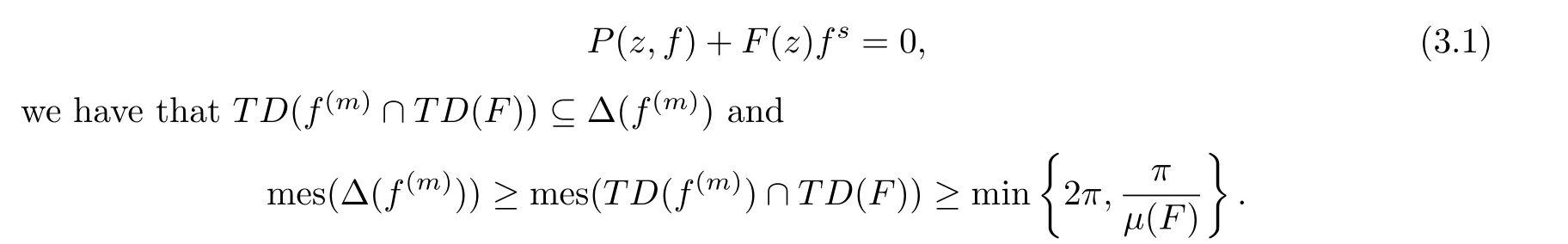
We now consider the higher order homogeneous differential equations (2.2) with entire coefficients having the same order, and obtain
Theorem 3.2Letm ∈Z.Suppose that the entire coefficientsgj(z) (j=0,1,···,k-1)of equation (2.2) satisfy the conditions given in Theorem 2.2.Then every non-trivial solutionf(z) of equation (2.2) satisfies that
Before proving Theorem 3.2, we introduce some preliminary lemmas.
Lemma 3.3([5]) Letf(z) be a transcendental meormorphic function with finite lower orderμand have a positive deficiency
Let Λ(r) be a positive function such that Λ(r) =o(T(r,f)) asr →∞, and letDΛ(r) ={θ ∈[0,2π) :|f(reiθ)|>eΛ(r)}.Then, for any fixed sequence of P′olya peaks{rn}of orderμ, we have that
Lemma 3.4([21]) Letf(z) be a transcendental meromorphic function with finite lower orderμandδ(∞,f)>0, and let Λ(r) be a positive function such that Λ(r) =o(T(r,f)) and Λ(r)/logr →∞asr →∞.Then
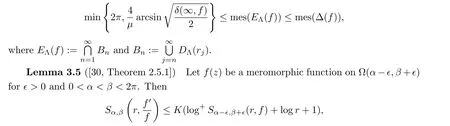
whereK >0 andr >1, possibly except for a set with a finite linear measure.
Lemma 3.6Letf(z) be transcendental entire function, and letm ∈Z.ThenTD(f)?TD(f(m)).
ProofBy Lemma 2.9 in[21],we just need to prove that the conclusion holds whenm <0.For any givenθ/∈TD(f(m)), it follows from the definition of the transcendental direction that there exist∈>0 andK0>0 such that, for allz=reiθ ∈Ω(θ-∈,θ+∈),

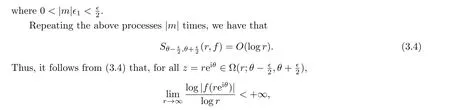
which implies thatθ/∈TD(f).HenceTD(f)?TD(f(m)).□
We now proceed to the proof of Theorem 3.2.
Proof of Theorem 3.2Sincem ∈Z, we will spilt our proof into two cases.
Case 1m=0.

Case 2m/=0.
It follows from Lemma 3.6 and the proof of Case 1 thatTD(f)∩TD(g0)?TD(f(m))∩TD(g0).Thus
4 Baker Wandering Domain of Entire Solutions
LetUbe a connected component ofF(f).Thenfn(U) is contained in a component ofF(f), denoted byUn.If, for some integerp ≥1,fp(U)?Up=U, thenUis called a periodic component ofF(f), such the smallest integerpis the period of the periodic componentU.If,for somen,Unis periodic butUis not periodic, thenUis called pre-periodic.Uis called a wandering domain if it is neither periodic nor pre-periodic, that is,Un/=Umfor alln/=m.IfUis wandering and allUnare multiply-connected and surround 0, and the Euclidean distance is dist(0,Un)→∞asn →∞, thenUis called the Baker wandering domain.By Sullivan’s famous theorem, rational functions have no wandering domains.For a transcendental entire function, it has been shown by Baker[3]that such domains may exist; each multiply-connected component ofF(f) must be a Baker wandering domain (see [2, 7, 28, 29]).There are some criteria of non-existence for the Baker wandering domains [4, 7], which also determine whether there exists only a simply connected Fatou component for given entire functions.
As is well all known, the properties of solutions of differential equations are always controlled by the behavior of coefficients.When there is a dominated coefficientg0in the sense thatT(r,gj) =o(T(r,g0)) (j= 1,2,···,k-1) asr →∞, the dynamical properties of differential equations (3.2) have been investigated in [11, 12, 20].However, we are interested in the dynamical properties of solutions of differential equations(2.2)without the dominated coefficient,that is, where all coefficients are of the same growth order.Wang and Chen[20]considered the second order differential equation and obtained
Theorem 4.1([20, Theorem 1.2]) Suppose thatBj(j= 1,2) are constants and thatAj(z)(j=1,2)are entire functions,and thatPj(z)=ajzkj+··· (j=1,2)are two polynomials of degreekj ≥0.Suppose that any one of the following two conditions holds:
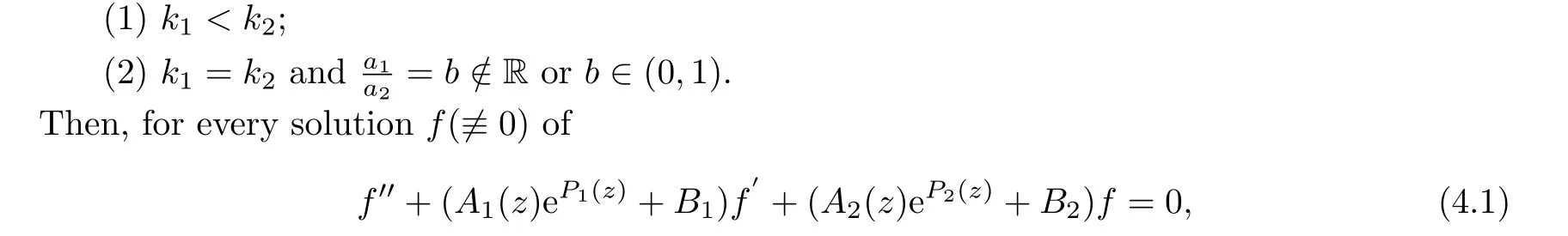
allf(n)(n ∈Z) have no Baker wandering domain, that is, they only have a simply connected Fatou component.
We focus our interest on the higher differential equations (2.2) with coefficients having the same order and obtian
Theorem 4.2Suppose that the entire coefficientsgj(z) (j=0,1,···,k-1) of equation(2.2) satisfy the conditions given in Theorem 2.2.Then, for every non-trivial solutionf(z) of equation (2.2),f(m)(z)(m ∈Z) have no Baker wandering domain, that is, they only have a simply connected Fatou component.
We now present some Lemmas.
Lemma 4.3([28, Corollary 1]) Letf(z) be a transcendental meromorphic function with at most finitely many poles.IfJ(f) has only bounded components, then for any complex numbera ∈C, there exists a constant 0<d <1 and two sequences{rn}and{Rn}of positive numbers withrn →∞andRn/rn →∞(n →∞) such that
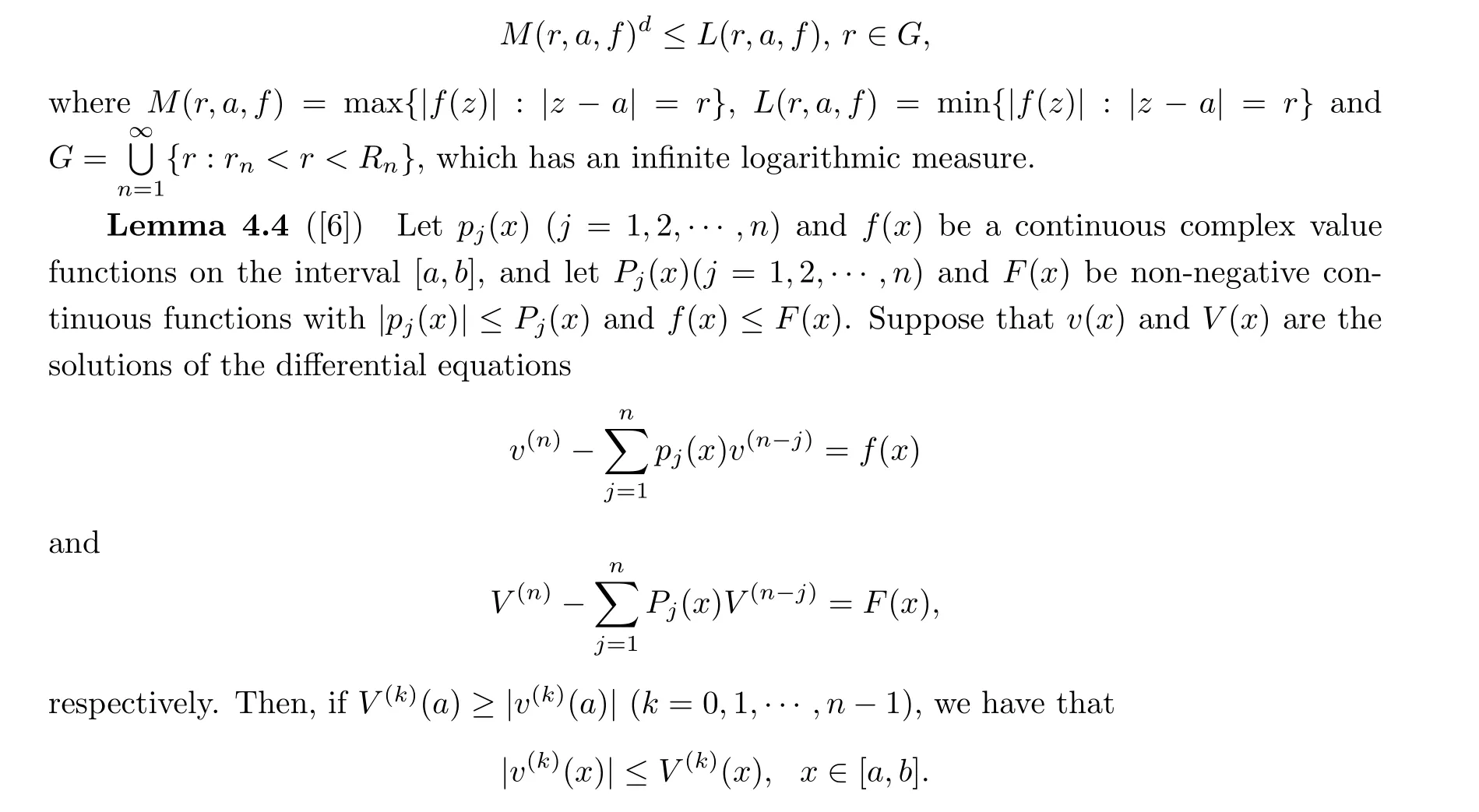
We now proceed to the actual proof of Theorem 4.2.
ProofWe now assume thatu(z) =f(m)(z) (m ∈Z) has a Baker wandering domain,and complete the proof by reduction to absurdity.Zheng [27] shows that the Julia set of a transcendental meromorphic function with at most finitely many poles has only bounded components if and only if it has a Baker wandering domain.Sinceuis a transcendental entire function,J(u) has only bounded components.Thus, it follows from Lemma 4.3 that there exists 0<d <1 such that

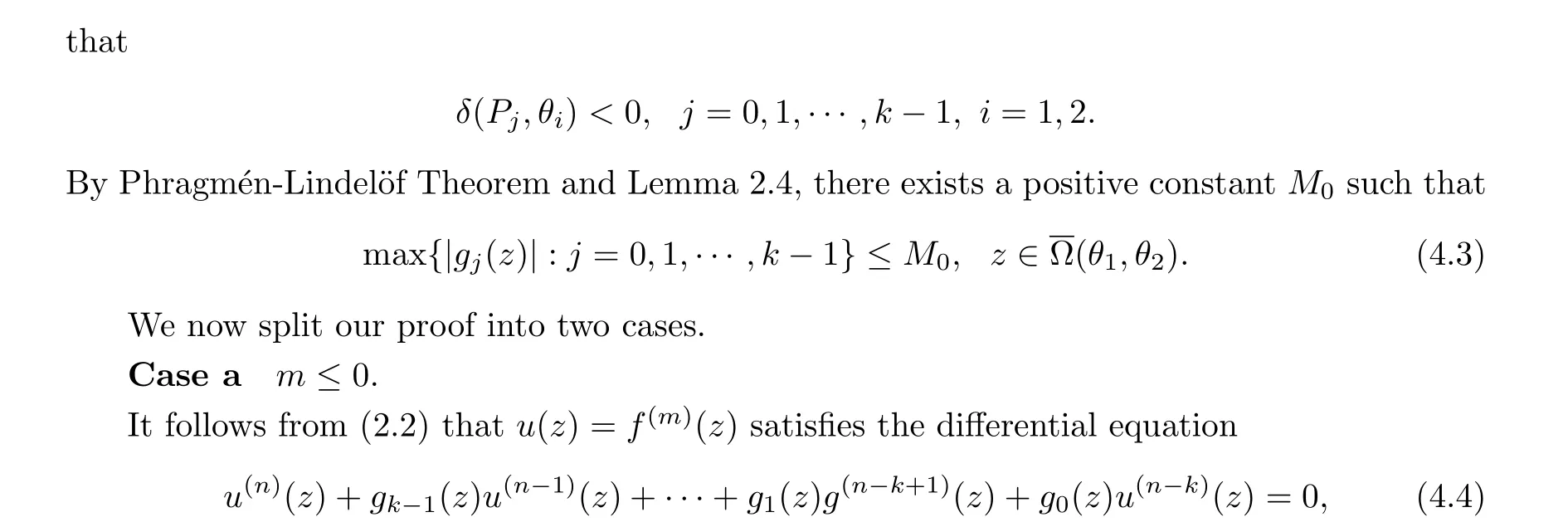
wheren=-m+k.
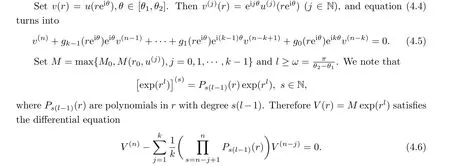
Clearly,|v(j)(r0)| =|eijθu(j)(reiθ)|≤V(j)(r0),j ∈N.Thus, we conclude from Lemma 4.4,(4.5) and (4.6) that, for sufficiently larger0andr ≥r0,
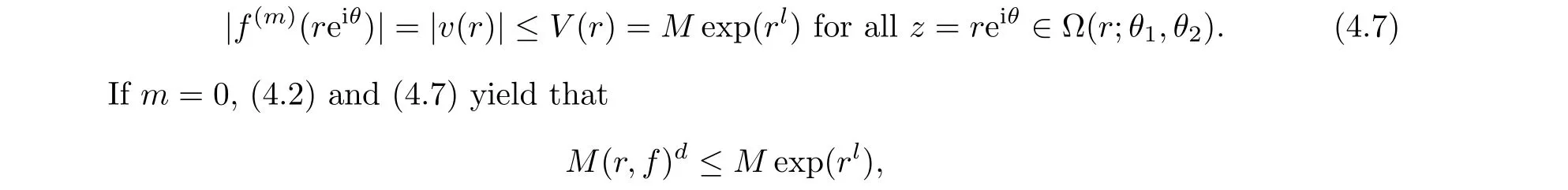
which implies thatμ(f)≤l, which contradicts to Lemma 2.6.
Sincefis entire function, we have thatCθ1,θ2(r,fm) = 0 =Cθ1,θ2(r,u) = 0.Thus, we obtain from (4.2) and (4.7) that, for allr ≥r0andm ≤0,
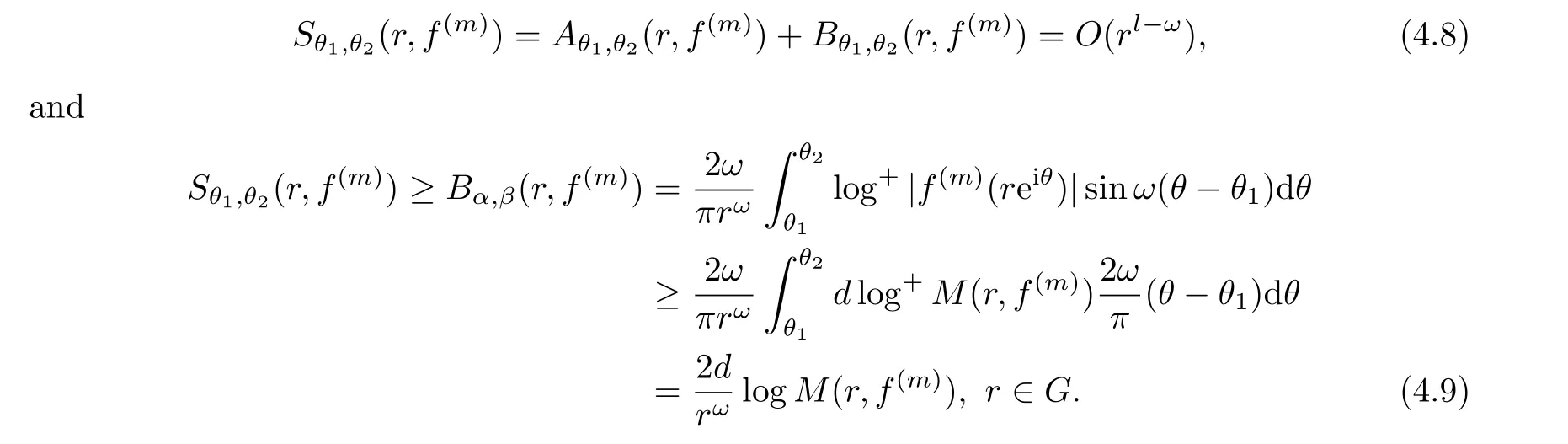
Clearly, (4.8)and(4.9)imply thatμ(f)=μ(f(m))<∞, which again contradicts to Lemma 2.6.
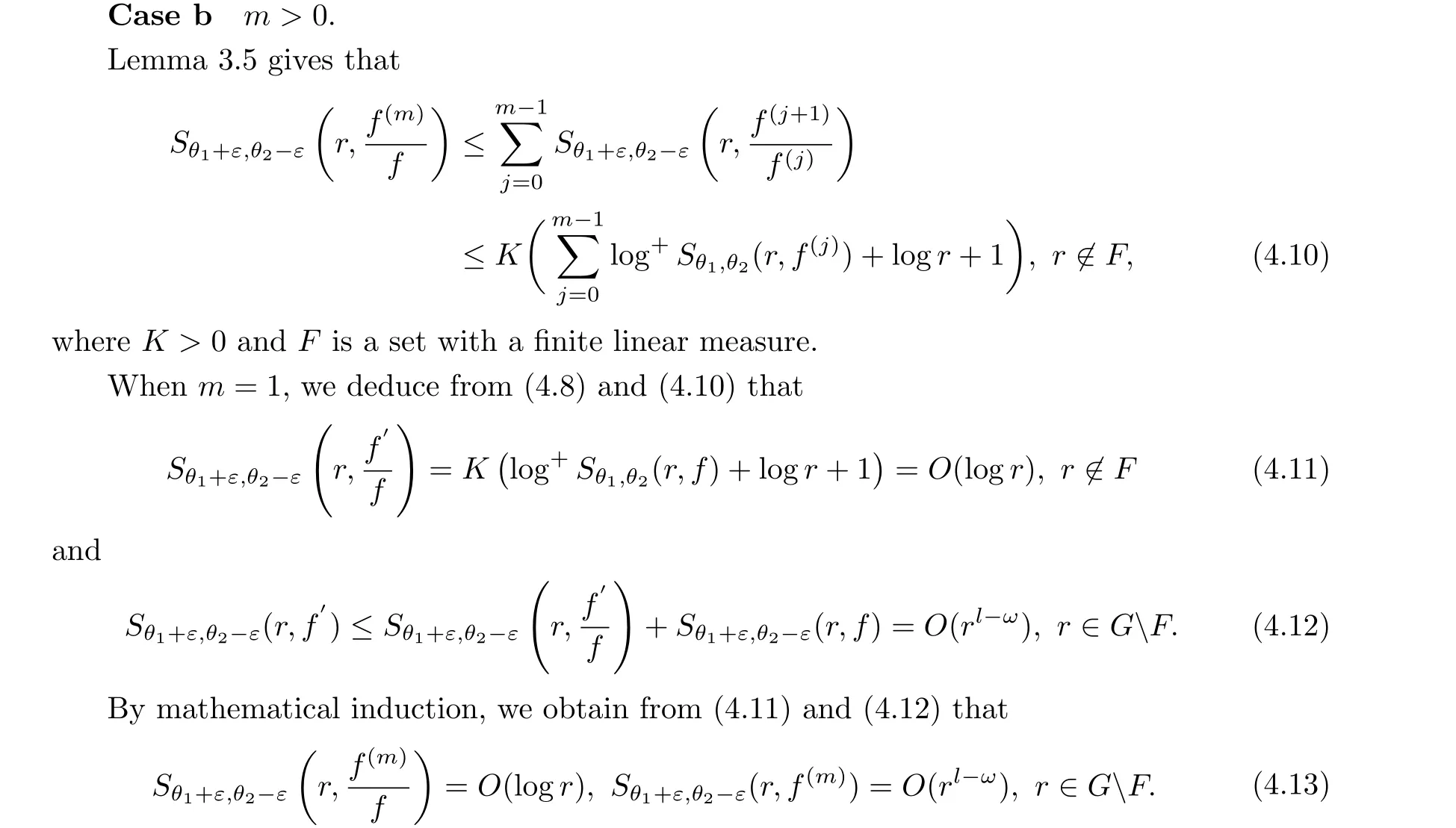
Thus, we deduce from (4.2) and (4.13) that, forr ≥r0andm >0,
Obviously, (4.13) and (4.14) yield thatμ(f)=μ(f(m))<∞, which contradicts to Lemma 2.6.
Thus, Cases a and b imply that, for every non-trivial solutionf(z) of equation (2.2),f(m)(z)(m ∈Z) have no Baker wandering domain.That is, they only have a simply connected Fatou component.□
Conflict of InterestThe authors declare no conflict of interest.
 Acta Mathematica Scientia(English Series)2024年1期
Acta Mathematica Scientia(English Series)2024年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*
- THE BOUNDEDNESS OF OPERATORS ON WEIGHTED MULTI-PARAMETER LOCAL HARDY SPACES*
- AGGREGATE SPECIAL FUNCTIONS TO APPROXIMATE PERMUTING TRI-HOMOMORPHISMS AND PERMUTING TRI-DERIVATIONS ASSOCIATED WITH A TRI-ADDITIVE ψ-FUNCTIONAL INEQUALITY IN BANACH ALGEBRAS*
- INTERFACE BEHAVIOR AND DECAY RATES OF COMPRESSIBLE NAVIER-STOKES SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND A VACUUM*
- CONVEXITY OF THE FREE BOUNDARY FOR AN AXISYMMETRIC INCOMPRESSIBLE IMPINGING JET*
- SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*
