EMCA:一種新的多云存儲中高效的多副本審計方案
胡雨晴,金 瑜
(1.武漢科技大學 計算機科學與技術學院,湖北 武漢 430065;2.湖北省智能信息處理與實時工業重點實驗室,湖北 武漢 430065)
0 引 言
近年來,云存儲[1]得到了廣泛應用,它允許用戶將其海量本地數據,以低廉的價格外包給遠程存儲服務器。然而,云存儲也存在缺點:一旦用戶將其數據外包給不可靠的遠程存儲服務器,且沒有完整的本地備份,用戶的數據就會面臨許多安全威脅,例如,遠程存儲服務器會因為自然或人為事故、黑客攻擊丟失數據,甚至會為了減少維護費用,故意刪除用戶很少使用的數據等等。學術界和工業界已經為解決這個問題付出了大量努力。云數據審計也稱為可證明數據占有(Provable Data Possession,PDP)[2],是數據所有者在不下載數據的情況下檢查數據是否在遠程云服務器上正確存儲的一項重要技術[3]。
盡管PDP可以幫助數據所有者檢查數據完整性,但是一旦數據被破壞,數據所有者也會永遠丟失數據。為了提高數據的持久性和可用性,數據所有者可以生成多個副本,如果一個副本被篡改,數據所有者可以利用其他副本恢復數據。然而,大多數現有方案只考慮檢查單個數據的完整性[4-5],對于多個副本,必須運行N次以檢查N個副本的完整性,這種方案的效率很低。為了克服這個問題,已有學者提出了一些用于多副本的PDP方案[6-7],而上述方案都只考慮了一個簡單的情況,即所有副本都存儲在一個云存儲服務器上,一旦服務器出現故障,用戶仍然面臨數據丟失的風險。且傳統的僅限于單一提供商數據中心的云基礎設施正在不斷發展,多云是下一代云系統的趨勢[8]。因此,設計一種高效的多副本、多云存儲服務器PDP方案是很有意義的。
根據上述多副本方案存在的問題,該文提出了EMCA(Efficient Multi-replica and multi-Cloud Audit),一種新的高效的多副本、多云數據審計方案。EMCA具有以下特性:(1)為多云存儲服務提出了一個安全的數據審計方案,使用第三方審計者(Third Party Auditor,TPA)協助審計,實現了多云情景下的數據完整性驗證。(2)能夠一次驗證不同云服務器上的所有抽樣副本,采用模冪加密技術[9]計算審計結果,實現了高效的多副本批量數據審計。
1 相關工作
1.1 單副本數據審計
Ateniese等人[2]首次提出了PDP的概念,該方案利用基于RSA(Rivest-Shamir-Adleman)的同態驗證標簽(Homomorphic Verifiable Tag,HVT),將生成的標簽聚合為單個值,大大減少了審計過程中的存儲和通信開銷。然而,該方案僅適用于驗證靜態文件。Erway等人[10]擴展了PDP模型,并首次提出了一種完全動態的PDP解決方案,稱為DPDP,然而,該方案的執行效率仍然存在疑問。Wang等人[11]設計了另一種動態PDP方法,使用Merkle哈希樹(Merkle Hash Tree,MHT)支持數據更新。此外,Zhu等人[12]使用索引哈希表(Index Hash Table,IHT)實現了全數據動態的公共審計,大大降低了計算和通信成本。
為了有效支持用戶撤銷,Wang等人[13]提出了Panda,通過使用代理重簽名技術,半可信云服務提供商可以將被撤銷用戶生成的簽名轉移到目標用戶私鑰下。為了實現用戶身份的隱私性,Wang等人[14]提出了第一個針對共享數據的隱私保護公共審計方案,稱為Oruta。此方案將環簽名和HVT相結合,對被質詢塊的簽名進行聚合,實現了簽名者身份保密的目的。此外,Shen等人[15]提出了一種基于身份加密的數據共享方案,簡化了復雜的證書管理。
1.2 多副本數據審計
Curtmola等人[16]提出了一種基于RSA簽名的多副本審計方案,這是首次嘗試創建多個副本并對其進行檢查的方案。通過先加密然后隨機化來生成文件的多個副本,已實現副本的可區分性以及數據隱私。針對證書管理開銷,Zhou等人[17]提出了一個無證書的多副本動態完整性審計方案,通過改進經典MHT實現副本的批量更新,同時提供可變副本數存儲。然而,該方案并不支持多云環境。為了解決這個問題,不少學者提出了多云多副本的審計方案[18-19]。Yang等人[20]提出使用區塊鏈中隨機數的不可預測性來抵制惡意審計員,使用動態哈希表實現多云多副本的審計方案。然而,上述方案[18-20]均采用計算復雜的雙線性配對完成完整性驗證,導致計算成本較高。
基于此,設計一種在多云環境中高效的多副本數據審計方案是很有意義的。該文通過使用模冪加密技術來實現審計,其中最復雜的運算是模冪運算,這只會消耗很少的計算成本,同時,可一次驗證不同云服務器上的所有副本,實現高效的多云多副本審計。
2 具體方案
2.1 預備知識
2.1.1 同態驗證標簽
數據塊的同態可驗證標簽是一種不可偽造的驗證元數據,它具有同態的特征,這是由Ateniese等人首次引入的。HVT的特性如下:
(1)無塊驗證。通過使用HVT,用戶可以在不訪問數據塊的情況下驗證CSP生成的完整性證明。
(2)同態標簽。對于任意兩個數據塊bi和bj以及相應的同態驗證標簽Tag(bi)和Tag(bj),(bi+bj)的HVT可以通過Tag(bi)和Tag(bj)生成。
該文使用以下基于RSA的安全哈希函數來構造HVT。N=pq是一個公共RSA模,其中p=2p'+1和q=2q'+1是兩個足夠大的秘密素數。讓QRN為模N的二次剩余集,g為QRN的生成元。因此,數據塊bi的基于RSA的HVT可以定義為:
Tag(bi)=gbimodN
(1)
HVT的同態特性由以下等式給出:
Tag(bi+bj)=gbi+bjmodN=
(gbimodN)*(gbjmodN)=
Tag(bi)*Tag(bj)
(2)
另外,如果r和bi是兩個足夠大的整數,可以構造以下等式,該等式將用于后續的完整性驗證:
Tag(bi)s=(gbi)smodN=gsbimodN=
(gs)bimodN
(3)
2.1.2 副本記錄表
如表1所示,副本記錄表[20]記錄了文件副本與物理存儲位置的映射關系。表項為文件號、副本號和CSPID,根據文件號和副本號可鎖定唯一副本,根據CSPID可確定該副本的存儲位置。其中,xi表示存儲ID(F)第i個副本的CSP的ID。

表1 副本記錄表
2.2 系統模型
多云多副本的審計系統模型如圖1所示,系統中包含四個實體:用戶(User)、云服務提供商(Cloud Service Provider,CSP)、云服務管理者(Cloud Service Organizer,CSO)和第三方審計者(Third Party Auditor,TPA)。
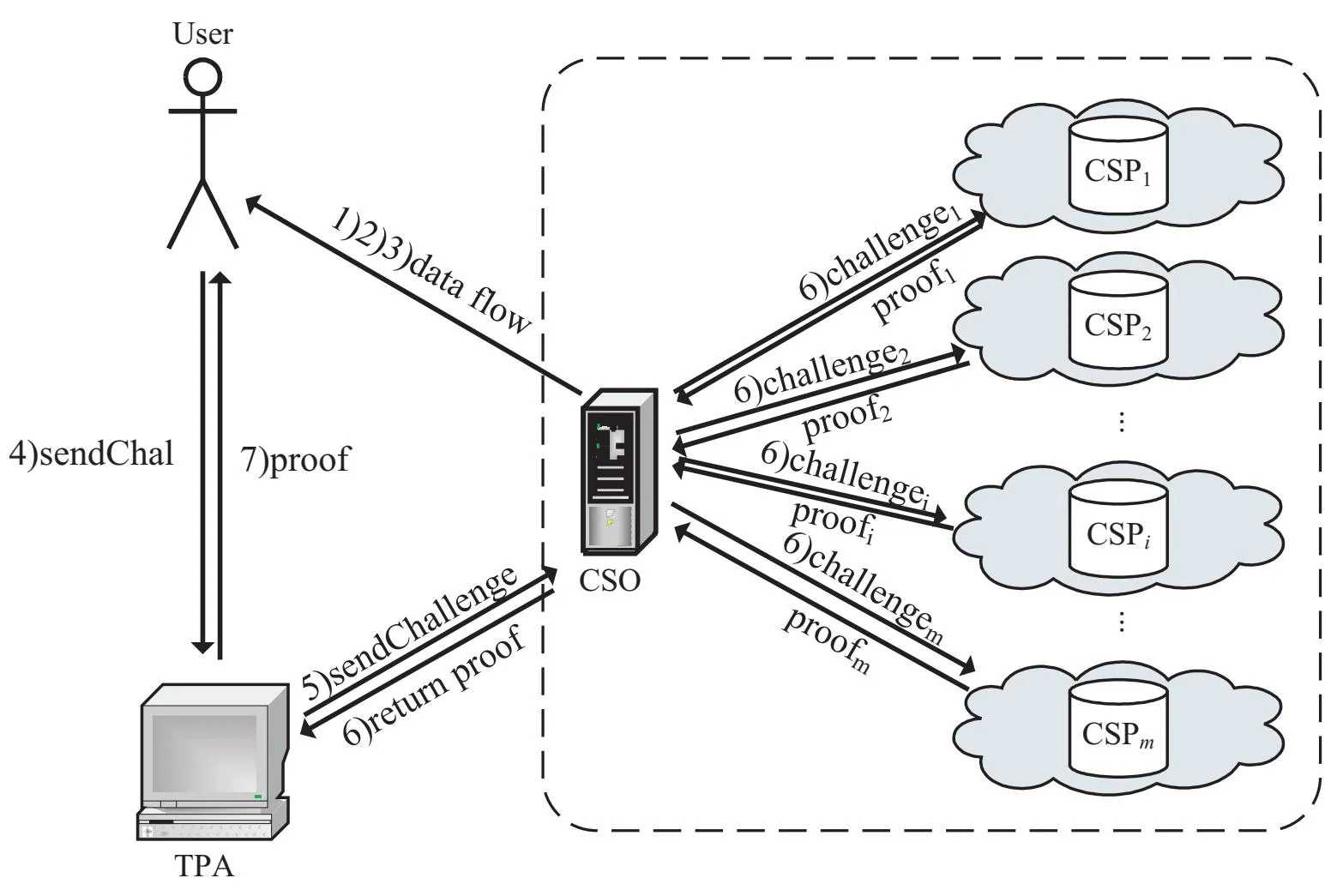
圖1 系統結構
用戶(User)可以是個人或企業,它將數據存儲在多個CSP上,還將檢查外包數據的完整性。
云服務提供商(CSP)為用戶提供網絡存儲和計算服務,但CSP可能會丟失或損壞用戶數據。
云服務管理者(CSO)是一家特殊的云服務提供商,負責在多云環境下管理多個CSP。
第三方審計者(TPA)在用戶的授權下管理或監控外包數據。
方案的大致過程如下:
(1)用戶對數據進行初始化,將文件分塊,并生成副本,將副本發送至CSP存儲。
(2)用戶生成數據標簽并發送至TPA存儲。
(3)CSP驗證收到的數據是否正確。
(4)用戶生成隨機數,發送給TPA。
(5)TPA生成挑戰信息并發送給CSO。
(6)CSO將挑戰信息分派給CSP,CSPi生成證據Proofi,CSO將證據聚合成ProofCSP,并發送給TPA。
(7)TPA收到證據后,根據存儲的標簽計算ProofTPA。TPA將ProofCSP和ProofTPA一同發送給用戶。
(8)用戶利用第四步生成的隨機數審計證據。
2.3 安全性假設
假設用戶和CSO是可信的。
假設CSP是半可信的,惡意或粗心大意的CSP可能會丟失數據,也可能會刪除用戶很少使用的數據以減輕其存儲負擔。
假設TPA是半可信的。TPA可能通過與云服務器串通向用戶隱瞞數據損壞事件。
2.4 關鍵過程
多云多副本的審計系統方案由三部分組成:初始化階段、設置階段和公開審計階段。一些必要的符號定義如表2所示。

表2 相關符號定義
文中的一些密碼變換如下(以k表示密鑰長度):
E(·):{0,1}k×{0,1}*->{0,1}k為對稱加密算法,用戶對文件進行加密,如AES。
H(·):{0,1}*->Zp為普通無密鑰Hash函數,如SHA-256。
2.4.1 初始化階段
選擇兩個足夠大的素數p和q來生成RSA模N=pq,并生成QRN的生成元g,將g,N公開。
用戶發送ID給密鑰生成中心,密鑰生成中心選擇兩個隨機數α∈Zp,β∈Zp,計算用戶私鑰(ssk)并將其發送給用戶保存,ssk計算如式4所示:
ssk=α+βH(ID)
(4)
2.4.2 設置階段
在設置階段,用戶將文件數據分塊,并生成各數據塊副本及標簽,將副本發送給CSP存儲,標簽發送至TPA中存儲,CSP確認數據一致無誤后,用戶可刪除本地文件。設置階段的具體流程如下:
(1)ReplicaGen:為了減少驗證開銷并適應多云存儲的分布式環境,用戶將文件F分成n塊,F={b1,b2,…,bn},bi可以看作是一個足夠大的整數。為得到r個副本,用戶使用對稱加密算法對原始數據塊加密bij=Ek(i‖j‖bj),其中i=1,2,…,r,j=1,2,…,n,第i個副本Fi={bi1,bi2,…,bin}。同樣,用戶使用密鑰k可對bij進行解密得到原始數據塊bj。用戶對加密數據塊計算R如式5所示,隨后用戶將r個副本文件{F1,F2,…,Fr}以及R發送給CSP存儲。
(5)
(2)TagGen:對于r×n個副本數據塊,用戶計算每個數據塊的標簽Tagij如式6所示,其中i=1,2,…,r,j=1,2,…,n。Tagi={Tagi1,Tagi2,…,Tagin},用戶將r個副本標簽{Tag1,Tag2,…,Tagr}發送給TPA存儲。
Tagij=gbij*sskmodN
(6)
(3)CSP confirm data:CSP收到用戶發送的數據后,計算以下等式是否成立:
(7)
若相等,則確認數據無誤;否則,它將表明數據存在問題。此時,CSP將拒絕確認數據,并終止存儲服務。此時用戶并未刪除本地文件,所以用戶不會遭受任何損失。如果CSP確認所有數據無誤,服務順利進行,用戶將刪除本地文件。同時,CSO在副本記錄表中記錄副本的存儲地址。
2.4.3 公開審計階段
在公開審計階段,用戶檢查多云存儲服務,以確保外包數據安全存儲在CSP中。為了減少開銷,用戶將批量審計部分副本數據塊,以概率性檢測檢查整個外包數據的完整性。具體審計流程如下:
(1)ChalGen:用戶秘密生成一個足夠大的隨機數s,計算挑戰chal并將其發送給TPA。挑戰chal的計算如式8所示:
chal=gsmodN
(8)
(2)SendChallenge:TPA收到用戶發送過來的chal后,生成隨機序列I和二維數組C:
(9)
I表示e個待審計的數據塊編號序列,C表示對應e個待審計數據塊及r個副本的r×e個系數。TPA將{chal,I,C}發送給CSO,等待CSO返回證據。
(3)ProofCSPGen:CSO分派挑戰,各CSP計算證據返回,CSO聚合證據返回。具體步驟如下:
(a)CSO收到TPA發送過來的審計請求后,查詢副本記錄表找出存儲了待審計副本的CSP,將對應的{I,Ct,chal}分別發送給對應CSP。
(b)CSP收到CSO發送的I={1,3,…,j},Ct={ct1,ct2,…,cte}與chal后,計算其存儲的副本Ft的完整性證明prooft并將其發送給CSO,prooft的計算如式10所示。
(10)
(c)所有CSP返回證據后,CSO聚合證據計算proofCSP如式11所示,其中r為副本個數,CSO將Hash(proofCSP)返回給TPA。
(11)
ProofCSPGen算法流程如下所示:
算法1:ProofCSPGen()
輸入:chal,I,C,{F1,F2,…,Fr}
輸出:Hash(proofCSP)
(1)CSO從副本記錄表中找到存儲了待審計副本的r個CSPid
(2)fortin range(1,r)
(3)CSPt←{I,Ct,chal}
(4)foriin range(1,e)
(5)proofi←chalctibtlimodN
(7)return Hash(proofCSP)
(4)ProofTPAGen:在CSO計算審計證據時,TPA同時依據存儲的標簽以及待審計數據塊編號序列I,和系數數組C計算proofTPA如式12所示,TPA返回證據{Hash(proofCSP),proofTPA}給User。
(12)
(5)Audit:用戶收到TPA返回的證據后,根據用戶秘密保存的隨機數s以及ssk計算等式13是否成立。若成立,則用戶認為CSP完好地存儲了數據;否則,認為TPA或CSP是惡意的,存儲在CSP中的數據可能遭到了損壞。
(13)
3 安全性分析
根據上述安全性假設,假定用戶和CSO是可信的,他們會誠實地執行審計步驟,TPA和CSP是半可信的。在這種背景下,理論上分析所提方法的安全性。
在文中方案,有以下兩種可能惡意破壞公平的云存儲服務的行為:(1)CSP存儲的數據丟失,試圖使用偽造的證明通過驗證;(2)CSP串通TPA偽造證明試圖通過驗證。
定理1(正確性):如果CSP和TPA都誠實地遵守規定的程序,那么證據可以通過User的驗證。
證明:以下等式通過從左到右的推導,證明了Audit算法中的等式是正確的。
(14)
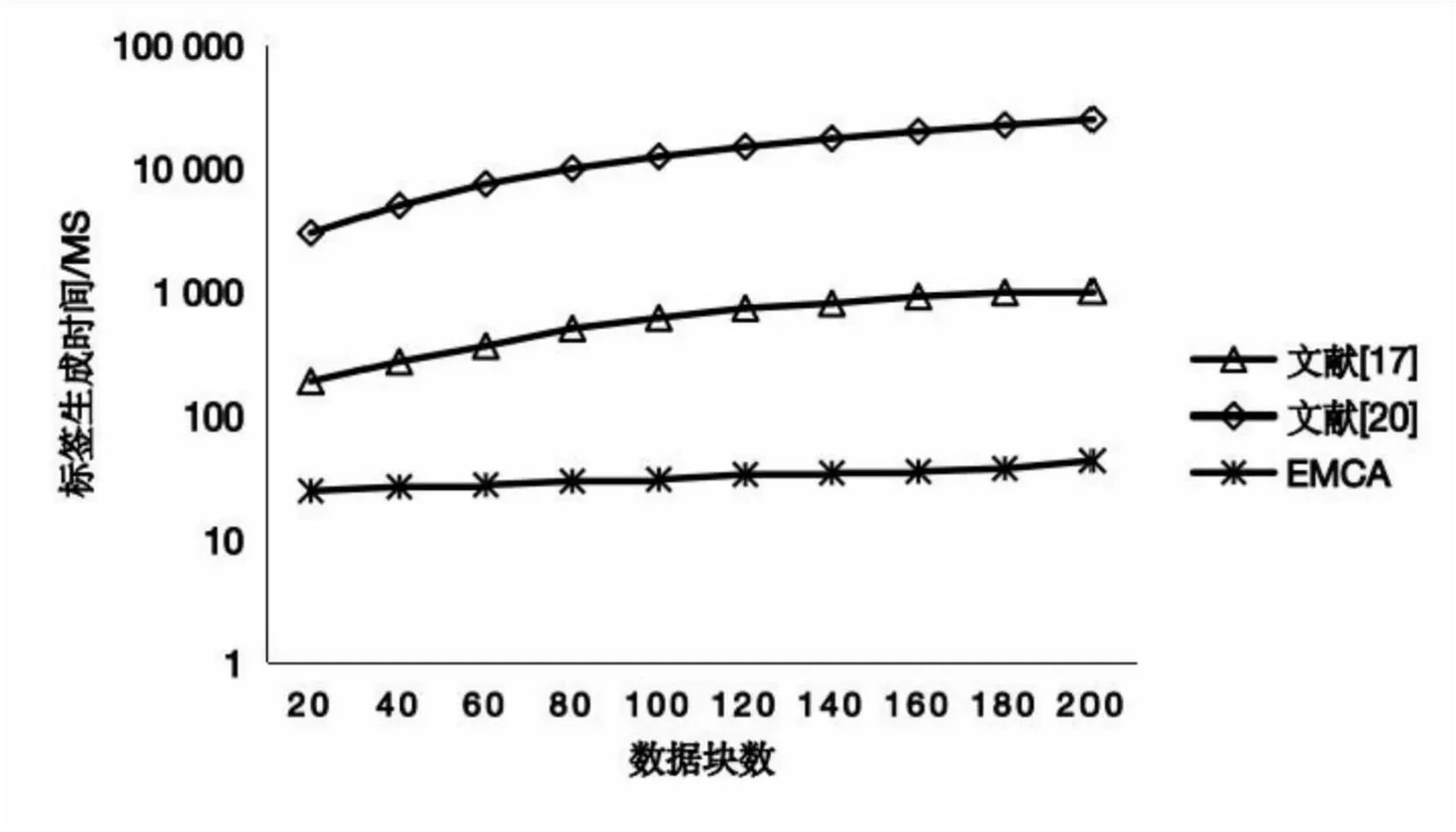
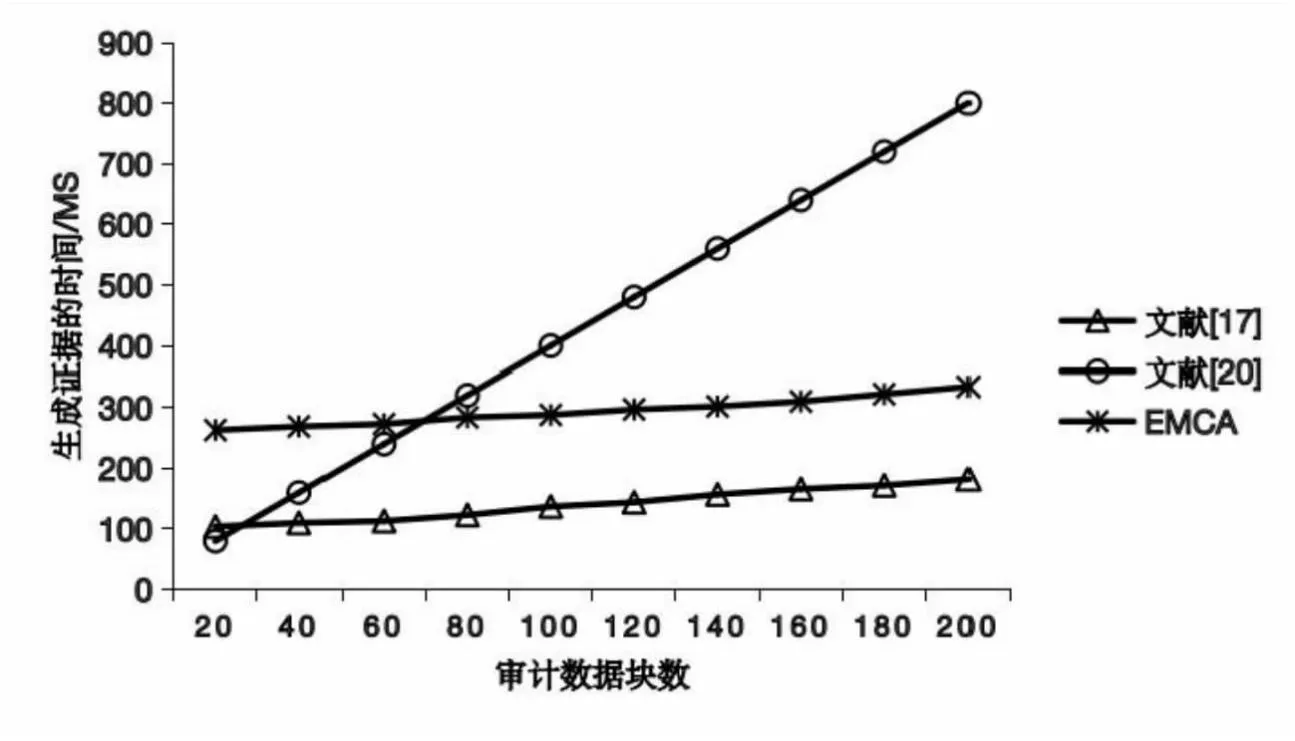
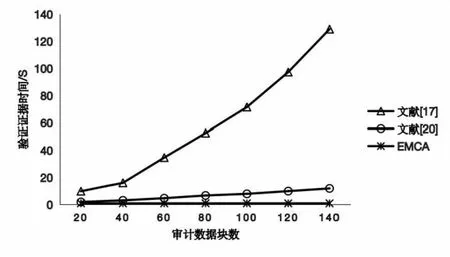
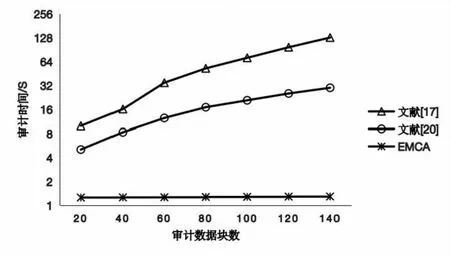
假設1(二次剩余問題):給定一個整數N=p×q,其中p和q是機密的,并且整數g 根據假設1,推導出定理2: 定理2:對于已知g,gsmodN和N的敵手,沒有多項式時間算法可以找到任何滿足s'≠s,N|gs-gs'的s'。 證明:假設存在多項式時間算法A1,對于給定s,g和N=p×q,總能找到一個s'滿足s'≠s,N|gs-gs′,得到以下等式: s≡s'modord(g) (15) 其中,ord(g)是滿足N|gord(g)-1的最小正整數,并且是一個真值與s-s'|ord(g)相同的奇數。若給定g可以滿足ord(g)mod2=1,可以得到以下等式: gord(g)+1≡g(modN) (16) 相應的,也可以得到以下等式: (17) x2≡g(modN) (18) 如上所示,在算法A1的幫助下,可以生成一個多項式時間算法A2來找出滿足x2≡g(modN)的x,而它與假設1相矛盾,由此,定理2的證明已完成。 定理4:CSP串通TPA偽造數據無法通過驗證。 綜上所述,文中方案能夠有效地檢測數據破壞或惡意偽造行為,從而確保數據審計方案能夠安全實施。 該文實現了EMCA和文獻[17,20]的原型系統,實驗證明,EMCA大大減少了審計時間及計算開銷。實驗硬件環境為macOS操作系統,2.6 GHz六核Intel Core i7處理器,16 GB內存。 表3比較了EMCA與文獻[17,20]在標簽生成、證據生成和驗證證據階段的計算開銷。為了簡化表達式,使用Tmul,Texp,Tp,Thash和Tadd分別代表一次乘法運算、一次冪運算、一次雙線性對運算、一次Hash運算和一次加法運算所需的時間。其中,n為數據塊總數,r為副本數,e為批量審計的數據塊數。對比得出,在標簽生成和驗證證據階段,EMCA都是具有優勢的,在整個審計過程中,與文獻[17,20]相比,文中方案具有更低的計算開銷。 表3 EMCA與文獻[17,20]的計算成本比較 該文選擇了0~200個數據塊,5個副本,10個云存儲服務器來比較EMCA與文獻[17,20]在標簽生成、證據生成和驗證證據時的計算開銷。 圖2顯示了標簽生成的比較結果。當數據塊數為200時,EMCA需要44 ms,而文獻[17]需要1 010 ms,文獻[20]需要2.5 s。很顯然,文中方案的時間消耗要遠小于文獻[17,20]的時間消耗。 圖2 標簽生成的計算成本比較 圖3顯示了證據生成的比較結果。當審計數據塊不斷增多時,EMCA的計算成本比文獻[17]的高,原因在于EMCA的計算成本集中在證據生成階段,審計階段所用開銷極小;而文獻[17]的計算開銷集中在審計階段,證據生成階段開銷較小。 圖3 證據生成的計算成本比較 圖4顯示了驗證證據階段的比較結果。EMCA開銷最小,當數據塊數為100時,EMCA只需不到1 s,而文獻[17]需要71 s,文獻[20]需要8 s。很顯然,在審計階段,文中方案的計算成本遠低于文獻[17,20]的計算成本。原因在于EMCA驗證階段只需進行兩次模冪和兩次哈希,計算成本與審計數據塊數無關,而文獻[17,20]需要三次雙線性對配對和多次哈希、冪運算、加法和乘法,且計算成本隨審計數據塊數增加而增加。 圖4 驗證證據的計算成本比較 圖5顯示了一次完整的審計過程的計算成本比較。從一次完整的審計過程來看,EMCA的計算開銷遠小于文獻[17,20]的計算開銷,如當審計數據塊為100時,文獻[17]一次審計需要71.8 s,文獻[20]需要21 s,而EMCA只需1.3 s。原因在于EMCA舍棄了計算昂貴的雙線性映射運算,采用了模冪加密技術來保證效率與安全。 圖5 一次審計的計算成本比較 針對現有的多副本數據審計方案的不足,該文提出了一種在多云情景下的多副本數據完整性驗證方案,副本數據可存儲在不同的云存儲服務器中,采用第三方審計者協助審計,通過同態可驗證標簽可一次批量審計所有抽樣副本,大大提高了審計效率。實驗分析與評估表明,該方案是安全和高效的。未來的工作是改進方案使用戶不必參與審計過程,以減輕用戶端負擔。
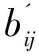
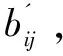
4 性能分析
4.1 理論分析

4.2 實驗分析
5 結束語

