基于ARCTAN 函數的孤島微電網下垂控制研究

朱航航, 李夢達, 寧 晗, 裴光耀, 孫悅悅

(上海電機學院 電氣學院, 上海 201306)

為實現“碳達峰、碳中和”的目標,同時滿足現代化社會發展對能源的需求,需要建立一個以新能源發電為主體的新型電力系統,微電網作為充分利用分布式新能源發電的一種高級應用形態而受到廣泛關注。在微電網中,新能源產生的電能大多為直流源,而逆變器作為將直流電轉化為交流電的關鍵器件,對微電網運行至關重要。

目前,針對微電網逆變器的控制方式主要有集中控制[1-3]、主從控制[4-6]、下垂控制[7-9]等。下垂控制因具有控制簡單、靈活、低成本、可靠性高等特點而廣泛應用于逆變器控制中。下垂控制利用頻率和電壓偏移控制逆變器的輸出功率,以滿足系統運行需求。但由于逆變器下垂控制采用比例控制,在頻率和電壓誤差之間具有不可調和性。

針對上述問題,已有大量的改進型的下垂控制方案被提出,方法各異。王岳等[10]通過采用PID控制器設計頻率補償器,達到微電網在孤島運行有功功率發生變化時保持系統頻率穩定的目標。吳麗珍等[11]設計了一種控制方案,利用模型預測控制方法穩定微電網的頻率,從而提高微電網穩定性。柴秀慧等[12]對下垂控制進行改進,提出并網和離網進行統一控制的策略。余志文等[13]利用分布式通信,提出了一種自適應下垂控制策略解決頻率偏差。陳剛等[14]利用分布式優化調度解決方案,提出了一種新型的下垂控制器,以確保微電網頻率能夠穩定維持在額定值。黃慧等[15]在考慮新能源互補特性的基礎上提出復合儲能協調控制策略,確保母線電壓調節至允許范圍。劉堯等[16]提出了一種同步發電機的自適應控制策略,以增強系統頻率的動態穩定性。孫亮等[17]對虛擬同步發電機無差調頻控制策略進行改進,可實現頻率自動調節和輸出功率合理分配目標。黎靜華等[18]提出一種協同控制的微電網頻率穩定性控制策略,達到了抑制系統頻率波動的目標。姚建華等[19]提出一種基于強化學習的控制方法,利用多個新能源調節微電網運行在孤島情況時的頻率。于國星等[20]提出一種兩層控制結構,實現頻率同步控制、頻率無差調節的目標。

上述文獻對傳統下垂控制進行了改進以消除頻率偏差,但這些改進方案存在輸出功率不均衡及優化目標復雜等問題。為解決以上問題,改進的下垂控制應滿足頻率穩定的要求,且達到輸出功率均衡、無需通信、結構簡化的目的。為此,本文引入ARCTAN函數改進傳統下垂控制,當微電網發生擾動時,能夠抑制頻率波動,使頻率達到系統要求,以增強微電網運行的穩定性。

1 多臺逆變器并聯模型分析

為準確分析逆變器并聯運行模式,本文以兩臺逆變器系統并聯運行為例進行分析,如圖1所示。圖中,R1、R2為逆變器到公共點之間的線路電阻;L1、L2為逆變器濾波電感;C1、C2為逆變器濾波電容;Z為兩臺逆變器的公共負載。設公共負載Z的電壓為Uo,逆變器輸出電壓與負載電壓間相角差為δi,則逆變器1輸出的電壓為E1∠δ1,逆變器2輸出的電壓為E2∠δ2,兩臺逆變器的輸出電流分別設為Io1和Io2,逆變器輸出的有功功率分別表示為P1和P2,輸出的無功功率分別表示為Q1和Q2。

圖1 逆變器并聯模型

由圖1逆變器并聯模型電路可得逆變器輸出有功和無功功率的表達式為

式中:Xi(i=1,2)為線路電抗和逆變器輸出電抗。

2 傳統下垂控制分析

傳統高壓大電網線路呈現感性,分析系統運行時可忽略電阻,同時因相角較小,即sinδ≈δ≈0,因此式(1)可簡化為

由式(2)可知,相角δi影響逆變器輸出的有功功率,逆變器輸出無功功率受到電壓幅值Ei影響。由于相角的變化不明顯,實際多用角頻率ω來表示相角的變化。因此,得到傳統下垂控制方程為

式中:ωi、Ei分別為逆變器實際輸出的角頻率和電壓幅值;ω*、E*分別為額定角頻率和電壓幅值;P*、Q*分別為額定的有功功率和無功功率;mi為逆變器有功功率下垂控制系數;ni為逆變器無功功率下垂控制系數。

在逆變器實際運行過程中,系統出現輕微的波動,即逆變器出力或者負荷需求小幅度波動時,功率與角頻率偏移較小,傳統的下垂控制能夠維持系統的穩定運行。當系統出現較大的波動,即逆變器出力或者負荷需求大幅度變化時,如圖2中傳統下垂控制曲線所示。此時角頻率將由ω1偏移到ω2,偏移量過大將會影響系統的安全穩定運行。

圖2 傳統下垂控制ω-P 關系曲線

3 改進下垂控制方法

3.1 新型下垂控制方程

在孤島模式下,當大容量負荷投入或電源停機時,微電網系統在傳統下垂控制模塊的作用下,系統頻率可能會超出限制,并且此狀態將持續一段時間,導致微電網系統的電能質量降低,影響系統穩定運行。為減少頻率波動,提高系統運行的穩定性,本文將ARCTAN函數引入下垂控制中。圖3為ARCTAN形式下垂控制流程。

圖3 ARCTAN形式下垂控制流程

首先,將采集的電壓、電流進行坐標變換,計算出有功功率P,再進行ARCTAN 變換,得到新的系統頻率,改進后的下垂控制方程可表示為

式中:G取值為1,也可以根據系統控制效果進行改變,得到理想的系統響應速度和系統運行穩定性。

ARCTAN形式下垂控制函數關系曲線如圖4所示。

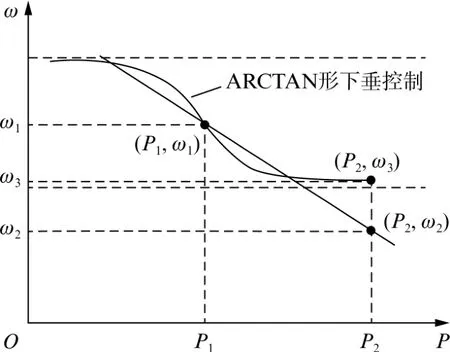
圖4 ARCTAN形式下垂控制函數關系曲線

在傳統下垂控制中,當系統輸出有功功率變化或者負載出現較大的波動時,頻率偏移較多,頻率會由ω1偏移到ω2,超出頻率下降的允許范圍。改進型下垂控制頻率由ω1偏移到ω3足夠大時,ω將趨近于ω*,相較于傳統下垂控制頻率下降量更小。從理論層面分析基于ARCTAN 函數改進下垂控制保證系統頻率穩定的原因,將式(4)等號右側在系統穩定參考運行點(ωref,Pref)進行Taylor展開,展開式為

由式(5)可見,基于ARCTAN 形式下垂控制函數的Taylor展開首項是傳統下垂控制函數項。當系統波動導致有功功率波動較小時,Taylor展開式的高次項接近零,控制效果與傳統下垂控制效果相似。當系統有功功率波動較大時,函數的高次項發揮作用,穩定系統頻率。

ARCTAN形式的下垂控制能夠大幅增強頻率的穩定性,與傳統下垂控制形成鮮明對比。其能夠將頻率控制在允許波動范圍內,以增強微電網運行的穩定性。

3.2 系統穩定性分析

為研究本文控制策略的穩定性,對系統靜態工作點附近進行線性化處理,建立逆變器小信號模型進行穩定性分析。逆變器輸出的有功功率及無功功率可由式(1)表示,假設系統穩態的工作點為(δ0,E0,U0),可得到相關的小信號方程為

式中:

在下垂控制中,低通濾波器會將計算測量的功率中的高頻部分濾除,則有

式中:ωc為低通濾波器的截止頻率;Δω(s)=sΔδ(s),s為拉普拉斯算子。

簡化式(7)可得系統的特征方程為

其中:

利用根軌跡對系統特征方程的解進行系統分析。圖5為當其他控制參數固定時,系統下垂系數變化對應根軌跡分布情況,設定圖中箭頭方向為系統參數增大的方向。

圖5 參數m 變化時系統的根軌跡

隨著下垂系數的增加,系統的特征根軌跡表現為往虛軸偏移趨勢,對系統的穩定性產生影響。當采用改進下垂控制時,抑制了有功功率變化,可增強系統的穩定性。

4 控制策略仿真

為驗證本文提出的ARCTAN 形式下垂控制的有效性,在Matlab/Simulink平臺上建立兩臺逆變器的并聯仿真模型,兩臺逆變器容量設定相同,采用理想的直流電源為逆變器供能,仿真參數如表1所示。為盡可能貼近實際,考慮線路壓降,交流側輸出的電壓幅值設定為比額定值高5%,即327.55V。為便于觀察,由式ω=2πf,將角頻率轉化為頻率。

表1 仿真參數

4.1 傳統下垂控制仿真分析

兩臺逆變器同時連接到負載,為負載供電。逆變器控制方式為傳統下垂控制,系統仿真時間設置為1s。設定系統頻率參考值為50Hz,當t∈[0,0.5)s時,系統投入負載開始運行;當t∈[0.5,1)s時,增大系統負載。仿真結果如圖6和圖7所示。

圖7 頻率變化曲線

由圖6可知,在開始仿真后,系統直接帶載運行,很快進入穩定狀態,穩定時兩臺逆變器輸出有功功率約為5.3kW,實現了功率均勻分配。0.5s時使輸出有功功率增加,系統很快進入穩定狀態,兩臺逆變器輸出的有功功率約為21kW,達到功率平衡。由圖7可知,在0～0.5s內,系統頻率由50Hz下降到49.78Hz,0.5s時輸出有功功率增加,頻率由49.78Hz下降到49.64Hz,超出規定頻率偏差±0.2Hz的范圍。

4.2 改進下垂控制仿真分析

兩臺逆變器同時連接到負載,為負載供電。此時控制方式為ARCTAN形式下垂控制,仿真時間同樣設置為1s。設定系統頻率為50Hz,在t=0.5s增大系統負載,仿真結果如圖8和圖9所示。

圖8 逆變器輸出有功功率曲線

圖9 系統頻率變化

由圖8可知,兩臺逆變器在0～0.5s之內,輸出有功功率逐漸由0增大至約5.3kW,保持穩定;在0.5s增加有功功率的輸出后,輸出有功功率達到約21kW 后保持穩定。觀察頻率變化,由圖9(a)和圖9(b)可知,在整個系統運行時間段內,系統頻率保持穩定,為49.99Hz附近。結果表明,本文ARCTAN形式下垂控制方法能夠有效抑制系統頻率波動,增強系統運行的穩定性。

5 結 語

微電網的系統頻率和國家電網運行的頻率偏差過大將會影響電網安全以及電能質量。在傳統逆變器下垂控制中,存在著輸出頻率隨輸出有功功率增加而產生偏移的問題。針對該問題,分析了傳統下垂控制存在的問題,提出了ARCTAN 形式下垂控制的概念,并進一步用仿真模型驗證。結果表明,運用ARCTAN 形式下垂控制策略,微電網的頻率能夠保持在國家電網規范的頻率內,該控制策略能夠改善頻率偏移的問題,增強系統穩定性。