基于滑模控制的軌道式無線電能傳輸系統設計

趙榮強, 胥 飛

(上海電機學院 電氣學院, 上海 201306)

無線電能傳輸(Wireless Power Transmission, WPT)具有安全、便捷、用戶體驗好等優點,得到廣泛關注[1-3]。由于WPT可以實現無接觸式電能傳輸[4],被廣泛應用于固定式充電和動態式充電,如電動汽車[5-6]、物流傳送等方面。由于WPT 系統的發射線圈與接收線圈之間并不完全耦合,從而導致WPT效率不高,因此需要加入補償模塊,以提高電能的傳輸效率[7-8]。為優化輸出特性,文獻[9-12]分別提出了LCL、LLC、CLC以及LCC等高階諧振補償拓撲。傳統軌道式WPT 系統大多采用串聯串聯的低階補償拓撲,文獻[13]的接發線圈采用E型鐵氧體結構,需要鐵氧體物料成本更高,較大的等效內阻造成效率低于75%。

本文提出一種基于新型接發線圈結構的LCC-S型補償拓撲的WPT系統,采用利茲線纏繞C型鐵氧體作為接收線圈,并套在軌道式雙匝線圈組成的發射線圈上。相比傳統串聯串聯型補償拓撲的軌道式WPT結構,該結構等效電阻較小,傳輸效率較高,電壓增益可調,且輸出特性更好,可用于物流傳送、流水線供電等方面。本文為便于接收端電壓控制,選擇接收端為恒壓輸出特性的LCC-S型高階補償結構進行設計,并加入基于滑模控制的穩壓控制器進行雙端控制,以達到接發線圈相對位置變化時電壓保持不變的目的。最后,通過搭建實驗平臺驗證所設計的新接發線圈結構和滑模控制器的可行性。

1 基于LCC-S的WPT系統建模

基于LCC-S的WPT 等效電路如圖1所示。圖中,R0為發射端的補償內阻;Rp、Rs分別為發射線圈、接收線圈的內阻;Lp、Ls分別為發射線圈、接收線圈的自感;M為接發線圈之間的互感;Cfp、Cp分別為發射端并聯、串聯補償電容;L0為發射端補償電感;Cs為接收端補償電容;Us為直流電源逆變后的交流電;I0、I1、I2分別為補償線圈、發射線圈、接收線圈的電流;Rload為負載電阻。

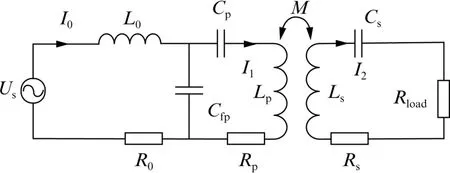
圖1 基于LCC-S的WPT系統等效電路

由圖1可知,接收端阻抗為

式中:ω為系統諧振角頻率。

接收端側反射至發射側的等效阻抗為

式中:M=K LpLs,K為線圈耦合系數。

系統總輸入阻抗為

為實現系統諧振,發射端并聯電容Cfp需與發射端補償電感L0諧振,串聯補償電容Cp、并聯補償電容Cfp和發射線圈電感Lp也要形成諧振,使得發射線圈電流近似等于逆變電路輸出電流,此時各參數因滿足:

由式(4)和式(5)可知,Lp＞L0,令L0=aLp,a為常數且0＜a＜1。由式(4)～式(6)可計算出補償電容值為

代入電容值后,發射端補償拓撲諧振頻率、接收端補償拓撲諧振頻率和耦合線圈的諧振頻率與系統諧振頻率相同,系統完成磁耦合諧振,此時系統反射阻抗和輸入阻抗可簡化為

忽略線圈寄生電阻,各支路電流為

此時系統傳輸效率為

忽略線圈寄生電阻,簡化式(12)～式(14)并計算出負載兩端電壓和輸出電流為

從式(16)、式(17)可以看出,在忽略內阻的情況下輸出電壓與發射端補償電感L0、互感M、輸入電壓Us有關,與負載電阻值無關,因此可以大致實現變負載恒壓,但是互感變化時不能恒壓,需加入控制電路保證系統穩定供電。

2 接收端對系統效率的影響

電磁耦合線圈是WPT系統的關鍵部件,本文將從磁芯結構、導線特性、負載特性等三方面論述接收端對系統效率的影響[14]。

2.1 接收端磁芯結構的影響

軌道式WPT系統與松耦合變壓器相比,具有接發線圈氣隙大、軌道線圈長等特點,因此軌道線圈與接收線圈之間的漏感大、耦合系數低,從而使發射端的能量向接收端轉移十分困難。因此,合理設計鐵氧體磁芯結構,可減少漏磁通,提高系統效率。通過式(15)可知,影響效率的因素主要有接收線圈內阻、耦合系數及負載電阻大小,因此,在設計磁芯結構時,應使得在互感合適的情況下,線圈內阻盡量小。傳統軌道式WPT 系統采用E型鐵氧體磁芯如圖2(a)所示,本文提出一種C型鐵氧體磁芯結構,如圖2(b)所示。

通過在Maxwell電磁仿真軟件中搭建接發線圈模型可以求解出線圈自感、等效電阻和它們之間的互感[13]。該軟件可以利用靜磁場、渦流場或瞬態場等對兩側諧振線圈完成三維的有限元仿真。利用Maxwell電磁仿真軟件對傳統E型磁芯結構和本文提出的C 型鐵氧體結構進行電磁耦合仿真。

發射端線圈設為3000股線徑0.1mm 利茲線繞雙匝形成8m 供電軌道。根據E型和C型鐵氧體尺寸數據設置相關參數,建立發射端和接收端線圈耦合模型,分別將E型和C型鐵氧體磁芯組成的接收端線圈套在發射線圈軌道上,設置接收線圈導線直徑為8mm,導線截面積為1mm2,諧振頻率為85kHz,在E型和C型鐵氧體磁芯上分別繞15及31 匝,使得互感相同,發射端通入高頻交流電。

在參數選項卡中選擇矩陣,添加兩線圈,并勾選測量接發線圈之間的互感、自感和耦合系數,便可在結果選項卡中得出相關參數,導出C型與E型接收裝置參數并對比,如表1所示。

由表1可知,大致相同的互感下,接收端為E型鐵氧體磁芯的接收線圈與發射線圈的互感較高,但是等效電阻較大,以下分析這兩個參數對系統效率的影響。

2.2 接收線圈導線特性的影響

為研究耦合系數和接收線圈等效電阻對系統效率的影響,設定系統工作頻率為85kHz,確定互感系數之后計算得出其他補償元器件的參數,將表1中的線圈自感、耦合系數等參數代入式(10)、式(12)、式(16)中,繪制耦合系數分別為0.27 和0.18時,系統效率隨接收線圈等效電阻變化的曲線,如圖3所示。

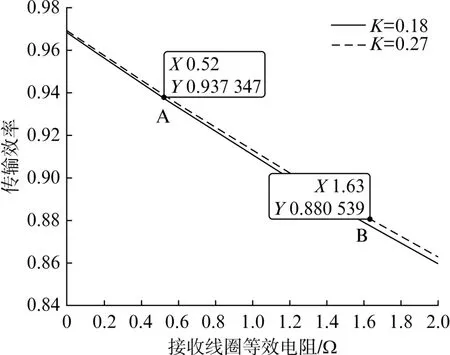
圖3 不同耦合系數下等效電阻和效率關系

由圖3可知,在相同電阻下,耦合系數高的E型鐵氧體傳輸效率較高,但是系統傳輸效率隨著接收線圈等效電阻的增大而減小更為明顯。通過A、B兩點可知,C型鐵氧體結構的接收線圈效率比E型鐵氧體結構的接收線圈高將近6%,并且C型鐵氧體磁芯更適合在軌道上移動,因此本文選擇C型鐵氧體磁芯,可提高系統效率。

2.3 負載阻值對傳輸效率影響

為尋求負載阻值對傳輸效率的影響,將表1中C型鐵氧體參數代入式(10)～式(12)、式(16)中,利用Matlab繪圖軟件,系統最佳效率點的阻值為16Ω,由此可得C型鐵氧體構成的WPT系統各項參數如表2所示。

表2 C型鐵氧體系統參數

3 LCC-S型WPT系統仿真設計

為實現LCC-S 型WPT 系統能穩定高效供電,本文利用Matlab/Simulink仿真軟件搭建了仿真模型,為模擬負載在軌道上運動時耦合系數發生變化,利用松耦合變壓器模型可設置發射線圈和接收線圈的自感和等效電阻及兩者之間的互感。采用階躍信號發生器模塊控制開關控制3個耦合系數分別為0.18、0.13、0.21的松耦合變壓器模型,分別在0s、0.03s、0.06s時刻接入電路。不加控制開始仿真,發現輸出電壓會隨耦合系數的變化而變化。為保證系統能穩定供電,本文采用雙端控制,在接收端增設BUCK電路,通過控制發射端逆變器占空比及BUCK 電路占空比達到穩壓目的。傳統PI控制調節參數較多,響應速度慢,對擾動比較敏感。本文提出一種無抖振滑模控制方法以消除滑模抖振,使得滑模面趨近速度快,相比PI控制,無抖振滑模控制只需輸入較少的信號即可控制輸入電流和輸出電壓,暫態性能和魯棒性均可達到應用要求[15]。

在Matlab/Simulink仿真軟件中搭建了雙端無抖振滑模控制仿真模型,現有一系統狀態方程˙x=f(x,u,t),x,u,t∈R。滑模面設計如下:

式中:α、β為滑模系數,需滿足Hurwitz條件即都大于0。

令s=0,將系統電路方程代入滑模面,可得

高新區搞活存量盤活 促進高效利用見真章（薛文奇） ....................................................................................3-55

將滑模面對時間求導,可得

式中:ζ為阻尼系數,ζ=0.5α;ωn為無阻尼自然振蕩頻率,ωn=。

本文采用基于等速趨近律的積分滑模控制,設計要求快速逼近滑模面,所以本文針對過阻尼狀態設計滑模系數,選取ζ=1.3,衰減系數代表系統調節時間,決定控制器的控制速度。滑模系數α=,β=,系統響應速度τ取值越大,系統響應越慢;τ取值越小,系統響應越快。考慮到滑模控制律中包含的濾波電容Cf取值較小,所以選取α=4.6×106,β=3.13×1012。為保證＜0,滑模控制律如下:

利用Matlab/Simulink搭建對應模型,進行仿真,在0.03s和0.06s時刻改變互感值,并與基于PI控制所得到的輸出電壓波形進行對比,如圖4所示。

圖4 閉環‐互感改變‐輸出電壓波形

從電壓波形來看,在0.03s和0.06s時刻耦合系數發生變化時,PI控制要經過2.36ms后才能穩定到預設值15V,且超調量及紋波較大,而滑模控制系統僅需1.47ms即可穩定到預設值,紋波及超調量更小,能夠很好應對接收端在軌道上運動時耦合系數不穩定的情況。

4 系統設計與實驗驗證

為驗證上述理論的正確性,搭建實驗平臺。設定系統工作頻率為85kHz,逆變電路PWM 波的頻率為85kHz,保證整個系統在同一諧振頻率下。發射端接收端采用STM32F103C8T6完成PWM 信號產生及電壓電流信號的采集,通過編程實現移相控制,將直流電逆變為85kHz的高頻交流電,輸入LCC補償模塊,接收端同樣通過STM32F103C8T6的ADC1的PA4引腳設置為獨立模式完成信號采集后送入芯片,通過藍牙模塊與發射端逆變板進行通信,加入滑模算法控制占空比輸出,完成對電壓的控制。

為研究接發線圈相對位置變化對輸出電壓的影響,可將發射端線圈慢慢抬升,控制其他參數不變,使接發線圈距離由開始時距離為0cm 分8次增加至4cm。通過示波器觀察不加控制、加入PI控制、加入滑模控制的輸出電壓,得到實驗數據繪制出電壓隨接發線圈相對距離變化如圖5所示。

通過輸入功率除以輸出功率可以得到系統效率,3種控制方法傳輸效率如圖6所示。

由圖5、圖6可知,滑模控制算法穩壓效果明顯優于其他兩種控制方法,根據負載要求,輸出電壓與預設值15V 偏差不能高于0.5V,所以只有滑模控制算法能滿足系統接發線圈距離為0～3cm 時穩壓輸出,在效率方面不加控制時系統效率最高,而滑模控制的效率要比PI控制的效率高5%左右。

5 結 論

本文首先借助Maxwell仿真對比C型鐵氧體和E型鐵氧體磁芯繞制的發射線圈的相關參數,并使用Matlab進行分析,證明C型鐵氧體的傳輸效率較高。然后,通過數學建模確定了LCC-S拓撲結構的諧振條件,根據已知參數設計其他元件參數,并在Matlab/Simulink里分別搭建基于PI控制和滑模控制的仿真模型進行對比,證明滑模控制效果要優于PI控制。最后,搭建實驗樣機進行實驗,實驗證明當接發線圈相對位置在0～3cm 變化時,滑模控制算法能滿足電壓偏差小于0.5V的要求,并且傳輸效率要高于PI控制算法。