Lamb波模態體聲波壓電諧振器仿真研究

崔向東,趙 穎

(中國人民解放軍軍事科學院 系統工程研究院,北京 100142)

0 引言

現代通信技術的快速發展使得傳統的大體積石英晶振等逐漸被淘汰,取而代之的是性能更好、體積更小的微機電系統(MEMS)器件。同時射頻器件對高性能時鐘電路提出了更高的要求,信號處理器件需要具有低插入損耗、高帶寬、低溫漂等特性,而聲學MEMS諧振器恰好滿足此需求。目前主流的聲學諧振器包括聲表面波(SAW)諧振器和體聲波(BAW)諧振器。其中SAW諧振器由于激勵的頻率較低,只能應用于低頻段器件,而BAW諧振器工作頻率在兆赫茲～吉赫茲頻段,且其具有體積小,品質因數(Q)高,功率承載能力強,以及與集成電路工藝易兼容等優點[1]。但是傳統的BAW諧振器的諧振頻率主要由壓電層厚度決定,而厚度方向激勵的體聲波難以同時滿足高頻和大帶寬的需求[2];結合了各種壓電材料的特性并在諧振體激勵蘭姆(Lamb)波模態,則能使諧振器兼容SAW器件的多頻段和薄膜體聲波諧振器(FBAR)器件的高頻特性,從而實現具有較高頻率和Q值、多頻段可集成的壓電BAW諧振器[3-5]。近年來科研人員對提高Lamb波模態諧振器的性能參數展開了諸多研究,主要圍繞提升諧振器的Q值、諧振頻率、機電耦合系數等參數進行探討。其中Q值反映了諧振器的能量耗散水平,體現在濾波器的插入損耗和振蕩器的相位噪聲等方面;機電耦合系數反映了機械能與電能之間的轉換效率,諧振頻率和機電耦合系數體現在濾波器工作帶寬等方面。對于Q值的提升,主要從能量損耗機制方面進行研究,如錨固損耗、空氣阻尼、熱彈性阻尼等[6]。錨固損耗為諧振器振動時,聲波通過諧振腔與襯底之間的連接部位損耗能量,該損耗可通過優化錨的結構或選擇剛度較大的材料制作錨,以減小錨損阻尼。

本文圍繞錨系繩的設計和壓電材料的選擇進行研究,建立了基于叉指換能器的壓電BAW諧振器模型,并利用有限元分析軟件對4種錨結構產生的錨損以及3種壓電材料給器件帶來的性能進行討論,器件激勵在Lamb波S0模態工作。此外,本文對由BAW諧振器構成的BAW濾波器進行仿真實驗,分析其所能實現的頻帶范圍。

1 Lamb波諧振器工作原理

Lamb波是一種體聲波,由縱(L)波和垂直剪切(SV)波結合形成,故而在振動方向上具有兩個分量,一個是與聲波傳播方向平行的L分量,另一個是與聲波傳播方向垂直且與厚度方向一致的SV分量。常見的蘭姆波諧振器通過對頂部叉指電極和底部板電極施加電信號,激勵中間壓電層產生壓電效應發生形變,在諧振腔內反射形成駐波引起諧振,從而激勵聲波[7-8],其基波共振頻率為

(1)

式中:v為壓電層體聲波相速度;λ為體聲波波長;P為叉指電極周期。蘭姆波的振動頻率主要受壓電層厚度的影響,所以具有頻散特性,可分為對稱(S)蘭姆波和非對稱(A)蘭姆波,其中S型蘭姆波的特征方程[9-10]定義為

(2)

A型蘭姆波的特征方程定義為

(3)

其中:

(4)

(5)

式中:ci和ct分別為縱波和橫波波速;ω,k分別為固有角頻率和波數;H為壓電層厚度。

通過對諧振器的等效電路模型進行理論分析可以提取出器件的關鍵性能參數。基于壓電效應的諧振器等效MBVD模型如圖1所示。

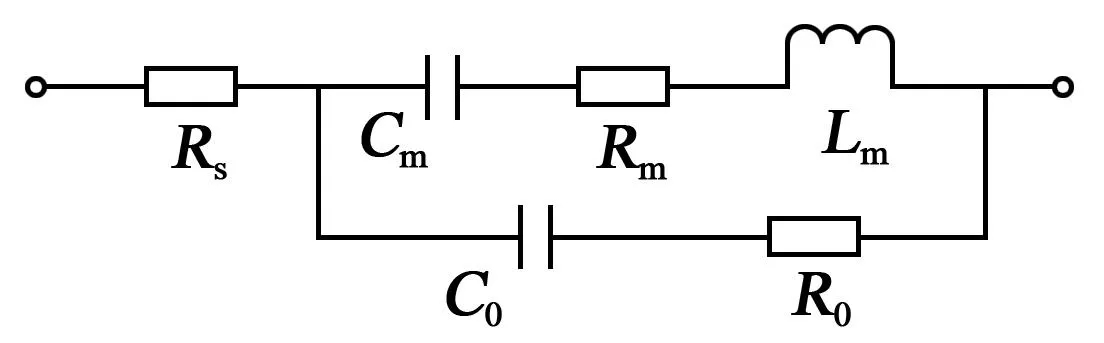
圖1 壓電諧振器等效MBVD模型

圖1中,Rs為因金屬互連引起的損耗,Rm為諧振器在諧振時的損耗。由Cm、Rm、Lm組成的分支稱為運動臂,由C0、R0組成的分支稱為靜態臂。根據該等效電路模型,諧振器的諧振頻率fr和反諧振頻率fa分別為

(6)

(7)

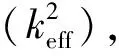
(8)

(9)

2 諧振器結構設計和模型建立

本文所設計的蘭姆波壓電諧振器采用電極-壓電層-電極的三明治結構,如圖2(a)所示,其中頂電極設計為叉指(IDT)電極,底電極為板電極,電極材料選用鉬(Mo),該材料是MEMS中常見的具有高聲阻抗和低電阻率的金屬材料,作為電極能夠有效提高器件Q值[12]。為了激勵S型Lamb波模態(見圖2(b)),在叉指電極上交替施加極性相反的電壓,底部板電極作為接地端,使頂電極與底電極之間的壓電層內部形成極性相反的電場,從而產生方向相反的形變。器件壓電層厚度H=1 μm,叉指電極間距P=62.5 mm,電極厚度Hm=200 nm,電極寬度W=25 μm,諧振器全長L=1 425 μm,有效孔徑Le=1 260 μm,電極個數n=6。為了有效計算產生錨固損耗后諧振器的Q值,本文建立了基于完美匹配層(PML)的有限元模型,將邊緣襯底設定為PML,以吸收通過支撐梁耗散出去的能量。此外,由于電極層和壓電層厚度相對于器件的長度和寬度,尺寸差異非常大,相當于一個薄板結構。在網格劃分過程中,壓電層選用自由四面體網格,并控制自由四面體網格在x、y、z方向上以3∶2∶20的比例進行縮放,在邊緣襯底部分采用映射網格并進行掃掠,建立的網格剖分如圖3所示。

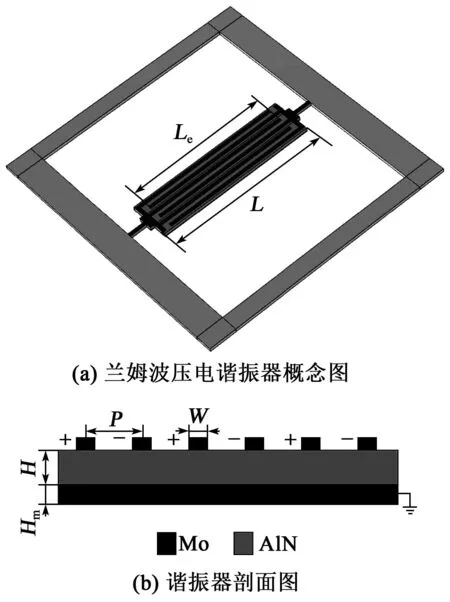
圖2 諧振器幾何圖

圖3 諧振器模型網格剖分

3 器件不同錨結構設計與仿真

本文利用有限元分析軟件建立了4種不同錨系繩結構的BAW諧振器模型,并分析錨結構對器件Q值的影響。諧振腔通過支撐錨與邊緣二氧化硅(SiO2)襯底部分連接,諧振腔底部為鏤空部分,實現了腔體底部與空氣的阻抗不匹配,有效形成聲波反射。邊緣襯底邊界條件設置為PML域,使其有效吸收聲波并計算Q值。在有限元分析軟件的特征頻率研究中引入Q值的計算方式,有:

(10)

式中ω為求解的器件固有角頻率。在器件存在阻尼的情況下,角頻率具有虛部Im(ω)和實部Re(ω),虛部與實部之比反映了阻尼的大小。

所構建的4種錨結構分別為直梁型、梯形梁、框架-梁型及末端帶槽型支撐錨。對于支撐錨的設計,當支撐錨的共振頻率與諧振體的共振頻率相匹配時,造成的錨損失最嚴重,而對于給定的錨結構寬度W,若要達到頻率匹配,則支撐錨的長度L需滿足[13]:

(11)

(12)

式中:E為諧振腔楊氏模量;ρ為密度;f0為共振頻率;λi為特征模態相關系數。為了避免支撐錨與諧振腔發生頻率匹配,錨的長度設計需要遠離L,通常將支撐錨設定為λ/4的奇數倍(其中λ為波長),以達到最大的阻抗失配。本文將錨長度設定為5λ/4,且為了控制錨與諧振腔的接觸面面積對器件性能的影響,所構建的4種錨與諧振腔的接觸面寬度相同。圖4是4種錨結構下的諧振器有限元位移仿真圖。

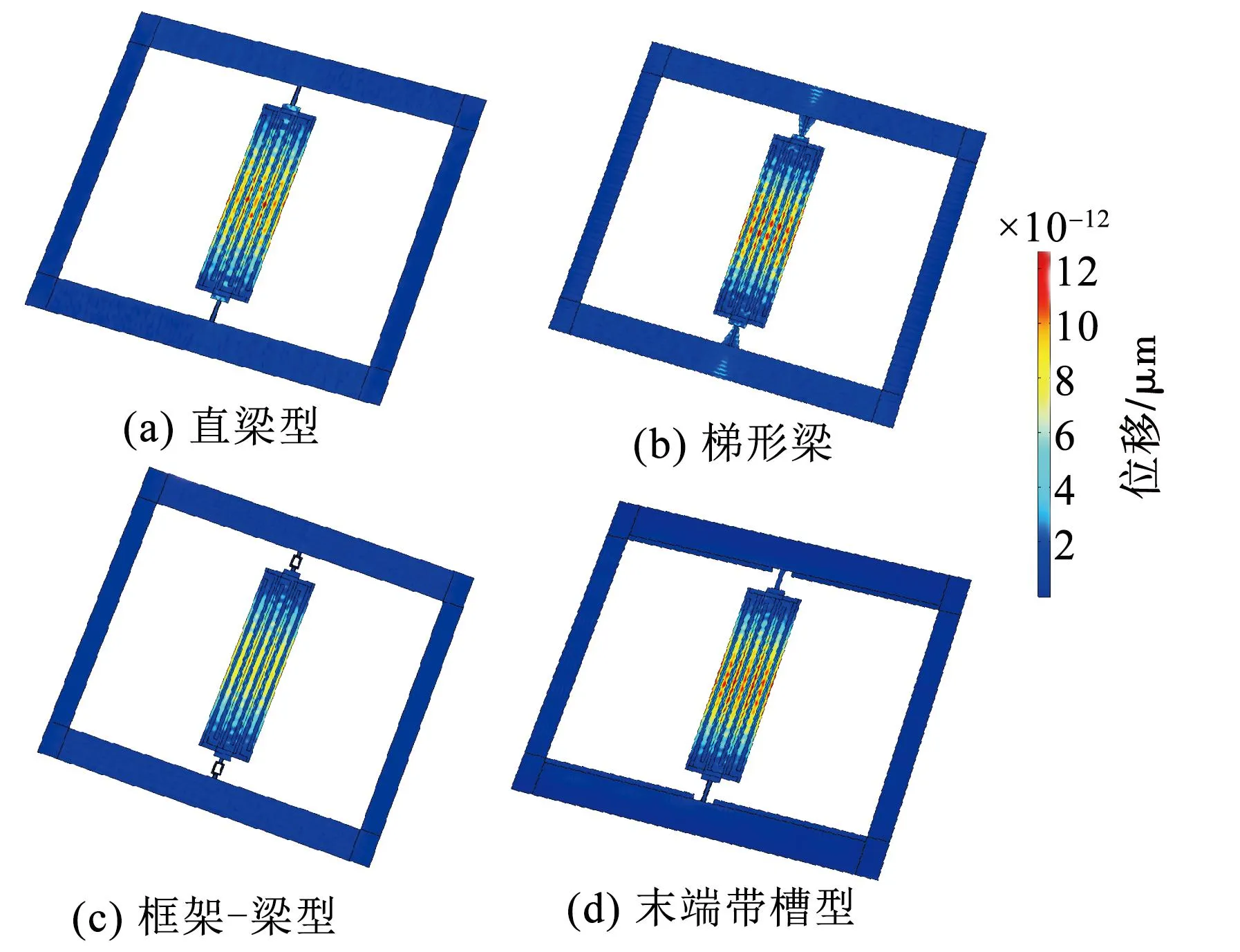
圖4 4種支撐錨結構下諧振器位移圖

由圖4可以看出,各種錨結構的支撐軸區域均存在一定位移,這表明有部分能量通過支撐錨泄露到襯底中而引起能量損耗。直梁型支撐錨的錨點處產生的位移幅度最大;其次是梯形梁支撐錨,位移以波紋形狀產生,代表能量泄露較嚴重;框架-梁型和末端帶槽型錨點處的位移最小,能量耗散最少。對4種錨結構下的器件進行頻域分析,得到導納曲線如圖5所示。由圖可見,4種錨結構下的諧振器諧振頻率在70.374 MHz附近,品質因數(Q)分別為1 221.9、1 244.9、1 338.1和1 292.4,其中框架-梁型的品質因數最大,其次為末端帶槽型。

圖5 4種支撐錨結構下諧振器仿真導納曲線

對上述結果進行分析可知,由于框架-梁混合結構具有較小的剛度和振幅,而末端帶槽型結構能夠在末端槽邊界處將泄露到襯底的聲波反射回去,從而降低了錨損。

為了進一步探究支撐梁與諧振體接觸面積對器件性能的影響,研究了框架-梁型錨結構下錨的寬度D分別為20 μm、30 μm、40 μm時器件的導納曲線,如圖6所示。這3種寬度下的諧振頻率都為70.372 MHz,品質因數分別為1 344.5、1 332.7、1 286.7。經分析可知,隨著支撐梁寬度的增加,諧振器品質因數降低,這是由于支撐梁與諧振體的接觸面積增加,導致更多的聲波能夠通過支撐梁擴散到襯底中而造成了更多損耗。由圖可見,3種寬度下的支撐梁導納曲線幾乎重合,表明支撐梁的寬度大小對諧振器雜散模態和主模態影響較小。

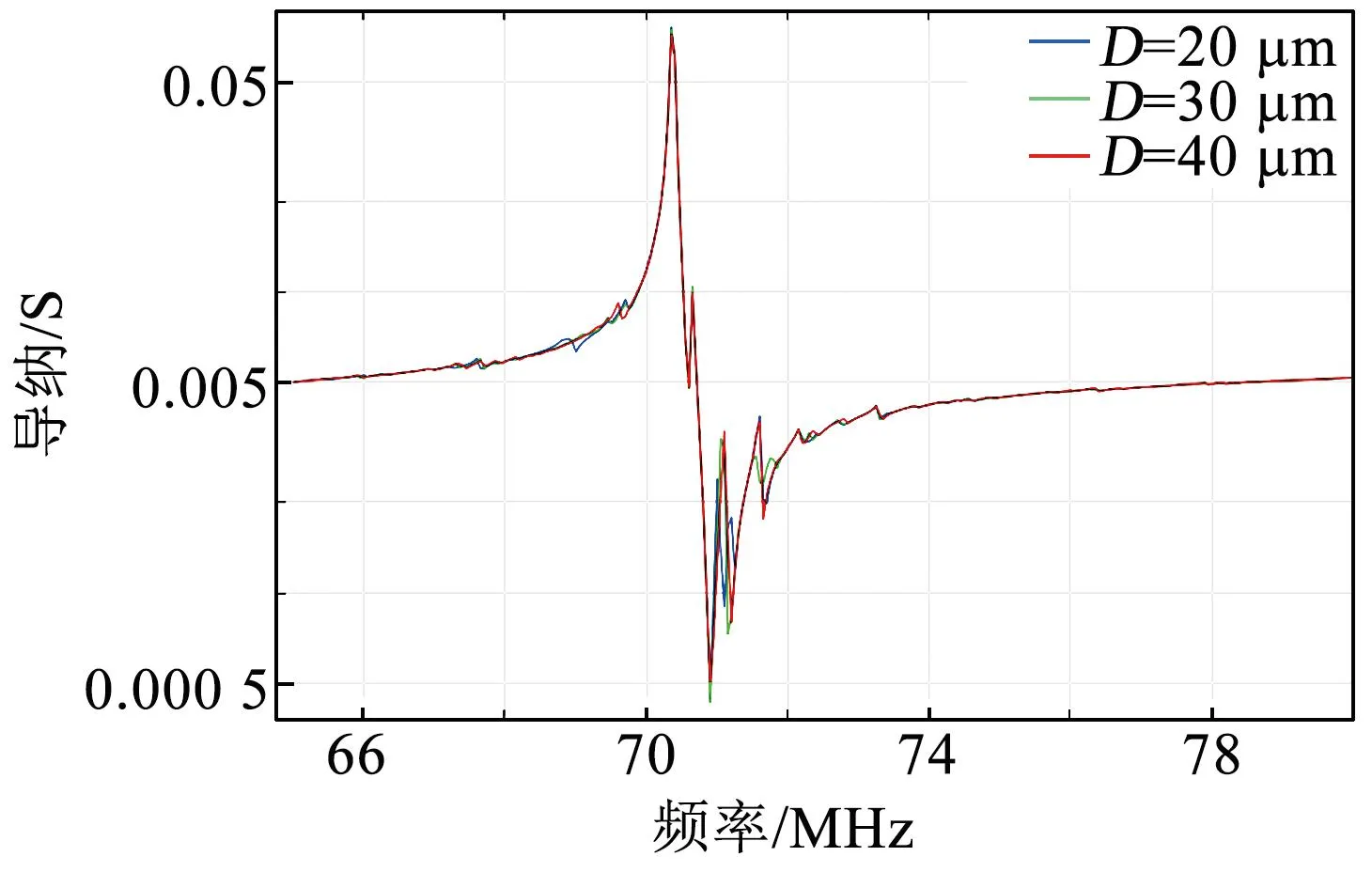
圖6 支撐梁寬度D為20～40 μm時器件導納圖

4 壓電材料的選擇

壓電材料的特性會影響到BAW器件的機電耦合系數和品質因數。從器件性能出發,選用壓電材料通常需要考慮壓電耦合系數、介電常數和聲速3個參數。其中壓電耦合系數直接決定了機電耦合系數大小,介電常數決定了器件阻抗水平,而聲速則與諧振頻率相關,通常在壓電層厚度一定時,聲速越大,諧振頻率越高。在諧振器設計過程中常用的壓電材料有壓電陶瓷(PZT-4)、氧化鋅(ZnO)、氮化鋁(AlN)等,其材料特性如表1所示。

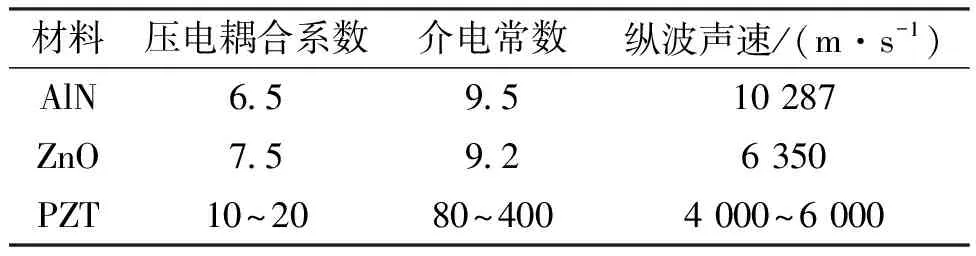
表1 幾種壓電材料的特性參數

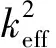
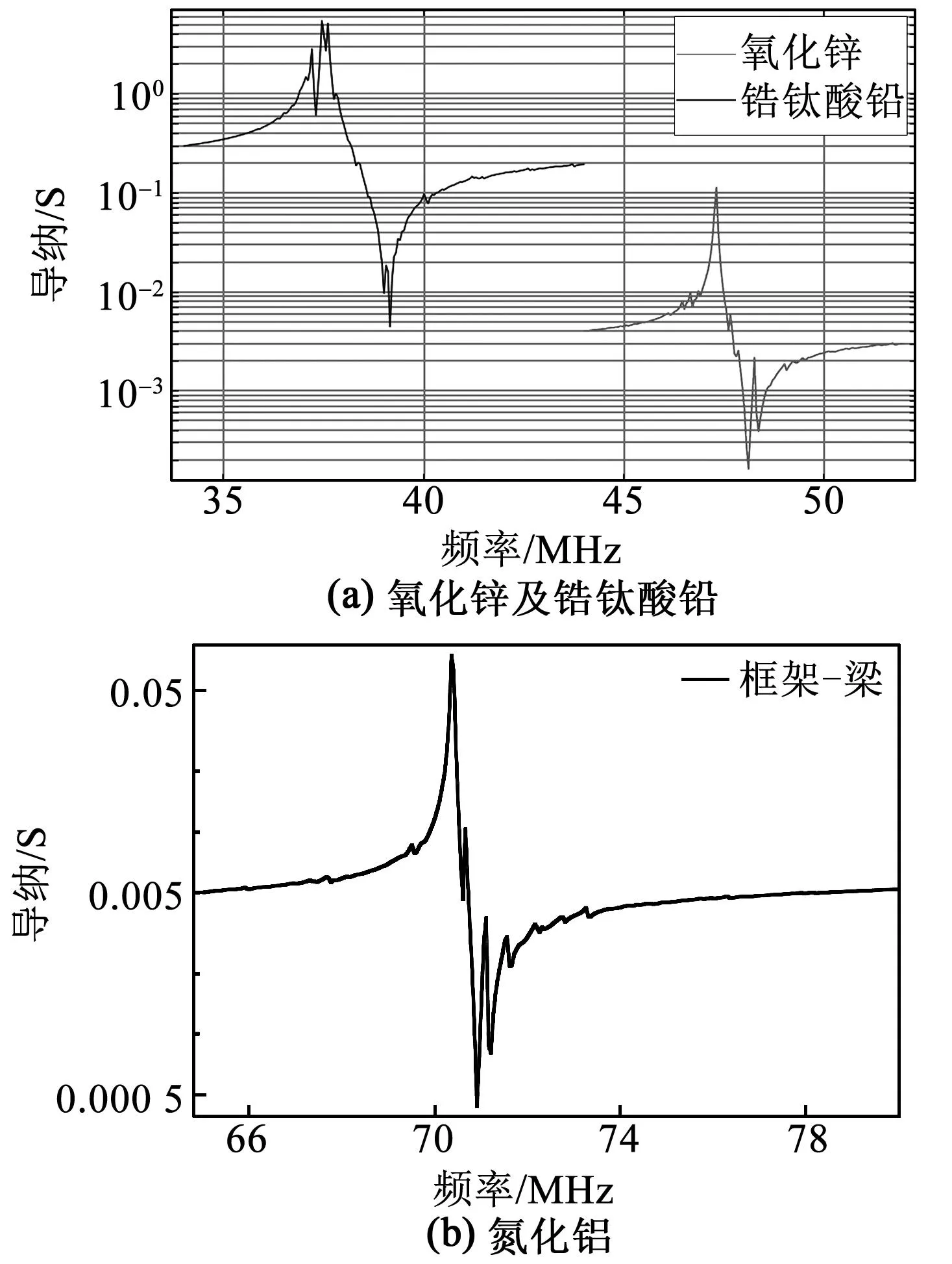
圖7 不同壓電材料下器件導納曲線

根據仿真結果可知, PZT-4具有最大的機電耦合系數,能夠實現更大帶寬的BAW濾波器,但應用該壓電材料時諧振器主模態附近的橫向雜散模態嚴重;ZnO具有相對較高的品質因數,且橫向雜散模態少于PZT;AlN因高聲速而具有最高的諧振頻率,主模態附近橫向雜散模態最少,能夠實現高頻濾波器。雖然PZT壓電性能好,但其性能易受到組分變化的影響,薄膜制備過程中難以保證其組分均勻;而ZnO不具備CMOS兼容性,相比之下,AlN具有與CMOS工藝相兼容的優點,且固有損耗較低,是制作BAW諧振器常用的壓電材料[14]。

5 等效MBVD模型仿真

根據上述仿真分析結果,本文選取帶有框架-梁支撐錨的氮化鋁BAW諧振器,建立的等效MBVD模型見圖1,參數如下:

(13)

C0=[2πf1(1+γ-1)Im(Z1)]-1

(14)

Cm=C0/γ

(15)

(16)

(17)

根據仿真所得導納曲線,由式(13)-(17)提取出MBVD模型中的各項參數,得到模型的等效電學參數如表2所示。利用ADS軟件建立等效電路模型并進行性能測試仿真,仿真的頻率范圍設定為68～74 MHz,步長設置為0.005 MHz,得到的S11參數曲線和導納Y11曲線如圖8所示。

表2 等效MBVD模型電學參數

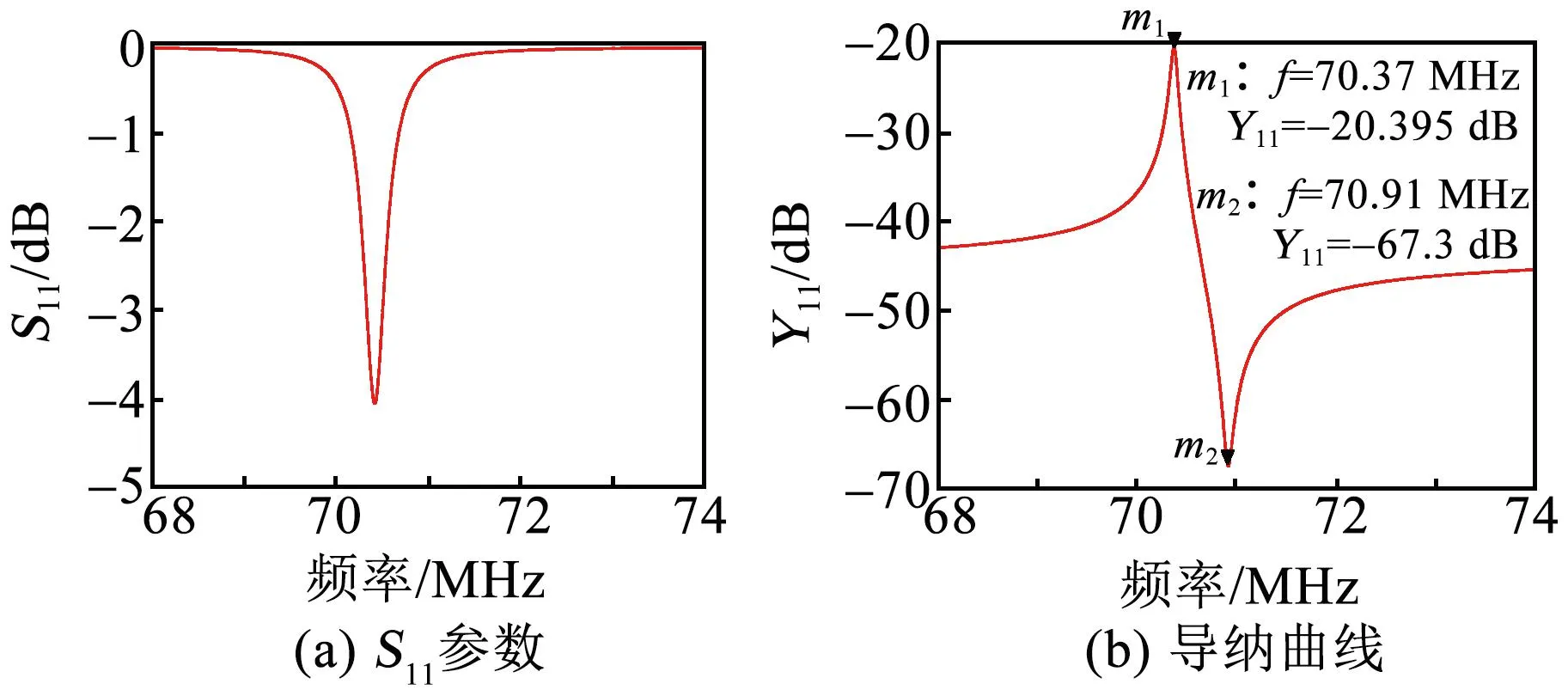
圖8 等效MBVD模型S11參數及導納曲線

S11參數反映了輸入回波損耗,該參數越小,表明回波損耗越低,能量傳輸效率越高[15]。由圖8可知,在BAW諧振器工作頻率處回波損耗非常小,在諧振區間外S參數接近0,表明器件插入損耗非常小。仿真導納圖所得參數與前述仿真結果貼合。

基于所設計的BAW諧振器單元,本文通過梯形級聯方式搭建了由其構成的BAW帶通濾波器并進行電學仿真,其中并聯BAW諧振器參數與上述所提取的諧振器電學參數相同。根據帶通濾波器工作原理及式(6),設置串聯BAW諧振器的Lm=24 099.356 9 nH,其余參數與表2相同,得到的一階帶通濾波器頻率響應曲線如圖9所示。由圖可知,濾波器為高頻窄帶濾波器,其通帶內插入損耗僅為-0.9 dB,3 dB帶寬為0.62 MHz,但其帶外衰減較小,通帶左側阻帶達到-5.872 dB,右側阻帶達到-7.457 dB,難以滿足帶通濾波器應用時的帶外衰減需求,因此需要增加諧振器的級聯數對帶外衰減進行優化。

圖9 梯形BAW帶通濾波器頻率響應特性曲線

通過增加上述BAW梯形濾波器的級聯階數,得到二階、三階BAW濾波器頻率響應曲線如圖10所示。由圖可知,隨著級聯階數的增加,濾波器的帶外衰減明顯增大,左側阻帶由-5.852dB增加到-22.907 dB,右側阻帶由-7.446 dB增加到-24.877 dB,表明帶外抑制得到改善,而通帶內插入損耗和帶寬隨級聯階數的增加,受到的影響較小,插入損耗>-1 dB,因此,所設計的BAW帶通濾波器適用于高頻窄帶應用范圍。

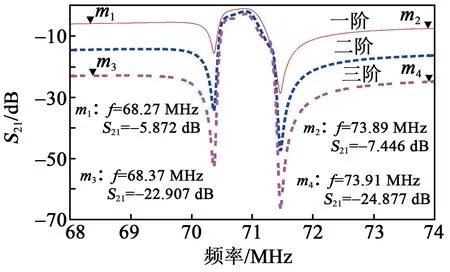
圖10 不同階數BAW帶通濾波器頻率響應曲線

6 結束語

BAW諧振器在應用過程中因存在諸多損耗機制而影響其品質因數,其中錨損是最主要的損耗機制之一。為了研究支撐錨結構對諧振器Q值的影響,本文對直梁型、梯形梁、框架-梁型及末端帶槽型4種支撐錨結構下的BAW諧振器進行建模仿真,并將器件激勵在蘭姆波S0模態下工作,得到諧振器諧振頻率在70.374 MHz附近,框架-梁型諧振器品質因數最高,達到1 338.1。同時還分析了不同支撐錨寬度下諧振器的諧振響應情況。經分析可知,隨著支撐梁寬度的增加,諧振器品質因數降低,但對諧振器雜散模態和主模態影響較小。此外,為了研究不同壓電材料對器件特性的影響,本文仿真分析了壓電材料為PZT-4、ZnO、AlN時器件的導納曲線,研究表明,PZT-4具有最大的機電耦合系數,ZnO具有相對較高的品質因數,AlN具有最高的諧振頻率。但考慮到AlN的固有損耗較低,且具有與CMOS工藝相兼容的優點,因此,本文建立了帶有框架-梁型支撐錨的AlN BAW諧振器的MBVD模型,并采用梯形級聯方式構建了BAW帶通濾波器進行仿真分析,最終得到插入損耗>-1 dB,頻帶在70.36～71.45 MHz的BAW濾波器模型。