基于多維矩特征聯合的K分布雜波參數估計

施賽楠，高季娟，李東宸

（1.南京信息工程大學電子與信息工程學院，江蘇南京 210044；2.中國船舶工業系統工程研究院，北京 100094）

0 引 言

復合高斯模型（Compound-Gaussian Model,CGM）［1］將海雜波建模為一個慢變紋理調制一個快變復高斯散斑的過程，已廣泛使用于海雜波建模中。在CGM 中，不同的紋理分布產生不同的海雜波幅度分布。典型的有，具有伽馬紋理的K 分布［2-3］，具有逆伽馬紋理的廣義Pareto 分布［4］、具有逆高斯紋理的復合高斯分布［5］和具有對數正態紋理的復合高斯分布［6］。這些雜波分布在研究雜波仿真、雜波抑制、最優或近最優檢測器設計等方面起著至關重要的作用。

目前，K分布已廣泛用于描述中低分辨率海雜波的幅度分布［2-3］。該分布的特性參數包括形狀參數和尺度參數，前者決定雜波的非高斯特性，后者反映雜波功率水平。通常，采用以下三大類方法獲得雜波參數的估計值。第一類，基于概率密度函數（Probability Density Function, PDF）的估計方法，比如最大似然（Maximum Likelihood，ML）估計法［7］和矩估計法（Method of Moment，MoM）［8］。ML估計精度高，但沒有顯式解析表達式且計算復雜度高?？紤]到實際雷達系統要求實時估計的要求，發展了結構簡單且快速估計的MoM 估計，比如2-4 階矩估計、1-2 階矩估計、分數階矩估計［9-10］等。此外，為了進一步挖掘矩信息，Yang 等人將原點矩偏導和原點矩之間的關系用于參數估計中［11］。針對小形狀參數下矩估計誤差大的問題，Blacknell等人提出zlog（z）期望的參數估計方法［12］。同時，在該方法上進行拓展，Hu 等人得到了zrlog（z）期望法［13］。第二類，基于累積分布函數（Cumulative Distribution Function, CDF）的估計方法，比如分位點估計法（Method of Percentile, MoP）［14-15］。Yu 提出基于三分位點估計器（Tri-percentile Estimator,TPE）［15］，兩個分位點比值用于估計形狀參數，第三個分位點用于估計尺度參數，適用于存在較多異常值的雜波環境中。由于K 分布存在貝塞爾函數，因而很難獲得分位點比值和形狀參數之間的函數關系，必須借助表格法獲得。第三類，基于非線性網絡的參數估計方法，引入人工智能網絡建立觀測值和參數之間的函數關系。Fernández 等人［16］提出先對數據功率進行歸一化處理，然后將直方圖作為神經網絡的輸入來估計形狀參數，只需單個網絡。但是，歸一化處理需要提前估計尺度參數，其誤差勢必會影響后續形狀參數的估計。因此，在設計估計器時，必須解決形狀參數和尺度參數獨立估計的問題。

為了進一步提高參數估計精度，本文提出了一種基于多維矩特征聯合的K 分布雜波參數估計方法。主要創新有以下三個方面。第一，聯合提取多個線性矩和對數矩，構建一個特征向量用于估計形狀參數，拓展矩信息的維度，進而提高數據信息的利用率。第二，將傳統基于統計分布的參數估計問題轉換為非線性優化問題，引入梯度提升樹（Gradient Boosting Decision Tree，GBDT）算法［17］，建立特征向量和形狀參數之間的非線性關系，提高估計精度。第三，精心設計矩特征，并推導證明特征向量與尺度參數相互獨立，并且二階矩只依賴于尺度參數，實現形狀參數和尺度參數的獨立估計。

1 K分布雜波的矩估計

1.1 K分布雜波

根據海雜波的物理散射機理，海雜波可表述為一個慢變分量調制一個快變分量，即

式中：τ稱為紋理分量，是一個正的隨機變量，由大尺度的涌浪產生；u稱為散斑分量，服從零均值、單位方差的復高斯分布，由小尺度的毛細波產生。在CGM 中，不同的紋理分布會產生不同的雜波幅度分布。當紋理服從伽馬分布時，海雜波幅度x=服從K分布。K分布的PDF表達式為

式中，Γ(·)為伽馬函數，Kv-1(·)為v-1 階的第二類修正Bessel 函數，v為形狀參數，b為尺度參數。形狀參數決定分布的非高斯性，尺度參數與雜波功率相關。

根據式（2），計算出r階矩為

式中，E為期望運算符。通常，理論矩是未知的，需要通過獲取實際環境中的N個樣本獲得。假設N個樣本x1,x2,…,xN服從K分布且相互獨立，則樣本矩為當樣本數目N趨向于無窮時，樣本矩等于理論矩。

1.2 估計器的互補性

在實際雷達探測場景中，通常需要快速獲得K分布的參數估計值。因而，矩估計方法得到了廣泛的應用。理論上，MoM 估計可使用任意兩個矩來估計形狀參數和尺度參數。在式（3）中，令r=2，則

可見，二階矩只決定于尺度參數b。根據式（4），得到尺度參數的估計為

因此，矩估計的重點在于如何獲得形狀參數的估計。典型地，2-4 階矩估計法（MoM 2-4）、1-2 階矩估計法（MoM 1-2）的形狀參數估計分別為［8］

此外，為了更好地擬合重雜波拖尾的雜波，文獻［13］采用對數矩，稱為zrlog（z）期望法，其形狀參數的表達式為

式中，z=x2為雜波功率，ψ(·)為Digamma 函數。同樣，zrlog（z）期望法無法獲得形狀參數的顯式解析表達式，只能借助數值法求解。

下面，討論不同矩估計器的形狀參數估計性能。由于尺度參數估計方法一致，采用形狀參數的相對均方根誤差（Relative Root Mean Square Error，RRMSE）作為衡量指標：

式中，v和?分別為形狀參數的真實值和估計值。圖1 給出了不同形狀參數下的6 種矩估計器的RRMSE 曲線。在圖1（a）中，低階矩MoM 1-2 的估計誤差明顯小于高階矩MoM 2-4 的估計誤差。因而，實際矩估計器的矩階數一般不會高于4。相對于MoM 1-2 估計器，MoM 1-2-3 估計器增加一個高階矩后，在中等形狀參數下有一定的性能提升。這意味著，合理地增加矩的個數是一種提升估計性能的潛在途徑。在圖1（b）中，當形狀參數v＜2 時，對數矩的估計誤差明顯小于矩估計。但是，當形狀參數v＞10 時，情況正好相反。此外，不同階數r明顯影響估計性能。當r＜1 時，適合估計具有小形狀參數的雜波；當r＞1 時，適合估計具有大形狀參數的雜波。從整體上來看，MoM 估計器在形狀參數較大時的估計性能較好，而zrlog（z）估計器在形狀參數較小時的估計性能較好，兩種估計器具有一定的互補性。因此，可以考慮將兩者的優勢結合起來，以降低整體的參數估計誤差。

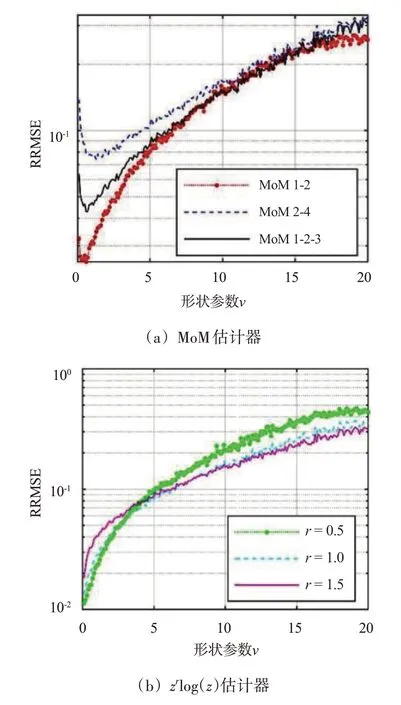
圖1 不同估計器的性能互補性分析

2 基于多維矩特征聯合的參數估計方法

2.1 非線性參數估計框架

事實上，海雜波幅度分布的參數受到多種因素的影響［1-2］，主要包括雷達工作參數和實時海洋環境參數。雷達工作參數一般有距離分辨率、擦地角、極化方式等。在高分辨率小擦地角下，海雜波的幅度分布明顯偏離高斯分布，其分布的形狀參數變小。海洋環境參數包含風速、風向、海況、溫度等多種氣象因素。通常，氣象環境是隨著時間不斷變化的。不同環境下采集的雜波參數特性是不同的。因此，一種可靠有效的手段是收集當前環境下的雷達回波后實時估計雜波的參數。此外，在時間上，海雜波時間序列呈現出短時平穩而長時非平穩特性。在空間上，海雜波具有局部均勻而整體非均勻的特性。然而，通常要求用于雜波參數估計的樣本是獨立同分布的，這意味著只有局部區域中短時的雜波序列可用于參數估計。幸運的是，高分辨雷達一旦開機后，可收集大量的局部短時雜波序列。因此，在大場景雜波環境下，需要對不同空間的雜波進行劃分，實時估計雜波特性。

對于K 分布雜波，需要估計形狀參數和尺度參數。尺度參數反映了雜波的平均功率水平，可根據式（6）中的幅度二階矩，獲得其估計值。形狀參數反映了雜波的非高斯特性，更能表征雜波的本質，并且其與最優相干檢測器相關。因而，亟需解決的是K分布雜波的形狀參數估計。

本質上，矩估計法是通過幅度分布的PDF 建立了兩個線性矩和形狀參數之間的函數關系進行參數估計的。這種方法的核心在于找到函數關系，最終估計器是否存在顯式解析表達式與采用的兩個矩戚戚相關，比如式（7）中的MoM 2-4 和MoM 1-2。啟發于這種思路，本文提出了一種基于多維矩特征聯合（Multidimensional Moment Feature Combination,MMFC）的估計器框架，通過豐富估計器可用信息以提升形狀參數的估計性能，如圖2所示。首先，提取了海雜波時間序列c（n）,n=1,2,…,N中的矩特征，包含線性矩特征和對數矩特征兩大類。其次，聯合所有的特征，構成一個特征向量ξ。在高維特征空間中，該向量凝聚了海雜波時間序列的顯著特征。然后，K分布參數估計問題轉換為高維空間中的一個非線性優化問題。該優化問題最終找到一個最優的非線性函數F，建立特征向量ξ和形狀參數v之間的函數映射關系，實現形狀參數估計。最后，根據式（6）中的幅度二階矩，獲得尺度參數的估計。

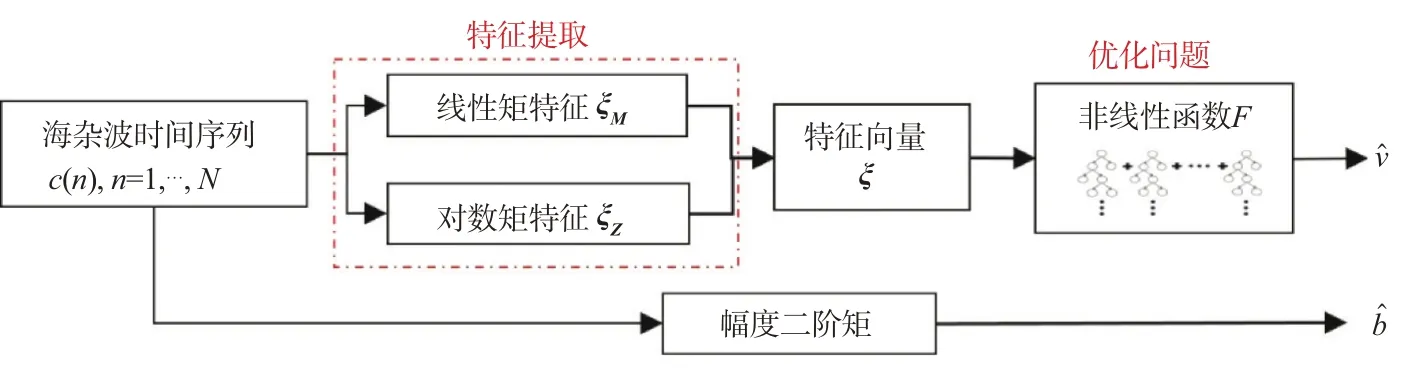
圖2 MMFC估計的流程圖

MMFC 估計法的核心在于特征提取和非線性函數獲取。由于K 分布是雙參數模型，式（3）中的原點矩往往由兩個參數決定。但是，在實際參數估計中，為了降低估計誤差，往往要求兩個參數的估計是獨立的。這意味著提取的特征必須只包含單個參數的信息。因而，特征設計的首要原則是必須只依賴于形狀參數，完全獨立于尺度參數。并且，如何從海雜波序列中提取有效的特征，這也是特征提取的難點和重點。在傳統矩估計中，雖然用了兩個矩，但實際上只有單個矩比值，屬于一維優化問題。根據雜波分布的PDF，一般都可以尋找到非線性函數，且在特殊情況下具有顯式解析表達式，如MoM 2-4 估計器。不同于傳統矩估計，特征向量包含了多個矩的信息，需要在三維甚至更高維的特征空間中尋找非線性函數F。因此，以尋找與真實形狀參數誤差最小的F為目標，可構建如下的最優化問題：

式中，F（.|v）表示只依賴于v的高維非線性函數且?，高維空間維度取決于特征向量的維度。通常，為了提升估計性能，需要聯合更多的矩特征，勢必會增加非線性函數的維度。因此，式（11）的優化問題很難從理論上獲得具體解析函數表達式。此外，基于多維特征的估計方法是一個開放的框架，可以自由地設計特征以及尋找非線性函數。同時，該框架不局限于K 分布雜波，不依賴于雜波的概率分布，后續可用其他不同的雜波分布。

2.2 多維矩特征提取

在海雜波分布參數估計中，可用的信息全部來自于當前局部區域獲得的海雜波時間序列。通常，從海雜波時間序列中獲得統計矩，用于估計雜波分布的形狀參數和尺度參數。本文將反映雜波特性的統計特征，統稱為特征。相對于海雜波時間序列，特征凝聚了雜波特性，大大減少了數據的存儲空間。在這種情況下，如何提取有效特征是估計的核心。目前，K分布下發展了大量的矩估計器，這表明統計矩是一種有效的特征。

那么，下一步是如何設計矩特征。需要指出的是，在式（3）中，除了二階矩，其他任意r階矩由尺度參數和形狀參數同時決定。若直接使用矩特征，需要同時估計尺度參數和形狀參數，因為這兩者是相互關聯的。這無疑大大增加了參數估計的困難。目前，有兩種途徑可以解決上述問題。第一種途徑，先采用二階矩估計尺度參數，然后將海雜波時間序列的功率除以尺度參數，獲得歸一化的海雜波時間序列，去除尺度參數影響［17］。這種方式易于尋找特征，但尺度參數的估計誤差勢必會進入形狀參數的估計中，從而降低估計性能。第二種途徑，設計不依賴于尺度參數的特征，比如MoM 2-4中四階矩比二階矩的平方，完全去除尺度參數和形狀參數的相關性，使兩個參數的估計誤差不再相互影響，有利于提升估計性能。但這就需要設計者具有一定的先驗知識去尋找具體的特征。

為了減少估計性能的損失，本文采用第二種途徑。假設存在a,c,d階的3個矩，矩比值定義為

當a=c+d時，矩比值僅取決于形狀參數v，獨立于尺度參數b。

綜合考慮現有的MoM 估計器和式（12）特性，本文精心提取了7個矩比值，構成一個線性矩向量

該線性矩向量凝聚了0.5 階、1.5 階、2.5 階、3.5 階分數矩和1 階、2 階、3 階、4 階矩的信息，豐富了信息的多樣性，同時拓展了信息的維度。

同樣地，根據式（9），可證明對數矩比值只與形狀參數有關。因此，本文提取了3個對數矩比值特征，構成一個對數矩向量

考慮到對數矩和線性矩估計器兩者的互補性，將兩個矩向量聯合，構建一個高維特征空間。相應地，得到一個10維的特征向量

顯然，該特征向量ξ只與形狀參數v有關。由于式（12）和式（9）中存在伽馬函數和Digamma 函數，理論上很難推出ξ和v之間的顯式解析表達式。

2.3 非線性函數獲取

在高維特征空間中，式（11）的優化問題需要找到一個高維函數關系，實現從特征向量中估計出形狀參數，且該函數必須保證估計值與真實值之間的誤差最小。理論上，存在這樣的高維函數關系。但是，由于高維函數的非線性和復雜性，實際上很難給出這樣的數學解析表達式。因此，本文引入模式識別里的GBDT算法［17］，獲得非線性函數F的最優表達式。

GBDT 算法是一種以分類回歸樹（Classification And Regression Tree, CART）為基學習器的集成學習算法。它能夠學習輸入向量中蘊含的多維信息，建立輸入向量和真實值之間的復雜函數關系，在小樣本數據上具有較好的估計性能。假設存在M棵CART 樹，每棵樹的深度為D，級聯構成GBDT模型。對于任意一棵樹，按照損失函數的最小值進行迭代更新參數。損失函數定義為平方誤差，即

式中，f(·)表示某棵CART 樹的函數。與式（11）中的優化問題一致，所有的CART 樹都尋找與真實形狀參數值誤差最小的函數。最終，將M棵CART樹的結果累加獲得最終的估計結果。當GBDT 的輸入為式（15）中的特征向量ξ時，最終輸出為

式中，fM(·)表示第M棵CART 樹的參數函數。因此，借助GBDT 算法，fM(·)可以作為式（11）中最終優化函數F的近似解。當然，后續也可以采用其他的算法，獲得優化問題的最優解或近似最優解。

下面，問題的關鍵是如何獲得GBDT 模型的參數。這就需要從大量的海雜波時間序列中自主學習模型的最優參數。假設訓練集Ω包含Q個特征向量ξi,i= 1,2,…,Q和相對應的真實形狀參數值vi,i= 1,2,…,Q，簡記為

需要指出的是，訓練集樣本需要盡可能地覆蓋不同形狀參數，保證建立較為穩健的特征向量和形狀參數之間的關系。此外，需要保證不同形狀參數下的樣本數量是足夠的，能深入挖掘到特征向量所包含的形狀參數信息。

圖3 給出了GBDT 模型的訓練過程，用于獲取模型的最優權重參數，具體步驟如下。

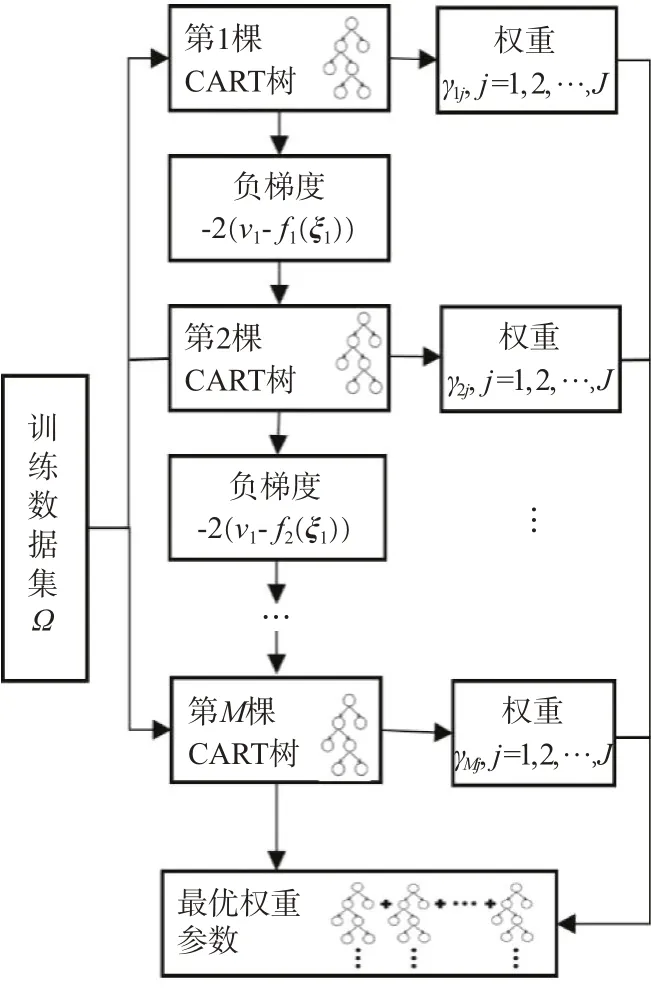
圖3 GBDT模型訓練過程

步驟1：初始化

對于輸入的訓練集Ω，初始化參數為式中，γ表示使損失函數達到最小的常數。

步驟2：生成第m棵CART樹

對于第i個樣本，計算損失函數的負梯度

由此，得到J個葉節點以及其對應的葉節點區域Rmj,j= 1,2,…,J。然后，計算第j個節點的最佳殘差擬合值

最后，生成第m棵CART樹的參數函數

式中，ρ∈[0,1]為學習率，避免過擬合現象。當ξi∈Rmj成立時，I（ξi∈Rmj）取值為1，反之為0。

步驟3：生成第M棵CART樹

重復步驟2，直到生成第M棵CART樹。最終，GBDT的輸出為

至此，獲得給定訓練樣本下的GBDT 模型的最優權重參數，完成式（11）中的最優化問題求解。

3 實驗結果與性能分析

3.1 GBDT參數設置

事實上，形狀參數的估計精度在很大程度上依賴于GBDT 模型的參數。通常，GBDT 模型主要分為結構參數和學習參數兩大類。結構參數決定了GBDT模型的結構，比如CART樹的數目M，每棵樹的最大深度D，學習率ρ等。學習參數需要從訓練集中學習獲得，比如葉子節點數J，葉子節點對應的最佳殘差擬合值等。當訓練集更改時，學習參數必須重新從訓練集中學習獲得，即高度依賴于數據。然而，結構參數對數據的依賴度較小，可以提前設置。理論上，結構參數設置得越大，即聯合更多和更深的基分類器，可以提高估計性能。但同時也帶來了過擬合和計算量高的問題。因此，有必要研究如何設置合理的結構參數。

圖4 給出了不同結構參數下估計器的平均RRMSE 曲線，其中平均RRMSE 為形狀參數從0 到20 之間的平均誤差值。在圖4（a）中，隨著CART樹的數目增加，平均RRMSE 的值逐步減少。這表明多個弱分類器聯合后，確實可以提高估計性能。但是，這種性能增加不是無止盡的。當M＞100后，估計性能趨于穩定。在圖4（b）中，隨著樹的深度D的增加，平均RRMSE 的值呈現先下降后上升的趨勢。這說明較大的深度可以提升估計性能，但過大的D值，導致GBDT 算法存在過擬合的問題。類似地，在圖4（c）中，隨著學習率ρ的增加，導致GBDT 算法過度依賴于先前的數據特性而性能降低。因此，綜合考慮性能和計算量，在后續的實驗中，設置M=200，D=15，ρ=0.1。

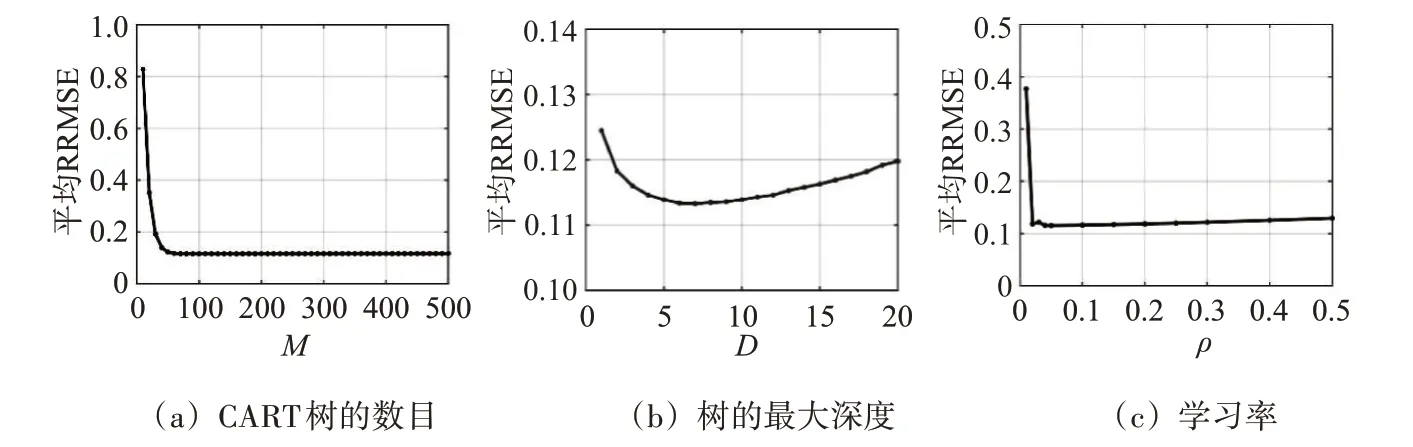
圖4 結構參數對估計器性能的影響

3.2 仿真數據結果

除了結構參數，GBDT 的估計性能還受到學習參數的影響。GBDT 模型需要根據當前的數據不斷更新學習數據本身包含的形狀參數和矩特征之間的關系。因此，需要合理地設置訓練集，以保證GBDT 模型估計性能的廣泛性和優越性?？紤]到K 分布的特性，設置形狀參數的范圍從0.1 到20，間隔為0.1 均勻取值。由于矩特征不依賴于尺度參數，因而尺度參數可任意取，比如設定為1。對于每個給定的形狀參數v，生成長度為104服從K分布的海雜波時間序列，按照式（13）和式（14），提取對應的線性矩特征和對數矩特征，最終構成式（15）中的特征向量。該特征向量和真實的形狀參數，構成一個樣本。為了增加樣本數目，該過程重復1 000次。因此，對于式（18）的訓練集，總樣本數為Q=200 000，用于訓練GBDT模型的最優學習參數。

圖5 給出了5 種估計器的RRMSE 誤差曲線。隨著形狀參數的增加，所有誤差曲線呈現出增大的趨勢。這是因為在大形狀參數下K 分布海雜波趨向于高斯分布，導致PDF 曲線之間差異性變小。MoM 1-2 估計器［8］性能整體優于MoM 2-4 估計器［8］，再次驗證了低階矩在估計性能上的優勢。然而，zlogz估計器［12］性能與MoM 1-2 估計器［8］接近，并且在形狀參數v＜2 時，其估計誤差最小。為了提升估計器性能，TPE估計器［15］的一個分位點設置為0.9。該估計器在形狀參數v＜2 時具有較好的性能，但在形狀參數較大時，性能損失嚴重。這是由其估計器本身特性決定的。不同于矩估計，分位點估計只采用了3個分位點的信息，因而信息量非常有限。在大形狀參數情況下，存在一定的性能損失。但這些有限的信息，在異常環境下，具有較好的抗噪聲性能。從整體上來說，本文所提的MMFC 估計器的平均RRMSE 值最小，具有最佳的估計性能。相較于MoM 1-2［8］和zlog（z）估計器［12］，MMFC 估計器不僅在小形狀參數（v＜2）時獲得更精準的估計結果，并且大大降低了在大形狀參數（v＞10）下的估計誤差。這種性能優勢主要得益于多個線性矩特征和對數矩特征的聯合使用，集成了線性矩估計和對數矩估計的優勢。

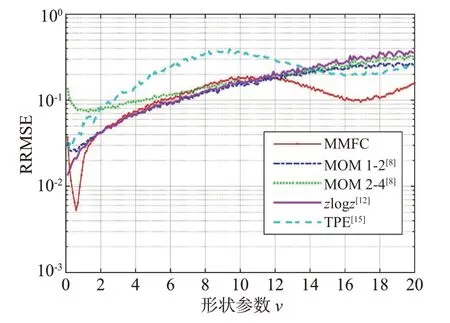
圖5 不同形狀參數下估計器性能對比

為了更加量化性能對比結果，表1 列出了不同形狀參數區間下，5 種估計器的平均RRMSE值。從整體來看，即ν∈(0,20]，所提估計器的平均RRMSE 最小。相對于MoM 1-2 估計器［8］、MoM 2-4 估計器［8］、zlogz估計器［12］和TPE 估計器［15］，所提MMFC 估計器分別有23%，34%，33%，48%的估計性能提升。 當形狀參數非常小時，即ν∈(0,0.5]，K 分布海雜波完全偏離高斯分布，其概率密度函數表現出嚴重的重拖尾現象。通常，這種雜波出現在高海況、低擦地角條件下。此時，MMFC 估計器僅次于最優的zlogz估計器，具有部分性能損失。 當形狀參數較小時，即ν∈(0.5,2]，此時K 分布海雜波具有重拖尾現象，出現在中高海況下，這也是大多數雷達工作的環境。相對次最優zlogz估計器［12］，MMFC 估計器的性能最優，具有19%的性能提升空間。當形狀參數中等大小時，即ν∈(2,10]，此時K 分布海雜波較為平穩，出現在低中海況下。除了TPE 估計器［15］存在較大的性能損失，剩下的4 種估計器性能接近。當形狀參數較大時，即ν∈(10,20]，K 分布海雜波接近高斯分布，往往出現在低海況下或遠海區。所提估計器能夠充分利用多個矩的信息，相對于次優MoM 1-2 估計器具有36%的性能提升。綜上，所提MMFC 估計器具有最佳的綜合性能，有望應用于不同的雜波環境下。

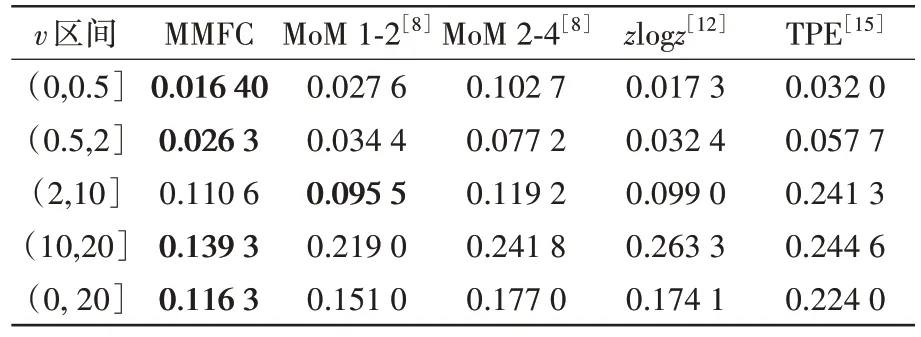
表1 不同形狀參數區間下的平均RRMSE值

3.3 實測數據結果

在仿真實驗中，RRMSE 可以用來準確地衡量形狀參數的估計誤差。但是，該指標要求已知真實形狀參數，這在實際探測環境下是不可能實現的。因此，當用實測數據評估性能時，采用KS 距離（Kolmogorov-Smirnov Distance,KSD）

式中，C(·)表示K 分布的CDF。在實際雜波環境中，K 分布雜波的所有真實參數都是未知的。此時，雜波序列真實的CDF 通常用經驗CDF 代替。因此，KSD 反映了由參數估計值得到的經驗CDF與真實CDF 之間的差值大小。KSD 值越小，表明擬合誤差越小，估計精度越高。

實測數據來自X 波段Fynmeet 雷達于2006 年8 月1 日采集的數據［18］，文件名為TFC15_004。該雷達架設在岸邊，工作在VV 極化下的駐留模式，距離分辨率為15 m，脈沖重復頻率為5 kHz，探測范圍距離岸邊3 km到4.4 km。圖6（a）畫出了時間-距離的雜波幅度圖，呈現出明暗交替的“斑馬”條紋現象。顏色越亮，表明雜波幅度值越高，反之雜波幅度越低。區域A 包含大量的亮點，雜波幅度起伏較大。區域B同時包含亮點和暗點，雜波幅度起伏中等。區域C包含大量的暗點，雜波幅度起伏較小。這3個區域作為不同雜波特性的典型區域，用于驗證不同估計器的性能，結果如圖6（b）～（d）所示。

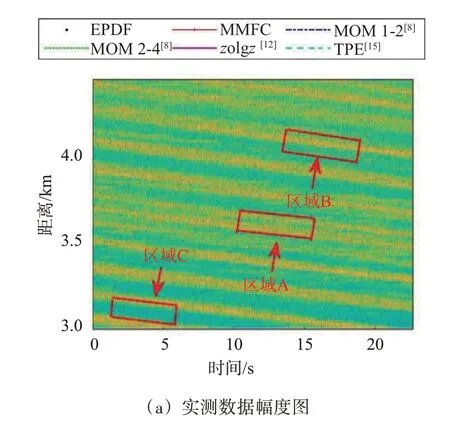
圖6 Fynmeet數據上5種估計器的擬合結果

表2 列出了各個估計器的形狀參數估計值和KSD 值。在區域A 內，形狀參數v的值較小，雜波具有很強的非高斯性。MMFC 估計器的KSD 值最小，其次是zlogz估計器［12］，剩下3 種估計器都遭受了較為嚴重的性能損失。在區域B內，形狀參數的值中等，雜波幅度較為均勻。因而，5 種估計器的KSD 值較為接近，但MMFC 估計器的KSD 值仍是最小的。在區域C 內，形狀參數v的值較大，雜波趨向于高斯分布。MMFC估計器的估計精度最高，zlog（z）估計器［12］的估計誤差最大。由此可見，5 種估計器在實測數據3 個區域內的參數估計結果和仿真實驗的結果一致。并且，所提MMFC 估計器在3 個區域內都實現了最佳的擬合，這表明MMFC估計器具有較好的穩健性，能適用于不同的K 分布雜波環境。

表2 3個典型區域雜波擬合值

4 結束語

本文主要研究了K 分布雜波的參數估計方法。不同于基于概率密度函數的矩估計法，將參數估計問題轉換為高維特征空間中的非線性最優化問題。因此，提出了一種基于多維矩特征聯合的估計方法，豐富了參數估計的信息量。所提出的估計器具有穩健的估計性能，能運用于實際復雜雜波環境。此外，本文給出的是一種新的參數估計框架，后續可根據雜波特性深入研究特征提取和非線性函數獲取的問題。