光伏光熱墻體結構優化模擬研究

李佳琪, 劉 芳, 蔡慶峰, 王曉夢, 王澤林

(山東建筑大學熱能工程學院,山東濟南250101)

1 概述

隨著經濟發展和城市建設不斷推進,化石能源消耗持續增加。在全球范圍內,建筑能耗約占能耗總量的40%左右。為減少建筑能耗,眾多學者對太陽能利用進行了廣泛研究。太陽能空氣集熱器是太陽能利用的主要裝置之一,太陽能光伏光熱系統能夠將接收的太陽能同時轉化為電和熱[1-3]。

特朗伯墻是一種依靠墻體獨特的構造設計,無機械動力、無傳統能源消耗,僅依靠被動式收集太陽能為建筑供暖的集熱墻體。特朗伯墻由法國太陽能實驗室主任Trombe教授及其合作者首先提出并實驗成功,因此稱為Trombewall(特朗伯墻)。眾多學者基于特朗伯墻原理進行了實驗和模擬研究。Peng等人[4-5]研究了不同通風模式下的通風光伏立面墻的電熱性能,并針對不同天氣條件提出了適當的運行策略。實驗結果表明,通風模式可降低光伏組件的工作溫度,從而提高系統的發電效率。虞麗丹[6]對光伏光熱墻體系統流道內空氣流動的傳熱特性進行分析,結果表明,可以在允許的范圍內盡量增加流道的高度,但流道的寬度一般不宜大于70 mm;當高寬比大于30時,更有利于流道內的流動傳熱。Alberto等人[7]認為對雙層幕墻效率影響最大的是氣流路徑,雙層立面結構能夠最大限度降低氣隙內部空氣溫度。Preet等人[8]發現合理的空氣流道和風速組合可顯著提高光伏系統的電功率輸出。Zhu等人[9]提出了一種設置雙層相變材料板的特朗伯墻,結果表明,相變材料板可改善建筑圍護結構的全年熱性能。Ling等人[10]和Meng等人[11]證明了相變材料能夠降低建筑能耗、提高用能效率。Preet等人[12]分析指出,將相變材料與光伏光熱系統結合可提高發電效率和熱效率。

研究表明,光伏板溫度上升1 ℃,光電轉換效率下降0.3%～0.5%。而風道與光伏板的結合既有利于光伏板降溫,也可以拓寬光伏光熱系統在建筑中的應用。本文提出4種光伏光熱墻體,針對夏季工況,對4種光伏光熱墻體的出口溫度、空氣得熱量、光伏板表面溫度進行模擬。

2 物理模型

光伏光熱墻體高×寬×厚為1 700 mm×1 000 mm×304 mm。由室外到室內依次為:玻璃蓋板、光伏板、空氣通道、磚墻。玻璃蓋板高×寬×厚為1 700 mm×1 000 mm×4 mm。光伏板長×寬×厚為1 000 mm×700 mm×4 mm,安裝在墻體高度中間部分。空氣通道進、出口截面尺寸均為1 000 mm×100 mm。磚墻高×寬×厚為1 700 mm×1 000 mm×200 mm,當設置相變材料時磚墻厚度含相變材料厚度(60 mm)。4種光伏光熱墻體物理模型見圖1。各模型均由玻璃蓋板、光伏板、空氣通道、磚墻組成,模型1、2的光伏板緊貼玻璃蓋板內側,模型3、4的光伏板置于空氣通道中間,模型2、4在磚墻一側增設相變材料層。相變材料選用石蠟,光伏光熱墻體各種材料的熱物性參數見表1。空氣密度由數學模型計算得到。

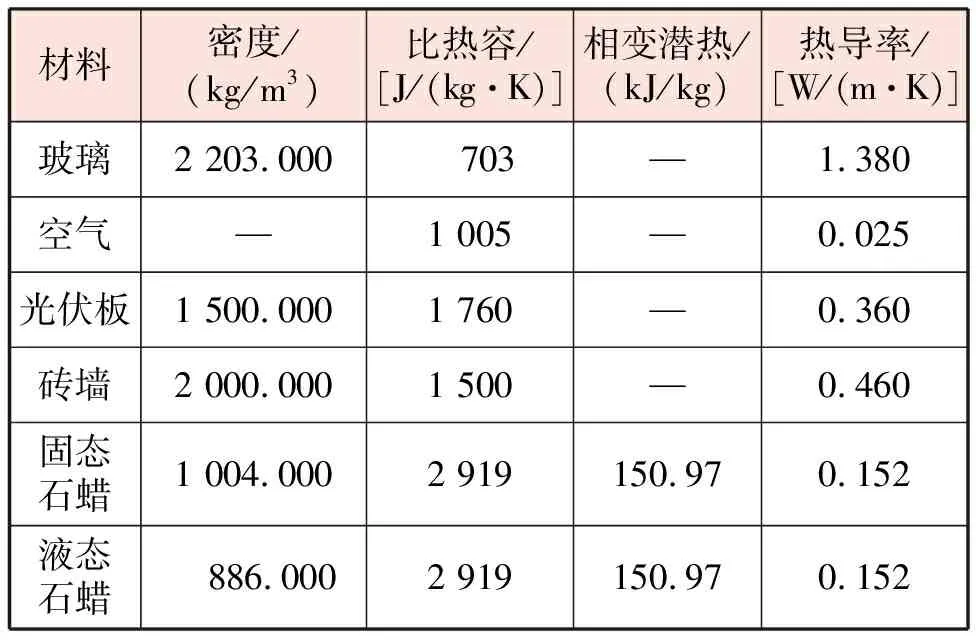
表1 光伏光熱墻體各種材料的熱物性參數

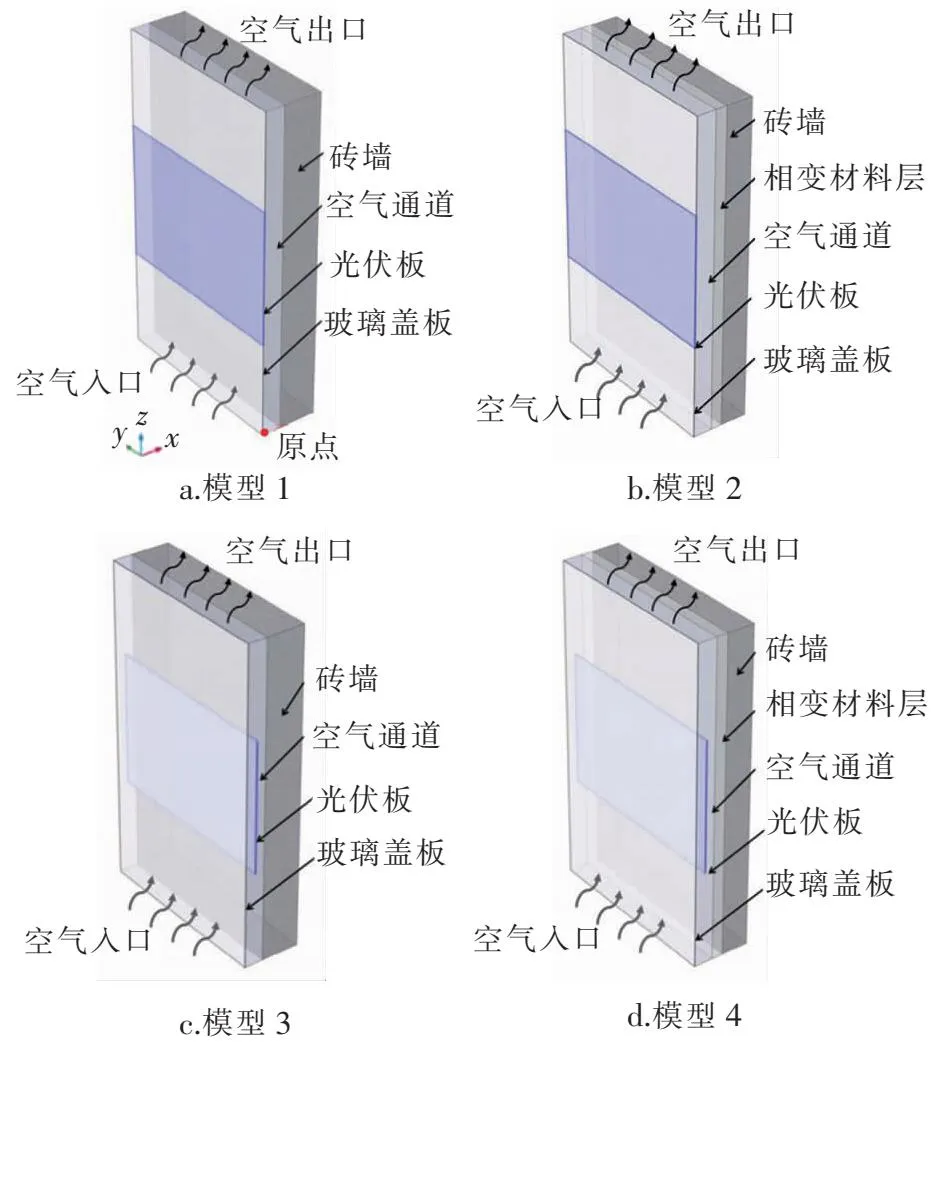
圖1 4種光伏光熱墻體物理模型

3 數學模型

3.1 主要數學方程

光伏墻體的熱量傳遞主要是沿著墻體厚度方向。為簡化計算,進行以下設定:光伏墻體內各層材料均為各向同性。相變過程中,相變材料除了密度發生變化外,比熱容、熱導率均不變。不考慮相變材料固液兩相之間的對流。忽略光伏墻體各層材料之間的接觸熱阻。

① 空氣層

連續性方程:

div(ρu)=0

(1)

式中 div——散度

ρ——空氣密度,kg/m3

u——空氣速度矢量,m/s

動量方程:

ρ(udivu)=-divp+divμ(gradu)

(2)

(3)

(4)

式中u——空氣速度分量,m/s

p——空氣壓力,Pa

μ——空氣動力黏度,Pa·s

grad——梯度

k——湍流動能,J

μT——湍流黏性系數,Pa·s

σk——模型常數,取1.00

Pk——湍流動能生成項

ε——湍流耗散率

σε——模型常數,取1.30

C1——模型常數,取1.44

C2——模型常數,取1.92

② 磚墻傳熱方程

磚墻接收太陽能,熱量的傳遞過程主要為導熱,傳熱方程為:

(5)

式中ρw——墻體材料密度,kg/m3

cw——墻體材料比熱容,J/(kg·K)

θw——墻體材料溫度,K

t——時間,s

λ——墻體材料熱導率,W/(m·K)

Q——熱源項,指吸收的太陽輻射熱,W/m3

光伏板吸收太陽輻射后,與空氣層內空氣對流傳熱。玻璃蓋板外表面與室外空氣對流傳熱,玻璃蓋板內表面與空氣層內空氣對流傳熱,玻璃蓋板視為通過大平壁的一維導熱。

相變材料的能量方程為:

h=hs+hL

(6)

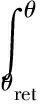
(7)

hL=fHi

(8)

f=0,θ≤θs

(9)

(10)

f=1,θ≥θL

(11)

式中h——相變材料比焓,J/kg

hs——相變材料顯熱比焓,J/kg

hL——相變材料潛熱比焓,J/kg

θ——相變材料溫度,℃

θret——相變材料初始溫度,℃

cPCM——相變材料比熱容,J/(kg·K)

f——液相率

Hi——相變潛熱,J/kg

θs——相變材料凝固溫度,℃,本文取26 ℃

θL——相變材料熔化溫度,℃,本文取28 ℃

3.2 模擬軟件

筆者采用COMSOL軟件進行模擬,建立光伏光熱墻體的三維模型。模型主要考慮輻射傳熱、固體部件內部傳熱、流體的湍流和外界環境的對流。模型將傳熱方程與流體流動的N-S方程和連續性方程進行耦合。

3.3 邊界條件與初始條件

玻璃蓋板外表面與室外空氣進行對流傳熱,玻璃蓋板外表面傳熱系數為1.0 W/(m2·K)。磚墻內壁面與室內空氣進行對流換熱,磚墻內壁面表面傳熱系數為1.5 W/(m2·K),室內環境溫度設為25 ℃。除空氣通道進出口外,光伏光熱墻體四周均為絕熱條件,空氣通道進口風速變化范圍為0.1～0.5 m/s。模型初始狀態溫度為25 ℃,進風溫度為室外溫度。室外溫度、太陽輻照度隨時間的變化見圖2[13]。圖中時段編號7表示[6:00,7:00),時段編號8表示[7:00,8:00),以此類推。模擬時間為7:00—24:00。

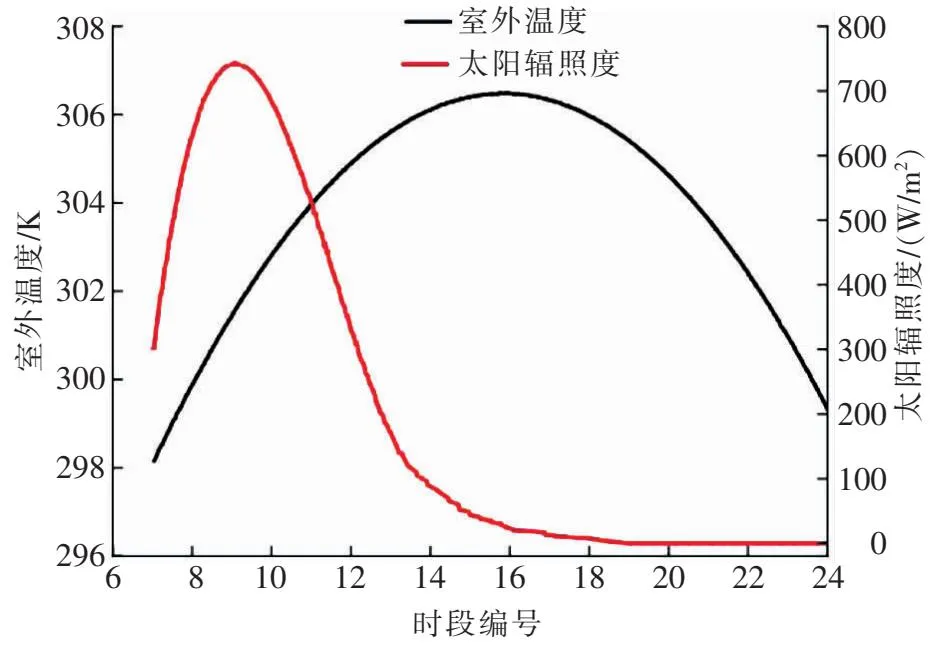
圖2 室外溫度、太陽輻照度隨時間的變化

3.4 網格無關性驗證

模型采用自由四面體進行網格劃分,在各層邊界處對網格進行加密處理。進口風速為0.1 m/s,各模型不同網格數10:30時空氣通道出口溫度見表2。由表2可知,當網格數超過51 267后,隨著網格數增加,出口溫度變化很小,說明網格數繼續增加對模擬計算結果的影響可以忽略。因此,為平衡計算時間和精度,模型網格數選取51 267。

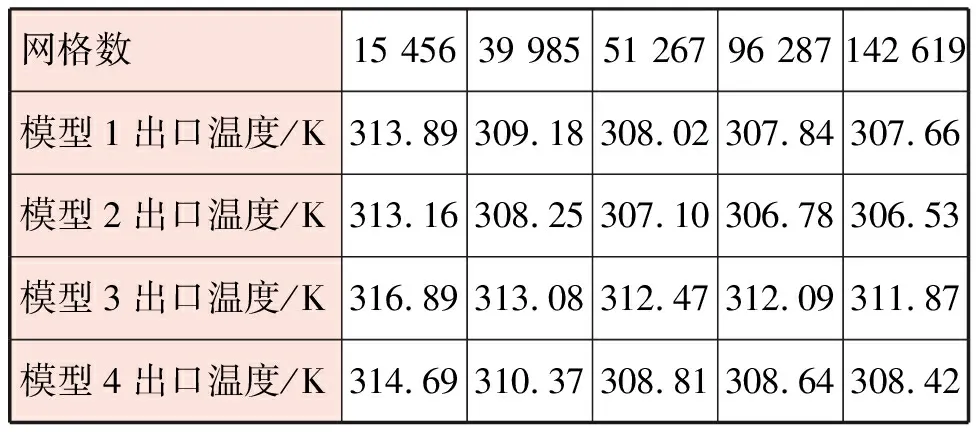
表2 各模型不同網格數10:30時空氣通道出口溫度

3.5 模型驗證

為驗證模型的準確性,建立與文獻[14]的特朗伯墻相同結構的物理模型。在進口風速為1 m/s條件下,采用本文的模型模擬出口溫度,并與文獻[14]的實驗出口溫度進行比較。室外溫度、太陽輻照度來自文獻[14]。模擬出口溫度與實驗出口溫度見圖3。由圖3可知,模擬出口溫度與實驗出口溫度變化趨勢一致。與實驗出口溫度相比,模擬出口溫度的最大相對誤差絕對值為4.29%。因此,模型的準確性比較高。

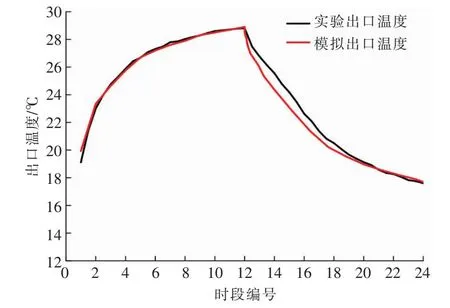
圖3 模擬出口溫度與實驗出口溫度

4 模擬結果與討論

4.1 出口溫度、空氣得熱量

① 出口溫度

進口風速為0.1、0.5 m/s時,模型1～4出口溫度分別見圖4、5。由圖4、5可知,出口溫度受室外溫度、太陽輻照度綜合影響。各模型的出口溫度均隨進口風速增大而整體下降。進口風速一定時,模型3出口溫度最高。

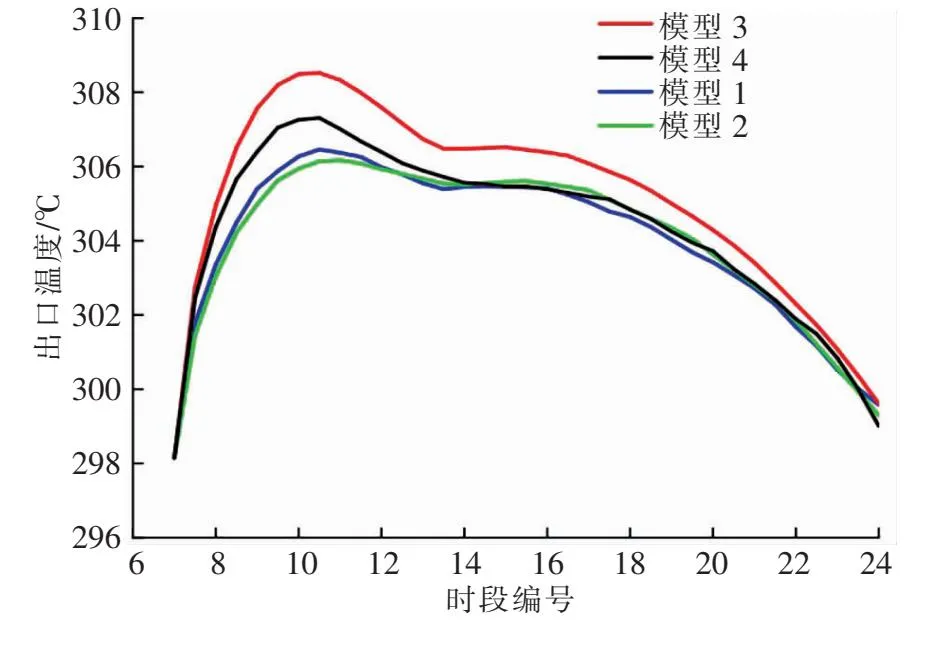
圖5 進口風速為0.5 m/s時模型1～4出口溫度

② 空氣得熱量

進口風速為0.1、0.5 m/s時,模型1～4空氣得熱量分別見圖6、7。空氣得熱量根據空氣進出口溫差、空氣質量流量計算得到。由圖6、7可知,各模型空氣得熱量變化趨勢與出口溫度變化趨勢基本一致。進口風速一定時,模型3空氣得熱量最高,模型1、2、4的空氣得熱量接近。

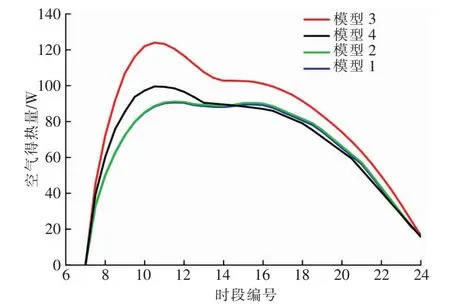
圖6 進口風速為0.1 m/s時模型1～4空氣得熱量

圖7 進口風速為0.5 m/s時模型1～4空氣得熱量

4.2 光伏板表面溫度

進口風速為0.1 m/s,10:30各模型光伏板表面(向陽面)溫度分布見圖8,圖中表面溫度的單位為K。由圖8可知,相同條件下,光伏板表面溫度由低到高的排序為模型4、模型3、模型2、模型1。這主要是由于模型4的光伏板置于空氣通道中間且相變材料層發揮了吸熱作用。

圖8 進口風速為0.1 m/s時10:30各模型光伏板表面溫度分布(軟件截圖)

由模擬結果可知,進口風速為0.1 m/s時,在有太陽輻射時段,模型4光伏板平均表面溫度在4種模型中最低,模型3僅高于模型4。

4.3 綜合性能分析

由上述分析可知,模型3能夠在較小的進口風速下得到較高的空氣出口溫度及較高的空氣得熱量。在4種模型中,模型3光伏板表面溫度低于模型1、2,僅高于模型4,有利于提高光電轉換效率。因此,模型3的綜合性能最佳。

5 結論

在較小的進口風速下,模型3能得到較高的空氣出口溫度及較高的空氣得熱量。模型3光伏板表面溫度低于模型1、2,僅高于模型4,有利于提高光電轉換效率。模型3的綜合性能最佳。