SEAD場景異構無人機配置與任務規劃聯合優化方法

王建峰,賈高偉,辛宏博,郭 正,侯中喜

(國防科技大學 空天科學學院, 湖南 長沙 410073)

無人機作為無人系統的“集大成者”,被廣泛應用于不同任務場景。大型全能型無人機平臺存在任務效費比低、系統容錯性差和升級周期長等缺陷[1-2],異構無人機系統旨在將大型平臺功能分散到空間分布的低成本單元,通過合理調度實現不同單元的動態組合和密切協作,在兼具經濟性的基礎上達到甚至超過大型平臺能力水平。

對敵防空壓制(suppression of enemy air defenses, SEAD)場景是當前異構無人機協同應用的典型場景,受到了廣泛關注[3]。當前該場景的研究多在給定無人機配置下進行,并集中于完善場景建模[3-4]與提升求解效率[5]。無人機配置是確定參與任務的無人機類型及數量[6],任務規劃是協調各單元以獲得執行方案,二者存在遞階關聯性,合理的無人機配置可以提升機間協同效率,在滿足任務需求的同時避免無人機資源浪費[6]。

SEAD場景中無人機配置和任務規劃聯合優化問題屬于異構車隊車輛路徑問題(heterogeneous fleet vehicle routing problem, HFVRP)范疇,即尋找最佳異構車隊組成和任務路線[7-8]。HFVRP是在車輛路徑問題(vehicle routing problem, VRP)的基礎上將車隊組成也作為變量,較VRP這一NP-hard問題計算復雜度更高。HFVRP包含多種擴展[9-10]——多次訪問、站點依賴、時間窗口、資源限制、非對稱路徑等,本文問題包含類似限制[3,11]:對同一目標順序執行多種任務;存在時間窗口約束和資源需求;航程和資源載荷有限,且有返航需求;任務執行要求和動力學約束使得任務路徑不對稱。這些限制極大增加了問題求解難度。

考慮無人機配置對任務執行的影響:文獻[12]針對協同搜索與攻擊場景,選擇不同數量的無人機組合進行仿真,發現增加無人機可以降低任務時間但也增加任務協調成本,數量過多反而降低整體效能;文獻[13]針對協同對地打擊場景,對比了不同機型組合及數量配置的體系貢獻率,發現高速與高隱身無人機體系貢獻率較高,無人機數量增加會提高貢獻率,但存在飽和。考慮無人機配置與任務規劃的遞階關聯性,確定合理的無人機配置:文獻[14]利用分層策略處理無人機配置與任務分配問題,對比了基于進化算法的同時求解和分層求解的效果,證明了分層策略的有效性;文獻[15]針對廣域偵察場景,利用聚類方法將目標劃分成簇,根據簇群數量確定無人機數量并進行任務指派;文獻[16]針對無人機武器配置和打擊路徑優化問題,設計了基于局部搜索策略的啟發式算法,在確定各個目標的毀傷需求的基礎上優化無人機任務路徑,驗證了啟發式算法的計算優勢。

本文針對SEAD場景特點,建立了異構無人機編隊路徑問題(heterogeneous UAV fleet vehicle routing problem, HUFVRP)模型,在任務規劃問題基礎上將各類型無人機數量也作為決策變量,充分表征目標、任務和無人機的多種約束,優化無人機使用數量與任務執行時間指標。建立了雙層聯合優化方法求解模型:上層調整無人機配置,設計了任務銜接參數引導無人機數量調整;下層求解任務規劃,改進遺傳算法能夠有效處理多種約束,并根據無人機數量變化針對性調整執行方案;雙層相互協調以獲得無人機配置和執行方案。

1 聯合優化問題建模

本節首先介紹SEAD場景想定,然后建立目標、任務和無人機模型,最后給出HUFVRP模型相關數學描述。

1.1 SEAD任務場景想定

場景目標為位置已知的雷達站,毀傷要求和時間窗口已經明確,為簡化計算做出如下想定:

1)任務場景為二維區域,不考慮地形障礙、禁飛區、突發威脅等干擾因素,目標和無人機均視為點目標。

2)目標包含多個任務,每個任務由一架無人機執行,不能忽略任務執行時間。

3)無人機存在資源和航程限制,不能無限執行任務,任務完成后需返回起飛點。

1.2 基礎模型構建

1.2.1 目標與任務模型

T={T1,…,Ti,…,TNTarget}為目標集合,數量為NTarget。MTi表示目標Ti所屬任務集合,包含偵察C、攻擊A和評估V三類任務,c∈{1,2,3}為對應類型序號。

MTi?{C,A,V}

(1)

全部任務按照目標序號排列形成任務總集合MAll={MT1,…,MTi,…,MTNTarget},任務總數量為:

(2)

1.2.2 任務耦合關系

對于某一任務,關聯矩陣中對應列的非零項為其依賴的任務,稱為前序任務,前序任務全部完成后該任務方可執行;關聯矩陣中對應行的非零項為受其影響的任務,稱為后續任務,該任務完成后后續任務方可執行。式(3)為偵察、攻擊和評估任務的關聯矩陣,第3列表示評估任務的前序任務為偵察和攻擊任務。

(3)

1.2.3 無人機模型

(4)

1.3 問題求解模型

在上述模型的基礎上,借鑒異構車隊車輛路徑問題[7,10]與無人機任務規劃[3-4]的部分研究建立HUFVRP模型。定義圖模型G(V,A),其中V={T0,T1,…,Ti,…,TNTarget}為起飛點和目標點的集合;A={(i,j)|0≤i,j≤NTarget,i≠j}為無人機目標間轉移順序的集合,(i,j)表示無人機從目標Ti轉移至目標Tj。模型相關變量如下:

該問題需要尋找合理的無人機配置方案和對應執行方案,因此針對性設置無人機數量F1和任務平均完成時間F2兩個優化目標,具體如下:

F1=NUAV

(5)

(6)

模型約束包含任務執行要求、任務時序耦合約束和無人機能力限制三類,建模如下:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

其中:式(7)約束目標包含的任務均分配給無人機執行;式(8)～(9)約束無人機從起飛點出發,執行完任務后返回出發點;式(10)約束無人機按方案順序執行任務;式(11)確保無人機在任務開始前到達目標位置;式(12)確保任務時間滿足時間窗約束;式(13)確保任務時間滿足時序耦合約束,其中Y為無窮大值;式(14)確保無人機有能力執行所分配的任務;式(15)確保無人機所執行任務的資源需求不超過其機載資源限制;式(16)確保無人機不超過航程限制;式(17)確保各類無人機使用數量不超過最大數量。

2 雙層聯合優化方法

2.1 聯合優化問題求解分析

無人機配置與任務規劃聯合優化問題包含多種類型的變量,且變量之間存在遞階關聯性,求解十分困難[14]。因此,本文設計了雙層聯合優化方法,上層進行無人機配置計算,下層進行多無人機任務規劃計算,具體見圖1。

圖1 雙層聯合優化方法結構Fig.1 Structural diagram of the two-level joint optimization method

在上層中,根據任務時間表和無人機使用率設計了任務銜接參數,精確評估各類型無人機需求,指導無人機配置方案調整。在下層中,使用改進遺傳算法在給定無人機配置下進行任務規劃計算,能結合無人機數量變化精確調整執行方案,在有限時間內能夠以更高概率獲得高質量執行方案,提升對無人機配置方案的評估準確性。

雙層聯合優化方法可以通過有限次數的迭代獲得滿足要求的無人機配置及任務執行方案,避免了無人機配置與任務規劃同時求解造成的問題空間非線性擴展,在有限的計算時間內可以獲得更高質量結果。

2.2 上層:無人機配置計算

2.2.1 任務銜接參數

(18)

(19)

(20)

(21)

本文在任務等待時間的基礎上設計了任務銜接參數指標δCI,以評估各類型無人機需求情況。某類任務的銜接參數高,說明對應的無人機數量不足,計算如下:

(22)

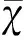
可以根據任務銜接參數的變化判斷無人機數量是否飽和:無人機增加會影響對應任務完成時間,進而影響其后續任務的最早允許開始時間。若后續任務對應無人機數量不足,參數將上升;若無人機數量充足,參數將不變,此時不需增加該類無人機。

2.2.2 無人機配置調整流程

無人機配置將在給定的初始配置方案基礎上進行調整,每次增加1架無人機,如圖2所示,具體流程如下:

圖2 無人機配置調整流程Fig.2 Flow chart of UAV configuration adjustment

步驟1：輸入初始無人機配置方案。

步驟2：調用下層任務規劃,計算當前無人機配置方案下的最優執行方案。

步驟3：根據式(18)～(22)計算任務銜接參數,根據參數對各類型無人機進行倒序排列,形成無人機增加列表。

步驟4：判斷各類型無人機是否達到其最大數量限制,若達到則從列表中刪除該類無人機。

步驟5：若上次無人機配置迭代時,任務的前序任務對應無人機增加后,該任務銜接參數沒有變化,則將對應無人機從列表中刪除。

步驟6：選擇列表中排在首位的無人機,在當前無人機配置方案的基礎上增加1架該類無人機,然后更新無人機配置方案。

步驟7：判斷是否滿足迭代終止條件,若滿足則停止迭代,否則返回步驟2進行計算。

2.3 下層:任務規劃計算

下層改進遺傳算法主要包含任務編碼與調整、任務時間表計算、局部搜索算子三部分,計算流程見圖3。

圖3 任務規劃計算流程Fig.3 Flow chart of mission planning calculation

2.3.1 任務編碼與調整

任務編碼包含目標序列、任務序列和無人機序列三部分,編碼長度與任務總數量相同,按照編碼順序從左至右計算。多層編碼情況如圖4所示,第一列表示目標T2的攻擊任務A由無人機U1執行。

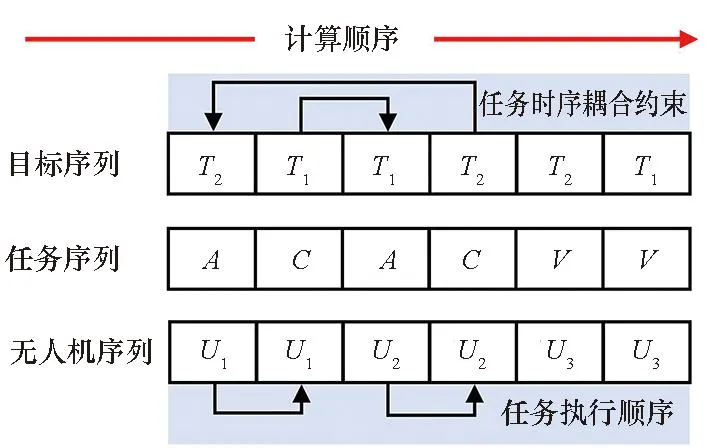
圖4 多層編碼示意圖Fig.4 Multi-layer coding schematic

由于存在時序耦合約束,若某一任務先于其前序任務執行,可能出現“死鎖”情況,導致無人機陷入無休止的等待[11]。如圖4所示,第1列和第4列分別為目標T2的攻擊和偵察任務,任務執行順序與任務時序耦合約束矛盾,導致前四個任務陷入“死鎖”。對此,本文設計了基于任務關聯矩陣的“死鎖”調整流程,具體如下:

步驟1：在原編碼基礎上生成空白的新編碼。

步驟2：根據編碼順序對原始編碼中的任務逐一進行判斷——其關聯矩陣對應列是否全部為0。

步驟3：若出現任務滿足上述條件,則立即停止判斷。將該任務從原始編碼中刪除并將其關聯矩陣對應行設為0。

步驟4：將該任務插入新編碼的當前第一空位,若編碼為空則放置于首位,無人機映射關系不變。

步驟5：判斷原始編碼是否為空,若是則輸出新編碼,否則返回步驟2。

該方法只對存在時序耦合約束的任務進行調整,其他任務的對應順序不變。

2.3.2 任務時間表計算

任務時間表將根據調整后的編碼順序進行計算,每個任務的計算過程包含無人機選擇、任務執行路徑和任務時間協調三部分。

(23)

2)任務執行路徑:采用末端航向松弛的Dubins方法[17]計算任務路徑,在滿足無人機動力學約束和任務執行需求的基礎上,將任務規劃尋優和任務路徑計算部分解耦,降低整體計算復雜度。計算過程如圖5所示,偵察無人機(A點)和攻擊無人機(B點)對目標T1和T2執行偵察和攻擊任務。藍色實線為偵察路徑:無人機需繞目標盤旋(紅色區域)搜集信息,其轉移路徑為當前位置進入盤旋航線的最短路徑,可以使用幾何切線方法計算其轉移路徑,評估任務與偵察任務計算相同。攻擊無人機路徑為紅色實線:無人機需要到達目標上方進行攻擊,目標位置將作為無人機轉移路徑的終點進行計算。

圖5 無人機任務路徑計算示意圖Fig.5 UAV path calculation schematic

3)任務時間協調:根據上述路徑可以獲得無人機到達時間,然后根據式(18)與前序任務時間和時間窗口進行協調計算任務開始時間。計算完成后需要判斷是否滿足無人機航程約束,若不滿足就選擇無人機列表中下一架無人機進行計算,若滿足則按照編碼順序計算下一項任務。

2.3.3 局部搜索算子

局部搜索算子將根據無人機配置變化對前序無人機配置下的完成時間較短的方案進行調整。主要將原方案中的部分未完成任務和等待時間較大任務添加至新增無人機執行列表,流程如下:

步驟1：選擇一個完成時間較短的任務方案,將其作為基礎方案進行調整。

步驟2：選擇新增無人機可執行的全部任務,將其中未完成任務和等待時間大于0的任務加入待調整任務列表。

步驟3：為新增無人機增加一個任務——按照待調整任務列表順序,分別將任務列表中的任務調整至基礎方案中新增無人機的執行列表末尾,形成多種新執行方案。

步驟4：計算生成的全部執行方案,選擇最優方案。

步驟5：判斷最優方案是否優于基礎方案,若占優則執行步驟6,否則執行步驟7。

步驟6：將此時最優方案作為基礎方案,并從待調整任務列表刪除最優方案中已調整的任務,返回步驟3。

步驟7：輸出此時的基礎方案。

3 場景仿真驗證

本節對無人機配置和任務規劃聯合優化方法進行仿真。分析了無人機配置過程和不同場景下的普適性;驗證了任務規劃方案的可行性與規劃方法的求解效率。

3.1 場景及參數配置

仿真場景區域范圍為150 km×150 km,起飛點為[0,0],目標隨機分布在[10,140] km×[10,140] km的區域。考慮到任務背景,目標會遠離起飛點,因此限制目標與起飛點的最小距離為60 km,目標間最小距離為20 km。目標所屬任務集合包含偵察、攻擊和評估三個任務。攻擊任務存在時間窗口,資源消耗數量為1;評估任務與攻擊任務需間隔一定時間以避免煙塵干擾。表1為無人機的性能數據[4]。任務銜接參數中等待時間調節參數為1/3,平均任務數控制系數為0.01。

表1 無人機性能數據

3.2 無人機配置方法仿真驗證

3.2.1 無人機配置過程分析

場景包含8個目標,初始無人機配置為5架無人機(1偵察、3攻擊、1評估),上層無人機配置迭代次數為10。攻擊任務時間窗前端分布在[10,30] min,后端分布在[150,180] min,評估任務與攻擊任務間隔為1 min。

為驗證本文無人機配置方法的有效性,設計了一種對比方法:在迭代時增加銜接參數最小任務所對應無人機,生成一組對比方案。結果如下:

1)無人機配置與任務銜接參數:圖6為兩種方法的無人機配置方案對比,兩種方法的無人機總數量相同,不同類型的無人機數量存在差異。圖7表示本文方法的任務銜接參數變化。如圖6和圖7所示,隨著無人機數量增加,任務銜接參數呈下降趨勢,第2次迭代時增加了偵察無人機,對應銜接參數下降,其后續的攻擊和評估任務的參數上升且變化較大,說明兩類無人機數量不足,同樣情況也在第4、6、8和9次迭代時出現,但后續任務的銜接參數波動持續減小,說明無人機數量已經較為充足。這表明無人機配置過程中觀察無人機增加對任務銜接參數的影響是有意義的。

圖6 無人機配置方案對比(左側為本文方法,右側為對比方法)Fig.6 Comparison of UAV configuration plans (left is the method in this article, right is the comparison method)

圖7 任務銜接參數變化圖Fig.7 Chart of connection impact indicator

2)無人機配置與無人機使用率:圖8為攻擊無人機使用率的變化(其余無人機均全部使用):除初始配置外,本文方法中無人機均全部使用;而對比方法在第2～4次迭代時攻擊無人機未全部使用,這是由于無人機比例不合理,偵察無人機數量過少影響偵察任務執行,使得后續攻擊任務錯過時間窗口,造成攻擊無人機資源浪費。在本文方法生成的無人機配置方案中,偵察型多于評估型,攻擊型最少。偵察型和評估型無人機性能相同,但偵察任務影響整體任務的執行,故數量較多;攻擊無人機速度最快,可以承擔更多任務,故數量較少;配置方案與無人機性能參數相符。

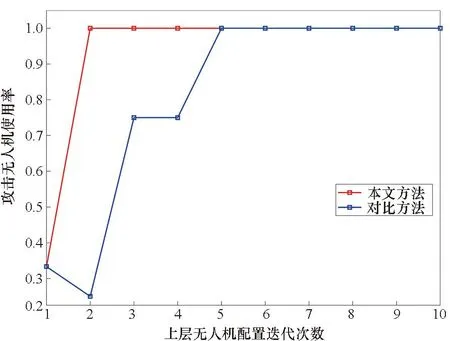
圖8 攻擊無人機使用率對比Fig.8 Comparison of attack UAV usage rates

3)無人機配置與任務平均完成時間:圖9為任務平均完成時間對比,隨無人機數量增加,任務平均完成時間持續減小,前期下降快,后期平緩,說明無人機數量增加呈現邊際效應。本文方法始終占優,第2次迭代時本文方法中任務已全部完成,但對比方法中存在未完成任務,因此差距較小;迭代后期,兩種方法調整基礎相同,增加無人機的影響降低,使得差距逐漸減小。

圖9 任務平均完成時間對比Fig.9 Comparison of average mission completion time

4)無人機配置與未完成任務:表2為未完成任務情況,圖10為未完成數量對比圖。在第1次迭代時存在部分攻擊和評估任務未完成,本文方法在第2次迭代時增加了偵察無人機,調整后任務全部完成;對比方法增加了攻擊無人機,但任務依舊未完成,說明本文方法中分類處理未完成任務的策略是有效的。

表2 未完成任務情況

圖10 未完成任務數量對比Fig.10 Comparative chart of uncompleted missions

3.2.2 多場景下無人機配置方法驗證

為驗證本文方法在不同場景的有效性,進行如下仿真:在目標和任務數量不變的情況下,隨機生成100組目標位置和對應時間窗口,在無人機總數量為7～16這十種情況下隨機生成無人機配置方案(這一范圍內變化明顯),運行本文方法和對比方法,對比任務平均完成時間變化。

圖11為不同場景下調整后與原方案時間比值的平均值,圖中數字為調整前無人機總數量。可以看出本文方法較對比方法始終占優,說明本文方法不同場景中均能夠實現對無人機配置的高效調整。在無人機數量為7～9之間時,對比方法的數據存在波動,這是由于此時無人機數量較少且配置方案隨機生成,存在部分未完成任務。隨著無人機數量增多,增加無人機的積極效果逐漸降低,這與圖9中任務平均完成時間的變化趨勢相似。

圖11 任務時間比值對比Fig.11 Comparative chart of the task time ratio

3.3 多無人機SEAD任務規劃仿真驗證

3.3.1 任務規劃方法可行性分析

選擇3.2.1節第5次迭代時生成的任務執行方案進行分析,包含9架無人機(3偵察、3攻擊、3評估)。圖12為任務執行甘特圖,圖中序號6-1中6為目標編號,1為任務類型。相同顏色的色塊為同一目標任務,粉色色塊代表任務執行時間,紅色三角表示任務時間窗口。可以看出同一目標的多個任務按順序執行,滿足時序耦合約束;任務均在時間窗口內完成,滿足時間窗約束;無人機在留空時間限制內返回出發點,滿足航程約束。

圖12 任務執行甘特圖Fig.12 Mission execution Gantt chart

3.3.2 任務規劃方法求解效率分析

為驗證本文任務規劃方法的求解效率,設置了多種算法進行對比。首先在給定無人機配置方案下分析了算法收斂性能,然后對比不同場景下的算法求解性能。相關算法參數見表3,算法種群數量為100,迭代次數為100。

表3 算法參數設置

圖13為四種算法在9架無人機(3偵察、3攻擊、3評估)時的任務平均完成時間變化,其橫坐標為任務規劃算法的迭代次數。可以看出,相較于算法1和算法2,本文算法通過增加局部搜索算子,加速了算法收斂并提升了求解質量。本文變異操作主要調整等待時間較長的任務,相較于算法3,本文算法尋優速度更快。

圖14為100組場景下的無人機配置調整和任務規劃計算:橫坐標為上層無人機配置迭代次數,縱坐標為算法最終解與初始最優解的比值,算法使用相同初始種群,比值越小解性能越好。由于第1次迭代時無前序執行方案,無法使用局部搜索算子,故不進行對比。相較于算法1和算法2,由于存在局部搜索算子,本文算法始終占優。計算后期單架無人機承擔任務數量較少,局部搜索算子可調整任務數量下降,因此算法之間差異下降。相較于對比算法3,本文算法整體占優但相差很小,與圖13中兩種算法收斂至相同解的情況相符合,為確保任務規劃的求解效果,本文使用了較大的變異概率。

圖13 算法收斂性能對比Fig.13 Comparison of the algorithms convergence

圖14 多場景下算法效果對比Fig.14 Comparison of the algorithms in multiple scenarios

4 結論

本文針對SEAD場景中無人機配置和任務規劃聯合優化問題進行研究,在任務規劃問題基礎上將各類型無人機數量也作為決策變量,充分表征目標、任務和無人機的多種約束,建立無人機編隊路徑問題模型。設計了雙層聯合優化方法,將無人機配置與任務規劃進行分層處理:上層通過分析無人機數量對任務時間的影響設計了任務銜接參數,評估各類型無人機需求并指導無人機配置調整;下層利用改進遺傳算法進行任務規劃求解,能夠滿足多類型約束獲得任務執行方案;并設計了局部搜索算子,能夠結合無人機數量變化調整執行方案以提升算法尋優效率。

仿真結果表明,無人機數量增加呈現邊際效應,合理的無人機配置能夠充分發揮各類無人機能力。本文方法能夠通過有限次數的迭代獲得滿足要求的無人機配置及任務執行方案,可以避免無人機配置與任務規劃同時求解造成的問題空間非線性擴展,在同等無人機規模下執行方案效果持續占優。該方法為SEAD場景中無人機資源配置與任務規劃提供了一套完整的解決方法,可以提高多無人機協同的指控效率。