長向量處理器高效RNN推理方法
蘇華友,陳抗抗,楊乾明
(1. 國防科技大學(xué) 計算機學(xué)院, 湖南 長沙 410073; 2. 國防科技大學(xué) 并行與分布計算全國重點實驗室, 湖南 長沙 410073)
傳統(tǒng)的卷積神經(jīng)網(wǎng)絡(luò)(convolutional neural networks,CNN)在視覺領(lǐng)域取得了巨大的成功,例如圖像分類、目標(biāo)檢測等。但是對于語言類時序數(shù)據(jù)任務(wù),某些時刻前面的輸入和后面的輸入是有關(guān)系的,CNN這種只能處理獨立輸入的模型就無法獲得較好的效果。循環(huán)神經(jīng)網(wǎng)絡(luò)(recurrent neural network, RNN)是面向時序數(shù)據(jù)處理的一類重要的深度神經(jīng)網(wǎng)絡(luò),它以序列數(shù)據(jù)為輸入,并對每一個時刻的輸入結(jié)合當(dāng)前模型的狀態(tài)給出一個輸出。目前,以RNN、長短記憶網(wǎng)絡(luò)[1](long short term memory networks, LSTM)、門控循環(huán)單元[2](gate recurrent unit, GRU)為代表的時序數(shù)據(jù)處理類循環(huán)神經(jīng)網(wǎng)絡(luò)已廣泛應(yīng)用于文件分類[3]、語音識別[4-5]和機器翻譯[6]等自然語言相關(guān)的任務(wù)處理中。隨著自然語言處理任務(wù)的復(fù)雜度增加,計算量更大的Transformer結(jié)構(gòu)和BERT模型得到廣泛的應(yīng)用,對計算資源的需求和計算效率的提升都提出很大的挑戰(zhàn)。
隨著模型規(guī)模的擴大和模型層次的增加,類循環(huán)神經(jīng)網(wǎng)絡(luò)的訓(xùn)練和推理過程對目標(biāo)平臺的執(zhí)行效率提出了極大的挑戰(zhàn)。如果沿用通用深度學(xué)習(xí)框架,諸如PyTorch[7]、TensorFlow[8]等直接按照類循環(huán)神經(jīng)網(wǎng)絡(luò)的計算過程進行碎片式、拼接化執(zhí)行,硬件的利用率得不到保障。例如,在圖形處理器(graphics processing unit, GPU)上直接調(diào)用各個算子函數(shù)進行端到端的拼接執(zhí)行,LSTM的執(zhí)行效率還不能達到峰值性能的10%。當(dāng)前有很多的工作針對RNN在GPU上的執(zhí)行過程進行了優(yōu)化,例如cuDNN[9]深度學(xué)習(xí)庫。該工作通過算子級的優(yōu)化、層級融合等多種技術(shù)手段,大大提高了RNN計算在GPU上的效率。隨著物聯(lián)網(wǎng)技術(shù)的發(fā)展,越來越多的設(shè)備接入網(wǎng)絡(luò)中,例如中央處理器(central processing unit, CPU)和數(shù)字信號處理器(digital signal processor,DSP)等,這類處理器的數(shù)量遠遠多于GPU,并且離數(shù)據(jù)源更近。然而,當(dāng)前針對CPU或者以長向量為重點計算單元的DSP的類循環(huán)神經(jīng)網(wǎng)絡(luò)計算優(yōu)化工作相對較少,只能借助于基礎(chǔ)的矩陣乘等算子進行功能實現(xiàn),以LSTM等為代表的類循環(huán)神經(jīng)網(wǎng)絡(luò)在DSP等長向量處理器上的性能優(yōu)化空間還很大,難度也很高。
首先,RNN處理對象的序列長度可變性導(dǎo)致計算不均衡。對于RNN處理的序列數(shù)據(jù)而言,不同語句的長度往往不一致,會導(dǎo)致描述語句的輸入向量長度不一致。在大batch_size主導(dǎo)的推理應(yīng)用模式下,所有的時序都會以當(dāng)前batch中序列長度最大的樣本為參照,進行樣本數(shù)據(jù)的填充以保證輸入的底層計算規(guī)模相同,從而不會影響循環(huán)的深度,同時使得分批處理執(zhí)行變得簡單,但是這種填充的方法會造成大量的額外的計算需求。其次,序列長度的可變性導(dǎo)致內(nèi)存管理的不確定性。序列長度的不同會使得內(nèi)存的分配和片上存儲分配動態(tài)變化,否則,所有序列都需要按照最長序列的需求進行存儲分配。另外,由于基于長向量處理器的智能算子庫的缺失,需要重新構(gòu)建完整的算子,需要對矩陣向量乘和矩陣乘進行優(yōu)化,同時RNN及其變種還存在大量的邊緣算子,這些算子的性能也會影響整體的效率,并且隨著參數(shù)的增大,RNN等模型中核心矩陣規(guī)模增大,矩陣計算效率的提高會放大邊緣算子計算的耗時占比。
針對上述問題,本文面向國產(chǎn)自主長向量處理器FT-M7032,研究如何高效實現(xiàn)RNN等類循環(huán)神經(jīng)網(wǎng)絡(luò)推理任務(wù)的并行優(yōu)化實現(xiàn)。首先,為了克服序列長度可變的問題,提出了一種行優(yōu)先的矩陣向量乘方法,通過改變原有的計算順序,有效地利用長向量處理器的計算單元和開發(fā)數(shù)據(jù)的局域性,最大化提高計算效率。然后,建立了一個手工匯編實現(xiàn)的高效的RNN算子庫,對矩陣向量乘算子的底層實現(xiàn)進行了深度優(yōu)化,包括單核內(nèi)的指令排布、多核任務(wù)劃分以及片上存儲空間的替換策略等。最后,高效實現(xiàn)了RNN等類循環(huán)神經(jīng)網(wǎng)絡(luò)模型的邊緣算子,并且基于有效利用片上存儲的原則對邊緣算子和矩陣向量乘算子進行了融合。通過上述工作,可以有效地利用自主長向量處理器對循環(huán)神經(jīng)網(wǎng)絡(luò)算法進行加速。
1 背景介紹
1.1 RNN介紹
1.1.1 模型結(jié)構(gòu)介紹
RNN常用于解決輸入樣本為連續(xù)序列且序列的長短不一的問題,單層RNN神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)如圖 1所示。

圖1 單層RNN神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)Fig.1 Structure of a single-layer RNN neural network
RNN每讀取一個新的輸入xt,就會生成狀態(tài)向量ht作為當(dāng)前時刻的輸出和下一時刻的輸入,將T個輸入x0~xt依次輸入RNN,相應(yīng)地會產(chǎn)生T個輸出,其中S表示神經(jīng)元。
1.1.2 計算原理
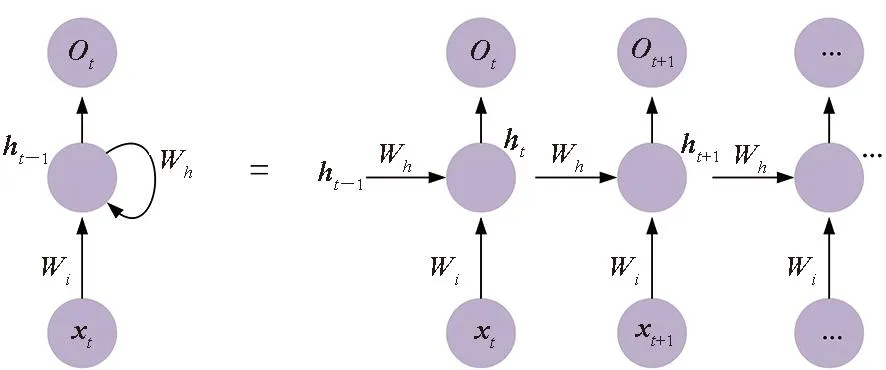
圖2 RNN神經(jīng)網(wǎng)絡(luò)的計算原理Fig.2 Calculation principle of RNN neural network
典型的RNN神經(jīng)網(wǎng)絡(luò)的計算原理如圖 2所示,主要由兩條單向流動的信息流處理組成。一條信息流從輸入單元到達隱藏單元,另一條信息流從隱藏單元到達輸出單元。假設(shè)x為輸入層,一般為向量;O為輸出層,h為隱含層,而t指計算次數(shù);Wi、Wh為權(quán)重,一般為矩陣。其中計算第t次的輸出結(jié)果如式(1)所示。
Ot=f(xt×Wi+ht-1×Wh)
(1)
從式(1)可以看出,循環(huán)神經(jīng)網(wǎng)絡(luò)的主要計算模式是矩陣向量乘,當(dāng)以batch模式執(zhí)行的時候則是矩陣乘。除此之外,還涉及tanh、sigmoid等邊緣計算過程。諸如LSTM和GRU等RNN變種模型的計算模式也主要以矩陣計算為主,區(qū)別在于LSTM相對于標(biāo)準(zhǔn)的RNN網(wǎng)絡(luò)涉及的信息流更多,即矩陣計算模塊更多。
1.2 FT-M7032長向量處理器
FT-M7032是一款國防科技大學(xué)自主研制的長向量處理器,采用異構(gòu)結(jié)構(gòu),集成了1個16核ARMv8 CPU和4個通用數(shù)字信號處理器(general purpose digital signal processor, GPDSP )。多核CPU主要負責(zé)線程管理和通信,其單精度浮點峰值性能為281.6 GFLOPS。每個GPDSP集群包括8個DSP核心,它們共享6 MB片上全局共享內(nèi)存(global shared memory, GSM)。每個計算簇中的8個DSP核和GSM通過片上網(wǎng)絡(luò)進行通信,通信帶寬可達300 Gbit/s。GSM是軟件可管理的片上存儲器,需要由開發(fā)人員維護GSM和DSP之間的數(shù)據(jù)一致性。CPU和每個GPDSP計算簇以共享內(nèi)存的方式進行數(shù)據(jù)交互。CPU可以訪問整個內(nèi)存空間,但每個GPDSP計算簇只能訪問其對于內(nèi)存通道的存儲空間,理論訪存帶寬為42.6 Gbit/s。
GPDSP中的每個DSP核心基于超長指令字(very long instruction word, VLIW)架構(gòu),包括指令調(diào)度單元(instruction fetch unit, IFU)、標(biāo)量處理單元(scale processing unit, SPU)、向量處理單元(vector processing unit, VPU)和直接內(nèi)存訪問(direct memory access, DMA)引擎,如圖3所示。IFU被設(shè)計為每個周期最多啟動11條指令,其中包含5條標(biāo)量指令和6條向量指令。SPU用于指令流控制和標(biāo)量計算,主要由標(biāo)量處理元素(scale processing element, SPE)和64 KB標(biāo)量內(nèi)存(scale memory, SM)組成,它們匹配5條標(biāo)量指令。VPU是長向量處理單位,為每個DSP核心提供主要計算性能,包括768 KB陣列存儲器(array memory, AM)和以單指令多數(shù)據(jù)(single instruction multiple datastream, SIMD)方式工作的16個矢量處理元件(vector processing element, VPE)。每個VPE有64個64位寄存器和3個融合乘加(float multiply accumulate, FMAC)單元,1個FMAC每周期可以處理2個FP32或者4個FP16的乘加計算。當(dāng)工作在1.8 GHz時,每個DSP核可以提供的單精度浮點峰值性能為345.6 GFLOPS,半精度浮點峰值性能為691.2 GFLOPS。AM可以通過2個向量load/store單元,在每個周期向寄存器傳輸512個字節(jié)。SPU和VPU之間通過廣播指令和共享寄存器傳輸數(shù)據(jù)。DMA引擎用于在不同級別的存儲器(即主存儲器、GSM和SM/AM)之間進行塊數(shù)據(jù)傳輸。

圖3 FT-M7032長向量處理器體系結(jié)構(gòu)Fig.3 FT-M7032 long-vector processor architecture
1.3 相關(guān)研究
當(dāng)前,已有一些面向循環(huán)神經(jīng)網(wǎng)絡(luò)推理的優(yōu)化研究,比如:TensorFlow使用cuDNN對底層進行優(yōu)化,但是其核心采用矩陣乘算法并不能匹配序列長度的可變性,導(dǎo)致不能最大化地利用計算資源。Holmes等提出了GRNN[10]引擎,該引擎最小化全局內(nèi)存訪問和同步開銷,并通過新的數(shù)據(jù)重組、線程映射和性能建模技術(shù)來平衡芯片上資源的使用;Zhang等[11]提出了DeepCPU,創(chuàng)建了專用緩存感知分區(qū),通過形式分析優(yōu)化共享L3緩存到私有L2緩存之間的數(shù)據(jù)移動。DeepCPU和GRNN存在類似的問題,主要優(yōu)化的是底層算子,沒有考慮序列可變帶來的問題。Gao等[12]和Silfa等[13]都試圖通過批處理相關(guān)技術(shù)進行性能優(yōu)化,但是沒有針對底層算子進行進一步的提升。除此之外,還有很多針對GPU平臺對LSTM[14]、GRU[15]和Transformer[16]的性能優(yōu)化工作,其目的都是提升在復(fù)雜模型情況下序列任務(wù)的執(zhí)行效率。
除了批處理優(yōu)化和內(nèi)核優(yōu)化,還有一些其他方式的相關(guān)工作:Kumar等[17]提出了一個名為Shiftry自動編譯器,將浮點深度學(xué)習(xí)模型編譯成8位和16位定點模型,顯著降低內(nèi)存需求,并且使用了RAM管理機制,可在物流網(wǎng)設(shè)備上獲得更低的延遲和更高的準(zhǔn)確性;Thakker等[18-21]提出了多種RNN壓縮方法,探索了一種新的壓縮RNN單元實現(xiàn),最終實現(xiàn)了比剪枝更快的推理運行時間和比矩陣分解更好的精度的效果。然而,上述工作都是在犧牲精度的情況下進行RNN推理優(yōu)化,存在一定的局限性。此外,還有一些基于現(xiàn)場可編程門陣列[22-23](field programmable gate array, FPGA)的RNN高效實現(xiàn)研究。
2 面向FT-M7032處理器的RNN推理并 行優(yōu)化
包括RNN、LSTM在內(nèi)的類循環(huán)神經(jīng)網(wǎng)絡(luò)計算過程主要分為矩陣向量乘和激活函數(shù)等邊緣算子。本節(jié)對兩類算子均進行了優(yōu)化。其中,重點對計算耗時較大的矩陣計算進行了優(yōu)化,提出并實現(xiàn)了面向長向量體系結(jié)構(gòu)的行優(yōu)先通用矩陣向量乘(general matrix vector multiplication, GEMV)算法,有效提升計算效率。為了減少對片外存儲空間的訪問,還將邊緣算子和部分矩陣算子進行了融合。
2.1 面向長向量處理器的行優(yōu)先矩陣向量方法
常見的矩陣向量乘有兩種格式,第一種為y=xA,第二種為y=Ax,RNN模型更加接近于第一種,其中x代表輸入序列向量,A代表權(quán)重矩陣。假定矩陣A的大小為k×n,向量x的大小為1×k,向量y的大小為1×n,且
(2)
式中,j=0,1,2,…,n-1。傳統(tǒng)的實現(xiàn)方式是取向量x中的第i個元素與矩陣A的每一行的第i個元素進行對應(yīng)的計算。然而,對于超長向量體系結(jié)構(gòu)來說,這種實現(xiàn)方式難以有效利用長向量處理單元:一是矩陣A需要轉(zhuǎn)置,增加大量的數(shù)據(jù)訪問,對于存儲帶寬本就較低的處理器而言,會導(dǎo)致性能急劇下降;二是需要對最后結(jié)果進行規(guī)約,FT-M7032處理器結(jié)構(gòu)對于規(guī)約計算并不友好。
針對這一問題,提出按行計算的GEMV算法,該向量化方法的基本思想是每次計算矩陣A的一行元素,計算向量y的第j個值由k次向量累加完成。首先將向量x分成p組,假定k能被p整除,每組包含q個元素,然后取矩陣A的q行,與向量x對應(yīng)的q個元素進行乘加運算,之后分別從矩陣A以及向量x取下一組元素進行對應(yīng)的計算,并且與上一組的結(jié)果進行相加,最后在p組內(nèi)部進行對應(yīng)相加運算。圖 4表示其中組內(nèi)的矩陣向量乘實現(xiàn)。
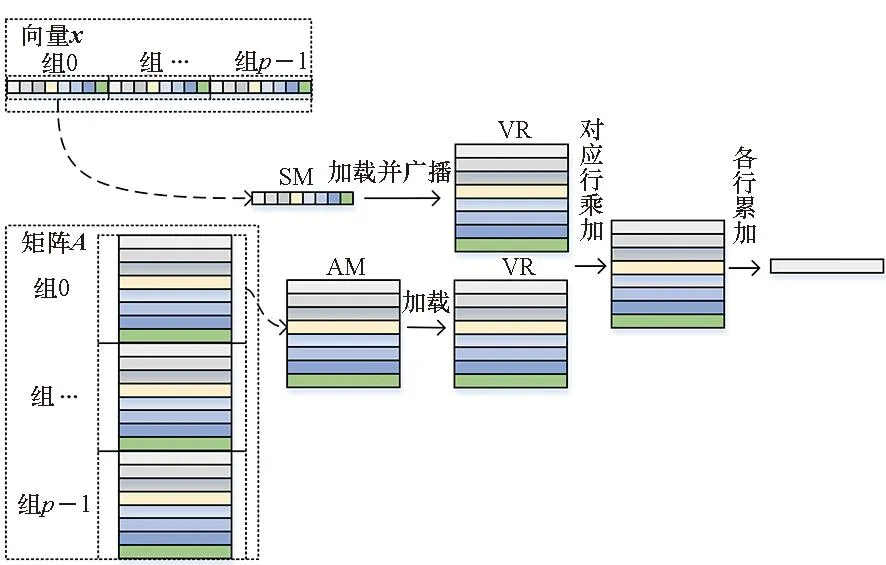
圖4 組內(nèi)的矩陣向量乘實現(xiàn)Fig.4 Matrix vector multiplication implementation within a group
基于上述原理,為減少循環(huán)開銷,本文通過手動編排匯編代碼,讓VPE的v個FMAC指令同時并行執(zhí)行,并根據(jù)FMAC指令延遲槽進行循環(huán)展開,以獲得較好的流水排布和最佳的性能。以q=8為例,核心匯編循環(huán)如圖 5所示。SLDH指令表示將輸入數(shù)據(jù)從SM中按照半字大小格式加載到標(biāo)量寄存器中,這時標(biāo)量寄存器中低位數(shù)據(jù)為傳輸?shù)陌胱执笮〉臄?shù)據(jù),高位數(shù)據(jù)為0,但是因為標(biāo)量寄存器可以存儲單字大小的數(shù)據(jù),所以使用SFEXTS32L指令將標(biāo)量寄存器中的低位數(shù)據(jù)擴展到高位上,使得高低位的數(shù)據(jù)都為傳輸進來的單字大小的數(shù)據(jù),繼而使用SVBCAST指令將數(shù)據(jù)從標(biāo)量寄存器廣播到向量寄存器VR,使用VLDW/VLDDW指令將數(shù)據(jù)以單字/雙字大小從AM加載到另外的向量寄存器VR,并使用VFMULAS32指令對不同的VR寄存器中的數(shù)據(jù)進行乘加計算,其中的SBR指令為條件跳轉(zhuǎn)語句,用于算法的循環(huán),SUB指令用于控制循環(huán)變量的自減。

圖5 矩陣向量乘的核心循環(huán)Fig.5 Core loop of GEMV
本文提出的矩陣向量乘的匯編代碼的計算單元利用率很高,當(dāng)k=1 024時,最高利用率為99.3%;當(dāng)k=512時,最高利用率為98.6%;當(dāng)k=256時,最高利用率為97.3%。
2.2 向量拼接
如式(3)所示,循環(huán)神經(jīng)網(wǎng)絡(luò)計算包括大量的矩陣向量乘。
x×Wi+Bi+h×Wh+Bh
(3)
式中,x和h為向量,Wi和Wh為權(quán)重,Bi和Bh為偏置。如果按照式(3)進行計算和長向量內(nèi)核調(diào)用,需要調(diào)用2次矩陣向量乘,且每次調(diào)用的計算量較小,對于計算能力較強的處理器,會導(dǎo)致硬件利用率較低。此外,對于計算單元足夠多的處理器,這種直接碎片式的調(diào)用也導(dǎo)致大量碎片式存儲空間的搬運過程。如式(3)所示,完成RNN的一次操作,需要11次數(shù)據(jù)傳輸(每個原始數(shù)據(jù)需要1次,一共6次;每次運算出的中間結(jié)果需要一次輸出數(shù)據(jù)的傳輸,一共5次)。基于上述問題,可以通過數(shù)據(jù)拼接,將多個小規(guī)模計算拼接成較大規(guī)模數(shù)據(jù)的計算,以利用長向量處理單元的強大計算能力和DMA的大塊數(shù)據(jù)傳輸效率。
具體而言,將x和h以及Wi和Wh分別進行拼接,并將Bi和Bh進行累加,將式(3)轉(zhuǎn)換成:
x×Wi+Bi+h×Wh+Bh=x_h×Wih+Bih
(4)
按照上述公式,1次RNN樣本的運算只需要進行1次加法以及1次乘法,以及5次數(shù)據(jù)傳輸(每個原始數(shù)據(jù)需要1次,共3次;每次運算出的中間結(jié)果需要一次輸出數(shù)據(jù)的傳輸,共2次)。這樣做的好處在于,雖然整體的計算量不變,但是通過減少碎片化數(shù)據(jù)的傳輸,提高了帶寬利用率。合并方式如圖6所示。對于有多個時間步的計算,輸入x_hitj按照如圖 6方式在雙倍速率同步動態(tài)隨機存儲(double data rate synchronous dynamic random access memory, DDR)中排列。其中x_hitj表示第i個batch的第j個時間步輸入數(shù)據(jù)。
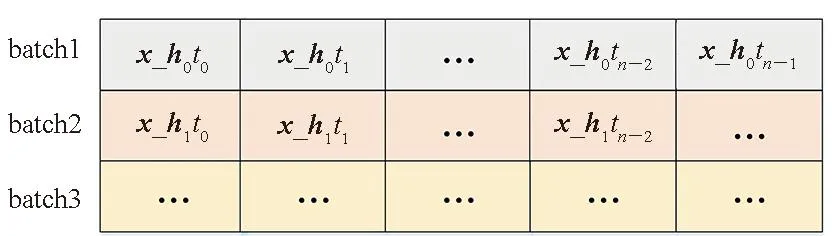
圖6 向量拼接后輸入數(shù)據(jù)結(jié)構(gòu)Fig.6 Input data structure after vector concatenation
2.3 邊緣算子融合
RNN模型的邊緣算子一般為tanh和sigmoid,公式分別如式(5)和式(6)所示。
(5)
(6)
這兩個算子都和ex相關(guān),所以問題轉(zhuǎn)換為高效求解ex。本文通過泰勒展開的方式構(gòu)造ex的近似值,如式(7)所示。
(7)
為了更快收斂,采用以下步驟進行優(yōu)化(需要注意的是,該方法需要上下界約束):
步驟1:預(yù)先計算ln2。
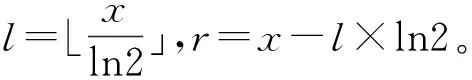
步驟3:ex=er+l×ln2=erel×ln2=er·2l。
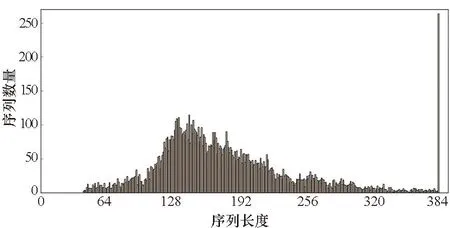
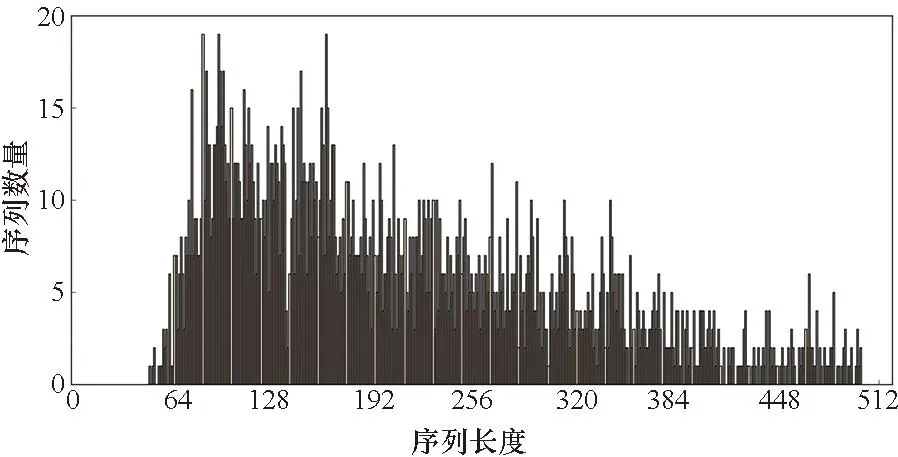
因為0≤r 算法1 基于DSP的ex匯編核心算法 當(dāng)使用訓(xùn)練框架時,如TensorFlow或PyTorch來推理RNN模型時,大量的函數(shù)調(diào)用和中間臨時結(jié)果傳輸導(dǎo)致大量的時間花費在一些非計算密集型的邊緣算子上。可通過內(nèi)核融合的方法減少內(nèi)存訪問的數(shù)量,利用片上存儲提高數(shù)據(jù)的局域性。同時也可以減少內(nèi)核啟動開銷以減少額外開銷。本文主要實現(xiàn)了兩個級別的內(nèi)核融合策略:對于tanh、sigmoid等逐元素計算的算子,利用寄存器進行計算單元的融合;而對于向量加、點乘等需要兩個輸入的算子,利用核內(nèi)空間AM的大容量進行算子融合。 FT-M7032處理器采用共享GSM和DDR的存儲結(jié)構(gòu),且擁有最多8個計算核心。如何利用更多的計算核心對批量數(shù)據(jù)進行處理以提高計算效率,以及如何進行任務(wù)劃分以提高片上存儲利用率成為多核優(yōu)化的關(guān)鍵所在。 FT-M7032異構(gòu)處理器通過DMA完成核內(nèi)外空間的數(shù)據(jù)傳輸,例如從DDR到GSM或者AM等片上存儲空間,常用的傳輸方式包括點對點和廣播兩種方式。 通常來說,GSM的帶寬是DDR帶寬的10倍以上,為了更好地提高存儲帶寬利用率,可將數(shù)據(jù)盡可能地存放在GSM上,但是由于GSM的空間有限,所以有些數(shù)據(jù)也會溢出到DDR中。為了盡可能地減少對DDR的訪問,本文設(shè)計了數(shù)據(jù)敏感的數(shù)據(jù)劃分方式,根據(jù)輸入數(shù)據(jù)的大小采用不同的數(shù)據(jù)存儲模式和傳輸方式。 當(dāng)向量長度較大時,即n較大的情況下,在n方向分核。將Wih和Bih存儲在DDR上,通過點對點傳輸?shù)胶藘?nèi)空間AM;x存儲在GSM中,通過點對點傳輸?shù)胶藘?nèi)空間SM;O存儲在AM中,通過點對點傳輸?shù)紻DR中,如圖 7所示,圖中nc表示計算核的數(shù)量。此外,還根據(jù)權(quán)重的大小對數(shù)據(jù)存儲生命周期進行了優(yōu)化,如果滿足式(8),將會讓W(xué)ih常駐在AM中,極大地減少數(shù)據(jù)在AM和DDR之間的傳輸。 n-nc×z<0 (8) 式中,z表示FMAC能處理的向量長度。 在這種實現(xiàn)模式下,每個核上的x是一樣的,而每個核上的Wih和Bih是不一樣的。因為在GSM上使用點對點和廣播方式的傳輸效率近似,所以采用點對點傳輸。 然而,當(dāng)n較小時,根據(jù)向量長度在n方向分核會導(dǎo)致部分核長時間無法利用。而推理應(yīng)用通常會采用高吞吐模式,將大批量數(shù)據(jù)捆綁輸入,也就是說有很多條序列同時輸入,使得batch_size(bsz)很大。針對這種情況,本文設(shè)計了序列維度的任務(wù)劃分方式,如圖8所示。 當(dāng)輸入序列數(shù)量較多時,采用bsz方向并行的模式。將Wih和Bih放在DDR上,通過廣播方式傳輸;x放在GSM上,通過點對點傳輸。 在這種實現(xiàn)方式中,每個核上的x不一樣,而Wih和Bih是一樣的。考慮到在DDR上使用點對點和廣播方式的傳輸效率差異大,而廣播方式效率更高,因此采用廣播傳輸。 圖7 基于向量長度并行的多核分配方案Fig.7 Multi-core distribution scheme based on vector length parallelism 注:Wihnp表示W(wǎng)ih的列數(shù)除以nc并且向上取整。 對提出的面向長向量處理器的RNN并行優(yōu)化實現(xiàn)在自主FT-M7032處理器上進行了測試,并與基于FT-2000+(16核)以及Intel Gold 6242R(20核)的實現(xiàn)結(jié)果進行了對比和分析。首先,基于SQuAD-1.1[24]以及OpenSLR LibriSpeech Corpus[25]兩個數(shù)據(jù)集,分別在FT-M7032處理器和其他平臺上對RNN和LSTM模型進行了性能測試以及比較;然后,對提出的各種優(yōu)化方法的效果進行了細化評估;接著對循環(huán)神經(jīng)網(wǎng)絡(luò)中主要的計算模式矩陣向量乘進行了測試;最后與傳統(tǒng)方法進行了對比。 測試中向量x的大小為1×k,矩陣A的大小為k×n,得到的向量y的大小為中1×n。為了測試的多樣性,對RNN以及LSTM模型常用的4個參數(shù)進行了6組配置,如表1所示。其中batch_size(bsz)、input_size(ipts)、hidden_size(hids)、num_layers(nl)分別代表批次大小、輸入大小、隱藏層大小、網(wǎng)絡(luò)層數(shù)。 表1 RNN測試參數(shù) 采用矩陣向量乘的方法適應(yīng)序列的可變性,并將邊緣算子與矩陣乘算子進行了融合以獲得在長向量處理器上的良好性能。以上述兩個數(shù)據(jù)集為輸入,分別在FT-M7032、FT-2000+(16核)以及Intel Gold 6242R(20核)上對RNN和LSTM的性能進行了測試,對同一數(shù)據(jù)集在不同平臺下的吞吐量進行了對比。其中后面兩個CPU平臺的實現(xiàn)是基于PyTorch框架,后端是標(biāo)準(zhǔn)的深度神經(jīng)網(wǎng)絡(luò)庫。測試結(jié)果分別如圖9和圖10所示。 從圖9中可以看出,在各組參數(shù)下,提出的方法在兩個數(shù)據(jù)集上的性能都能大幅超過對應(yīng)循環(huán)神經(jīng)網(wǎng)絡(luò)模型在FT-2000+上的性能。從多組參數(shù)配置的加速效果可以看出,當(dāng)參數(shù)配置較大時,加速效果更加明顯,主要是因為:參數(shù)小時的計算量也較小,可并行度較低,計算占比較低;而當(dāng)參數(shù)量增大時,可并行度增加,計算占比增加,加速比有明顯提升,最大可高達62.68。 圖9 基于長向量處理器的RNN和LSTM模型推理相比于FT-2000+的性能加速比Fig.9 Performance acceleration ratio of RNN and LSTM model inference based on long vector processor compared to FT-2000+ 從圖10中可以看出,除了小參數(shù)的情況,提出的方法在兩個數(shù)據(jù)集上的性能都能超過對應(yīng)模型在Intel CPU上的性能,RNN模型加速比最大能達到3.51,LSTM模型最大加速比為3.12。而FT-M7032的峰值計算能力與Intel CPU相當(dāng),說明提出的實現(xiàn)方法針對硬件結(jié)構(gòu)進行了有效的優(yōu)化。 圖10 基于長向量處理器的RNN和LSTM模型推理相比于Intel Gold 6242R的性能加速比Fig.10 Performance acceleration ratio of RNN and LSTM model inference based on long vector processor compared to Intel Gold 6242R 本文采取矩陣向量乘的方法而不是矩陣乘的方法進行RNN及其變種LSTM的處理,主要原因是batch中的序列長度不一致導(dǎo)致計算量不一致,如果使用矩陣乘實現(xiàn),將引入很多的無效計算。分析了兩個數(shù)據(jù)集的序列長度分布,如圖11、圖12所示。從圖中可以看出,序列長度非常不均勻,如果對序列長度進行補齊的話,將存在大量的無效計算,可能導(dǎo)致性能的下降。 圖11 SQuAD-1.1數(shù)據(jù)集序列長度分布Fig.11 Sequence length distribution of SQuAD-1.1 dataset 圖12 OpenSLR LibriSpeech Corpus數(shù)據(jù)集序列長度分布Fig.12 Sequence length distribution of OpenSLR LibriSpeech Corpus dataset 在不同的參數(shù)下,為了適應(yīng)可變序列,采用矩陣向量乘的方法,并且根據(jù)數(shù)據(jù)集的特點,將SQuAD-1.1的最大序列長度設(shè)置為384,將OpenSLR LibriSpeech Corpus數(shù)據(jù)集的最大序列長度設(shè)置為500,將適應(yīng)可變序列的方法與固定最大序列長度的方法進行對比,其中RNN模型的對比結(jié)果如圖13所示。 圖13 使用RNN模型時,可變序列長度相比于固定序列長度的性能加速比Fig.13 Performance acceleration ratio of variable sequence length compared to fixed sequence length when using RNN model 從圖13中可以看出,當(dāng)bsz、ipts以及hids較小時,提出的實現(xiàn)方式收益較小,因為在此情況下,主要的時間消耗在數(shù)據(jù)搬運上,提高計算效率的影響不大。但是隨著各個參數(shù)的增大,數(shù)據(jù)搬運的耗時占比慢慢減小,因此,通過針對算子等進行的極致優(yōu)化效果變得明顯,最高能產(chǎn)生1.79的加速比。 本文實現(xiàn)了高效的矩陣向量乘算子庫,通過手動編排匯編的方式提高計算效率,對優(yōu)化實現(xiàn)后的矩陣向量乘和基于PyTorch框架下矩陣向量乘在FT-2000+CPU的執(zhí)行時間進行對比,不同規(guī)模下的加速比如圖14所示。 從圖14中可以看出,所有參數(shù)下,提出的矩陣向量乘的效率都高于FT-2000+,而當(dāng)矩陣向量維度比較大的時候,性能提升更加明顯,性能提升可達6倍以上。同時,本文注意到矩陣向量乘的加速效果不如RNN以及LSTM模型整體效果明顯,其原因有兩點:第一點是矩陣向量乘本質(zhì)上不受可變序列長度的影響;第二點是使用RNN以及LSTM模型時,可以采用大批次,能更好地復(fù)用權(quán)重。 圖14 基于長向量處理器的矩陣向量乘相比于 FT-2000+的性能加速比Fig.14 Performance acceleration ratio of matrix vector multiplication based on long vector processor compared to FT-2000+ 通用的框架,如PyTorch,使用矩陣乘實現(xiàn)RNN模型的推理,其主要考慮的問題是可以批量執(zhí)行。因此,矩陣乘算法需要首先對序列進行預(yù)處理,將所有的帶處理的序列進行對齊,然后進行并行處理。這種模式需要更大的內(nèi)存空間,同時會引入很多額外的計算。本文對比了在長向量處理器上使用矩陣乘以及矩陣向量乘對RNN模型進行推理的吞吐量性能,如圖 15所示,提出的基于矩陣向量乘的方法在RNN模型推理上的加速比最大可達1.82。 圖15 基于矩陣向量乘優(yōu)化方法相對于矩陣乘實現(xiàn)方法的RNN模型推理加速Fig.15 Performance acceleration ratio of matrix-vector multiplication for RNN model inference compared to matrix multiplication 本文面向FT-M7032長向量處理器對RNN模型推理進行了優(yōu)化。首先,對RNN神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)進行剖析,將其分為了矩陣向量乘算子和邊緣算子,并根據(jù)處理器的體系結(jié)構(gòu),針對矩陣向量乘算子,提出了基于按行計算的矩陣向量乘算法,在多核層面采用了內(nèi)核選擇等優(yōu)化方法;而針對邊緣算子,提出了兩個級別的內(nèi)核融合優(yōu)化方法,并且使用手寫匯編對單核的兩種算子進行了優(yōu)化,旨在挖掘FT-M7032處理器的最佳性能。實驗表明,提出的面向長向量處理器的RNN實現(xiàn)效果較好,相較于FT-2000+以及Intel Gold 6242R,LSTM模型最多分別獲得了62.68倍以及3.12倍的性能加速。
2.4 數(shù)據(jù)敏感的多核并行優(yōu)化方法


3 實驗結(jié)果和分析
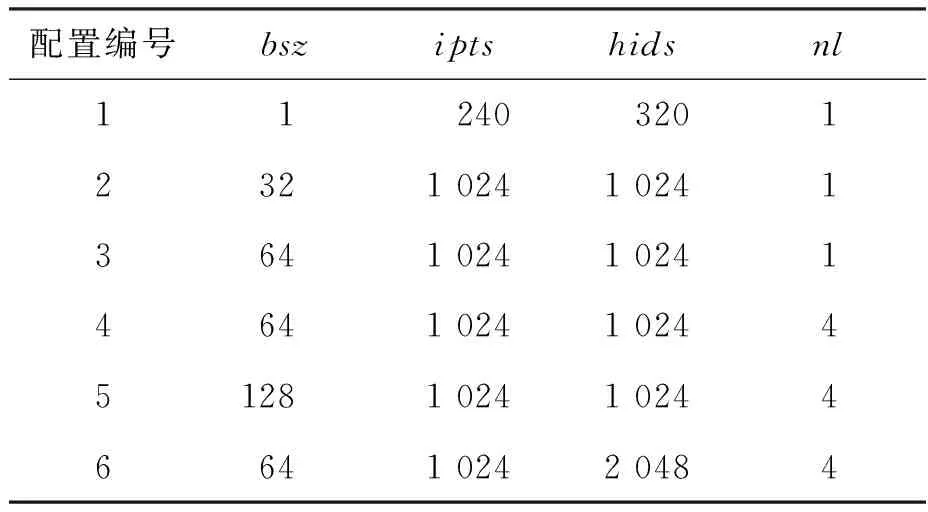
3.1 整體性能評測

3.2 基于可變序列的RNN以及LSTM性能加速效果
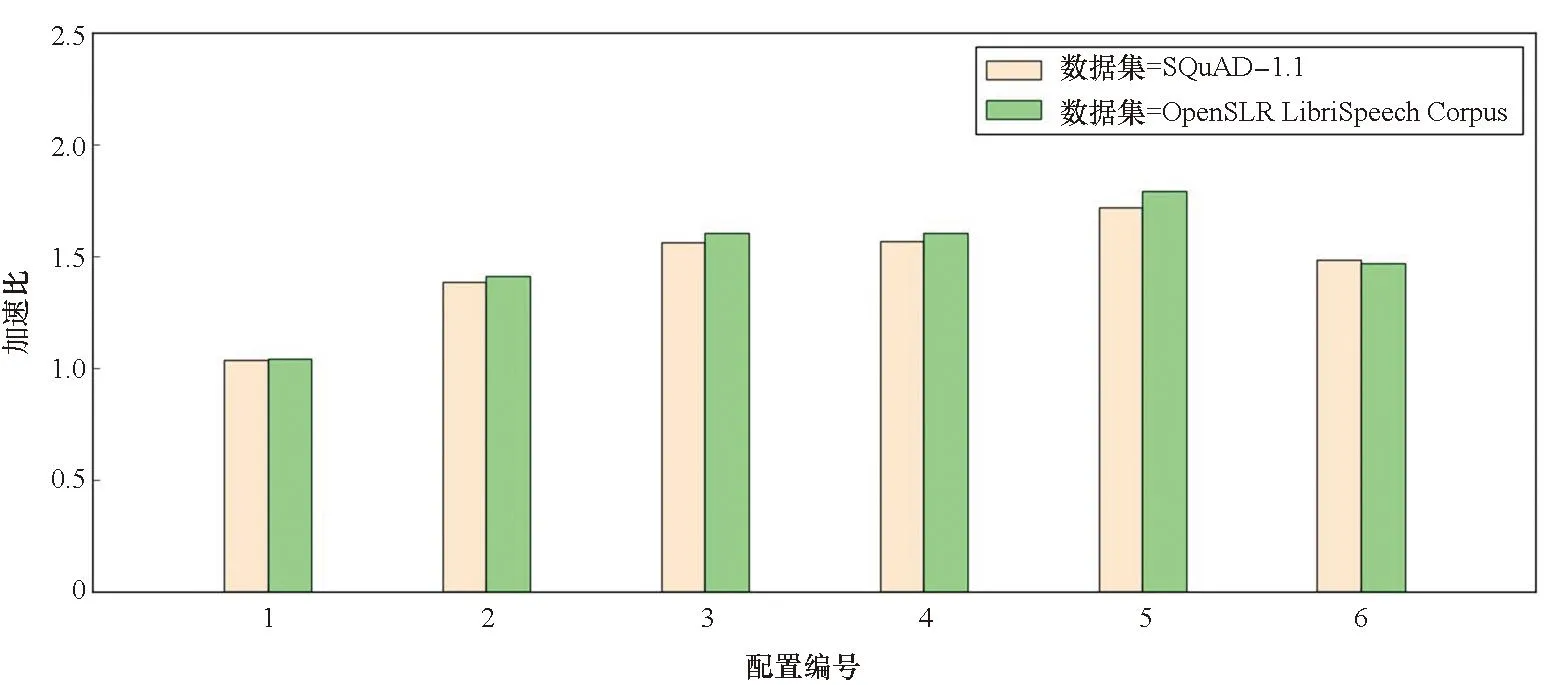
3.3 矩陣向量乘性能

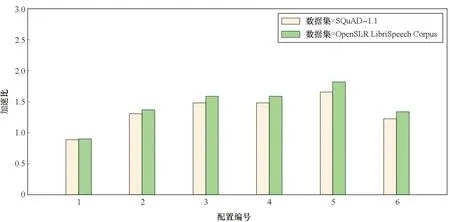
3.4 不同RNN推理方法對比測試
4 結(jié)論

