球形破片侵徹明膠運動模型及破片參數敏感性分析
蔣明飛,陳 莉,劉 坤,趙 磊,吳志林
(南京理工大學 機械工程學院, 江蘇 南京 210094)
破片是輕武器彈藥中常見的殺傷元,可按需預制成球形、菱形、小箭形等形狀,并裝入套筒式彈體中,通過炸藥或發射藥獲得必要的初始速度以殺傷目標[1]。彈道明膠因與人體肌肉組織相似的密度、黏彈性及良好的均勻性、透明性,在生物醫學和創傷彈道中被廣泛用作軟組織模擬物[2-4]。
眾多學者開展了破片與明膠靶標的實驗與仿真研究[5-15]。劉飛等[5]在實驗研究的基礎上,結合瞬態動力分析軟件,對球形殺傷元在明膠介質中的運動規律進行了分析研究,并提出了明膠靶標的標定方法。溫垚珂等[6]分別使用Lagrange法、任意拉格朗日-歐拉(arbitrary Lagrange-Euler, ALE)法和SPH-Lagrange耦合算法對鋼球高速侵徹明膠的動力學過程進行了模擬,發現Lagrange法的計算精度和效率最高;并在此基礎上使用Lagrange法模擬了三種球形破片中等速度侵徹明膠的作用過程[7]。文獻[8-9]利用LS-DYNA軟件模擬了球形破片與明膠的相互作用過程,研究了速度衰減、能量變化和空腔演化規律。李金明等[10]對4.8 mm球形破片侵徹明膠靶標的過程進行了數值仿真研究,發現破片質量是影響明膠靶標瞬時空腔最大直徑及侵徹深度的主要因素。苑大威等[11]采用仿真方法研究了菱形破片以不同速度、姿態角侵徹明膠的作用過程,總結菱形破片翻轉規律,得出菱形破片侵徹明膠深度的經驗公式。Swain等[12]、Ye等[13]開展了不同直徑的鋼球以不同速度侵徹明膠的實驗,建立了侵徹深度的經驗公式。張志倩等[14]通過實驗和數值模擬方法研究了低速陶瓷球侵徹明膠的過程,發現陶瓷球直徑是影響侵徹深度的主要因素。田浩成等[15]利用遺傳算法對不同工況的仿真數據進行擬合,得到了計算瞬時空腔的簡化數學模型。
由于數值模擬方法計算效率較低,很多學者通過理論建模的方法分析了球形破片侵徹明膠的運動規律。Seglets[16]認為球形破片侵徹明膠時會受到慣性阻力和材料阻力的作用,其中材料阻力是應變率的指數函數,并建立了球形破片侵徹明膠的運動模型。Liu等[17]考慮球形破片分離角和速度的關系,建立了球形破片慣性阻力系數和最大瞬時空腔的聯系;后又基于準靜態柱形空腔膨脹理論,提出了包含慣性項和率相關強度項的球形破片侵徹明膠的阻力模型[18]。莫根林等[19-21]建立了長方體破片侵徹明膠的六自由度運動模型,并根據實驗數據試算得到長方體破片運動模型中的動態阻力系數;利用球形破片在明膠中的運動模型和空腔實驗數據,建立了空腔振幅、角頻率與能量的經驗公式。劉坤等[22-24]在考慮了慣性阻力和黏性阻力的模型基礎上引入明膠靜態強度項;后又提出了考慮明膠應變率效應的理論模型,使用最小二乘法確定了最佳慣性阻力系數和黏性阻力系數。以上這些理論模型均建立在破片已經完全進入明膠中的假設,忽略了球形破片由空氣進入明膠這個跨介質的階段。
本文基于動態空腔膨脹理論,考慮了球形破片由空氣進入明膠這個階段的速度衰減,建立了球形破片侵徹明膠的分段運動理論模型,通過實驗確定了最優阻力系數。利用該模型分析了理論計算過程中的誤差來源;并通過理論推導和Sobol′法去分析球形破片參數對侵徹深度影響的敏感性。
1 理論模型
根據動態空腔膨脹理論,假設侵徹靶材的彈頭表面微元的受力由材料阻力和慣性阻力組成,其中材料阻力與靶材的屈服強度相關,慣性阻力與靶材密度和法向膨脹速度平方的乘積相關[25]。借鑒上述分析方法,假設球形破片為剛性球體,侵徹明膠時迎風面上各微元面僅受垂直于微元面的慣性阻力和材料阻力的作用,則微元所受阻力f可表示為:
f=[AY+Bρt·(v·n)2]·n·dS
(1)
式中,Y和ρt分別是明膠材料的屈服強度和密度,A和B分別是無量綱材料阻力系數、慣性阻力系數,v為微元的速度,dS為微元的面積,n為微元的外法線方向。
為描述球形破片在明膠中的運動規律,建立固定坐標系O′x′y′z′,使得O′y′z′平面和明膠入射平面重合。在球形破片的質心建立局部坐標系Oxyz,使得x軸和x′軸平行、y軸和y′軸平行。坐標系與明膠的相對位置如圖1所示。
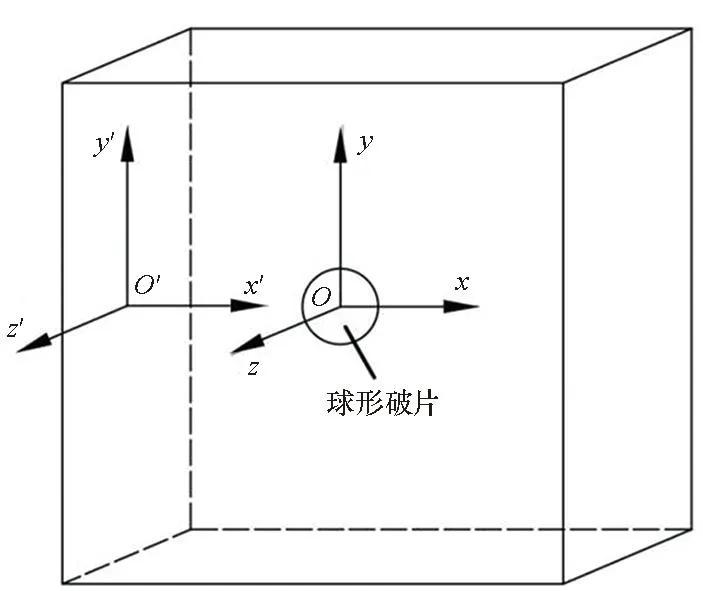
圖1 模型坐標系Fig.1 Coordinate system of the model
僅考慮球形破片在x′方向的平動,不考慮球形破片的空間轉動和在其他方向的平動,則球形破片表面微元的速度和質心的速度相同均為v。在局部坐標系Oxyz中,令微元面的直角坐標為(x,y,z)、柱坐標為(r,θ,x),兩者的關系可表示為:
(2)
由于微元處于球形破片的表面,其位置坐標滿足球面幾何條件:
x2+y2+z2=R2
(3)
式中,R為球形破片半徑。將式(2)代入式(3)可得:
x2+r2=R2
(4)
對式(3)等號兩側進行微分運算,可得微元的單位外法線n為:
(5)
將式(2)和式(4)代入式(5),得到單位外法線n的柱坐標形式為:
(6)
柱坐標下微元的面積大小dS可表示為:
dS=R·dθ·dx
(7)
若微元處在明膠內,在固定坐標系中,需滿足以下關系:
x′=xc+x>0
(8)
式中,x′、xc分別為微元和球形破片質心在固定坐標系O′x′y′z′中的坐標。整理式(8)可得:
x>-xc
(9)
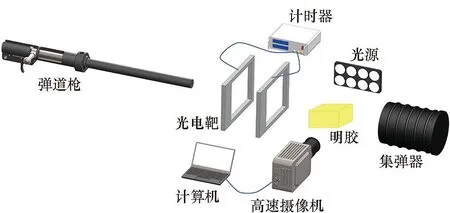
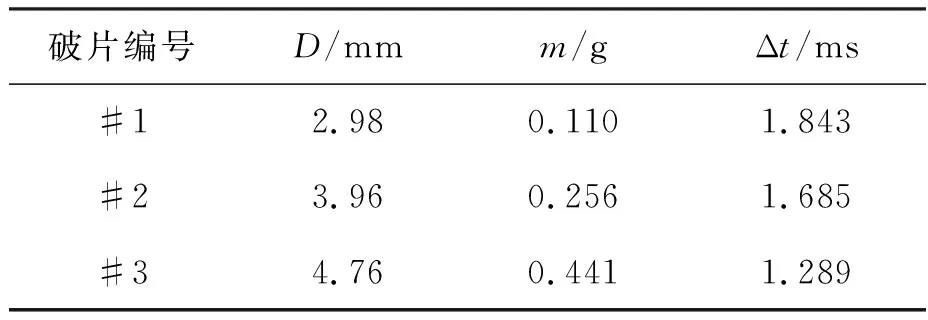
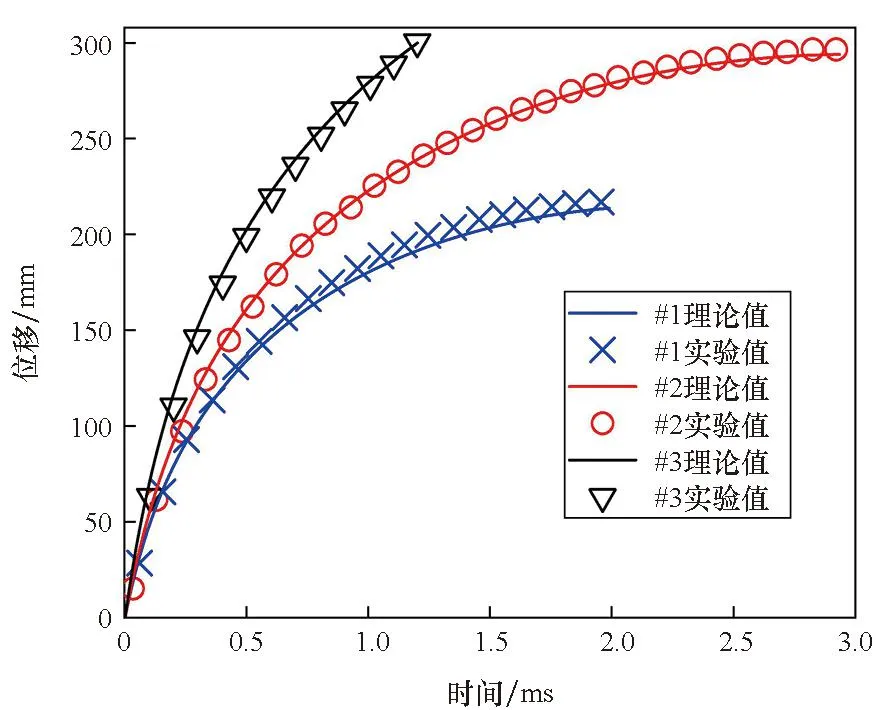
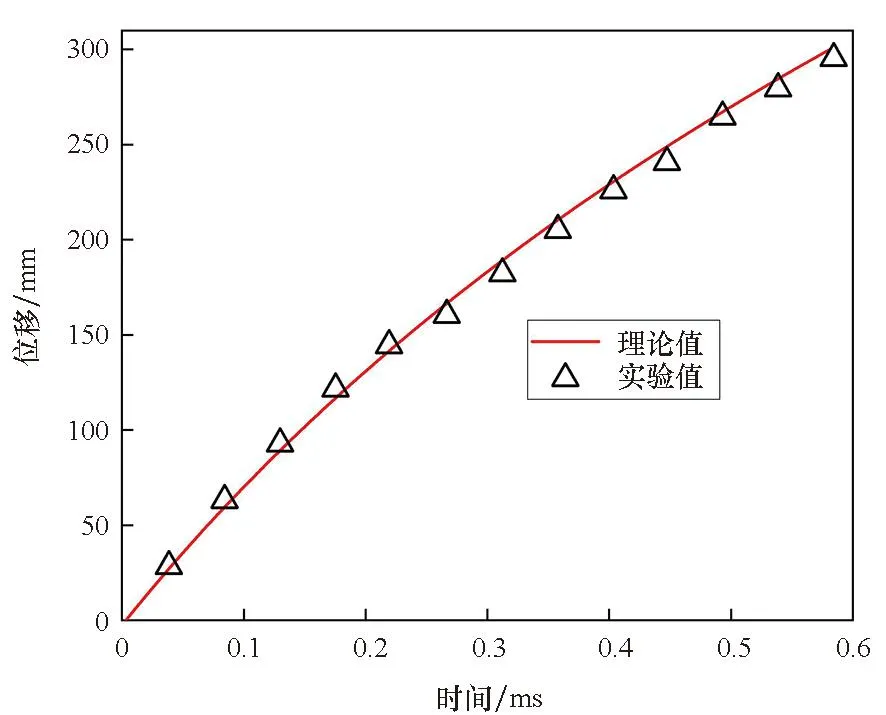
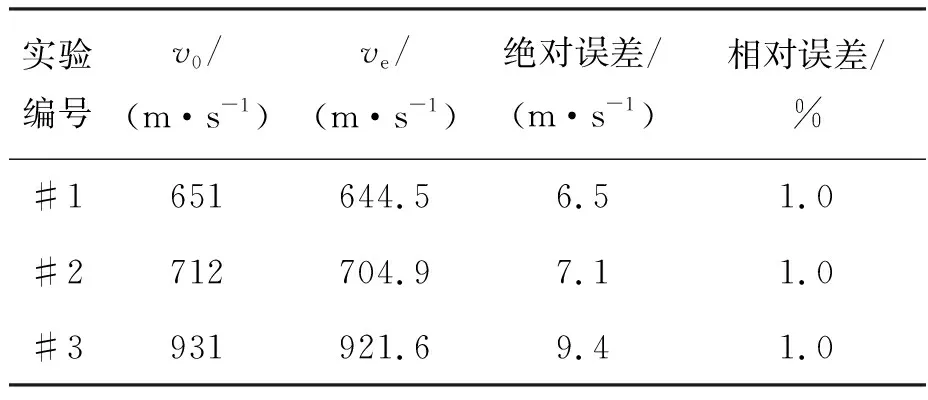
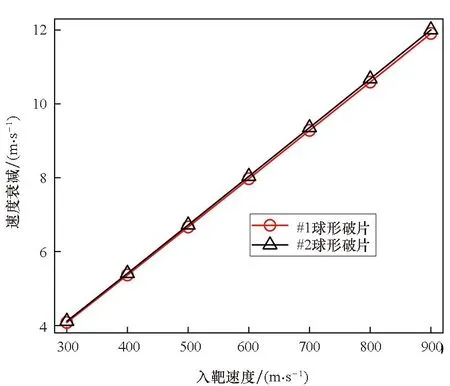
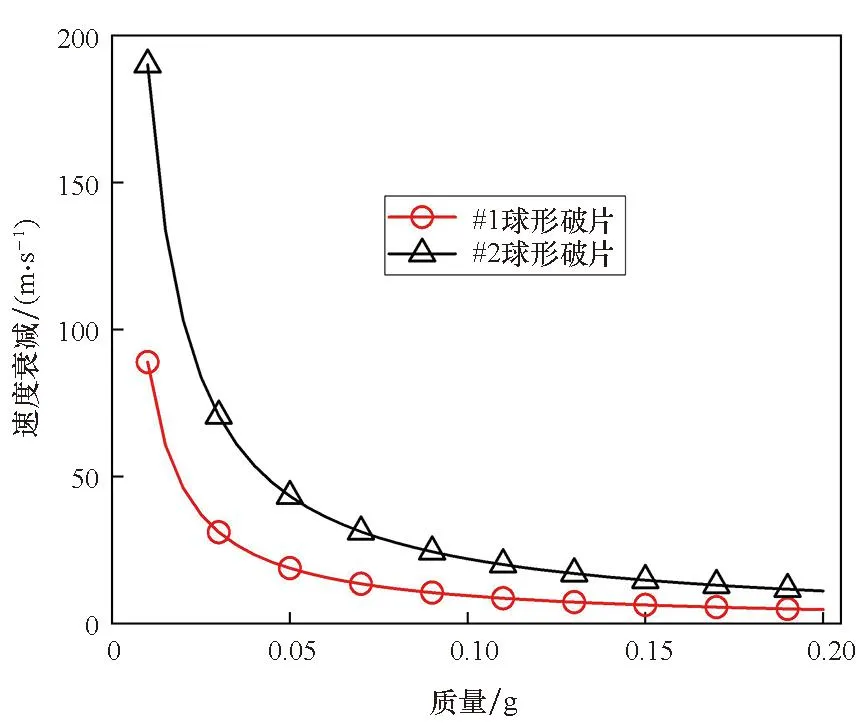
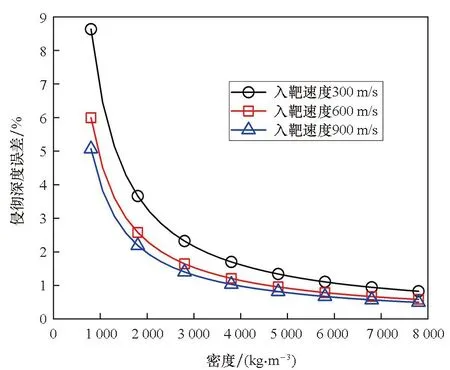
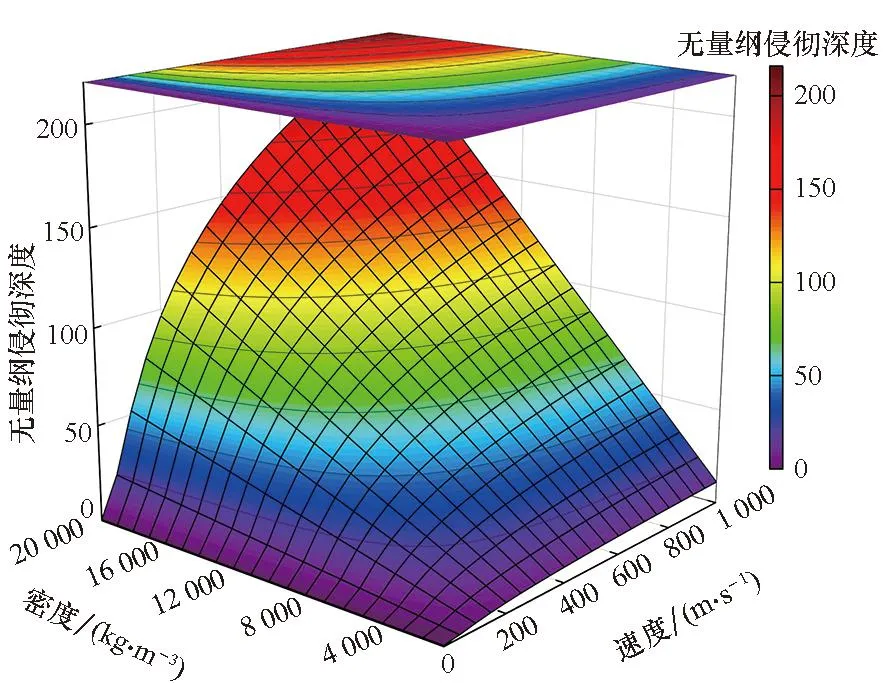
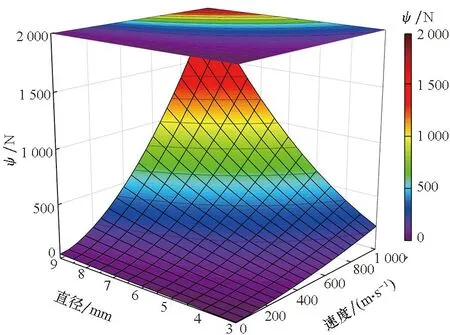
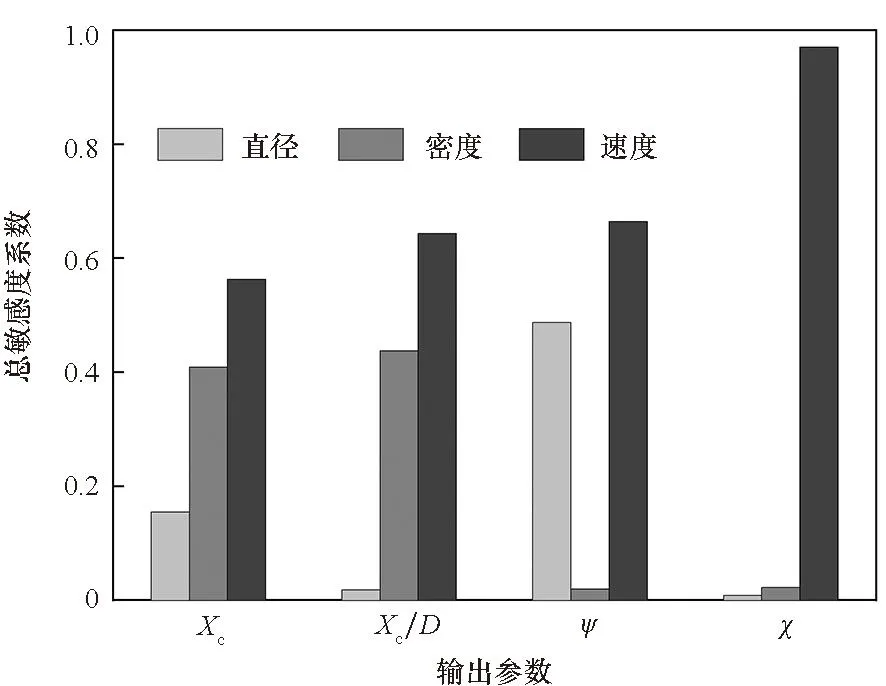
假設球形破片侵徹明膠過程中,僅破片的前半球面與明膠接觸作用,則球形破片侵徹明膠的過程可分為兩個階段:未完全侵入階段和完全侵入階段。在未完全侵入階段,-R 將式(6)~(8)代入式(1)并積分,得到球形破片在兩個階段的運動阻力F為: (10) 式中,vn為微元的法向速度,vn=v·n=v·x/R。 根據牛頓第二定律,球形破片的運動方程可表示為: (11) 其中,m是球形破片的質量。 第一階段:球形破片所受的阻力與位移相互關聯耦合,難以求出位移的解析解。令ve為球形破片的前半球面剛好完全進入明膠時的速度,第一階段結束時,球形破片速度由入靶速度v0衰減為ve,侵徹明膠深度Xc1=R。 第二階段:球形破片的前半球面完全進入明膠后,其阻力形式相對簡單,聯立式(10)和式(11),有如下關系: (12) 式中,m=ρp4πR3/3,R=D/2,ρp為球形破片密度,D為球形破片直徑。將m代入式(12)可得: (13) 將式(13)移項,并對兩邊同時積分可得: (14) 對式(14)進行化簡,可得球形破片在第二階段位移xc2的表示式為: (15) 特別地,當球形破片速度v衰減為0時,即第二階段結束時,球形破片在明膠中的侵徹深度Xc2為: (16) 球形破片在明膠中總的侵徹深度Xc=Xc1+Xc2,引入無量綱侵徹深度Xc/D: (17) 式(17)給出了剛性球侵徹軟介質類靶標的一般表達式,具有普適性。若只考慮球形破片在第二階段的動能損失,定義符號ψ為球形破片在單位侵徹距離上的動能損失,其表達式為: (18) 定義符號χ為第二階段球形破片在單位侵徹距離上的比動能損失,其表達式為: (19) 式中,ΔEsk2代表球形破片在第二階段的比動能損失,ΔEsk2=ΔEk2/Smax,其中Smax代表球形破片的最大橫截面積,Smax=πD2/4。 將照相明膠顆粒與自來水按1 ∶9重量配比,置于恒溫60 ℃的水浴爐中保溫1 h,然后將澄清透明的明膠溶液注入尺寸為350 mm×250 mm×200 mm的不銹鋼模具中,待冷卻至室溫后放置在4 ℃的恒溫箱中保溫24 h,最后脫模后再保溫2 h,即可進行球形破片侵徹明膠的實驗。 為了便于發射球形破片,需要將其放置在塑料彈托中,如圖2所示,并用黃油填滿彈托的縫隙,然后將彈托裝入帶發射藥的7.62 mm槍彈藥筒中,使用彈道槍瞄準明膠中心位置進行垂直射擊。射擊時,通過光電靶測量球形破片進入明膠前的速度,光電靶的中心與明膠的距離為1 m,光電靶之間的距離為1.2 m。高速攝像機用于拍攝球形破片在明膠中的運動過程,拍攝幀率為10 000幀/s,分辨率為640×320 px。實驗系統示意圖如圖3所示,其中明膠側面的光源用于提高拍攝畫面的質量。 圖2 用于發射球形破片的彈托Fig.2 Sabots used to fire spherical fragments 圖3 實驗系統示意圖Fig.3 Schematic diagram of the experimental system 實驗中各發射了三種不同直徑的鋼質球形破片,破片編號為#1~#3,其直徑D、質量m和通過光電靶的時間差Δt如表1所示。三種球形破片侵徹明膠的運動過程如圖4所示,可見球形破片在明膠中的運動可視為水平直線運動,其在豎直方向的運動可忽略不計。使用圖像后處理軟件的測量功能,可獲得球形破片的位移隨時間的變化規律。 表1 球形破片的參數 (a) #1球形破片的侵徹過程(a) Penetration process of the #1 spherical fragment (b) #2球形破片的侵徹過程(b) Penetration process of the #2 spherical fragment (c) #3球形破片的侵徹過程(c) Penetration process of the #3 spherical fragment 根據表1中球形破片通過光電靶的時間和光電靶之間的距離,求得#1~#3球形破片入射明膠的入靶速度分別為651 m/s、712 m/s和931 m/s。 令實驗中#i球形破片進入明膠中第1幀對應的時刻為Ti1,則第j幀對應的時刻Tij為: Tij=Ti1+dt×(j-1) (20) 式中,dt為高速攝像機的拍攝間隔。 令Tij時刻球形破片位移的實驗值為pij,理論計算值為yij,則位移的實驗值和理論值的均方根誤差總和σ為: (21) 式中,ni為#i球形破片的有效實驗數據個數。 為使運動模型能夠較好地模擬所有球形破片的運動規律,阻力系數A和B的取值要使σ最小。已知明膠材料的密度ρt=1 030 kg/m3,屈服強度Y=2.2×105Pa[7],使用式(10)~(11)和位移的實驗數據,借助四階龍格-庫塔法和直接結果搜索法,編程求解阻力系數。經計算,最優的阻力系數為A=2.77,B=0.34。 球形破片位移的實驗值和理論值的比較如圖5所示,可以看出實驗值與理論模型計算值誤差很小,說明分段運動模型能較好地模擬不同直徑的鋼質球形破片侵徹明膠的運動規律。 圖5 位移的實驗值和理論值的比較Fig.5 Comparison between theoretical and experimental displacements 以同樣的實驗方法測試直徑5.16 mm、質量1.39 g的鎢球侵徹明膠的運動位移,光電靶測得鎢球入射明膠的入靶速度為800 m/s。鎢球破片位移的實驗值和理論值的比較如圖6所示,說明分段運動模型能夠有效預測不同密度的球形破片侵徹明膠的運動規律,具有普適性。 圖6 鎢球的運動位移Fig.6 Motion displacements of the tungsten ball 本文使用的#1~#3球形破片入射明膠的入靶速度v0是通過光電靶測得的,速度ve是通過式(10)~(11)計算得到的,表2比較了兩種速度之間的差距。速度v0和ve之間的差距是由于球形破片在未完全侵入階段的速度衰減,當前實驗條件下球形破片在未完全侵入階段的速度衰減為6~10 m/s。多數學者認為的球形破片在明膠中運動的初始速度實際是ve,而他們大都采用光電靶測得的入靶速度v0來替代,這樣就在初始速度的取值上產生了誤差,導致位移的計算結果往往不夠準確。 表2 球形破片在不同時刻的速度 球形破片在未完全侵入階段的速度衰減受破片直徑D、入靶速度v0和質量m的影響。圖7為#1和#2球形破片以不同入靶速度沖擊時,在未完全侵入階段的速度衰減。可見隨著入靶速度的增加,不同直徑的鋼質球形破片的速度衰減均呈線性增加,約占入靶速度的1%。 圖7 入靶速度對未完全侵入階段速度衰減的影響Fig.7 Effect of entering-target velocity on velocity attenuation in the incomplete entering stage 不同質量的#1和#2球形破片,以入靶速度650 m/s沖擊時,在未完全侵入階段的速度衰減如圖8所示。當直徑相同時,質量越小,即密度越低,速度衰減越大,當密度特別低時,球形破片在未完全侵入階段的速度衰減可達幾十到上百米每秒;當質量相同時,大直徑低密度的球形破片速度衰減大于小直徑高密度的球形破片,但隨著密度的增加,兩者之間的差距在逐漸減小。結果表明:密度對球形破片在未完全侵入階段的速度衰減影響較大,低密度的球形破片在未完全侵入階段的速度衰減將不能忽略。 圖8 質量對未完全侵入階段速度衰減的影響Fig.8 Effect of mass on velocity attenuation in the incomplete entering stage 球形破片在未完全侵入階段存在速度衰減,考慮和忽略此階段的運動模型在計算侵徹深度上存在誤差。未完全侵入階段對侵徹深度的影響規律如圖9所示。相同密度下,低入靶速度破片的侵徹深度誤差大于高入靶速度破片;相同入靶速度下,密度較低的破片侵徹深度誤差較大,隨著破片密度的增加,侵徹深度誤差逐漸減小。入靶速度為600 m/s時,密度為7 800 kg/m3(鋼)的破片侵徹深度誤差約為0.6%,而密度為1 000 kg/m3(高聚物)的破片侵徹深度誤差約為4.5%。結果表明:低密度、低入靶速度的球形破片忽略未完全侵入階段對侵徹深度的影響較大。 圖9 未完全侵入階段對侵徹深度的影響Fig.9 Effect of the incomplete entering stage on penetration depth 由上文的分析可知,球形破片的參數直徑D、密度ρp和入靶速度v0均會對侵徹明膠的過程產生影響,首先用理論推導分析球形破片參數對侵徹深度等參數影響的敏感性。將已知的相關參數代入式(17)~(19),發現Xc/D是與球形破片密度ρp、初始速度ve相關的函數;ψ是與球形破片直徑D、初始速度ve相關的函數;而χ是只與初始速度ve相關的函數。通過進一步的量綱分析可知,ψ反映了球形破片侵徹明膠過程中的平均阻力;χ則反映了球形破片表面微元侵徹明膠過程中的平均阻抗應力。 為了更直觀地判斷球形破片參數密度ρp、直徑D和速度ve對參數Xc/D、ψ影響的敏感性,根據適用于侵徹明膠的輕武器彈藥的相關性能指標[26],取密度ρp變化范圍為1 000~20 000 kg/m3,直徑D的變化范圍為3~9 mm,速度ve的變化范圍為0~1 000 m/s,作三維空間曲面圖來分析。圖10給出了Xc/D在(ρp,ve)平面上的變化,顯然,無量綱侵徹深度對速度ve更敏感而非對密度ρp更敏感。圖11給出了ψ在(D,ve)平面上的變化,可以看出球形破片侵徹明膠過程中的平均阻力也對速度ve更敏感。此外,圖10~11中三維曲線頂部的等高線可用于指導球形破片的參數優化設計。 圖10 無量綱侵徹深度Xc/D在(ρp,ve)平面上的變化Fig.10 Variation of dimensionless penetration depth Xc/D on (ρp,ve) plane 圖11 參數ψ在(D,ve)平面上的變化Fig.11 Variation of parameter ψ on (D,ve) plane 在理論公式特別復雜的情況下,有時無法求出位移的解析解,還可以借助Sobol′法來分析各因素的敏感性。Sobol′法是一種廣泛應用于全局敏感性分析的算法[27],可用基于方差的蒙特卡羅法,通過采樣計算模型響應的總方差及各項偏方差,從而求得敏感性[28]。Sobol′法的主要思想是:令輸入變量的定義域為單位空間,即Ωk=(x|0≤xi≤1;i=1,…,k),將函數f(x1,…,xk)分解成2n項多級函數的總和,即: f1,2,…,k(x1,…,xk)] (22) 然后求解f(x1,…,xk)的總方差: (23) 式(22)中其他項的偏方差表示為: (24) 敏感度系數定義為式(24)與式(23)的比值: (25) 對式(23)兩邊同時除以D,可以推導出: (26) 其中,Si稱為因素的一階敏感度系數,它代表因素xi對輸出的主要影響,即對方差的貢獻大小,根據此定義有: (27) 類似地,Sij(i≠j)被稱為二階敏感度系數,以評估xi和xj兩因素耦合作用對總體方差的影響。 同理,評估給定參數的主要影響和有關該變量的所有相互作用的總敏感度系數可以表示為: (28) 式中,~i表示不包含i。 利用式(27)~(28)配合四階龍格-庫塔法,再結合Sobol′法編程,求解輸入參數直徑D、密度ρp和速度ve對輸出參數Xc、Xc/D、ψ和χ影響的敏感度系數。圖12給出了各輸入參數對輸出參數影響的敏感度系數,系數值越大表明輸出參數對該因素越敏感,系數值特別小代表此因素對輸出參數影響微乎其微,即此因素與輸出參數不相關。由圖12可知,用Sobol′法計算的結果與上文理論分析得出的結論基本一致。敏感度系數的影響規律為:影響侵徹深度Xc的敏感度系數由大到小依次是速度、密度和直徑;影響無量綱侵徹深度Xc/D的敏感度系數由大到小依次是速度和密度,與直徑無關;影響平均阻力ψ的敏感度系數由大到小依次是速度和直徑,與密度無關;而平均阻抗應力χ只與速度相關。對比圖12(a)和圖12(b)可知,以輸出參數無量綱侵徹深度Xc/D為例,速度和密度的總敏感度系數均大于一階敏感度系數,表明這兩個因素關聯耦合影響的程度大于單一因素。因此,引入無量綱碰撞函數I和無量綱密度比λ,其表達式為: (29) 將式(29)代入式(17)可得: (30) 顯然,這兩個無量綱參數I和λ,控制并決定著剛性球侵徹明膠的深度,式(30)的形式同樣適用于剛性球侵徹其他軟介質類的情況。 (a) 一階敏感度系數(a) First-order sensitivity coefficients (b) 總敏感度系數(b) Total sensitivity coefficients 本文為揭示球形破片對人體組織致傷機理,通過理論分析的方法,開展球形破片侵徹明膠的研究。基于動態空腔膨脹理論,考慮球形破片未完全侵入階段的速度衰減,建立了球形破片侵徹明膠的分段運動理論模型,并通過實驗進行驗證。分析了理論計算過程中的誤差來源,并推導得到了無量綱侵徹深度的表達式。利用Sobol′法進行了球形破片參數(直徑、密度和速度)對侵徹深度等參數影響的敏感性分析。得出以下結論: 1)理論模型和實驗結果符合較好,表明本文所建立的運動模型能較好地描述球形破片侵徹明膠的運動規律; 2)未完全侵入階段的速度衰減與破片的密度密切相關,鋼質球形破片的速度衰減約為入靶速度的1%,破片密度較低時速度衰減較大,不可忽略; 3)理論方法和Sobol′法對破片參數的敏感性分析規律基本一致,破片參數對侵徹深度影響的敏感性由高到低依次是速度、密度和直徑。 本文推導的侵徹深度公式,可為殺傷元參數優化設計和毀傷評估提供理論參考。 致謝 63961部隊的陳川琳工程師,在Sobol′法的算法上提供了幫助和指導,謹致謝意!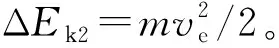
2 實驗方法與結果




3 結果討論
3.1 阻力系數確定
3.2 模型驗證及誤差分析
3.3 破片參數的敏感性分析
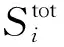

4 結論

