基于權(quán)重的AHP判斷矩陣一致性調(diào)整方法

耿正霖,吳佳妮,程興華,包長春

(國防科技大學(xué) 氣象海洋學(xué)院, 湖南 長沙 410073)

層次分析法[1](analytic hierarchy process,AHP)是一種綜合定性與定量分析的多指標、多準則的綜合評價方法,為定量分析定性事件提供了一種有效的技術(shù)手段,在經(jīng)濟、社會、管理、軍事等諸多領(lǐng)域得到了廣泛應(yīng)用[2-8]。其基本原理是由決策者(decision maker, DM)對不同指標進行兩兩比較,構(gòu)建一個判斷矩陣(pairwise comparison matrix, PCM),通過判斷矩陣進行分析得出不同指標的權(quán)重[1]。判斷矩陣描述了決策者對不同比較因素的判決,但該判斷通常有主觀性,可能出現(xiàn)前后不一致的情況,即構(gòu)造出來的判斷矩陣可能不滿足一致性要求[9-10],導(dǎo)致計算出的權(quán)重難以保證決策的可靠性。因此,計算權(quán)重前通常需對判斷矩陣進行一致性檢測和元素值調(diào)整與修正,減小主觀不一致對決策造成的影響。

目前,對判斷矩陣進行修正,通常考慮兩點:①使得改進后的判斷矩陣滿足一致性要求;②盡量保證對原始判斷矩陣的修改不違背決策者的初衷。也就是在保證判斷矩陣滿足一致性要求的前提下,調(diào)整判斷矩陣的元素值,使得調(diào)整后的判斷矩陣與原始判斷矩陣的差異程度最小[11]。這里所說的判斷矩陣滿足一致性要求,通常是指判斷矩陣的一致性系數(shù)(consistency ratio,CR)小于0.1[1],該評判標準已廣泛用于AHP一致性評價中。而矩陣調(diào)整程度可采用不同的指標進行衡量[11],例如判斷矩陣各元素總的變化量[12]、判斷矩陣各元素調(diào)整最大值[11,13]、判斷矩陣調(diào)整元素個數(shù)[14]、判斷矩陣元素調(diào)整比例[15-16]等。這些方法均以CR滿足一致性要求為目標,通過不同評價指標對應(yīng)算法進行判斷矩陣的調(diào)整,直至判斷矩陣滿足一致性要求。

但是,目前對判斷矩陣信息保留程度的評價標準都是從判斷矩陣出發(fā),以判斷矩陣調(diào)整前后的變化量衡量對原判斷信息的保留程度,卻沒有考慮調(diào)整后判斷矩陣殘留的不一致性(CR≠0)對最終權(quán)重計算結(jié)果的影響。因為當CR≠0時,矩陣的邏輯不一致性[17]可能并未完全消除,會導(dǎo)致計算權(quán)重時判斷矩陣還存在邏輯矛盾,而且矩陣的數(shù)值不一致性也會對權(quán)重計算產(chǎn)生影響。兩者都會使得權(quán)重所表述的各因素之間關(guān)系與原始判斷產(chǎn)生偏離,也就是說,目前的方法并不能完全衡量最終判斷結(jié)果(權(quán)重)對原始判斷矩陣的保留程度。

因此,本文從判斷結(jié)果出發(fā),提出一種基于計算權(quán)重的AHP一致性調(diào)整方法,以最終計算權(quán)重對應(yīng)的完全一致矩陣與原始判斷矩陣差異最小為優(yōu)化目標,進行判斷矩陣調(diào)整,使權(quán)重能最大程度保留原始判斷信息。

1 問題描述

通常,層次分析法的應(yīng)用過程如圖1所示。

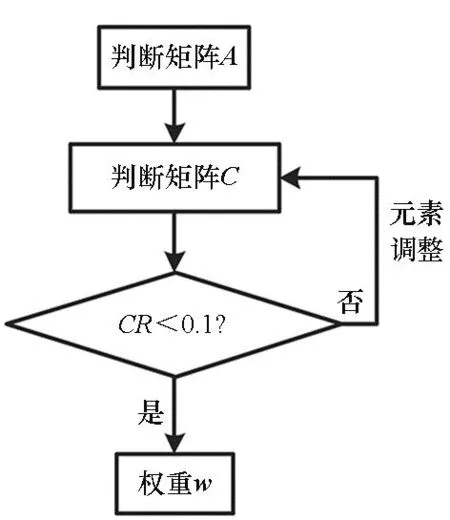
圖1 層次分析法應(yīng)用過程Fig.1 Process of AHP application

首先,決策者給出原始判斷矩陣A,將A作為矩陣調(diào)整的初始值賦值給C,若C滿足一致性要求(CR<0.1),則直接用C計算權(quán)重w;若C不滿足一致性要求,則通過相應(yīng)的準則進行矩陣調(diào)整,直至C滿足一致性要求(CR<0.1),再根據(jù)矩陣C計算對應(yīng)的權(quán)重w,以進行不同因素的重要性加權(quán)。

目前,大多文獻關(guān)注的是矩陣調(diào)整前后的變化量X(X=C-A),以矩陣調(diào)整量的相應(yīng)數(shù)據(jù)作為信息保留程度的衡量標準。但從層次分析法的應(yīng)用看,最終目的是計算權(quán)重w,要使結(jié)果盡量保留決策者的判斷,應(yīng)該使最終計算得到的權(quán)重w所表示的元素之間的重要性關(guān)系能盡可能保留原始判斷矩陣的信息,而不是調(diào)整后的矩陣C盡可能保留原始判斷矩陣的信息。

權(quán)重w可以視為是根據(jù)判斷矩陣所有元素得出的綜合判決的結(jié)果,包含了各因素之間的重要性判斷,其對應(yīng)一個完全一致的矩陣B(B滿足條件:對于任意的i,j,k,有bi,j=bi,kbk,j[18]),可以描述各因素兩兩之間的相對重要性。用完全一致矩陣B與原始判斷矩陣A的差異來衡量判斷矩陣元素調(diào)整對原始決策信息的保留程度更為合理。層次分析法過程中涉及的變量關(guān)系如圖2所示。

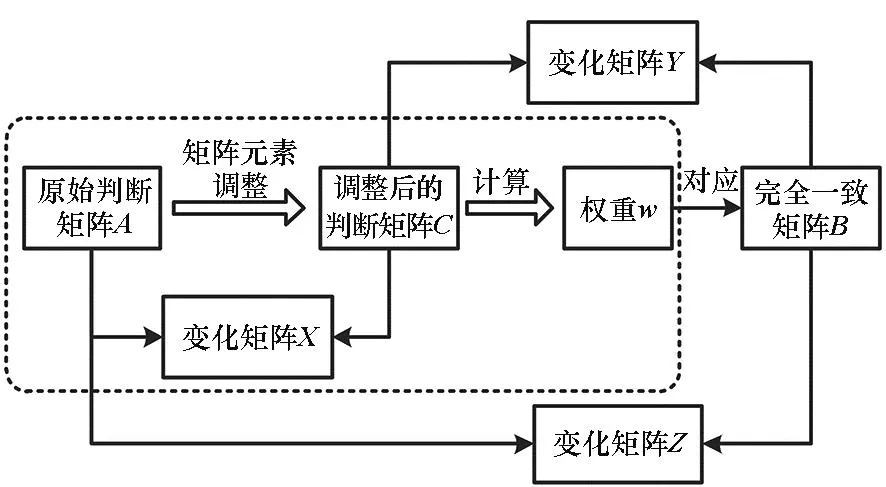
圖2 矩陣相互關(guān)系示意圖Fig.2 Schematic diagram of matrix interrelationships

在實際情況下,矩陣元素調(diào)整通常不能完全消除不一致性(CR≠0),此時,計算得到的權(quán)重所對應(yīng)的完全一致矩陣B與用于計算權(quán)重的判斷矩陣C存在差異,用矩陣Y表示(Y=B-C),該矩陣等效于將判斷矩陣C進行調(diào)整得到一個完全一致矩陣B所進行的調(diào)整量。那么,權(quán)重所對應(yīng)的完全一致矩陣B與原始判斷矩陣存在的差異為矩陣X和Y的疊加,用矩陣Z表示,即Z=B-A。

可以看出,矩陣X是調(diào)整后的判斷矩陣C相對于原始判斷矩陣的改變量,而矩陣Z才是最終判斷結(jié)果相對于原始判斷矩陣的改變量。所以,通過矩陣Z更能衡量出判斷結(jié)果即權(quán)重w對原始判斷矩陣的改變程度或保留程度。因此,本文以矩陣Z各元素的平方和作為矩陣改變量的衡量標準,以其最小值為優(yōu)化目標進行矩陣B的求解。

(1)

式中,N為元素個數(shù)。

此時,權(quán)重求解過程轉(zhuǎn)化為求解一個完全一致矩陣,使其與原始判斷矩陣差異最小的過程。這個完全一致矩陣與權(quán)重一一對應(yīng),求出矩陣就對應(yīng)得到權(quán)重。權(quán)重w和完全一致矩陣B對應(yīng)關(guān)系如下:

1)設(shè)w=[w1,w2,…,wN]T,則B可以由式(2)計算得到。

(2)

2)若已知完全一致矩陣B,則對其任意列進行歸一化即可得到權(quán)重w。

(3)

從上述分析可知,本文目標就是通過矩陣元素調(diào)整,構(gòu)造一個完全一致矩陣,使其相對于原始矩陣的改變量最小。

2 算法步驟

假設(shè)原始判斷矩陣為A,表示為:

(4)

本文目的是求得一個完全一致矩陣B,使得A與B的差異最小,而B的任意列進行歸一化后作為該判斷矩陣計算得到的權(quán)重。這一過程也可以理解為一個帶約束條件的優(yōu)化問題:在保證最終結(jié)果為完全一致矩陣的條件下,使求得的矩陣與原始判斷矩陣的差異程度最小。

顯然,對于一個完全一致矩陣B,其秩為1,行列間相關(guān),僅有N-1個獨立的變量,只要確定N-1個獨立的變量的值就能確定整個矩陣。不失一般性,可假設(shè)N-1個獨立的變量為bm,m+1,其中1≤m≤N-1,則矩陣其他元素都可由這N-1個元素計算得到。矩陣B可依據(jù)式(5)構(gòu)造:

(5)

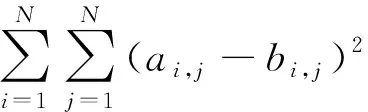
(6)

因為ai,i=bi,i=1,式(6)等效于:

(7)

要得到使得式(7)最小的bm,m+1(1≤m≤N-1),最簡單的方式是通過在一定范圍內(nèi)遍歷bm,m+1的取值,但該方法計算量較大,特別是當N較大時,若每個維度遍歷數(shù)為M,總的遍歷數(shù)量為MN-1。基于此原因,利用梯度最速下降法進行最優(yōu)值的求解,主要步驟如下。

2.1 優(yōu)化目標

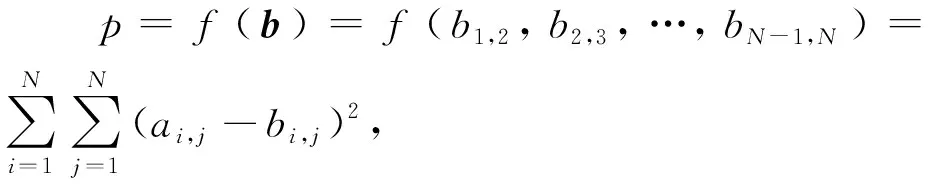
2.2 梯度計算

計算p=f(b)的梯度,上式可以寫為:

(8)

其中,bi,j對bn,n+1(1≤n≤N-1)求導(dǎo)得:

(9)

那么,計算得到1/bi,j對bn,n+1(1≤n≤N-1)求導(dǎo)的結(jié)果:

(10)

則可計算出p對bn,n+1(1≤n≤N-1)的導(dǎo)數(shù):

(11)

那么,可根據(jù)式(11),求得p的梯度:

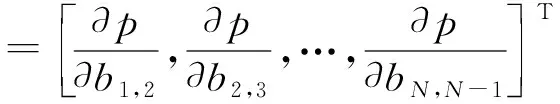
(12)

2.3 數(shù)據(jù)更新

傳統(tǒng)梯度下降法對每一個參數(shù)的學(xué)習(xí)率是相同的,但實際中,不同參數(shù)的重要性不同,因此本文采用自適應(yīng)梯度算法[19](adaptive gradient algorithm,AdaGrad)進行數(shù)據(jù)更新,對不同參數(shù)采用不同的學(xué)習(xí)率,使目標函數(shù)能更快收斂。

設(shè)梯度累計量為r,k表示迭代次數(shù),k≥1,初始化r(0)=0,累計量的更新公式如下:

r(k)=r(k-1)+H(?(k),?(k))

(13)

式中,H(?(k),?(k))表示?(k)和自身的Hadamard乘積。梯度的更新公式如下:

(14)

式中:γ為學(xué)習(xí)率;δ為一個極小量,避免分母為0。因為原始判斷矩陣元素在[1/9,9]內(nèi)分布,b初值各個元素也在[1/9,9]內(nèi)分布,為避免調(diào)整量過大,可控制γ大小使得最大調(diào)整量在一定的范圍內(nèi)。

可以看出,AdaGrad算法第一次調(diào)整值約為學(xué)習(xí)率,如果學(xué)習(xí)率超過了初值或者很接近初值,會導(dǎo)致調(diào)整后的元素接近于0,其對應(yīng)的倒數(shù)值會很大,使得結(jié)果不收斂或者收斂到錯誤結(jié)果。故初值和學(xué)習(xí)率的選擇原則為:

1)采用原始判斷矩陣的次對角陣元素為初值;在無其他信息時,原始判斷矩陣具有較高的參考價值。

2)學(xué)習(xí)率的選擇,可根據(jù)初值元素中的最小值設(shè)定,為避免調(diào)整后特別是首次調(diào)整后矩陣元素接近0,設(shè)置學(xué)習(xí)率為最小元素值的1/2。

2.4 迭代計算

計算b(k)對應(yīng)的p(k),當|p(k)-p(k-1)|<ε停止迭代,其中ε為一個很小的正數(shù)。假設(shè)此時迭代次數(shù)為K,以此時的b(K)作為b的最終解。

2.5 權(quán)重計算

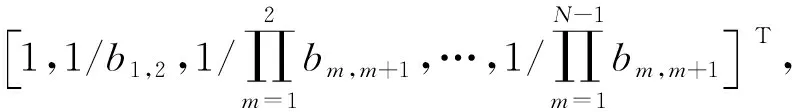
(15)

通過上述方法,可以根據(jù)梯度大小自動調(diào)整變化量的大小和方向,加快矩陣調(diào)整速率,使得b較快收斂到最小值點,得到改變量較小的矩陣B,同時得到對應(yīng)的權(quán)重w。

3 算例分析

利用MATLAB對上述算法進行驗證分析,并與其他幾種參考算法進行比較。計算經(jīng)典算例下本文所述的完全一致矩陣改變量大小,以此衡量算法的性能。傳統(tǒng)算法通常只計算得到一個滿足一致性條件的判斷矩陣,進而計算權(quán)重;本文利用權(quán)重計算其對應(yīng)的完全一致矩陣,將其與原始判斷矩陣進行比較。進行比較的算法如表1所示。

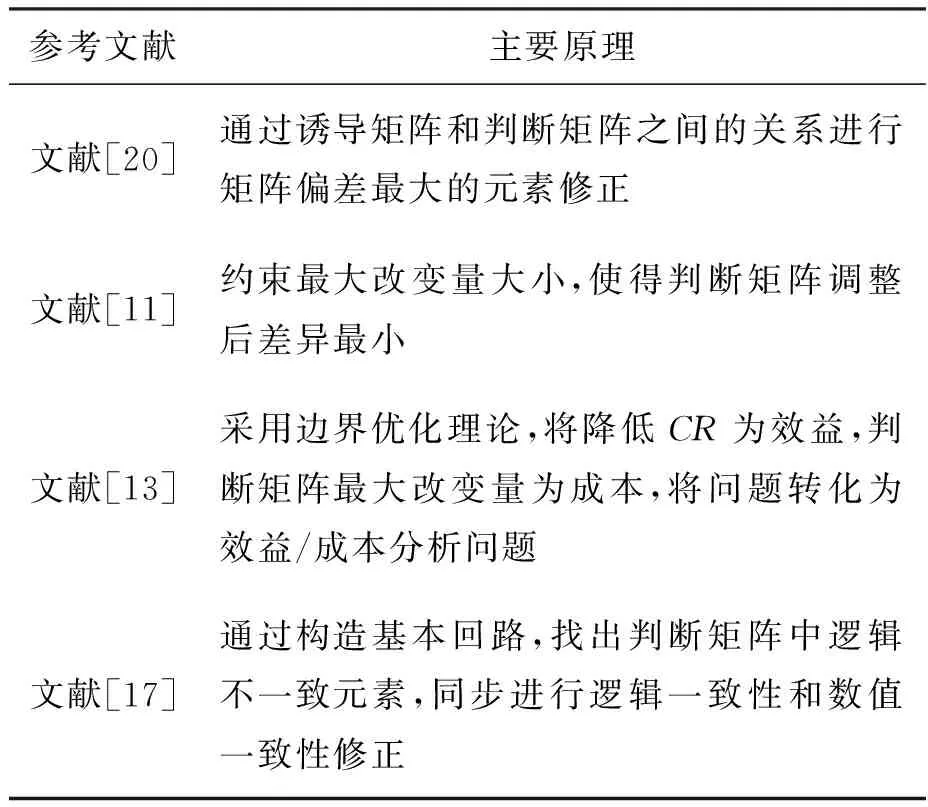
表1 主要比較算法

3.1 算例1

文獻[20]、文獻[11]和文獻[13]均通過算例1進行算法性能的比較,其初始判斷矩陣為:

3.1.1 文獻[20]方法

文獻[20]所述方法得到的調(diào)整后的判斷矩陣為:

計算得到權(quán)重及對應(yīng)的完全一致矩陣為:

將其與原始判斷矩陣進行比較,總的改變量為54.981 7,最大改變量為6.996 7(a2,3)。

3.1.2 文獻[11]方法

采用文獻[11]所述方法得到的調(diào)整后的判斷矩陣為:

計算得到權(quán)重及對應(yīng)的完全一致矩陣為:

將其與原始判斷矩陣進行比較,總的改變量為32.061 5,最大改變量為4.052 7(a2,3)。

3.1.3 文獻[13]方法

采用文獻[13]得到調(diào)整后的判斷矩陣為:

計算得到權(quán)重及對應(yīng)的完全一致矩陣為:

將其與原始判斷矩陣進行比較,總的改變量為31.003 3,最大改變量為4.312 7(a2,3)。

3.1.4 本文方法

設(shè)小常數(shù)δ為10-7,循環(huán)停止條件ε為10-5,本文方法不同條件計算得到的結(jié)果如表2所示。

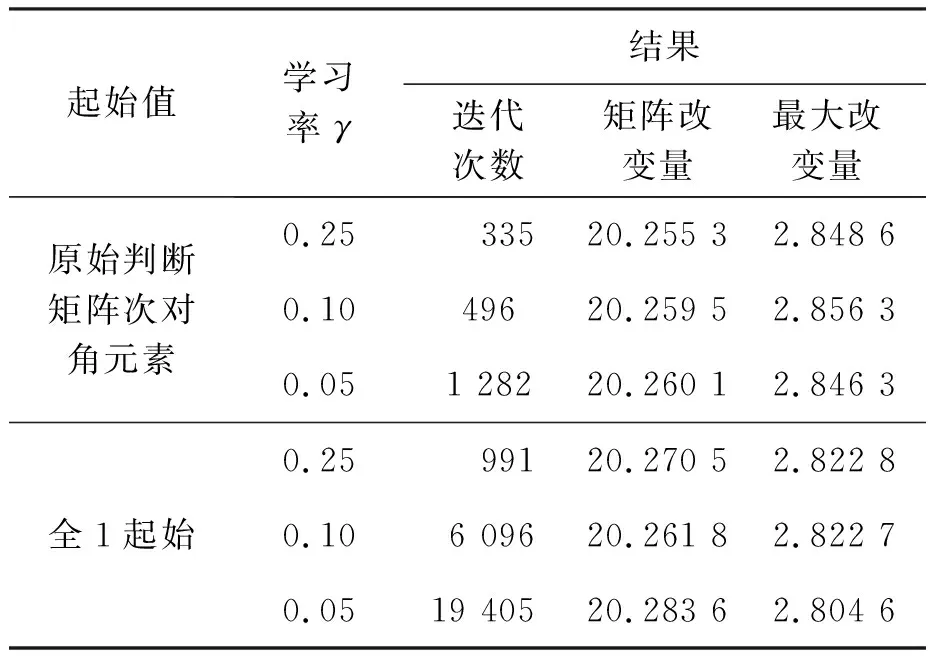
表2 算例1本文方法計算結(jié)果

從表2中結(jié)果看,不同的初值對最終的結(jié)果影響較小;隨著學(xué)習(xí)率的下降,迭代次數(shù)增加。其總的矩陣改變量相比其他方法顯著減小,最大改變量為a1,4。這里以表中條件1(起始值為原始判斷矩陣次對角元素,γ=0.25)和條件4(起始值為全1矩陣,γ=0.25)的結(jié)果進行分析,其余條件下計算結(jié)果與之相似。

第1種條件下,對應(yīng)完全一致矩陣為:

計算得到權(quán)重為:

參數(shù)收斂情況如圖3所示。

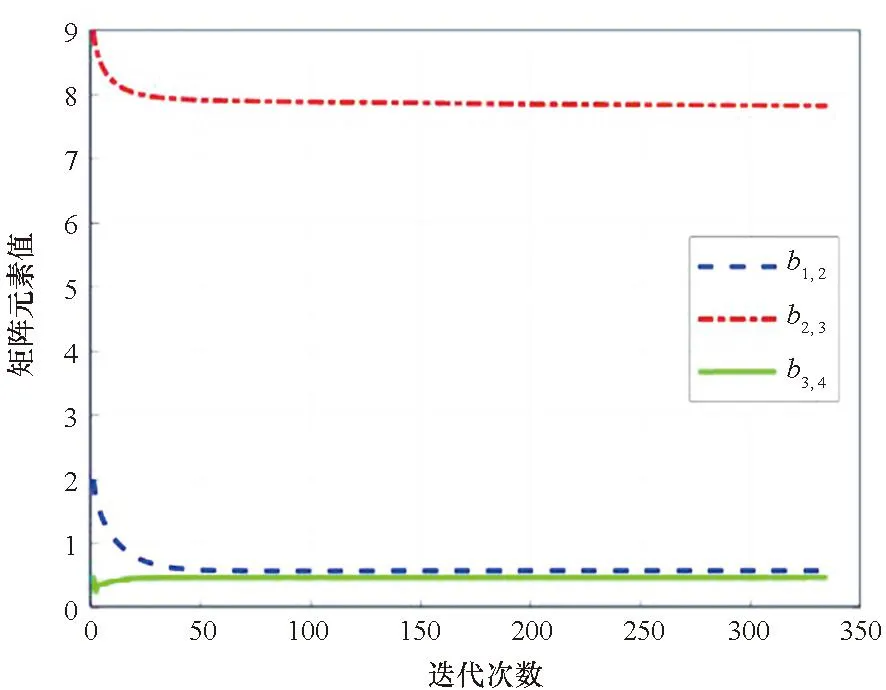
圖3 條件1參數(shù)收斂情況Fig.3 Convergence of parameters in case 1

第4種條件下,對應(yīng)完全一致矩陣為:

計算得到權(quán)重為:

參數(shù)收斂情況如圖4所示。

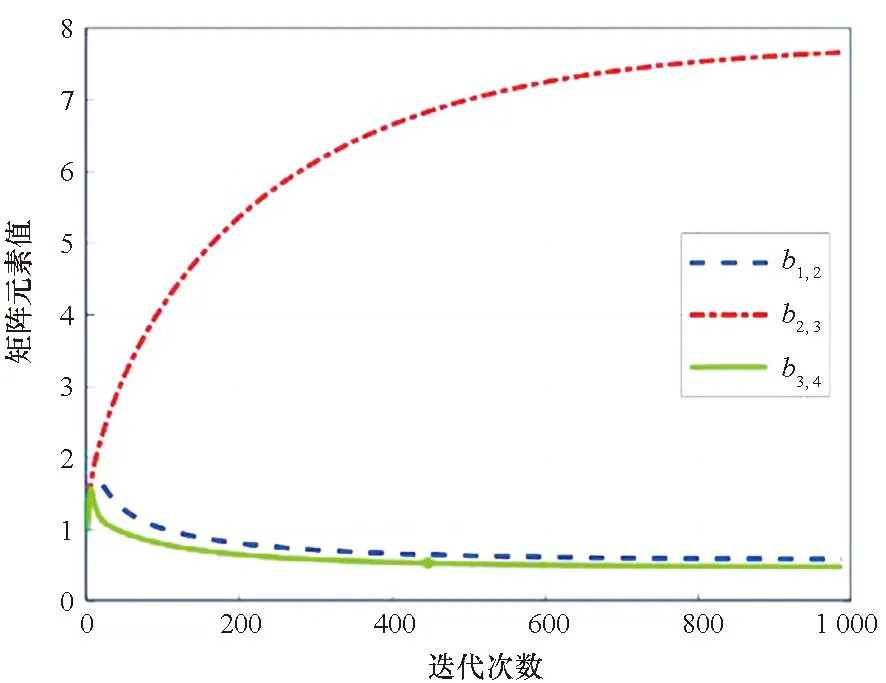
圖4 條件4參數(shù)收斂情況Fig.4 Convergence of parameters in case 4

取不同起始值時權(quán)重差值為:

可以看出,不同的起始值條件下,隨著迭代計算,b逐漸收斂到最終結(jié)果,兩種情況下最終得到的權(quán)重差異很小。但采用全1列向量作為初始值時,其與收斂結(jié)果的差距較大,迭代次數(shù)較多。

3.2 算例2

以參考文獻[13]和文獻[17]采用的算例進行算法的比較。原始判斷矩陣為A2。下面對幾種典型方法的計算結(jié)果進行比較。

3.2.1 基本回路法[17]

根據(jù)文獻[17],采用基本回路法對判斷矩陣進行修改,得到修改后的矩陣為C5,該矩陣的CR=0.082 2,滿足一致性要求,矩陣總的改變量為34.642 9,最大改變量為5.537 4(a3,7);利用此矩陣,計算得到權(quán)重,再得到對應(yīng)的完全一致矩陣B5,將其與原始判斷矩陣進行比較,總的改變量為224.428 1,最大改變量為9.854 7(a8,4)。

3.2.2 邊界優(yōu)化法[13]

采用邊界優(yōu)化法進行修改后的矩陣為C6,此時,矩陣的CR=0.099 8,滿足一致性要求,總的改變量為13.103 8,最大改變量為0.718 6(a8,2);雖然矩陣的改變量很小,但此時的CR是相對較大的,說明此矩陣存在較大的不一致性,即判斷存在一定的矛盾,以此得出的權(quán)重可靠性不高。此外還可以看出,調(diào)整后a3,7邏輯不一致并未改善。以此矩陣計算權(quán)重,得到其對應(yīng)的等效完全一致矩陣B6,相對于原始判斷矩陣,總的改變量為242.358 5,最大改變量為10.228 7(a8,4)。

3.2.3 本文方法

本文計算了不同參數(shù)條件下本文方法的計算結(jié)果,得到對應(yīng)的迭代次數(shù)、矩陣改變量以及完全一致矩陣。其中設(shè)小常數(shù)δ為10-7,循環(huán)停止條件ε為10-5。結(jié)果如表3所示。

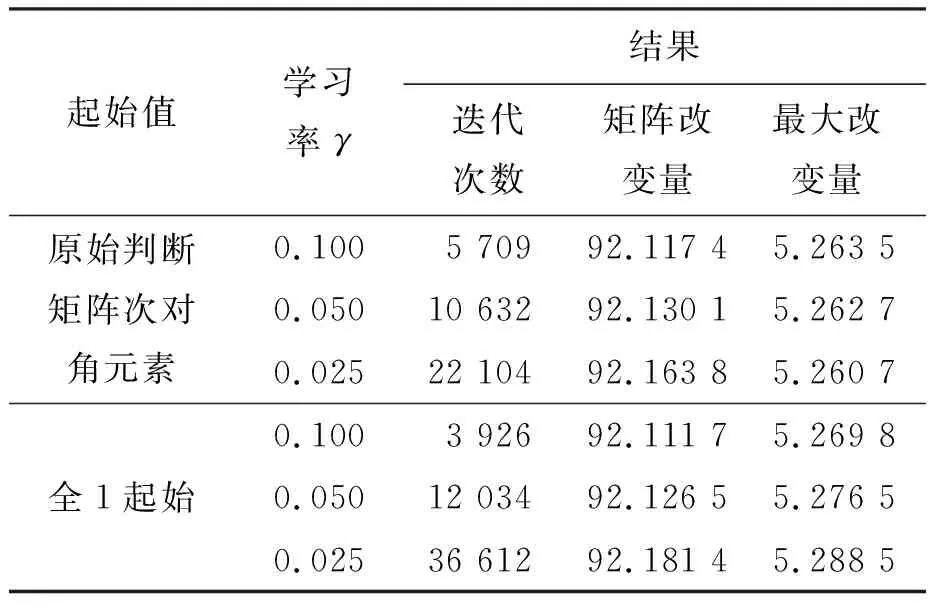
表3 算例2本文方法計算結(jié)果

不同條件下計算結(jié)果近似,僅迭代次數(shù)隨學(xué)習(xí)率的減小而增加,這里取條件1(起始值為原始判斷矩陣次對角元素,γ=0.100)和條件4(起始值為全1矩陣,γ=0.100)的結(jié)果進行分析,其余條件下的結(jié)果不再贅述。

條件1下,計算得到的完全一致矩陣如下B7,1所示;條件4下,計算得到的完全一致矩陣如下B7,2所示。

可以看出,選擇不同的迭代初值,對最終收斂結(jié)果影響較小,以等效完全一致矩陣的改變量為衡量標準,用本文方法計算得到的矩陣總的改變量約為92,最大改變量約為5.3,遠小于基本回路法和邊界優(yōu)化法的結(jié)果,可見本文方法更能保留原矩陣的信息。

4 結(jié)論

本方法通過權(quán)重構(gòu)建一個完全一致矩陣,將其與初始判斷矩陣進行擬合,采用梯度下降法求得矩陣調(diào)整量最小的完全一致矩陣,最大程度保留了原始判斷矩陣信息。該方法在限定最終得到的矩陣為完全一致矩陣的條件下進行,得到的結(jié)果同時滿足邏輯一致性和數(shù)值一致性。而且在計算過程中,不需要反復(fù)檢驗判斷矩陣是否滿足一致性要求,計算更為便捷。