基于電磁計算的同時極化雷達成像仿真

2024-04-11 07:40:12張云華

現代雷達 2024年2期

關鍵詞：信號

陳云,張云華*,李東

(1. 中國科學院國家空間科學中心微波遙感技術重點實驗室, 北京 100190) (2. 中國科學院大學電子電氣與通信工程學院, 北京 100049)

0 引言

極化雷達技術的發展豐富了雷達目標特征信息,形成各種新體制雷達更好地滿足目標高分辨檢測、成像、抗干擾、分類與識別等需求[1]。準確獲取以極化散射矩陣為代表的目標極化散射特性是極化雷達技術研究的重要內容,通常可采用分時極化和同時極化測量體制雷達獲取目標的極化散射矩陣[2-4]。所謂分時極化測量,是指雷達交替發射水平和垂直極化波形,同時接收兩種極化的回波信號;在該種體制下,以實際的脈沖雷達為例,至少需要發射水平極化和垂直極化兩個脈沖信號才能獲得極化散射矩陣的全部四個元素,因此目標運動去相關會對測量結果造成影響。而同時極化測量體制則是同時發射水平極化和垂直極化的雷達信號并同時接收兩種極化的回波信號,這樣只需發射一個脈沖信號便可獲得目標的極化散射矩陣,可降低目標運動對極化散射矩陣測量的影響[5-6]。1993年,文獻[2]提出使用了一對具有相反斜率的線性頻率調制(LFM)信號實現同時極化測量。文獻[3]針對經典極化學中“時諧性”或者“窄帶性”約束條件的局限性提出瞬態極化概念。2019年,文獻[7]將隨機信號與極化技術結合提出隨機極化新型探測技術,將信號的隨機性由最初的時、頻域拓展至極化域,降低波形的極化度,使得雷達具有更好的低截獲性能,其核心思想均是在兩正交極化通道上同時發射兩路平均功率相等的正交隨機波形。

雷達信號的模擬仿真是目標散射特性和雷達技術研究與發展的重要方面,尤其對于新體制雷達技術的研究具有重要價值,而雷達信號的電磁(EM)仿真可以獲得更加接近于實際的雷達回波信號,因而備受關注[8-10]。在雷達系統的研發或者對某一特定目標EM場特性的研究過程中,開展現場實驗和暗室測量不僅EM環境難以控制,而且過程復雜,成本較高;通過建立回波信號仿真模型,實現雷達目標回波信號的仿真,不僅在雷達系統的設計過程中至關重要,而且對數據進行進一步處理也發揮重要作用[11-12]。復雜目標的極化散射特性因包含各種散射機制難以通過點目標回波模型表示,其與真實目標的回波差異較大,不足以滿足當今新體制雷達研究需求[13];解決這個問題的一個很好的方法是通過EM計算工具(例如FEKO、HFSS或XFDTD)建立一個EM仿真模型較為精細地反映目標的散射特性,但必須指出的是這些工具不能直接獲取雷達目標時域回波信號[14-16],特別是基于目標散射特性的同時極化雷達目標回波仿真研究,尚未看到相關報道,因此,深入探究同時極化雷達目標回波仿真方法具有深遠的研究意義。

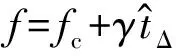
本文提出了一種基于EM計算的同時極化雷達(SPR)成像仿真方法。首先,基于FEKO建立目標的幾何模型,根據目標電尺寸等因素選擇合適的頻率步長構建目標全空間全極化寬帶EM散射特性數據庫[17];并采用完全互補序列(CCS)[18-19]設計正交性良好的低旁瓣同時極化波形; 然后,根據目標相對雷達視線的姿態角對數據庫進行插值調用,將同時極化發射信號與插值調用的極化散射數據進一步處理得到目標的時域回波信號。以F22為例進行了同時極化雷達的回波EM仿真,進而得到雷達圖像,并進行了Pauli分解及幅相誤差影響分析。該方法同時適用于其它體制、其它波形的回波仿真,對開展新體制雷達系統幅相特性、波形性能等研究具有重要的意義。

1 SPR回波信號模型及仿真方法

SPR系統如圖1所示,在不考慮雷達系統非理想因素的情況下,假設sH(t)、sV(t)分別表示同時極化雷達H極化通道和V極化通道的基帶信號,雷達發射信號可以表示為

(1)

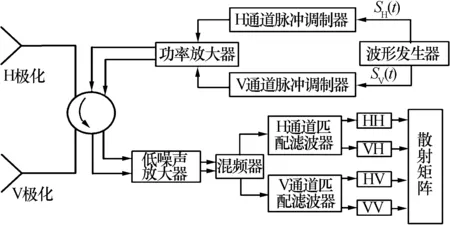
圖1 SPR系統框圖

式中：Tp為脈沖寬度;t為時間變量,0≤t≤Tp;fc為載波頻率;h和v分別為單位水平和垂直極化基; Rect(·)為矩形函數。

因此,發射信號的頻譜可以表示為

(2)

對于單個點目標的情況下,設雷達與點目標之間的距離為R(t),點目標的徑向速度為v(t),忽略EM波傳播過程中的能量損失,則點目標的射頻回波可以表示為

(3)

式中：β=(c-v(t))/(c+v(t))為縮放因子,表征目標速度對雷達波形進行了尺度調制;c為電磁波的傳播速度;τ為回波的時延。此時,可將雷達發射波與點目標的相互作用視為線性系統響應,當目標靜止時,系統函數為沖擊響應函數。

針對具有復雜EM極化散射特性的目標,可以將其極化散射特性看作系統響應函數h(t)。SPR射頻回波信號可表示為

(4)

式中：“*”表示卷積。由傅里葉變換的性質,可將h和v正交極化基下,復雜目標射頻回波信號對應的頻譜表示為

exp(-j2πfτ)

(5)

其中

為目標的EM極化散射特性,可以通過利用EM仿真工具計算獲取。因此,由傅里葉變換關系可將復雜目標的基帶回波信號表示為

(6)

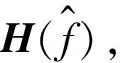
進一步考慮雷達系統的非理想特性,目標的測量散射矩陣M可以寫為

(7)

式中：f1和f2為極化通道的不平衡項;δi,i=1～4為雷達系統的串擾項;Nij(i,j為h或v)為各通道的附加噪聲項。同時極化雷達目標成像仿真流程如圖2所示,具體步驟如下：

圖2 SPR目標成像仿真流程

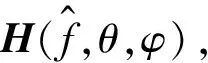
(2) 同時極化雷達波形設計。設計同時極化雷達波形sH(t)、sV(t),并引入發射通道非理想特性生成同時極化發射信號e(t)。

(3) 徑向運動對波形尺度調制后為e(βt),其中尺度調制可通過變采樣率實現,最后對e(βt)進行傅里葉變換得到G(f)=E(f/β)。

(4) 疊加目標EM極化散射特性并添加時延分量得到回波信號頻譜：R(f)=H(f)G(f)e-j2πfτ。

(5) 引入接收通道非理想特性后進行逆傅里葉變換,并模擬接收機熱噪聲,產生噪聲干擾下的目標回波,得到最終的時域回波信號

(8)

式中：n(t)為按照設定的信噪比(SNR)添加的高斯噪聲。

上述SPR目標回波仿真過程中,目標極化散射特性數據庫的構建只需依據目標的尺寸利用FEKO對較少的頻率采樣點進行EM計算,可以極大地減少EM散射計算量。

2 SPR波形設計

可用于SPR的常用正交雷達波形主要包括：“正負斜率LFM波形”、“正負斜率非LFM波形”、“正交多相編碼波形”等[20]。LFM信號脈沖壓縮后峰值旁瓣電平(PSL)為-13.26 dB。自適應濾波、加窗及其它技術可用于改善LFM波形的PSL;然而,這些方法將導致SNR損失和主瓣展寬[21];此外,通過駐定相位原理可以證明LFM信號的正交性受時間帶寬積的限制[22]。相位編碼波形具有較高的設計自由度,特別是CCS具有理想的相關特性,可用于產生正交性和旁瓣特性良好的SPR信號。本文基于優化最小化(MM)方法,采用CCS設計SPR波形[17],其波形可以表示為

(9)

式中：u1(n),u2(n)表示由CCS相位編碼;tb為碼元寬度;L為序列的碼長。假設雷達一個相關處理周期包含K個長度為N的恒模相位編碼,占空比為d,整個脈沖寬度為T=KNtb/d=Ltb/d。一對正交CCS可表示為

(10)

(11)

其中

(12)

可以將p1、p2視為(K,N)的CCS,K為脈沖數,N為序列長度。任意兩個CCS在滯后處的非周期性互相關可以定義為

i,j=1,2,k=1,…,K,n=0,… ,N-1

(13)

當i=j時,式(13)變為CCS的自相關函數。

為了設計具有良好自相關和互相關的序列,以互補積分旁瓣電平(CISL), 即自相關函數的旁瓣能量與互相關函數加權能量之和為代價函數,考慮如下優化問題

(14)

式中：ωn=ω-n≥0,n=0,…,N-1為不同時延的非負加權因子。優化問題式(14)中目標函數為非凸問題,由于序列采用互補結構,并且同時考慮了序列的自相關與互相關特性的優化,文獻[19]中提出的用于設計恒模單脈沖序列的積分旁瓣電平最小化算法不能被直接應用。針對優化問題式(14),令L=K(2N-1),并定義一個長度為2L的輔助序列

(15)

(16)

式中：vec(·)表示矩陣的矢量化;Un,n=1-L,…,L-1是L×L的Toeplitz矩陣,即

i,j=1,…,L-1

(17)

通過利用式(16),令Z=zzH,優化問題式(14)可以被重寫為

min vec(Z)HLvec(Z)-2ω0N2K2,
s.t. |z(n)|=1,n=1,…,2L

(18)

其中

(19)

由于ωk≥0,很容易發現為L非負的實對稱矩陣,且滿足Hermitian矩陣要求,因此可以利用MM方法處理優化問題式(18),同時達到對序列的自相關函數與互相關函數優化。

3 仿真試驗

為了驗證本文同時極化雷達目標成像仿真的有效性,選取圖3所示F22飛機(機長10.8 m、翼寬7.9 m、高度2.3 m),利用EM計算工具FEKO建立逆合成孔徑雷達(ISAR)轉臺模型。為了避免引起距離模糊,頻率步長需滿足Δf≤c/2E,其中E為目標的距離范圍。因此,以頻率步長Δf=0.01 GHz,Δθ(俯仰)=Δφ(方位)=1°,構建目標在0.8 GHz～1.8 GHz頻段的全空間全極化散射特性數據庫。圖4為目標在頻率為1.3 GHz處的全空間全極化RCS電磁散射特性。

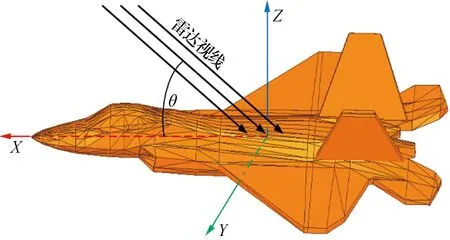
圖3 F22三維模型

圖4 F22模型全空間、全極化RCS特性(f =1.3 GHz)

設定發射的同時極化波形的載頻、脈寬和帶寬分別為Tp=10 μs,fc=1.3 GHz,B=280 MHz,采用本文所提出的方法設計碼長N=420、脈沖數K=5的CCS同時極化波形。波形如圖5所示,其自相關函數旁瓣和互相關函數均能達到-100 dB。

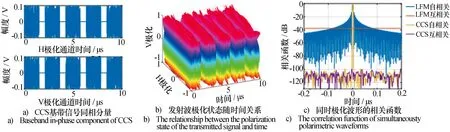
圖5 同時極化波形

(1) 同時極化雷達成像仿真

利用前面的仿真方法“裝配”了F22模型俯仰角θ=0°,方位角φ=-180°～180°,Δφ=1°的回波信號,仿真SNR為30 dB,暫不考慮雷達系統的非理想特性。圖6為目標回波信號進行匹配濾波后的一維距離像(HRRP);其中圖6a)～圖6d)為發射正負斜率LFM同時極化波時得到的HH、HV、VH和VV四個極化通道的HRRP,圖6e)～圖6h)為發射正交CCS同時極化波時對應四個極化通道的HRRP。很明顯,相比于正負斜率LFM,所設計的CCS同時極化波形有更好的旁瓣抑制。

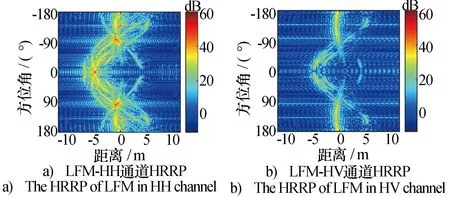
圖6 不同的SPR波形下F22 HRRP仿真對比

圖7給出了基于BP算法的ISAR成像結果,兩種波形的成像結果均表明同極化HH、VV通道的圖像輪廓清晰,尤其是頭部和飛機尾部具有更強的散射強度。另外,由于水平機翼較薄,其邊緣呈現水平偶極子特性,在HH極化通道中所產生的一次散射比VV通道中更強。垂直機翼邊緣在HH、VV極化中表現為弱散射體,在正負斜率LFM同時極化波中,由于波形具有較高的距離旁瓣,垂直機翼被尾部強散射體掩蓋, 而在CCS同時極化波中,由于波形良好的旁瓣特性從而可以清晰呈現垂直機翼。對于交叉極化圖像,強散射主要來自進氣孔、垂直機翼邊緣和尾部等復雜散射機制。但是,值得注意的是相同的圖像動態范圍內,圖7b)和圖7c) 中可發現水平機翼后邊緣存在交叉極化散射,而圖7f)和圖7g)中幾乎沒有出現。該差異進一步說明相比于正負斜率LFM波形,所設計的正交CCS同時極化波還具有更好的波形正交性,能精確獲取目標的極化散射矩陣。上述兩種波形的回波信號均體現了豐富的目標極化散射信息,而且回波信號的處理結果也反映了波形的性能差異,表明了本文所提出的同時極化雷達目標成像仿真方法具有較高的精度。

圖7 不同的同時極化雷達波形下F22 ISAR成像仿真對比

(2) 極化通道非理想特性仿真

由極化散射矩陣可以獲得與目標有關的極化信息,前面的分析沒有考慮極化通道非理想特性,非理想特性的引入會影響極化散射矩陣的測量,并可能導致目標散射特性和結構信息的解譯錯誤。本節利用所建立的仿真平臺就極化通道的非理想特性對極化散射信息提取的影響進行EM仿真。發射波形采用所設計的正交CCS同時極化波形,假設已使用文獻[23]中描述的方法進行了系統校準,但是殘余的通道非理想特性仍然存在。進一步假定互易系統在收發通道上有相同的非理想特性,殘余的通道非理想特性影響針對以下三種情況下進行回波仿真：(1) 相位不平衡為Δφ=0°時,幅度不平衡從0到5dB變化;(2) 幅度不平衡為0 dB時, 相位不平衡arg{f1}=arg{f1}=Δφ從0°到180°變化;(3) 幅度不平衡為0 dB,相位不平衡Δφ=0°時,雷達系統串擾δi,i=1～4從-10 dB～-30 dB變化。圖8給出了不同非理想特性條件下CCS同時極化ISAR成像后Pauli分解[1]的結果,其圖像具有紅色R=|SHH-SVV|、綠色G=|SHV+SVH|和藍色B=|SHH+SVV|顏色編碼。

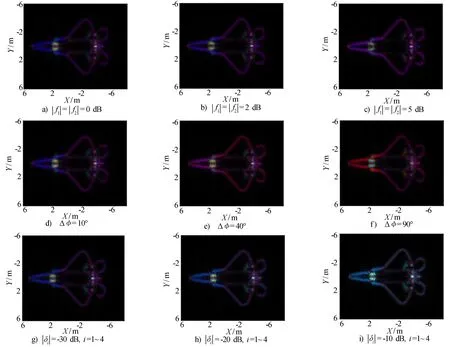
圖8 極化通道非理想特性下Pauli分解結果

圖8a)～圖8c)為幅度不平衡特性的影響,可以發現Pauli分解結果對雷達系統的幅度不平衡有較高的容忍性,2 dB范圍內的幅度不平衡幾乎不影響Pauli分解結果;機頭、座艙邊緣表現為藍色的一次散射機制,而較薄的水平機翼導致HH通道中的一次散射比VV通道中更強,類似于奇次散射和偶次散射的組合呈紫色。進氣孔為腔體形式散射機制復雜,等效相位中心發生偏離,呈現綠色的體散射形式。每種顏色的色調實際上表示了每種散射機制的能量貢獻。圖8d)～圖8f) 展現了極化通道相位不平衡特性的影響,10°范圍內的相位不平衡幾乎不影響Pauli分解結果;當收發通道的相位不平衡達到90°時,藍色的一次散射機制被解譯為紅色的二次散射機制。圖8g)～圖8i) 展現了極化通道串擾的影響,可發現-30 dB以下的極化串擾幾乎不影響Pauli分解結果;當極化串擾達到-10 dB時,目標散射機制發生很大的變化,會有多種散射機制的疊加,對目標極化信息的解譯產生很大的影響。

4 結束語