土石壩滲透分析方法綜述

何義江，戴長雷，*，孔維健，張一丁

(1.黑龍江大學 水利電力學院，哈爾濱 150080；2.黑龍江大學寒區地下水研究所，黑龍江 哈爾濱 150080)

土石壩因其獨特的工程建造特點而在水利工程建設中被廣泛應用，在2013年，由于黑龍江省氣候異常，發生罕見的特大洪水，致使黑龍江干流多處堤防工程的水位超過警戒線，其中八岔段就發生了嚴重的潰壩事故，致使下游大量良田被淹沒，造成嚴重經濟損失[1]。因此，對滲流問題的研究是預防潰壩等重大安全事故的重要舉措。滲流是指流體在多孔介質中流動的一種物理現象。由于各種土體或巖層具有不同的物理特性和機理，不同土體中水的運動狀況都不相同。由于重力或壓力作用，流體在地表以下土壤或巖層孔隙中流動的過程稱為滲透運動[2]，早在1852—1855年間，法國工程師達西進行大量試驗得出了達西定律，該定律奠定了滲流場的基本理論。滲透試驗是研究地表以下流體在土層中的水理特性以及研究流體運動情況的重要試驗[3]，所以，對滲流問題進行分析時，滲流區域的水頭和地下水分布特征、滲流量的計算、滲流對建筑地基的受力、滲流的速度分布，以及滲流引起的土工構筑物的變形等都是滲流研究中需要解決的問題。由于滲流的復雜性，目前滲透試驗的研究方法主要分為理論方法和模型試驗方法，理論方法有水力學法、有限元法和解析法等，試驗方法有電模擬和水力網模型等[4]。本文介紹滲流計算的三種方法，即水力學法、有限元法和水電比擬法，分別對三種方法進行計算原理梳理和優缺點分析，為土壩進行滲流試驗方法的選擇提供一定的參考。

1 水力學法

水力學法求解的基礎是將滲流區域內的滲流條件進行簡化。水力學法是一種解析法，能得出水頭、滲透流量的解析式，進而得出在流場中所求點的水頭或斷面流量。利用水力學法可以對浸潤線的確定、滲流量、滲流坡降以及水流流速等進行近似計算[5]。

1.1 計算原理

應用水力學法時需要采用連續介質和理想液體基本假設[6]，既假設滲透系數K在同一性質土樣中保持各向同性和壩體內部的水流為漸變流且通過任意過水斷面的平均流速和比降保持相等[7]。在運用水力學法進行土石壩滲流分析時，關鍵點其一在于能夠依據壩身結構、滲流特性以及壩身填筑材料將壩體進行分段，解析成簡單的幾何形狀分開進行數值計算，其二是依據流體通過上下游斷面的滲流總量相等原理建立各個幾何段之間的滲流連續關系。在計算滲流量時，當滲透系數相差5倍以內時，可將該土層視為同一種土層，代替土層的厚度可由滲流量不變的原則進行加權平均計算確定。在對不透水地基的土石壩進行滲流計算時，應將整個壩體分為上游和下游，并分別計算[8]。由于上游傾斜壩坡的滲流計算要比垂直入滲復雜，因此，可將上游的三角滲流段用等效的矩形代替，如圖1所示，其等效矩形的寬度可由式(1)進行計算：

(1)

式中：b為等效矩形寬度，m；m1為上游邊坡系數；H1為上游水深，m。

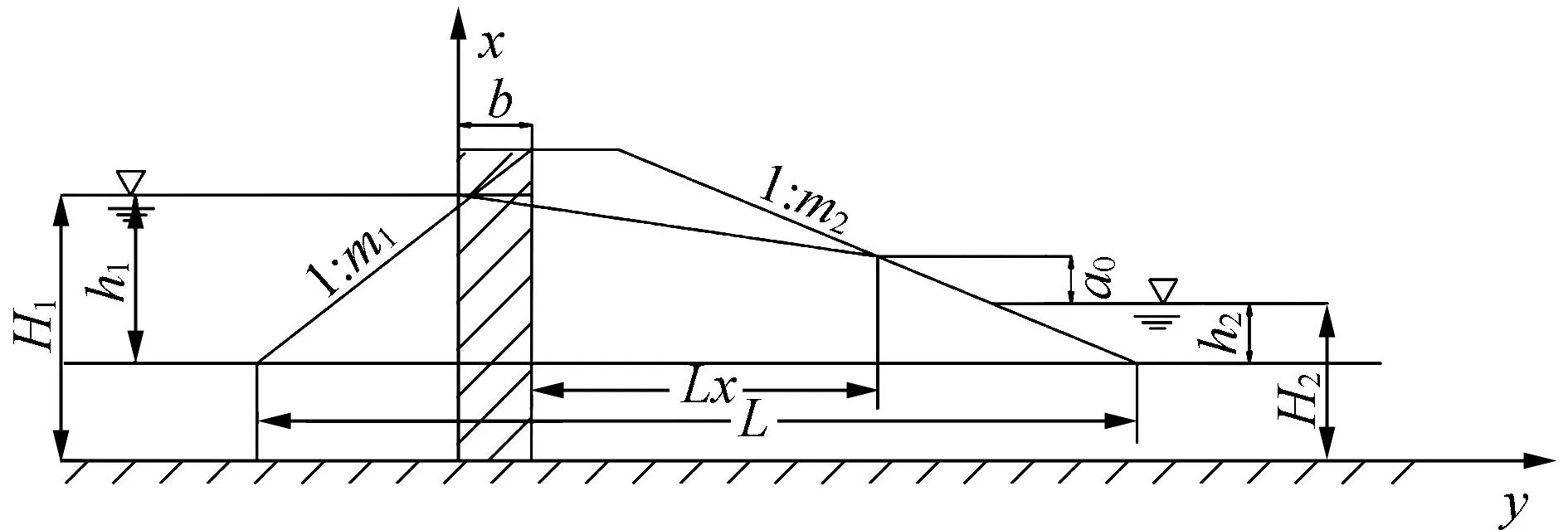
圖1 土體壩基的簡化

根據式(2)即可求出上游三角段和壩身中間段合成段的滲流量。

(2)

式中：q1為合成段的滲流量，m3；H2為下游水深，m；Lx為等效矩形到下游壩坡逸出點的水平距離，m；k為壩體和壩基平均滲透系數；a0為下游壩坡逸出點與下游水面距離，m。

下游段三角部分的滲流量可以分為水面以上和水面以下兩部分進行計算，根據達西定律其滲流量如式(3)：

(3)

式中：q2為下游逸出點滲流量，m3；m2為下游邊坡系數；L為上游壩底下游壩底截面寬度，m；q為該土石壩滲流量，m3。

根據連續條件q=q1=q2，如式(4)。聯立式(2)、式(3)和式(4)即可求出下游逸出點和該土石壩的滲流量，浸潤線方程便可根據式(5)相應求出。

(4)

(5)

式中：y為壩體浸潤線橫坐標；x為壩體浸潤線縱坐標。

若該壩型位于透水基層中，由于壩體和壩基滲透系數不同，則需要按照不同滲透系數對滲流量和浸潤線進行計算。

1.2 優缺點分析

在運用水力學法解決滲流問題時，前提是需要對壩體滲流條件進行一系列簡化，假定流體充滿整個土壤中孔隙部分，既將滲流場看成是一個連續體，就可用高等數學來分析研究滲流問題。該方法具有計算簡單且適用范圍廣等特點，能夠解決工程實際中大多數滲流問題。運用水力學法研究滲流問題往往借助滲流模型，滲流模型不需要考慮滲流在土壤中的具體滲流路徑，只需要考慮主要的滲流方向，但是其不足之處在于其求解出的滲流要素是僅為截面的平均滲流要素，無法求出流場內任一點的滲流要素，且該法在計算時進行的基本假設與實際存在差距，故求解結果往往會出現誤差[9]。

2 有限元法

20世紀40年代初，德裔美國數學家Richard Courant首次提出有限元方法。在處理復雜問題時，將連續求解區域分解成若干子區域，對子區域進行求解進而推廣到整個區域的求解，即為有限元[10]，這些有限元通過有限個節點能夠組合成一個等效的集合體，各有限元的連接方法和形狀不同，有限元法能通過數值模擬求解非標準幾何。假設每個子區域都有適當的逼近解，并由此得到該子區域整體滿足條件的解[11]。有限元法的基本原理是把微分方程及其邊界條件的求解轉換為泛函求極值的問題，其核心原理主要分為兩部分，分別為分塊插值和剖分離散[12]。有限元法是目前對于邊坡穩定性分析的一種常用的數值方法。

用有限元對土壩進行滲流分析的軟件有很多，例如AUTOBank-slop、GeoStudio中Seep/W和ANSYS等相關軟件。李保民[12]基于Seep/W對山東某土石壩進行滲流分析，探究了不同水位對壩體的滲流影響，進而對大壩的防滲加固提出建議。關萬彬[13]基于二維有限元法利用AUTOBank滲流分析有限軟件對西泉眼水庫土壩進行滲流分析，通過準確計算浸潤線和滲流狀態得出一些該壩的水理參數，進而對大壩的安全評估以及相關水利工程建設提供設計依據。陳雨瑤等[14]通過對黑龍江干流潰口八岔段采用GeoStudio軟件的Seep/W模塊進行滲流模擬，研究不同水位下堤防能否完成擋水任務。趙俊宇[15]在學位論文中通過Seep/W模塊研究非穩定滲流狀態下壩體滲流場的變化，得出水庫水位反復變化的速率不利于壩身的穩定性。

2.1 計算原理

有限元法是一種變分法與多項式通過插值結合的方法[16]，有限元法求解滲流問題時，是將滲流的基本微分方程和其邊界條件利用變分原理變換成函數的極值求解問題，在進行有限元分析的重要基礎理論是將一個連續域分解為若干個有限單元，建立插值函數的關系，將每個有限元通過節點連接[17](如圖2)，通過計算機對線性代數方程的形式進行求解，有限元計算時，其計算量往往比較大，因此，一般都要借助多種計算軟件，必要時還要編寫相應的計算程序。用有限元進行滲流分析的大致步驟如下[11]：

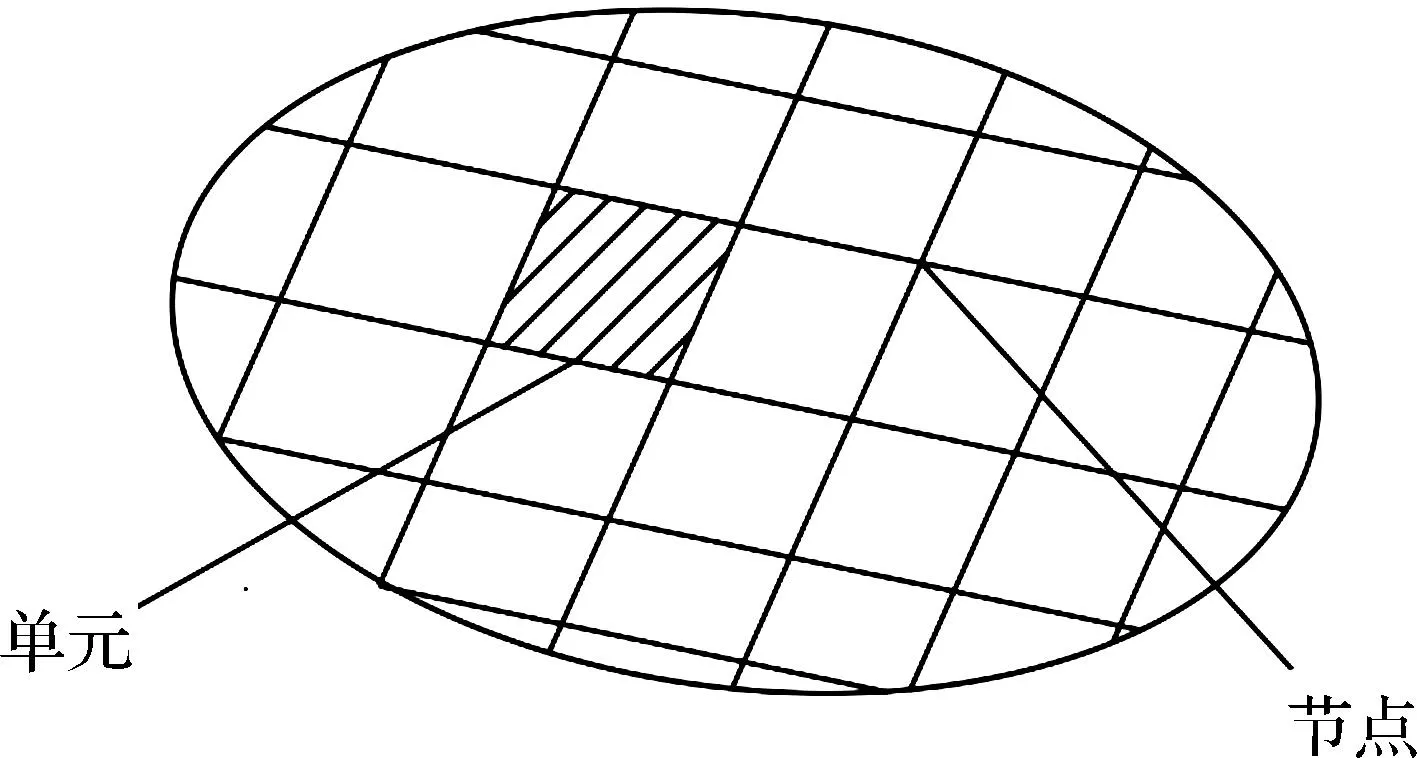
圖2 滲流區域劃分為若干個子區域

(1)把所研究的滲流區域分成若干個互相連接的單元。

(2)單元劃分后，按照單元建立水頭插值函數，分別確定每個單元的水頭函數。

(3)通過變分法推導有限單元方程，建立單元滲流矩陣。

(4)將各單元的單元矩陣集合形成整個滲流區的總的滲流矩陣。

(5)求出各節點的未知水頭值。

(6)由節點水頭值計算水力坡降和滲流量以及其他的水理參數。

2.2 GeoStudio中SEEP/W滲流模塊

SEEP/W是加拿大GEO-SLOPE公司GeoStudio系列軟件[18]，該軟件的主要目的是模擬地下水滲流分析。它是一種有限元軟件，用于分析土壤等多孔透水材料中的地下水滲流等水力試驗。該軟件在有限元的基礎上，能夠對土石壩體非飽和條件下孔隙水壓力進行分析，同時，還可用于分析邊坡在穩定狀態下的瞬態孔壓，在此基礎上，通過對孔隙內水壓力的時序分析，得到了滲流場、浸潤線、滲流流速、水力坡降等水理參數。在此基礎上，進一步研究邊坡和壩堤隨時間變化的穩定性。由于該模塊的強大的滲流計算功能，從而能夠分析不同工況條件下的滲流情況，得到較為清晰的計算結果，該軟件目前在水利工程建設以及礦產行業等其他領域中已被廣泛應用。

2.3 優缺點分析

有限元是近幾年出現的一類新的數值方法，它可以處理非均質、各向異性等復雜邊界條件，是目前國際上應用最為廣泛的一類滲流計算方法，它有很好的適應性和很高的精確度等特點，對于復雜地基上的大型水利樞紐工程，一般都會使用有限元法來解決滲透問題。采用有限元方法的優點在于它具有較強的計算靈活性(既可為離散空間，也可為基函數)。但有限元法是一種比較復雜的數值方法，雖然該方法可應用于不規則區域，但是對區域的連續性等要求比較嚴格，且計算工作量很大，必須依靠計算機輔助[19]。

3 水電比擬法

水電比擬法又稱水電模擬法，水電模擬試驗即通過研究電場中電流的運動來模擬地下水運動過程，從而研究滲流問題，我們稱之為水電比擬[20]，巴普洛夫斯基在1918年的首次提出了水電模擬，并在20世紀20年代將其用于土壤和大壩滲流問題研究[2]。該模型的理論依據是基于滲流方程和電學方程在數學表達式上具有相似性而建立相關性，利用電場模擬多種情況下的滲流場[21]。水電模擬試驗在水力學問題中應用比較普遍，是研究地下水運動的重要方法，不僅可以研究地下水滲流運動，還能研究地表水運動的問題。隨著水電模擬試驗技術的不斷發展，它已從解決單一介質中的流動問題擴展到了解決多層介質中的液體流動的問題，同時它也已經實現了從各向同性介質的問題到各向異性介質中的問題的過渡。還可以解決多維空間條件下的滲流問題。

對于穩定流，平面滲透流問題是測量電場中電荷的等勢線來比擬滲流場中的等水頭線，在此基礎上繪制流網研究滲流相關特性，對于無壓滲流，通過測定相對電位的比值來確定浸潤線，計算得到流網即可確定滲流區域的流場，進而場內的各種水理性質如孔隙水壓力、滲流流速、滲流坡降、滲流量等可相繼求得，依據這些水理性質便可以分析大壩的管涌現象、流沙現象等對工程安全構成威脅問題[22]。

3.1 計算原理

根據流體在孔隙介質中遵循達西定律，而流體在導電性介質中遵循歐姆定律，采用電仿真試驗來進行滲流問題的研究是水電模擬試驗的理論基礎。在穩定的滲流中，這兩個物理場可以用相同的數學方程，理論基礎是相似定理，在符合達西定律條件的背景下，滲流的運動規律與導體中的電流現象規律保持一致，其表現形式可以用Laplace方程來表示(具體對比關系見表1)，因此，在模擬有壓滲流電模型設計時，首先要滿足幾何形狀條件控制邊界條件的相似，以及考慮導電性質和滲透性質相似，將研究滲流場中的各種力學量轉化為研究電場中的各種電學量，進而將滲流問題轉換到電模型中，利用簡單的測試設備得到結果，再轉換為滲流區域。下表所列為滲流場和電場中各物理量的對比關系[23-24]。

表1 滲流場和電場各物理量對比關系

利用數學模型建立滲流場中達西定律與電場中歐姆定律的相似關系如式(6)、式(7)：

(6)

(7)

式中：負號表示水流沿水頭流動方向或者電位的降低方向。由以上二式可以發現，滲流場中與電場中各物理量一一對應關系如表1所示，將對應物理量用模型比尺表示，令λh=H/u，λk=k/ρ，λ=s/s′，λv=v/i，則式(7)可轉為式(8)：

(8)

將(8)式與(6)式和(7)式相比，欲使(8)式與(6)相等可得以下關系，如式(9)：

(9)

當模型比尺=1時，即如水工模型水力學相似律中模型與原型的弗勞德數比值或雷諾數比值=1。由式(9)可得，當模型電阻參數確定時，則只能改變電壓或電流密度，兩個變量確定一個，另一個變量也相繼確定。

由于滲流場和電場的介質參數具有相似性，在模擬均勻介質時，導電介質可以任選的前提是保證電導率和滲透系數保持固定比值，在模擬非均勻介質時，兩場中各層的對應參數應滿足以下關系，如式(10)：

(10)

式中：k1…kn為滲透系數；σ1…σn為導電率。

根據相似理論，若兩個數學模型相似必有相似解，這樣就可以在建立相似基礎上的模型裝置研究滲流問題，通過測定電場來求解相對復雜的滲流規律問題。

3.2 優缺點分析

利用水電模擬試驗研究滲流運動相較于其他模型試驗具有較強的優越性，例如在利用沙模型研究液體滲流時，沙子本身的粗細程度難以保障以及沙模內部滲流情況也難以捕捉，導致工作量很大。還有一種模型如黏性液體模型在做層流模擬試驗時，很難保證液體的黏度，并且模型邊界條件稍改變就會導致測量結果不精準。而電模擬在研究滲流問題時，所具有的優點可總結如下：

(1)該模型的設備較為簡單，使用電子儀表進行測試也較為方便，且測量精度較高。

(2)比較好控制邊界條件，可更好控制單一變量的改變。

(3)準確迅速，工作量較小。

(4)能夠更好地模擬壩體內滲流問題，仿真效果較好。

4 結 論

(1)在運用水力學法解決滲流問題時，其優點是通過構建水利模型計算結果比較符合工程實際，計算比較簡單，但是在計算時需要做出一些基本假定，且計算結果不是很精準，是一種近似解法。

(2)在用有限元進行分析滲流問題時，可以處理一些壩體邊界比較復雜的邊界條件，適應性較強，計算結果精度高，但是，這種方法的計算工作量很大，要借助計算機的幫助來實現。

(3)在進行水電模擬試驗來研究壩體滲流場問題時，試驗操作簡單，由于相似原理，能夠更好地模擬壩體內滲流問題，通過觀察電荷運行情況能更好地模擬壩體內液體滲流情況，其缺點是進行該試驗需要專門的設備，且調制設備過程較復雜，后期工作較多。