矩陣數據的分類預測方法
汪錢榮,陳文鈺,趙為華
(南通大學 數學與統計學院,江蘇 南通 226019)
0 引言
分類方法是統計學和數據科學的重要研究內容,分類的目的是通過給定的類別和訓練數據學會分類規則和構建分類器,進而用于未知數據的預測,其輸出結果是離散的類別值。如何應用數據挖掘方法對海量高維數據進行分析以發現潛在的數據模式,使得管理者能夠更加科學有效地進行決策,減小行動風險,已成為管理決策中的重要研究內容。在互聯網金融數據[1]、網絡電子消費數據、圖像與視頻數據[2]、醫療診斷與基因序列[3]分析中,數據經常以矩陣或高階張量形式呈現。使用矩陣或高階張量直接表達數據可以保留數據元素之間的結構信息[4],即數據相互間的內在關聯結構,且具有良好的計算特性和分析表達能力,特別是在高維度小樣本數據上尤為適用。本文關注矩陣數據的分類預測問題。
常用的分類方法有線性判別分析(LDA)、Logistic 回歸和支持向量機分類方法。線性判別分析最初是為了解決向量數據的特征提取問題,由Fisher在1936年開創性地提出了保證兩類樣本被有效識別的方法,通過最大化類間散點距離與類內散點距離的比值實現。通過假定不同類別數據服從具有不同數字特征的同一類分布,并引入數據的先驗知識建立分類規則,線性判別分析也可以很好地處理多分類數據;Logistic 回歸直接對分類的概率進行建模,根據回歸模型估計獲得分類決策函數;支持向量機基于最大距離間隔超平面進行建模,并基于二次凸優化方法獲得決策平面。然而已有的主要分類工作都是基于向量化方法進行的,當數據以矩陣(張量)呈現時,直接基于矩陣(張量數據)用向量化方法進行建模分析會導致擬合參數過多,出現過擬合現象,使估計精度和預測分析效果不佳等。
在處理多指標面板數據、衛星圖像數據、腦電信號圖像數據分析和分類問題時,數據自然地表示成三階張量或矩陣數據(灰度圖像),以往的工作絕大部分是先對數據進行向量化,然后應用判別分析方法進行分類預測[5—7]。將矩陣或張量數據向量化以后不僅破壞了原有數據之間的內在關聯性,而且使得參數的維數很大,特別是在假定向量化數據服從多元正態分布時,其協方差的參數個數特別多,會導致分類識別的準確率很低。隨著數據分析技術的進步和算法算力的提高,目前最流行的一種適用于矩陣數據的方法就是直接構建矩陣數據的分布模型。對于單個類別數據不均勻的情況,Viroli(2011)[8]將Hastie和Tibshirani(1996)[9]提出的混合判別分析模型拓展至矩陣正態分布,該模型基于觀測矩陣聚類,用于解決有監督和無監督的矩陣數據分類問題。Thompson 等(2020)[10]使用矩陣變量t 分布建模,并提出了一種期望最大化算法求解模型。然而在現實世界中,對于圖像等存儲結構性信息的矩陣數據,數據之間不僅具有相關性,而且經常表現出低秩特性。考慮數據之間的低秩特性有利于提高估計的精度和分類的準確率。
本文在矩陣正態分布假設下,結合矩陣的奇異值分解,引入目標矩陣的低秩估計方法,在有監督學習環境中解決分類問題。具體地說,本文通過奇異值的正則化來獲得矩陣低秩近似,通過最大化似然函數來探索數據樣本之間的關系,進而獲取模型的參數估計。將塊坐標下降法和增廣拉格朗日乘子法[11]相結合,提出了一種求解上述方法的聯合優化方案,并能自動獲得秩的估計。進一步結合線性判別分析方法,獲得矩陣數據下的判別規則。
1 矩陣正態分布
本文主要研究矩陣正態分布的自適應低秩估計方法及其在預測分類中的應用。向量可以看成張量的一維形式,矩陣是二階張量,三階以上的多維數組一般稱為張量。為具有擴展性,本文先給出張量正態分布的定義。
注意到上面定義的張量正態分布滿足cov[v ec(X)]=ΣJ?…?Σ1,此時稱隨機張量X∈?p1×…×pJ具有可分離的協方差結構。Kronecker可分性能夠大大減少估計協方差矩陣所需的自由度數量。例如,對于隨機張量X,如果vec(X)服從多元正態分布,那么協方差矩陣的自由度為;而如果vec(X)服從張量正態分布,那么協方差矩陣的自由度減少為
當J=2 時,隨機矩陣X∈?p1×p2服從矩陣正態分布,其密度函數為:
該分布記作Np1,p2(X,Σ1,Σ2)。此時,cov[v ec(X)]=Σ2?Σ1,為使得模型具有識別性,一般假定協方差陣(Σ1)11=1。
矩陣正態分布的統計推斷通常通過似然函數進行。假設有n個獨立的觀測數據,記參數為Θ={M,Σ1,Σ2},由式(1)可得到Θ的對數似然函數為:
求導后有如下的極大似然估計:
顯然上述協方差矩陣的極大似然估計沒有封閉解,Σ1和Σ2之間相互依賴,但可以基于任意正定矩陣(默認情況下使用單位矩陣)通過初始化相互交替迭代獲得估計。在很一般的正則條件下[14(]即對一些正常數C1、C2,滿 足,可以證明協方差估計的相合性:
可以證明均值估計的漸近正態性:
2 低秩分解及其模型的參數估計
假設矩陣數據Xi服從前文的矩陣正態分布,則Xi亦可寫成如下形式:
其中,Xi是p1×p2的觀測矩陣,M是待估計的p1×p2的真實矩陣,Ei是服從矩陣正態分布Np1,p2(0,Σ1,Σ2)的p1×p2隨機誤差矩陣。假設M有如下的奇異值分解:
其中,ur和vr均為單位正交向量,“?”表示向量之間的外積,w1>w2>…≥wmin{p1,p2}≥0 是一列取值下降的奇異值。為減少待估參數的個數進而提高預測推斷能力,假設M能被少數前R個奇異值分解表達,即:
本文將結合罰函數方法研究如何獲得低秩估計。對奇異值向量施加懲罰并通過選取合適的懲罰參數來縮減奇異值較小的值,進而自動獲得秩R的最優估計。令w=(w1,…,wR)T,基于上述討論,本文提出如下目標函數:
給定Σ1和Σ2,上式關于參數M的估計轉化為求解w、U、V的優化問題,目標函數如下:
為有效快速地求解式(3),本文基于塊坐標下降法獲得易于實施的估計算法。
本文使用交替更新方法依次更新ur、vr和wr。對ur,應用增廣拉格朗日乘子ADMM 算法可將約束問題式(4)轉化為無約束極小問題:
類似地,更新參數vr,其增廣拉格朗日函數為:
按照規則式(6)迭代更新上式參數和拉格朗日乘子直至收斂。
更新wr,式(4)中與參數wr有關的函數項為:
對上式求偏導并令偏導數等于零,可以得到:
本文引入軟閾值算法[15]來更新wr,令:
不斷交替迭代式(5)至式(7),直至達到預定的估計誤差精度(ε=10-5)時停止迭代,得到最終的估計。使用上述的罰函數方法能自動得到秩的估計,即=‖‖0,其中‖·‖0表示L0范數。上述模型的初始化和停止規則設置為:使用樣本均值初始化均值矩陣M,協方差矩陣Σ1、Σ2和矩陣U、V初始為單位陣,奇異向量w為全1向量。若滿足相對誤差,則ADMM算法終止。
由于模型的低秩結果依賴于正則化參數λ的選取,因此λ過大或是過小都會影響秩估計。本文基于貝葉斯信息準則(BIC,Bayesian Information Criterion)來進行模型選擇:
其中,lnL為對數似然函數值。最佳的正則化參數定義為=arg minλBIC(λ)。后文的數值模擬經驗表明BIC準則選擇效果很好。在一定的條件下,也可以證明秩選擇具有相合性,即P(=R0)→1。
注意到,式(2)中低秩表達在張量情形下就是張量的CP 分解[16],即對于一個J階張量X∈?p1×…×pJ,其CP 分解定義為:
利用上式,能很容易將本文提出的估計算法推廣至張量數據情形。本文不再贅述。
3 判別分析
判別分析是一種常用的分類方法。假設觀測值有K(K≥2)類,令πk表示一個隨機選擇的來自第k類的觀測值,即第k類的先驗,令fk(X)=P(X|y=k)表示來自第k類的觀測值的密度函數。由貝葉斯公式可以得到X屬于第k類的后驗概率pk(X)=P(y=k|X)。令lkj表示將第j類樣本誤分為第k類樣本的損失,基于后驗概率可以得到將樣本分類為第k類的期望損失(即條件風險),貝葉斯判定準則要求最小化條件風險。在0-1 損失的前提下,Rk(X)=1-pk(X),于是,最小化誤分類概率的貝葉斯分類器將X分配給后驗概率最高的類:
通常取對數運算arg maxklnpk(X)=arg maxkln πk fk(X)。值得注意的是,如果πk=1/K,那么極大化后驗分布式就等價于極大化似然函數。
本文假定不同類別數據服從具有不同的均值和相同協方差的矩陣正態分布,貝葉斯決策規則將X分派給第k組,其中:
特別地,當考慮二分類問題時,可以得到兩個類別的決策平面方程為:
當式(9)>0 時,將之判別為第二類;否則判別成第一類。實踐中,基于訓練樣本使用提出的方法可估計得出式(8)和式(9)中的參數。假設Dk為訓練樣本D中第k類樣本組成的集合,n為樣本總數,nk表示第k類樣本的個數,那么參數Mk的極大似然估計可以通過式(3)在集合Dk上求解,參數Σ1和Σ2的極大似然估計分別為:
4 模擬研究
本文通過大量的數值模擬來驗證低秩模型的有效性。模擬數據由以下模型生成:
其中:每個分量ur∈?p1、vr∈?p2互相獨立,每個元素先從標準正態分布中產生,然后進行正交化;wr是從1到100 內進行隨機抽樣的值,設真實的秩R=5;Ei是隨機誤差矩陣,Ei~Np1,p2(0,Σ1,Σ2)。
4.1 數值模擬1
對于矩陣Xi的維度,考慮三種情形:(Ⅰ)(p1,p2)=(8,10);(Ⅱ)(p1,p2)=(20,15) ;(Ⅲ)(p1,p2)=(30,20) 。設定協方差陣Σi(i=1,2)為滿足非對角元素為0.2 的標準的復合對稱協方差陣。
為衡量模型估計的精確性,本文使用均方根誤差(Root Mean Square Error,RMSE)來衡量估計值與真值之間的偏差:
本文報告樣本容量分別為n=100,200,300時100次模擬的平均結果,結果見表1。可以看出,在同一變量維數下,隨著樣本容量的增加,RMSE越來越小,說明參數的估計精度隨樣本量的增加不斷提高;隨著變量維數的增加,增大樣本容量依然有不俗的表現。對于矩陣的秩估計,本文統計了100 次模擬中正確估計的概率,在不同樣本容量、不同矩陣規格下模型均能準確識別秩。在生成樣本數據的同時,生成相同容量的獨立同分布的數據以供測試使用,表2 報告了低秩模型的預測能力,即比較擬合的均值矩陣與測試數據之間的誤差,并將其與非低秩模型進行對比。結果表明,本文所提低秩模型的預測精度更高,模型在高維情況下仍然保持穩定的預測精度。
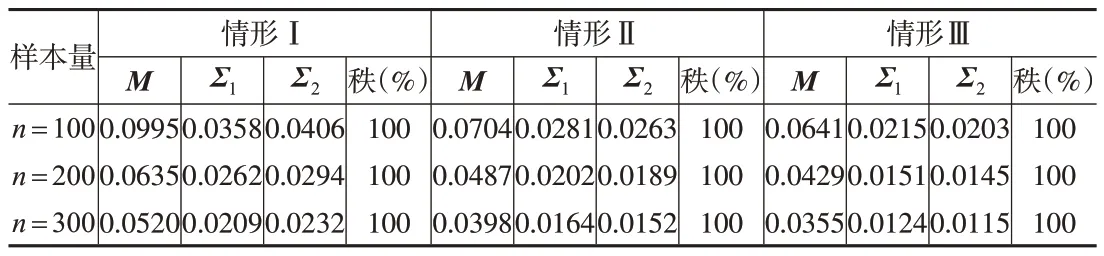
表1 模擬1中參數估計的RMSE和秩選擇的正確率
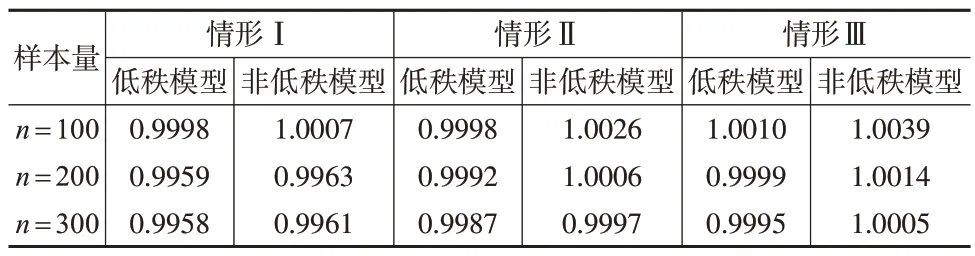
表2 模擬1中測試集RMSE預測情況
4.2 數值模擬2
以二分類問題為例,隨機生成A、B兩類數據,分別服從矩陣正態分布Np1,p2(MA,Σ1A,Σ2A)和Np1,p2(MB,Σ1B,Σ2B),協方差陣的設置與前文類似。同樣地,考慮三種不同維數情 形:(Ⅰ)(p1,p2)=(8,10);(Ⅱ)(p1,p2)=(20,15) ;(Ⅲ)(p1,p2)=(30,20)。
為衡量分類模型準確性,本文報告兩個重要指標:誤分類率和綜合評價指標F-Score。誤分類率表示錯誤分類的樣本比例。F-Score 是精確率(Precision)和召回率(Recall)的加權調和平均,精確率是針對預測結果而言的,表示在所有被預測為A(或B)類的樣本中實際為A(或B)類樣本的概率;召回率則是針對原樣本而言的,表示在實際為A(或B)類的樣本被預測為A(或B)類樣本的概率。F-Score定義為:
選取α=1 時的F1值,當F1較高時說明模型性能較好。
下頁表3報告了線性判別分析的相關分類情況,考察了兩類樣本容量分別為n=100,200,300 時的分類性能,對應各自類別生成了50個獨立同分布的測試數據進行驗證。將CP 低秩分解模型與非低秩模型和Logistic 回歸模型進行對比,結果表明,低秩模型能夠降低誤分類率,并且分類性能隨著樣本量的增加而提高,因為在所有的模型設置中,當樣本量n增加時分類錯誤率降低。兩類數據低秩模型的F1值均大于其他模型,這說明低秩模型是有效的。同時,本文所提的方法明顯優于使用Logistic 回歸模型的分類預測方法。
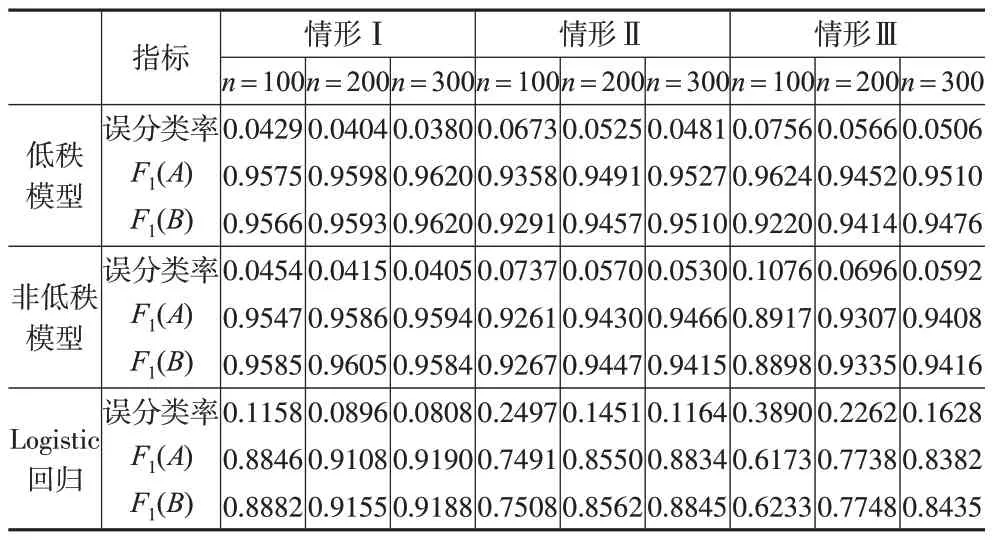
表3 模擬2中分類預測情況
5 實例分析
本文將低秩模型作為判別分析的工具用于兩個實際問題中。
5.1 陸地資源衛星數據
土地利用規劃是與當今人類生產和發展休戚與共的熱點問題,研究土地利用的動態變化,例如城鎮建設用地變化、耕地利用情況、草原保護和草地資源可持續利用狀況等具有重要意義。土地利用現狀檢測主要運用GIS、遙感及現代科學技術,掌握土地的利用及變化情況,可以為各級政府決策提供準確及時的土地數據。其中,陸地資源衛星影像數據是土地利用調查中最常用的數據,而采用遙感技術的多光譜衛星圖像允許在一個空間網格上進行多次觀測,從而產生了矩陣觀測值。
本文數據集來自UCI機器學習存儲庫主頁,原始陸地資源衛星數據是由澳大利亞遙感中心從美國宇航局購買的數據生成的。該數據集由不同光譜波段的4 幅相同場景的數字圖像組成,其中兩個在可見區域(對應于可見光譜中的綠色和紅色區域),兩個在(近)紅外區域。衛星圖像數據由3×3 平方鄰域表示,數據集的每一行包含該3×3 區域內每9 個像素在4個光譜波段中的像素值,以及一個代碼數字(表示中心像素的分類標簽)。本文選擇具有較高相似性的兩個類別:潮濕的灰土(代碼4)和帶植被茬的土壤(代碼5)的圖像。UCI 網站提供了包括訓練集(415、470)和測試集(211、237)的數據案例。本文對數據集進行預處理,將每行數據構建為一個維數為4×9 的矩陣。先驗概率為訓練集中各類別所占的比例,利用R軟件包MixMatrix 將類別建模為矩陣正態分布進行分類,其誤分類率為0.1004。本文考慮低秩假定的矩陣正態分布模型,得到的誤分類率為0.0893,施加復合對稱協方差結構得到的誤分類率降低至0.0670,此時估計的矩陣秩為2。本文進一步分析了兩個分類器具體的預測結果(見表4),低秩模型對于兩類土地類型的識別性能均有提高。同時,本文繪制了ROC 曲線(見圖1),可以明顯看出,曲線面積接近于1,說明分類器具有較強的識別能力,且考慮低秩的分類能力更優良。
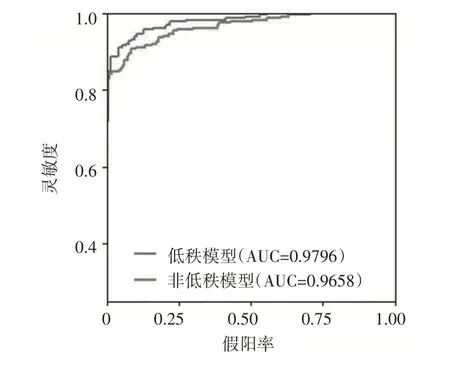
圖1 衛星圖像數據的ROC曲線
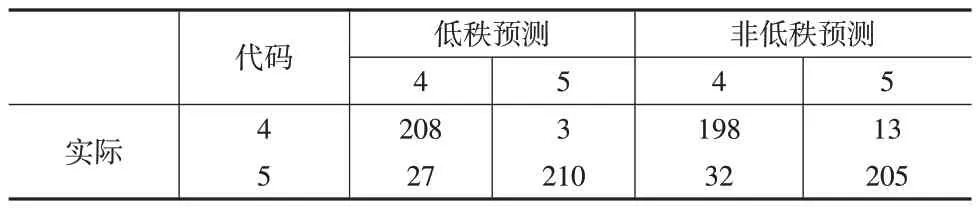
表4 衛星圖像數據分類結果
5.2 手寫數字識別
該數據集由意大利布雷西亞的Tactile 公司(http://www.tattile.it)創建,并于1994 年捐贈給意大利羅馬塞梅恩傳播科學研究中心(http://www.semeion.it)用于機器學習研究。該數據集掃描了大約80 人的1593 個手寫數字,將其放在一個16×16 的矩形框中,灰度值為256;然后使用固定閾值將每個圖像的每個像素縮放為布爾(1/0)值。要求每個人在紙上寫下0到9的所有數字并寫兩次,第一次以正常的方式寫下數字(確保精確性),第二次則快速寫下數字(沒有精確度)。考慮到3、5 和8 具有較高的相似度,本文的目標是從測試集中識別出這3 個數字。對數據進行預處理,使用16×16 大小的矩陣存儲每個手寫數字數據,得到共473 例(其中數字3 和5 均有159例,數字8 有155 例)數據。由于數據集未劃分訓練集和測試集,故采用5 折交叉驗證法劃分數據集:每次選取4個子樣本作為訓練集,1 個子樣本用作測試,共重復5 次實驗。將每個類的條件概率密度近似為一個矩陣正態分布,最小化訓練集中的誤分類率,表5 報告了平均結果,無論是從誤分類率還是從AUC 值來看,低秩模型分類效果均更好。下頁表6報告了5次實驗的秩估計結果,對于矩陣情形為16×16 的訓練數據,低秩模型使用較小的秩,獲取了手寫數字圖像的大部分信息,并在測試集上表現出不錯的分類性能。

表5 交叉驗證平均結果
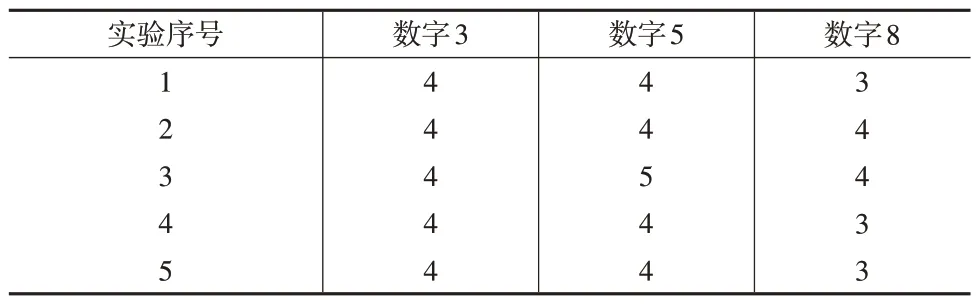
表6 秩估計結果
6 總結
本文主要研究了基于矩陣(張量)正態分布的低秩張量分解模型,給出了基于低秩分解方法的模型參數估計方法,并將其作為估計類概率密度的工具應用于判別分析中。模擬研究說明了低秩分解模型的有效性,在模擬的兩類數據下與非低秩模型和Logistic回歸模型進行了對比分析,實例數據分析進一步驗證了低秩模型在分類預測性能上表現更好。盡管本文是在矩陣數據情形下討論的估計算法,但是很容易將方法應用于張量數據的分類研究中。當數據中進一步含有協變量信息時,可以進一步研究矩陣回歸建模的低秩估計及其分類方法。此外,當數據中含有異常值時,可進一步研究基于矩陣或張量t分布的低秩估計及其分類和聚類方法[10,17]。

