以核心素養為導向 拓展探究型創新題

邴國良 銀英

2024年遼寧省中考數學樣卷的壓軸題（第23題）被調整為幾何綜合探究題，這與遼寧省各市歷年中考壓軸題相比變化較大.此題是幾何綜合題中拓展探究型的創新題，其設置體現了以核心素養為導向，由解題走向解決問題的數學學科考試測評方向，通過問題初探、類比分析、學以致用考查考生分析問題、解決問題的能力.

原題再現

【問題初探】

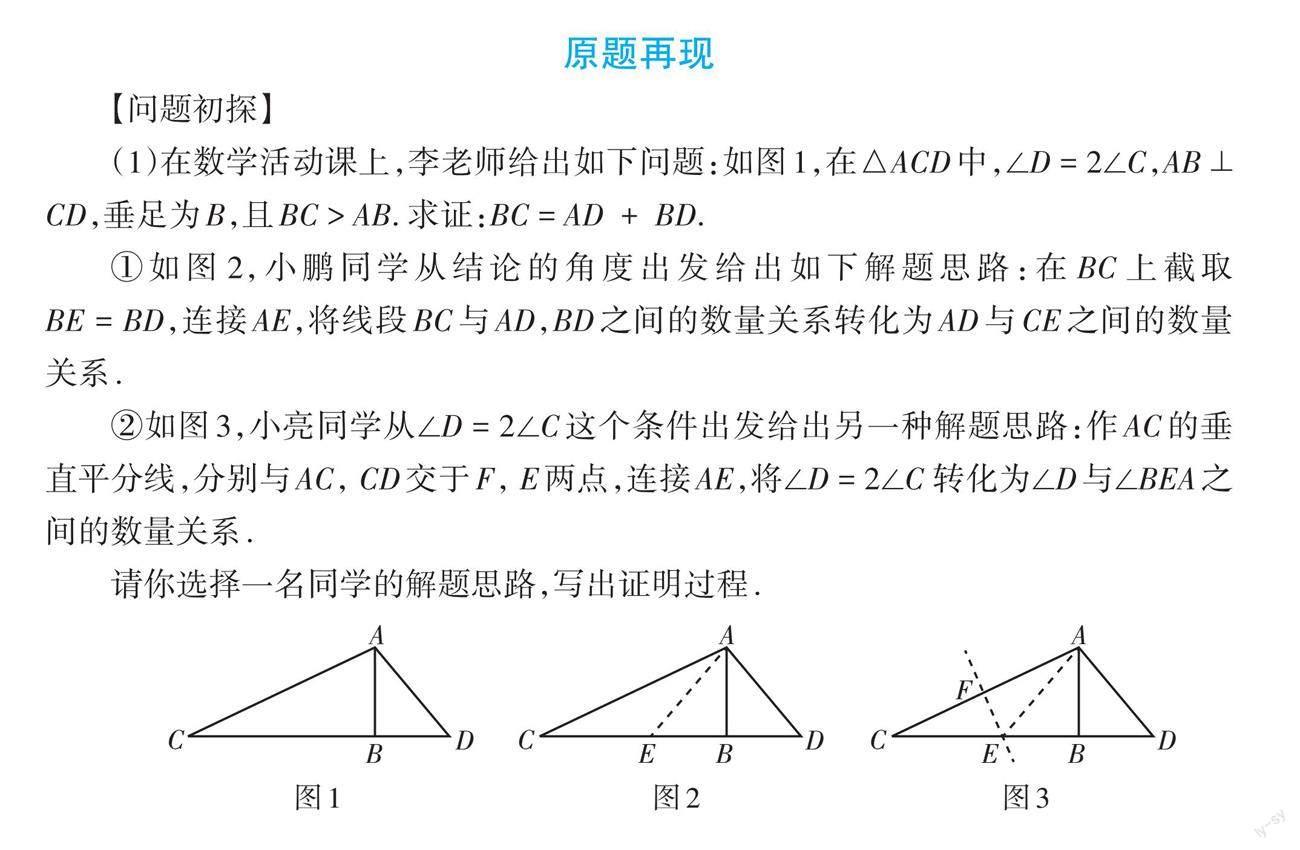
（1）在數學活動課上，李老師給出如下問題：如圖1，在△ACD中，∠D = 2∠C，AB ⊥ CD，垂足為B，且BC > AB. 求證：BC = AD ?+ ?BD.

①如圖2，小鵬同學從結論的角度出發給出如下解題思路：在BC上截取[BE=BD]，連接AE，將線段BC與AD，BD之間的數量關系轉化為AD與CE之間的數量關系.

②如圖3，小亮同學從∠D = 2∠C這個條件出發給出另一種解題思路：作AC的垂直平分線，分別與AC， CD交于F， E兩點，連接AE，將∠D = 2∠C 轉化為∠D與∠BEA之間的數量關系.

請你選擇一名同學的解題思路，寫出證明過程.

【類比分析】

（2）李老師發現之前兩名同學都運用了轉化思想，將證明三條線段的關系轉化為證明兩條線段的關系. 為了幫助學生更好地感悟轉化思想，李老師將圖1進行變換并提出了下面問題，請你解答.

如圖4，在Rt△ABC中，∠ABC = 90° ，過點A作AD [?] BC（點D與點C在AB同側），若∠ADB = 2∠C. 求證： BC = AD + BD.

【學以致用】

（3）如圖5，在四邊形 ABCD中，[AD=1003]，[CD=1213]，[sinD=35]，[∠BCD=∠BAD]，∠ABC = 3∠ADC，求四邊形 ABCD 的面積.

破解策略

第（1）題：需具備的知識儲備有等腰三角形的性質、三角形外角的性質、垂直平分線的性質或三角形全等的判定.本小題相當于給出了部分范例，需要同學們補充詳細證明過程，也為后續的類比分析與學以致用提供了證明的主要轉化方向：一個是轉化線段之間的關系，另一個是轉化角度之間的關系（二倍角的轉化）.

方向1：線段轉化——截長補短

思路：如圖2，在BC上截取BE = BD，連接AE，可得AB所在直線為線段DE的垂直平分線，則AE = AD，可得∠D = ∠AEB. 由∠D = 2∠C，得∠AEB = 2∠C，進而可得∠C = ∠CAE，則CE = AE = AD，所以BC = AD + BD.

方向2：二倍角轉化——利用外角和等腰三角形轉化

思路：如圖3，作AC的垂直平分線，分別與AC，CD交于F，E兩點，連接AE，則AE = CE，易證∠BEA = 2∠C. 由∠D = 2∠C，得∠D = ∠BEA，則AE = AD，BE = BD，所以BC = AD + BD.

第（2）題：在第（1）題的基礎上增加了“AD [?] BC（點D與點C在AB同側）”而且“∠ADB = 2∠C”，考生需要思考：“添加的這兩個條件起什么作用？”進而思考：“通過怎樣的轉化會出現問題1中的基本圖形？”思考方向還是線段截長補短和二倍角轉化.

思路1：如圖6，在BC上截取BE = AD，連接AE，證[△ABE≌△BAD]，轉化為問題（1）.

思路2：如圖7，作AC的垂直平分線，交BC于點E，證[△ABE≌△BAD]，轉化為問題（1）.

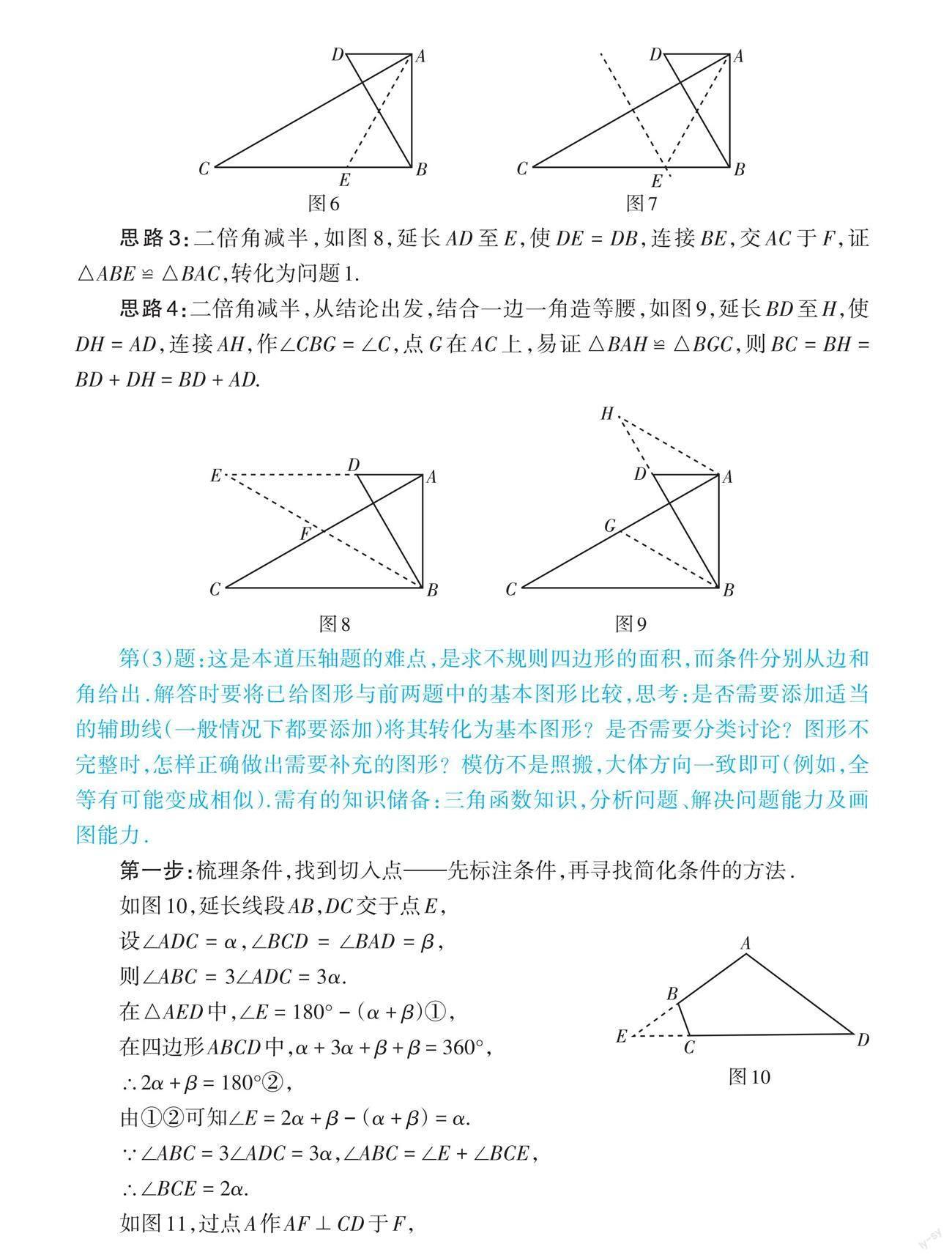
思路3：二倍角減半，如圖8，延長AD至E，使DE = DB，連接BE，交AC于F，證[△ABE≌△BAC]，轉化為問題1.

思路4：二倍角減半，從結論出發，結合一邊一角造等腰，如圖9，延長BD至H，使DH = AD，連接AH，作∠CBG = ∠C，點G在AC上，易證[△BAH≌△BGC]，則BC = BH = BD + DH = BD + AD.

第（3）題：這是本道壓軸題的難點，是求不規則四邊形的面積，而條件分別從邊和角給出.解答時要將已給圖形與前兩題中的基本圖形比較，思考：是否需要添加適當的輔助線（一般情況下都要添加）將其轉化為基本圖形？是否需要分類討論？圖形不完整時，怎樣正確做出需要補充的圖形？模仿不是照搬，大體方向一致即可（例如，全等有可能變成相似）.需有的知識儲備：三角函數知識，分析問題、解決問題能力及畫圖能力.

第一步：梳理條件，找到切入點——先標注條件，再尋找簡化條件的方法.

如圖10，延長線段AB，DC交于點E，

設∠ADC = α，[∠BCD=∠BAD] = β，

則∠ABC = 3∠ADC = 3α.

在△AED中，∠E = 180° - （α + β）①，

在四邊形ABCD中，α + 3α + β + β = 360°，

∴2α + β = 180°②，

由①②可知∠E = 2α + β - （α + β） = α.

∵∠ABC = 3∠ADC = 3α，∠ABC = ∠E + ∠BCE，

∴∠BCE = 2α.

如圖11，過點A作[AF⊥CD]于F，

在△AFD中，由[sin D=35]，可得AF = 20，EF = FD = [803]，CF = [413]，CE = 13.

至此，同學們會發現四邊形ABCD的面積等于△AED的面積與△BEC的面積之差.解決問題的關鍵是求△BEC的面積.

第二步：回歸基本圖形，應用已證結論快速求解.

如圖12，作BH ⊥ CE于點H，由前面已知CE = 13，△BEC為第（1）題中已證模型，可得EH = BC + HC，設BH = 3x，BE = 5x，EH = 4x，則HC = 13 - 4x，BC = 8x - 13.

在△BHC中，由勾股定理可得（[3x]）2 + （13 - 4[x]）2 = （8[x] - 13）2，解得x = [10439]，所以BH = 3x = [10413]，∴四邊形ABCD 的面積 = [12·DE·AF-12·CE·BH=12×1603×20-12×13×10413=14443].

拓展延伸

（1）問題情境：如圖13，正方形ABCD中，AB = 6，點E為射線BC上一動點，將△ABE沿AE所在直線翻折，得到△AFE，延長EF，射線EF與射線CD交于點G，連接AG．

①當點E在線段BC上時，求證：DG = FG；

②當CE = 3時，則CG的長為_______.

（2）思維深化：在△ABC中∠BAC = 45°，AD為BC邊上的高，且BD = [2] + 1，CD = [2] - 1，請直接寫出AD的長．

答案：（1）①略；②4或[365]. （2）AD的長為[2+3]或[1].

（作者單位：沈陽市南昌初級中學，沈陽理工大學附屬學校）