異步電機矢量控制系統Simulink 建模與教學仿真

姚愛芬，張澤軒，陳劍美，姜麗媛，國騰飛

（滄州交通學院 電子與電氣工程學院，河北黃驊，061199）

0 引言

隨著電力電子半導體器件的發展，靜止式變頻器的應運而生，異步電機在速度可調電機拖動中逐漸得到廣泛的應用[1]。基于動態數學模型的異步電動機具有非線性、強耦合、多變量的特點[2]，面對大量的數學公式，復雜的模型結構，學生學習起來比較困難，如何使學生高效學習異步電機控制方法，如何能把課堂上復雜的知識簡單化，使上課效率進一步提高，成為我們要迫切需要解決的關鍵問題。

本文在分析交流異步電機矢量控制的基礎上，借助MATLAB仿真軟件，提出了易于教學用的異步電機仿真模型，配合課本知識講解，把復雜的公式轉化成仿真模型，將課本所學控制方法運用于實際的控制系統中，便于學生更好地理解異步電機控制。異步電機矢量控制的基本思想就是仿照直流控制系統一樣[2~3]，采用經典的雙閉環控制，外環速度環采用比例積分控制，電流環采用電流滯環控制，搭建基于MATLAB 的異步電機間接矢量控制系統的仿真模型，并將異步電機轉差頻率控制和矢量控制系統的仿真模型結果進行對比，驗證了搭建模型的正確性，同時將搭建的仿真模型應用到課堂教學中，反過來又增加了學生學習的興趣性，更有利于對異步電機控制方法的理解。

1 矢量控制原理

1.1 模型建立

異步電動機調速系統分析既可以基于穩態模型分析也可以基于動態模型分析。由于異步電動機非線性、強耦合、多變量的性質[2]，必須從其動態模型出發去建立其高性能動態模型。

為了獲得和直流電機相似的控制模型，按照產生相同磁動勢的原則，可以在三相繞組與兩相繞組，以及兩相繞組與兩相繞組間進行變換。通過3s/2r 變換，可以將三相坐標系下電壓、電流變換到兩相坐標系下，如公式(1)所示，這樣兩相旋轉坐標系繞組就可以等效于靜止坐標下的三相繞組。

依照磁動勢相同的原則，可以完成兩相坐標系下電壓、電流到三相坐標系的轉換，如公式(2)所示，簡稱為其逆變換。

1.2 異步電動機磁鏈檢測

交流異步電動機的磁場控制是調速控制的關鍵，異步電動機的勵磁回路是非獨立的，定子繞組輸入的電流包括轉矩分量和勵磁分量兩部分，給異步電機控制帶來了很大困難。因此對磁場進行定向需要實時監測磁場，即采用磁鏈模型進行觀測。

（1）二相靜止坐標系下的轉子磁鏈模型

兩相靜止坐標系下異步電動機電壓方程為：

在兩相靜止坐標系下，轉子磁鏈分量為：

得到轉子電流分量為：

在方程(3)中令轉子電壓在α、β軸的分量為0，帶入到轉子電流方程式中，得到轉子電流磁鏈方程為：

上式中p為微分算子，Tr=Lr Rr，為轉子回路的時間常數。

（2）二相旋轉坐標系下的轉子磁鏈電流模型

同樣可以建立二相旋轉坐標系下的轉子磁鏈電流模型，該模型是按照轉子磁鏈進行定向的。通過檢測電動機的轉速rω和定子三相電流進行計算得到轉子磁鏈，定子電流勵磁分量ism和轉矩分量ist是定子三相電流經3r/2s 變換得到的[17]。異步電機矢量控制方程為公式(7)、(8)、(9)。

上式中，np為電動機極對數，ωs為轉差角頻率。轉差角頻率ωs和轉子角頻率ωr組成定子角頻率ω1，即ω1=ωs+ωr。

如此可以保持轉子磁鏈指標值恒定，則轉矩則直接利用電流的轉矩分量等指標來對其進行控制。同理，ωs也能夠在這一時期借助ist計算，轉子磁鏈ψr則必須利用勵磁分量ism等來開展計算。轉矩分量ist由轉速PI 調節器ASR 得到，并計算得到ωs的數值，同樣因為轉子磁通量保持不變，因而有pψr= 0。

1.3 矢量控制原理

為了保證對轉子磁鏈的控制，本文采用磁鏈的閉環控制。控制電路采用典型的雙閉環控制策略，轉速調節器ASR 構成外環的調節，內環增加了轉矩調節器和磁鏈調節器，構成帶轉矩內環的轉速、磁鏈閉環矢量控制系統[5]，原理如圖1 所示。主電路采用電流源型逆變器，控制電路包括了電流變換和磁鏈觀測環節、坐標變換和逆變器控制等環節[6]。

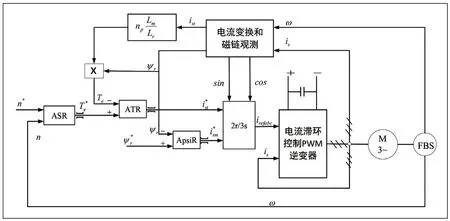
圖1 帶轉矩內環的轉速、磁鏈閉環異步電動機的矢量控制圖

轉速的給定信號與反饋信號的差值送入轉速調節器，其輸出又作為轉矩調節器的給定信號，ATR 的輸出作為定子電流的轉矩分量[7]。通過磁鏈觀測環節可以計算出磁鏈大小，作為磁通調節器ApsiR 的輸入，ApsiR 的輸出又作為定子電流的勵磁分量[8]。最后通過2r/3s 變換控制產生用于控制兩電平逆變器主電路的脈沖信號，最終實現對異步電機的控制。

2 仿真模型的搭建

2.1 仿真電路設計

2.1.1 電流滯環逆變器

本文選擇電流滯環控制器產生逆變器的驅動脈沖信號。滯環控制器由三個單相電流滯環控制器打包而成。由轉速給定經轉速調節器和轉矩調節器得到轉矩給定電流ist＊，由磁鏈的給定經磁鏈調節器得到磁鏈的給定電流ism＊，ist＊和ism＊經2r/3s 轉化得到三相電流給定信號，與用多路測量儀檢測得到的異步電動機的三相電流，即反饋信號相比較，由滯環模塊Relay產生六路逆變器的驅動信號[9]，如圖2 所示。

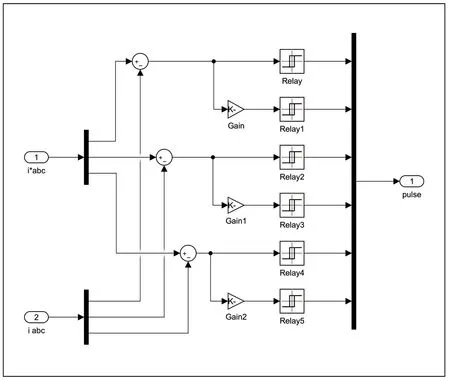
圖2 三相電流滯環控制變流器

2.1.2 轉子磁鏈電流模型

電流模型采用如圖3 所示的兩相同步旋轉坐標系下的，按轉子磁鏈定向的磁鏈電流模型[10]。通過從電動機測量模塊得到的定子三相電流（iabc），經abc 三相坐標軸到dq 軸的轉換得到定子電流的磁鏈分量ism 和轉矩分量ist，磁鏈分量ism 經計算得到輸出轉子磁鏈（psir）；磁鏈分量和定子電流轉矩分量經計算得到轉差ws，轉差ws 和轉子角頻率wr 組成定子角頻率w1，經積分得到三相定子電流的相角（wt）。

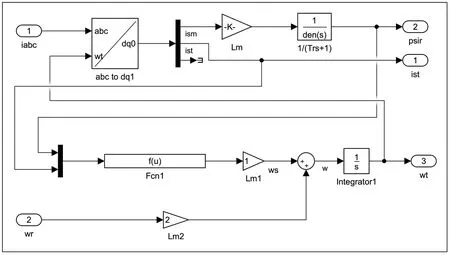
圖3 轉子磁鏈電流模型

2.1.3 仿真模型搭建

將仿真模型中所用的轉速、磁鏈和轉矩調節器都設計成帶限幅輸出的PI 控制方式，如圖4 所示。

圖4 PI 調節器模型

電動機采用標幺值模型，逆變器采用全控型IGBT 組成的三相橋式模塊，電流滯環逆變器采用如圖2 所示模型，轉子磁鏈電流模型采用如圖3 所示模型，三個調節器模型如圖4 所示，構成如圖5 所示異步電機矢量控制系統仿真模型。

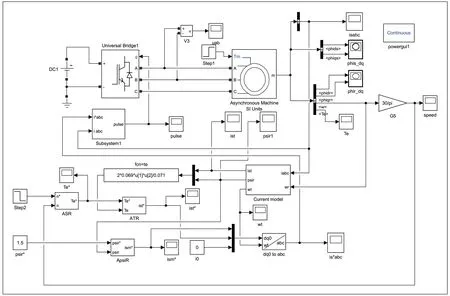
圖5 異步電機矢量控制系統仿真模型

2.2 仿真參數設置

仿真模型用電機參數為：380V、50Hz，二對極，Rs=0.435?，Lls=0.002H，Rr=0.816?，Llr=0.002H，Lm=0.069H，J=0.19kg?m2；σ= 1-L2m(LsLr)=0.056，Tr=0.087。逆變器直流電源為510V。

矢量控制系統仿真模型參數如表1 所示。

表1 矢量控制系統仿真模型參數

3 仿真結果分析

設置電機參數，初始狀態下，負載轉矩和轉速假設如下：初始時把電機轉速假定為1420r/min，負載轉矩為0，即系統空載啟動；0.4s 時把負載轉矩階躍突變為80N.m 保持不變，轉速不變；0.6s 時將給定轉速降低為1000r/min，轉矩大小不變，分析系統的啟動性能和抗負載擾動能力。

圖6 所示虛線為磁鏈閉環控制下電機轉速，實線為轉差頻率控制下電機轉速，黑色虛線是給定轉速的大小。由圖可以看出，磁鏈閉環控制和轉差頻率控制下電機都可以實現對給定轉速的跟蹤控制。轉差頻率控制下電機轉速上升較快，但是不夠平滑；磁鏈閉環矢量控制下，啟動階段轉速上升更為平滑；突加負載后轉速有所下降，但是下降很小，說明設計系統抗負載擾動能力較強；0.6s 時轉速降為1000r/min，兩種控制系統都能夠跟隨轉速變化很快穩定下來，達到設定的轉速，但是磁鏈閉環控制下，轉速動態速降較小，轉速變化更快，恢復時間較短，證明所設計系統的穩定性。

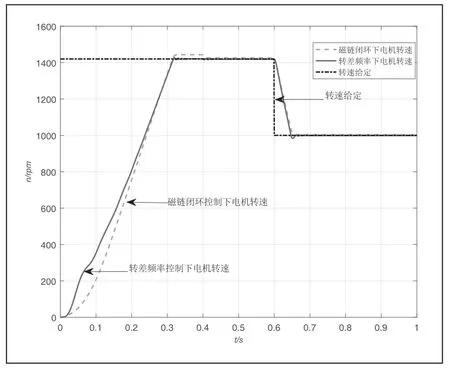
圖6 電機轉速曲線

圖7 所示為帶轉矩內環的轉速、磁鏈閉環控制下電機電磁轉矩變化曲線。由于磁鏈閉環，電磁轉矩會隨著磁鏈的增加而增加；0.13s 后轉矩達到最大值，電機以恒轉矩在升速；0.32s 時轉速達到給定轉速，電磁轉矩下降至0；0.4s 時突加負載給定，電磁轉矩開始上升，與負載轉矩相平衡，直至電機達到新的穩態。0.6s 時轉速降為1000r/min，電磁轉矩迅速下降變負，電機進行減速，當轉速穩定為1000r/min 時，轉矩又迅速上升為與負載轉矩相平衡。此時，電機經過短暫的過程，在新的轉速下又處于穩定運行狀態。

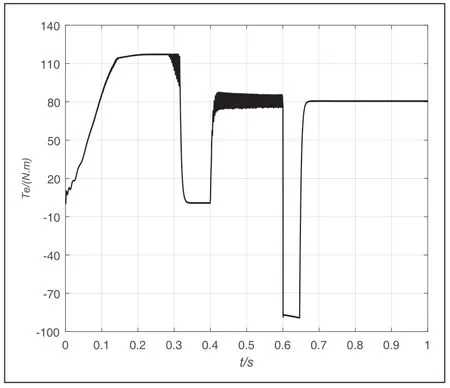
圖7 電磁轉矩波形

圖8 為電動機定子三相電流波形，初始狀態時定子電流隨電磁轉矩增大而增大，電磁轉矩上升到最大電磁轉矩時，定子電流開始減小，0.32s 時轉速達到給定轉速，電流減小到最小值；0.4s加載后，轉矩馬上突變，電流也相應增加；0.6s轉速下降后，定子電流隨著下降，最后趨于穩定，說明電動機能穩定運行。

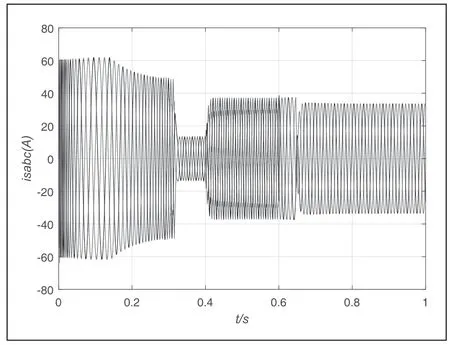
圖8 定子相電流波形

4 結論

本文主要分析了矢量控制系統，并通過對轉差頻率和矢量控制系統仿真結果對比可以得到，矢量控制下，磁鏈閉環可以保證電機啟動時啟動過程加快，實現準時間最優控制；動態抗擾性能良好，能夠穩定運行，說明了所設計模型的正確性。同時反哺課堂教學，增加學生對矢量控制思想的理解，理解解耦的思想，培養當代大學生對課本知識思考的能力和用所學知識解決生活中實際問題的能力。