具有保凸性的三點二重逼近細分格式

王 燕，李志明

(1.合肥師范學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院，安徽 合肥 230601；2.合肥工業(yè)大學(xué) 計算機與信息學(xué)院，安徽 合肥 230009)

0 引言

細分曲線曲面作為一種重要的曲線曲面造型的方法，因其簡單、易操作，一直是學(xué)者研究的重點[1-17]。比較經(jīng)典細分格式的有Dyn[2]提出的四點二重插值細分格式，Weissman[3]提出的六點二重插值細分格式，Hassan等[4-5]提出的三重插值細分格式，包括三點三重和四點三重兩類，Chaikin[6]提出的割角細分格式。后來的學(xué)者在這些經(jīng)典細分格式的基礎(chǔ)上，又提出了很多新的細分格式，并且研究了這些細分格式的性質(zhì)，比如Siddiqi[7]提出了一類具有C2連續(xù)性的三點二重細分格式；黃樹培等[8]提出了一類三點二重插值細分格式，并研究了其保凸性、分形的性質(zhì)。在上述研究的基礎(chǔ)上，本研究提出了一種三點二重逼近細分格式，這種格式是非對稱的，證明了它具有C1連續(xù)性，并給出了它具有保凸性的參數(shù)取值范圍，最后通過實例證明了這種格式的有效性。

1 預(yù)備知識

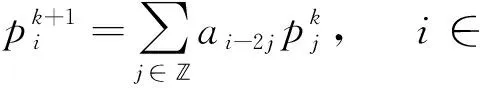
(1)

為二重細分格式，其中a={ai}i∈是相對應(yīng)的細分格式的Mask(掩模)。

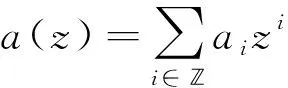
定理1[9]若二重細分格式S一致收斂，則其Maska={ai}i∈必須滿足

(2)

定理2[9]若二重細分格式S的掩模a={ai}i∈滿足(2)式，則必存在一個二重細分格dPk=S1dPk-1成立，其中一般地，將Sn記為S的n階差分格式，為其掩膜，則為Sn的生成多項式。

定理3[9]若二重細分格式S的掩模a={ai}i∈及其j階差分格式Sj(j=1，2，…，n)的掩模滿足

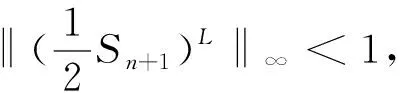
2 三點二重細分格式

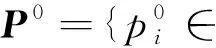
(3)

當(dāng)μ=0時，格式(3)變?yōu)槿蜝樣條細分格式：

定理4對于任意給定的初始控制多邊形，當(dāng)參數(shù)-3/16 <μ<5/16 時，由式(3)得到的極限曲線具有一致收斂性。

證明細分格式(3)的生成多項式為

a(z)=(1/8 +μ)z-2+(1/2 +μ)z-1+(3/4 -2μ)+(1/2 -2μ)z+(1/8 +μ)z2+μz3，

由定理2可得S1的生成多項式為

a(1)(z)=2za(z)/(1+z)=(1/4+2μ)z-1+3/4+(3/4-4μ)z+1/4z2+2μz3，

則

當(dāng)-3/16<μ<5/16時，

‖1/2S1‖∞=1/2 max{|1/4 +2μ|+|3/4 -4μ|+|2μ|，3/4 + 1/4}<1，

由定理3可知，細分格式(3)生成的極限曲線是一致收斂的。

定理5對于任意給定的初始控制多邊形，當(dāng)參數(shù)-1/8 <μ< 1/4時，由式(3)得到的極限曲線的連續(xù)性是C1連續(xù)。當(dāng)參數(shù)μ=0時，格式(3)得到的極限曲線具有C2連續(xù)性。

證明由定理2可得S2的生成多項式為

a(2)(z)=2za(1)(z)/(1+z)=(1/2+4μ)+(1-4μ)z+(1/2-4μ)z2+4μz3，

則

當(dāng)-1/8 <μ< 1/4時，

‖1/2S2‖∞=1/2max{|1/2+4μ|+|1/2-4μ|，|1-4μ|+|4μ|}<1。

根據(jù)定理3，細分格式(3)得到的極限曲線具有C1連續(xù)性。

當(dāng)μ=0時，

a(3)(z)=z+z2，‖1/2S3‖∞= 1/2 max{1，1}<1，

根據(jù)定理3，由細分格式(3)得到的極限曲線具有C2連續(xù)性。顯然，細分格式(3)變?yōu)槿蜝樣條細分格式。

3 保凸性

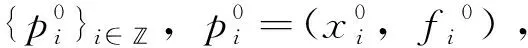
證明由細分格式(3)得

(4)

(5)

假設(shè)對某些k≥0，k∈，i∈成立，則當(dāng)0≤μ≤1/8時，根據(jù)式(4)和式且則，i∈成立。定理6證畢。

因此當(dāng)參數(shù)0≤μ≤1/8時，在給定的初始凸頂點下，由細分格式(3)得到了具有C1連續(xù)性的保凸曲線。

4 數(shù)值分析

文獻[7]中給出的細分格式的系數(shù)是固定的、對稱的細分格式，文獻[8]中給出了一類插值型的三點二重細分格式，連續(xù)性最高達到C1連續(xù)。本文提出的三點二重細分格式是非對稱的，并且?guī)螤顓?shù)，具有可調(diào)節(jié)性，連續(xù)性最高是C2連續(xù)，與已有的三點二重細分格式的比較結(jié)果列于表1。

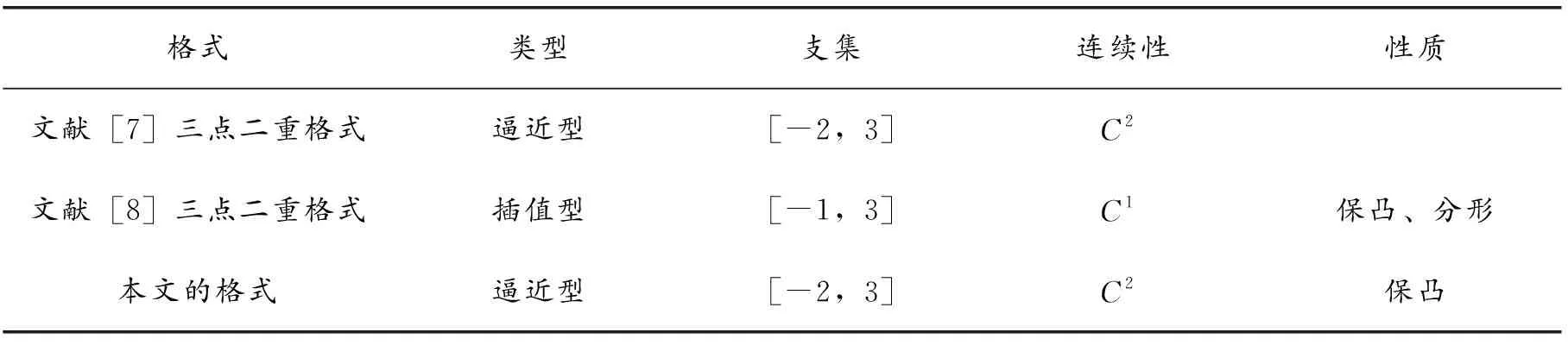
表1 與已有三點二重格式的比較

對于相同的控制多邊形，當(dāng)參數(shù)μ取不同值時，可以得到不同的造型曲線，見圖1和圖2。由圖1、2可見，參數(shù)μ的引入增加了造型的靈活性。

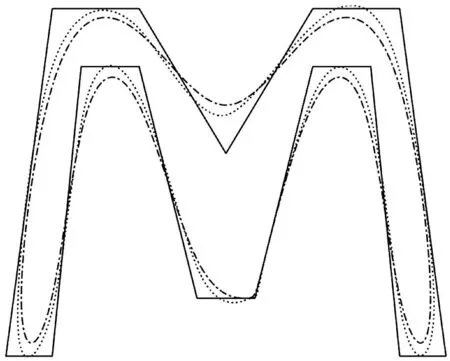
圖1 由格式(3)生成的極限曲線(虛線為μ=-1/32，點劃線為μ=0)

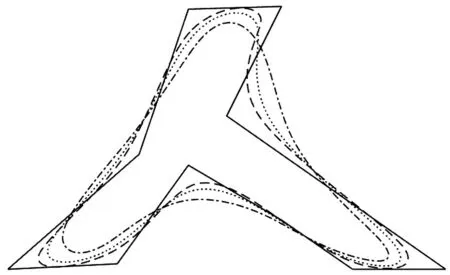
圖2 由格式(3)生成的極限曲線(雙劃線為μ=-1/32，虛線為μ=0，點劃線為

當(dāng)參數(shù)0≤μ≤1/8時，由格式(3)可以生成具有保凸性的極限曲線，見圖3，若初始給定的控制頂點是凸的，則由格式(3)生成的極限曲線也是凸的。

圖3 由格式(3)生成的保凸曲線(μ=1/10)

5 結(jié)論

本文研究了一類新的三點二重逼近細分格式，給出了其不同的連續(xù)性對應(yīng)的參數(shù)區(qū)間，這種格式的支集是[-2，3]，是非對稱的，且?guī)螤顓?shù)，具有可調(diào)節(jié)性，連續(xù)性最高是C2連續(xù)，當(dāng)參數(shù)在[0，1/8]取值時，生成的極限曲線具有保凸性，可以較好的用于工業(yè)設(shè)計。下一步，我們將繼續(xù)研究該格式的其他性質(zhì)，并嘗試推廣到曲面細分格式。