基于改進(jìn)PSO-BP 模型的鐘差預(yù)報(bào)研究

張穎博 ,劉音華,* ,劉婭

(1.中國科學(xué)院國家授時(shí)中心,西安 710600;2.中國科學(xué)院大學(xué),北京 101408)

0 引言

精確的鐘差預(yù)報(bào)可以運(yùn)用在實(shí)時(shí)動(dòng)態(tài)精密單點(diǎn)定位、衛(wèi)星自主導(dǎo)航以及接收機(jī)自主完好性檢測(cè)等方面[1]。在時(shí)間尺度的計(jì)算,為時(shí)間保持提供實(shí)時(shí)駕馭參考也很重要[2]。此外,鐘差預(yù)報(bào)在時(shí)間測(cè)量、時(shí)間比對(duì)等方面可以與實(shí)測(cè)的鐘差數(shù)據(jù)形成對(duì)照,度量測(cè)量的鐘差精確性等領(lǐng)域都具有十分重要的意義[3]。

比較成熟的鐘差預(yù)報(bào)模型有多項(xiàng)式QP 模型、灰色GM(1,1)模型、時(shí)間序列模型:典型的有ARMA 模型、神經(jīng)網(wǎng)絡(luò)模型等[4]。QP 模型形式簡(jiǎn)單,但是容易受到噪聲和鐘差中的周期項(xiàng)影響,精度難以進(jìn)一步提升[5]。GM(1,1)模型的灰微分方程與擬合的微分方程難以完全一致,影響模型的預(yù)報(bào)精度[6]。ARMA 模型的計(jì)算方法比較繁瑣,對(duì)非平穩(wěn)序列預(yù)報(bào)精度低[7]。傳統(tǒng)的神經(jīng)網(wǎng)絡(luò)由于結(jié)構(gòu)簡(jiǎn)單、具有較強(qiáng)的非線性映射能力,在非線性擬合,預(yù)測(cè)數(shù)據(jù)等方面應(yīng)用十分廣泛[8]。

鐘差信號(hào)存在著頻率源的不穩(wěn)定性和多種噪聲,鐘差由趨勢(shì)項(xiàng)(頻率偏差產(chǎn)生)和非平穩(wěn)項(xiàng)(各類噪聲產(chǎn)生)組成[9]。而BP 模型則是利用非線性基函數(shù)實(shí)現(xiàn)從輸入到輸出的非線性映射,可以通過訓(xùn)練來接近任何非線性函數(shù)[10]。網(wǎng)絡(luò)沿著誤差減小最快方向通過反向計(jì)算對(duì)權(quán)值和閾值進(jìn)行調(diào)整,隨著訓(xùn)練的進(jìn)行,最終的誤差會(huì)逐漸減小。但是采用BP 模型預(yù)報(bào)鐘差過程中,初始權(quán)值和閾值為隨機(jī)值,經(jīng)過訓(xùn)練可能陷入局部極值,即局部最優(yōu)解,錯(cuò)失全局極值點(diǎn),造成網(wǎng)絡(luò)訓(xùn)練結(jié)果具有偶然性,導(dǎo)致鐘差預(yù)報(bào)結(jié)果有較大的不穩(wěn)定性。

針對(duì)這一問題,利用粒子群優(yōu)化(PSO)BP 神經(jīng)網(wǎng)絡(luò)的算法來提高鐘差預(yù)報(bào)的穩(wěn)定性和精確性。然而標(biāo)準(zhǔn)的粒子群算法也有陷入局部極值、后期收斂慢的問題[11]。因此需要改進(jìn)粒子群優(yōu)化算法中重要參數(shù)的生成方法,然后進(jìn)行迭代計(jì)算BP 神經(jīng)網(wǎng)絡(luò)最優(yōu)的初始權(quán)值和閾值。經(jīng)過試驗(yàn)分析,改進(jìn)后的PSO-BP 算法可以進(jìn)一步提高鐘差預(yù)報(bào)精度。

1 改進(jìn)的粒子群優(yōu)化算法

對(duì)粒子群優(yōu)化算法中的三個(gè)重要參數(shù)的生成方法進(jìn)行改進(jìn)。從原本固定不變的值,優(yōu)化為隨著迭代不斷更新的值。

1.1 粒子群優(yōu)化算法

粒子群優(yōu)化算法中的粒子通過群內(nèi)相互學(xué)習(xí)、信息傳遞以及個(gè)體積累自身尋優(yōu)的經(jīng)驗(yàn),聚成一個(gè)群體,并且朝著目標(biāo)——最優(yōu)位置前進(jìn),粒子通過個(gè)體最優(yōu)和群體最優(yōu)兩個(gè)位置向量更新自身的位置[12,13]。用適應(yīng)度函數(shù)來度量每次迭代運(yùn)算時(shí)粒子得到的最優(yōu)位置。

求解方法如下:假設(shè)群體有s個(gè)粒子,每個(gè)粒子是D維向量,其中第i個(gè)粒子(i=1,2,…,s)的位置向量記為Xi=(xi1,xi2,…,xiD),粒子i每次迭代的最優(yōu)位置為Pi=(pi1,pi2,…,piD),所有粒子每次迭代的最優(yōu)位置為Pg=(pg1,pg2,…,pgD),粒子i的速度為Vi=(vi1,vi2,…,viD)。粒子i的第d維位置更新如式(1)和式(2)所示。

式中:k——迭代次數(shù);d——粒子i的維數(shù),取值1,2,…,D;ω——慣性權(quán)值;c1——個(gè)體學(xué)習(xí)因子;r1,r2——隨機(jī)值;c2——群體因子;α——速度的權(quán)重。

此外,防止粒子盲目搜索,將vid限制在(-vmax,vmax);xid限制在(-xmax,xmax)。

1.2 參數(shù)改進(jìn)的粒子群優(yōu)化算法

ω越大,粒子速度在相鄰兩次迭代計(jì)算時(shí)幅度變化越大,越有利于全局尋優(yōu);反之ω值越小,對(duì)于局部尋優(yōu)更有利[14]。為了平衡算法中全局尋優(yōu)和局部尋優(yōu)的能力,對(duì)PSO 算法中ω采用非線性遞減生成方法,原理如式(3)所示

式中:k——當(dāng)前迭代次數(shù);ωmax——慣性權(quán)重的最大值,一般取0.9;ωmin——最小值,一般取0.4;K——總的迭代次數(shù)。

隨著運(yùn)算的進(jìn)行,ω非線性遞減。開始迭代尋優(yōu)時(shí),適應(yīng)度較大,說明距離最優(yōu)解較遠(yuǎn),此時(shí)需要較大的ω值使算法具有較強(qiáng)的面向全局尋找最優(yōu)解的能力;隨著迭代的進(jìn)行,選較小的ω值更有利于算法在局部尋找最優(yōu)解。

同時(shí)對(duì)PSO 算法中的學(xué)習(xí)因子通過非對(duì)稱線性變化的參數(shù)生成方法進(jìn)行改進(jìn)。在初始尋優(yōu)時(shí),把c1設(shè)置較大、c2設(shè)置較小來擴(kuò)大搜索范圍。隨著迭代的進(jìn)行,c1線性遞減,c2線性遞增,在全局最優(yōu)位置上逐漸收斂粒子。原理如式(4)和式(5)所示

2 改進(jìn)的鐘差預(yù)報(bào)PSO-BP 模型

BP 模型原理參考文獻(xiàn)[15],不再詳細(xì)敘述。改進(jìn)參數(shù)生成方法的PSO-BP 模型預(yù)報(bào)鐘差過程分為以下幾個(gè)步驟:

1)鐘差數(shù)據(jù)的預(yù)處理:首先將鐘差數(shù)據(jù)進(jìn)行一次差分消除趨勢(shì)項(xiàng),通過絕對(duì)中位差法(MAD)對(duì)異常值進(jìn)行剔除并修正。對(duì)差分?jǐn)?shù)據(jù)進(jìn)行歸一化處理,目的是統(tǒng)一數(shù)據(jù)范圍,提高模型訓(xùn)練過程中的穩(wěn)定性,并且加快模型訓(xùn)練的速度。

2)劃分包括輸入數(shù)據(jù)和輸出數(shù)據(jù)在內(nèi)的鐘差數(shù)據(jù)的訓(xùn)練集和測(cè)試集:劃分L組每組M維的數(shù)據(jù)作為輸入,記作T=(t(1),t(2)t(L));同時(shí)有L組每組J維的衛(wèi)星鐘差數(shù)據(jù)作為輸出Yf=(y(1),y(2)y(L))。M維輸入和J維輸出對(duì)應(yīng),將L組數(shù)據(jù)中的P組數(shù)據(jù)作為訓(xùn)練集,T組作為測(cè)試集。

3)改進(jìn)的PSO 算法實(shí)現(xiàn)步驟如下:

①確定神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu):設(shè)計(jì)的BP 模型輸入層、隱含層、輸出層神經(jīng)元個(gè)數(shù)M、I、J分別為4、9、1;隱含層層數(shù)為1。

②PSO 算法初始化:輸入到隱含的權(quán)值ωmi,共4 ×9 個(gè);輸入到隱含的閾值bi,共9 個(gè);隱含到輸出的權(quán)值ωij,共9 ×1 個(gè);隱含到輸出的閾值bj,共1個(gè)。隨機(jī)初始化55 維向量{ωmi,bi,ωij,bj}作為粒子的位置向量Xi;同理初始化55 維速度向量Vi;粒子群規(guī)模s設(shè)置為50;K設(shè)置為100;適應(yīng)度為訓(xùn)練后的BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)鐘差數(shù)據(jù)的均方誤差MSE:

式中:N——預(yù)報(bào)的歷元個(gè)數(shù);t(n)——實(shí)際鐘差;(n)——經(jīng)過訓(xùn)練后的網(wǎng)絡(luò)預(yù)測(cè)的鐘差。

③根據(jù)粒子的位置和鐘差訓(xùn)練集的輸入輸出數(shù)據(jù),得到適應(yīng)度值,更新粒子位置Pi和Pg。迭代完成時(shí),如果存儲(chǔ)的每次迭代的全局最優(yōu)適應(yīng)度收斂,則輸出最優(yōu)適應(yīng)度的粒子位置。

④將最優(yōu)的粒子位置向量劃分不同層之間的權(quán)值和閾值輸入到BP 神經(jīng)網(wǎng)絡(luò)作為初值。

4)BP 神經(jīng)網(wǎng)絡(luò)通過反向修正方法獲得最佳的網(wǎng)絡(luò)權(quán)值和閾值。用經(jīng)過訓(xùn)練的神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)鐘差數(shù)據(jù),具體過程如下:

①初始化網(wǎng)絡(luò)的參數(shù):訓(xùn)練次數(shù)、學(xué)習(xí)率和訓(xùn)練目標(biāo)。

②對(duì)處理好的訓(xùn)練集數(shù)據(jù)進(jìn)行訓(xùn)練,隱含層傳遞函數(shù)f選為Sigmoid 函數(shù)[10],網(wǎng)絡(luò)對(duì)訓(xùn)練集的第p組數(shù)據(jù)預(yù)測(cè)值Ya(p)為

③由網(wǎng)絡(luò)的實(shí)際輸出Ya與期望輸出Yf得到誤差E,當(dāng)誤差E未達(dá)到訓(xùn)練目標(biāo)時(shí),繼續(xù)進(jìn)行迭代,達(dá)到訓(xùn)練目標(biāo)時(shí)迭代完成。由測(cè)試集的輸入數(shù)據(jù)對(duì)鐘差數(shù)據(jù)進(jìn)行預(yù)測(cè),對(duì)預(yù)測(cè)數(shù)據(jù)反歸一化、反差分得到預(yù)測(cè)的原始鐘差,通過測(cè)試集的期望鐘差計(jì)算均方根誤差RMSE。模型預(yù)報(bào)鐘差流程如圖1 所示。

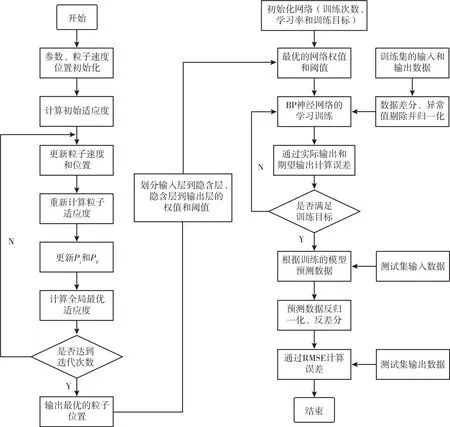
圖1 改進(jìn)的PSO-BP 模型鐘差預(yù)報(bào)流程圖Fig.1 Improved clock difference prediction flow chart of PSO-BP model

3 改進(jìn)的PSO-BP 模型的鐘差預(yù)報(bào)試驗(yàn)分析

采用IGS 提供的鐘差產(chǎn)品數(shù)據(jù)進(jìn)行試驗(yàn)分析,訓(xùn)練集數(shù)據(jù)時(shí)段最好選取整數(shù)倍的BDS 運(yùn)行周期。選取時(shí)間為2023 年2 月8 日0 時(shí)至9 日24 時(shí)的數(shù)據(jù),采樣間隔為5 min,共有576 個(gè)歷元的鐘差數(shù)據(jù)點(diǎn)。前288 個(gè)歷元的鐘差數(shù)據(jù)作為訓(xùn)練集,后288個(gè)歷元的鐘差數(shù)據(jù)作為測(cè)試集。

3.1 參數(shù)改進(jìn)前后PSO 算法對(duì)比試驗(yàn)

改進(jìn)的PSO 算法中的ω值以非線性遞減的方法生成,c1和c2值則以非對(duì)稱線性變化的方式生成。與ω取值為0.9、c1和c2取值為1.49445 的固定值的標(biāo)準(zhǔn)PSO 算法作對(duì)比。

把每一次PSO 算法迭代后的全局最優(yōu)適應(yīng)度值存儲(chǔ)在數(shù)組中,通過得到的適應(yīng)度最小值及相應(yīng)的迭代次數(shù)衡量改進(jìn)算法的有效性。選取PRN24、PRN30、PRN35 和PRN38 四顆衛(wèi)星,用前24 h 鐘差作為訓(xùn)練集數(shù)據(jù)輸入到PSO 算法中進(jìn)行迭代尋找最優(yōu)適應(yīng)度值。PSO 算法對(duì)四顆衛(wèi)星鐘差迭代過程中全局最優(yōu)適應(yīng)度值變化曲線如圖2 所示。

圖2 PSO 參數(shù)優(yōu)化前后全局最優(yōu)適應(yīng)度值變化Fig.2 Global optimal fitness changes before and after PSO parameter optimization

從圖2 中可以大致看出,PSO 算法優(yōu)化前,雖然迭代前期收斂較快,但在最終得到的全局最優(yōu)適應(yīng)度并不是最小值,也就是陷入局部的最優(yōu)解。參數(shù)改進(jìn)后的PSO 算法得到最終的適應(yīng)度值較改進(jìn)前變小,搜索精度更高,后期搜索收斂速度加快。參數(shù)優(yōu)化前后對(duì)四顆衛(wèi)星鐘差預(yù)報(bào)過程中最終迭代得到的全局最優(yōu)適應(yīng)度值的統(tǒng)計(jì)表如表1 所示。

表1 全局最優(yōu)適應(yīng)度對(duì)比統(tǒng)計(jì)表Tab.1 Global optimal fitness comparison table

從表1 中可以看出,經(jīng)過參數(shù)優(yōu)化后的PSO 算法,得到全局最優(yōu)適應(yīng)度值的迭代次數(shù)較優(yōu)化前減少較多。并且適應(yīng)度更小,粒子位置更佳。所以對(duì)PSO 算法中的參數(shù)生成方法改進(jìn)后,在搜索極值時(shí)的速度和精度有所改善。

3.2 改進(jìn)的PSO-BP 模型和BP 模型鐘差預(yù)報(bào)對(duì)比試驗(yàn)

通過PRN24、PRN26、PRN35、PRN38 四顆衛(wèi)星鐘差預(yù)報(bào)結(jié)果對(duì)比BP 模型和改進(jìn)的PSO-BP 模型的鐘差預(yù)報(bào)性能。兩種模型采用相同結(jié)構(gòu)的神經(jīng)網(wǎng)絡(luò),不同的是初始權(quán)值和閾值:改進(jìn)的PSO-BP 模型使用迭代尋優(yōu)的結(jié)果,而BP 模型采用隨機(jī)數(shù)。用前24 h 共288 個(gè)歷元數(shù)據(jù)作為訓(xùn)練集進(jìn)行建模,預(yù)報(bào)后24 h 的衛(wèi)星鐘差,分別進(jìn)行10 次獨(dú)立的預(yù)報(bào),用RMSE 衡量預(yù)報(bào)精度。BP 和PSO-BP 預(yù)報(bào)結(jié)果如圖3 所示。10 次預(yù)報(bào)結(jié)果的RMSE 值的統(tǒng)計(jì)結(jié)果:均值MEAN 和標(biāo)準(zhǔn)差STD 如表2 所示。

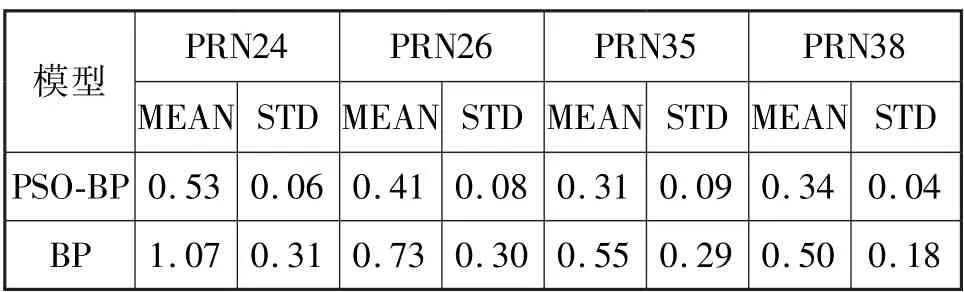
表2 10 次預(yù)報(bào)RMSE 統(tǒng)計(jì)表Tab.2 10 times forecast RMSE table 單位:ns

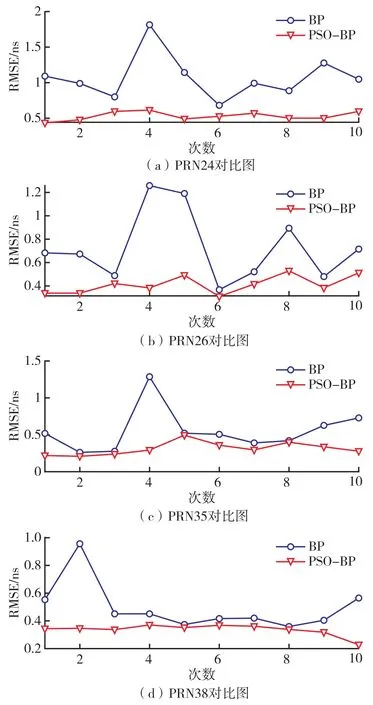
圖3 兩種模型十次鐘差預(yù)報(bào)的RMSE 值對(duì)比圖Fig.3 Comparison of RMSE for the 10 times clock difference forecast of the two models

由圖3 可以看出,BP 模型在針對(duì)同一組數(shù)據(jù)進(jìn)行多次試驗(yàn)后,由于初始權(quán)值和閾值為隨機(jī)值,因此很容易陷入局部最優(yōu),導(dǎo)致網(wǎng)絡(luò)預(yù)測(cè)數(shù)據(jù)的不穩(wěn)定,造成訓(xùn)練后的網(wǎng)絡(luò)不可重現(xiàn)。而經(jīng)過改進(jìn)的PSO-BP 模型,在預(yù)測(cè)鐘差數(shù)據(jù)時(shí)采用尋優(yōu)后的初始權(quán)值和閾值,盡管預(yù)測(cè)鐘差結(jié)果也有差異,但是波動(dòng)更小、更穩(wěn)定。由表2 計(jì)算可得,對(duì)于PRN24衛(wèi)星,10 組試驗(yàn)PSO-BP 模型預(yù)報(bào)數(shù)據(jù)的精度較BP模型提高了50.4%;穩(wěn)定性提高了80.6%。PRN26衛(wèi)星預(yù)報(bào)精度提高了43.8%;穩(wěn)定性提高了73.3%。PRN35 衛(wèi)星預(yù)報(bào)精度提高了43.6%;穩(wěn)定性提高了69%。PRN38 衛(wèi)星預(yù)報(bào)精度提高了32%;穩(wěn)定性提高了77.8%。

3.3 改進(jìn)的PSO-BP 模型和三種傳統(tǒng)模型鐘差預(yù)報(bào)對(duì)比試驗(yàn)

為了進(jìn)一步驗(yàn)證參數(shù)改進(jìn)的PSO-BP 模型鐘差預(yù)報(bào)的精度,對(duì)12 顆BDS 鐘差進(jìn)行預(yù)報(bào)并與三種傳統(tǒng)的鐘差預(yù)報(bào)模型:ARMA、QP 和GM(1,1)進(jìn)行對(duì)比分析。這里僅給出改進(jìn)的PSO-BP 模型與三種傳統(tǒng)模型對(duì)PRN26、PRN35、PRN38、PRN39 四顆衛(wèi)星在288 個(gè)歷元的預(yù)報(bào)結(jié)果,預(yù)報(bào)對(duì)比如圖4 所示。

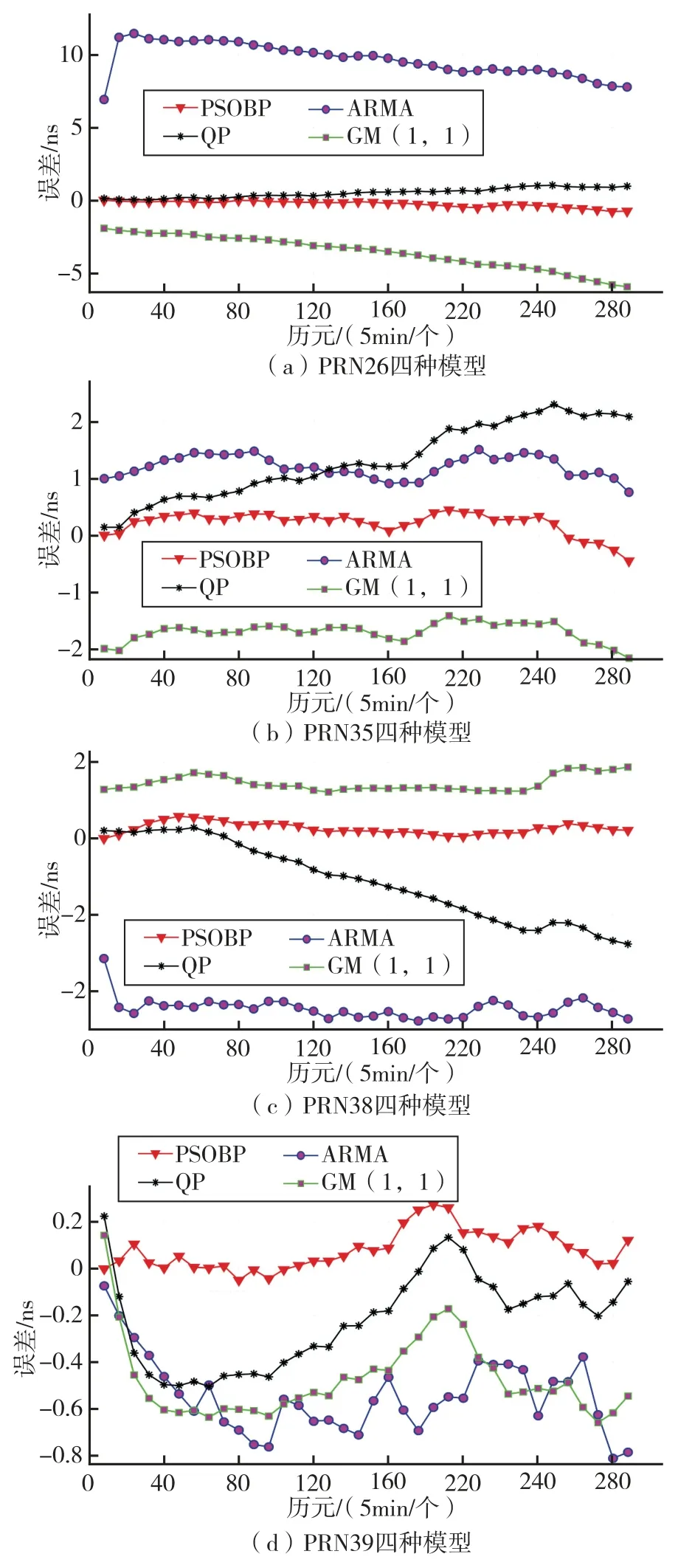
圖4 四種模型預(yù)報(bào)誤差對(duì)比圖Fig.4 Comparison of prediction errors of four models

由圖4 可以看出,改進(jìn)的PSO-BP 模型鐘差預(yù)報(bào)誤差在0 附近波動(dòng),精度更高,波動(dòng)更小。隨著預(yù)報(bào)歷元的增加雖然四種模型會(huì)出現(xiàn)預(yù)報(bào)效果變差的情況,但是改進(jìn)的PSO-BP 模型鐘差預(yù)報(bào)誤差變化要小,預(yù)報(bào)的穩(wěn)定度更好。預(yù)報(bào)誤差的統(tǒng)計(jì)結(jié)果RMSE 和STD 如表3 所示。

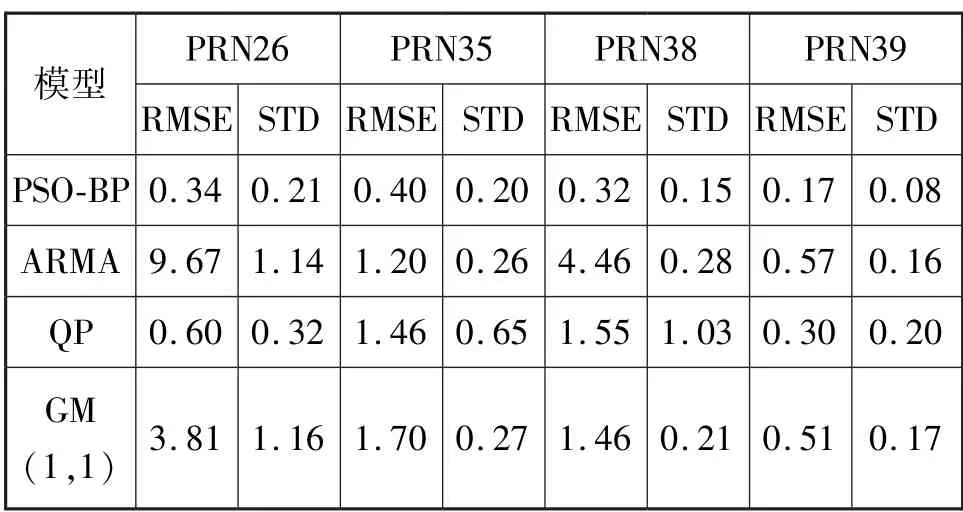
表3 鐘差預(yù)報(bào)誤差統(tǒng)計(jì)表Tab.3 Clock difference forecast error table單位:ns

由表3 可得,PRN26 號(hào)衛(wèi)星:改進(jìn)的PSO-BP 模型相對(duì)于ARMA、QP、GM(1,1)模型的預(yù)報(bào)精度分別提高了96.5%、43.3%、91.1%;預(yù)報(bào)的穩(wěn)定性分別提高了81.6%、34.4%、81.9%。PRN35 衛(wèi)星:改進(jìn)的PSO-BP 相對(duì)其他三種模型預(yù)報(bào)精度分別提高了66.7%、72.6%、76.5%;預(yù)報(bào)的穩(wěn)定性分別提高了23.1%、69.2%、25.9%。PRN38 衛(wèi)星:改進(jìn)的PSO-BP 相對(duì)其他三種模型預(yù)報(bào)精度分別提高了92.8%、79.4%、78.1%;預(yù)報(bào)的穩(wěn)定性分別提高了46.4%、85.4%、28.6%。PRN39 衛(wèi)星:改進(jìn)的PSOBP 相對(duì)其他三種模型預(yù)報(bào)精度分別提高了70.2%、43.3%、66.7%;預(yù)報(bào)的穩(wěn)定性分別提高了50%、60%、52.9%。因此改進(jìn)的PSO-BP 模型無論是預(yù)報(bào)精度還是預(yù)報(bào)的穩(wěn)定性都較傳統(tǒng)的三種模型有很大的提升。

四種模型對(duì)12 顆衛(wèi)星預(yù)報(bào)288 個(gè)歷元的鐘差數(shù)據(jù)的RMSE 值和STD 值統(tǒng)計(jì)結(jié)果如圖5 所示。

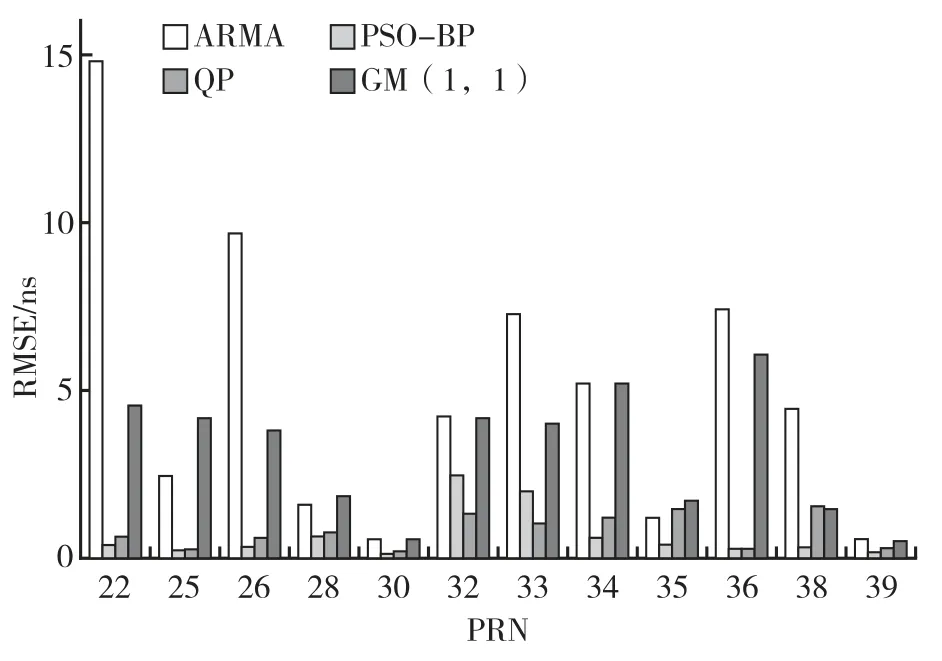
圖5 12 顆BDS 鐘差預(yù)報(bào)RMSE 值對(duì)比圖Fig.5 Comparison of RMSE for 12 BDS clock difference forecasts

從圖5 和圖6 的12 顆衛(wèi)星的鐘差預(yù)測(cè)結(jié)果可以看出:大部分衛(wèi)星,經(jīng)過改進(jìn)的PSO-BP 模型比傳統(tǒng)模型在預(yù)測(cè)精度和穩(wěn)定性方面都有所提高。總體的預(yù)報(bào)精度相對(duì)于ARMA 模型提升了86.5%;穩(wěn)定性提升了61.6%。相對(duì)于QP 模型精度提升了26.8%;穩(wěn)定性提升了6.6%。相對(duì)于GM(1,1)模型精度提升了79%;穩(wěn)定性提升了56.1%。

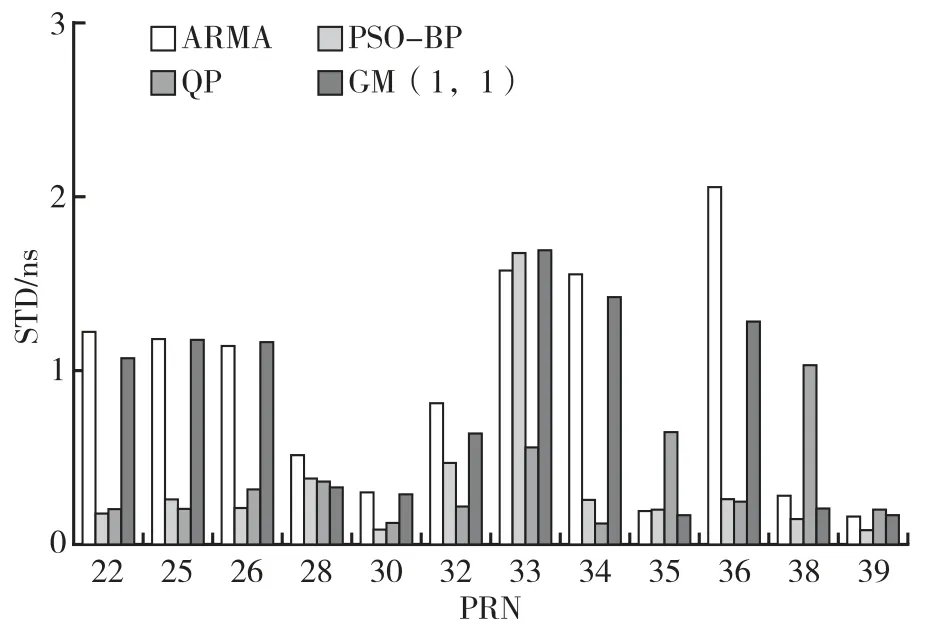
圖6 12 顆BDS 鐘差預(yù)報(bào)STD 值對(duì)比圖Fig.6 Comparison of STD for 12 BDS clock difference forecasts

4 結(jié)束語

為了解決傳統(tǒng)BP 模型在訓(xùn)練過程中陷入局部最優(yōu)解而導(dǎo)致預(yù)測(cè)鐘差不穩(wěn)定的問題,采用粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)模型。為了進(jìn)一步提升粒子群算法計(jì)算速度和搜索精度,改進(jìn)了粒子群算法幾個(gè)重要參數(shù)的生成方法。通過和不同模型的對(duì)比驗(yàn)證了該模型的有效性,說明改進(jìn)的PSO-BP 模型在鐘差預(yù)報(bào)方面有較高的應(yīng)用價(jià)值。