部分連接寬帶毫米波全雙工MIMO系統混合波束成形設計

王庚善,楊志家,李志航,4

1(中國科學院 沈陽自動化研究所 機器人學國家重點實驗室,沈陽 110016) 2(中國科學院 網絡化控制系統重點實驗室,沈陽 110016) 3(中國科學院 機器人與智能制造創新研究院,沈陽 110169) 4(中國科學院大學,北京 100049)

0 引 言

近年來,無線通信技術迅猛發展,5G規模化應用不斷推進,6G相關研究逐步展開,進入萬物互聯時代,在傳輸速率、時延、功耗等方面提出了新的更高要求[1-3].為此,許多新興的物理層技術被廣泛提出并深入研究,其中包括毫米波、大規模多輸入多輸出(Multiple-Input Multiple-Output,MIMO)和全雙工無線通信等[3-5].毫米波是指頻率在26.5-300GHz的電磁波[6],該頻段可以提供豐富的頻譜資源用于無線通信,從根本上解決Sub-6 GHz頻段的頻譜資源緊張問題,從而大幅提升傳輸速率[7];大規模MIMO利用多天線波束成形實現空間復用和高度定向收發數據,可以降低通信干擾,提高通信速率[8,9];全雙工無線通信是指同時同頻進行數據發送與接收,理論上最大可以將頻譜效率提升為傳統時分或頻分雙工的兩倍,同時也可以降低傳輸時延[10].這3種技術分別從不同角度來提高傳輸速率.由于毫米波波長較短,雖然路徑損耗嚴重,但是相比于Sub-6 GHz頻段,在相同的物理尺寸內,可以配備更多天線,因此毫米波全雙工MIMO系統可以將上述3種新興的物理層技術有效地結合起來,是進一步提升傳輸速率的可行方法[11,12].

由于全雙工系統可以同時同頻發送和接收信號,所以其自身的發送信號也會被接收端接收,稱之為“自干擾”信號[10].由于全雙工節點自身接收與發送天線之間的距離遠小于接收天線與遠端節點發送天線之間的距離,因此自干擾信號的強度遠高于有效接收信號.如果無法有效抑制自干擾信號,系統的頻譜效率將會顯著降低.同時,由于毫米波射頻鏈路的成本和功耗較高[7],因此實現毫米波全雙工MIMO通信的關鍵問題是在可接受的硬件功耗和復雜度前提下,如何抑制自干擾信號、提升頻譜效率.自干擾信號通常需要采用被動抑制與主動抑制方法相結合,在空域、模擬域和數字域進行聯合抑制,使剩余自干擾信號的功率在合理范圍[10,13].文獻[14]搭建了第一套完整的毫米波全雙工系統,通過放置天線信號自反射器、設計模擬域專用芯片以及數字域算法,實現了超過80 dB的自干擾抑制,頻譜效率是半雙工系統的1.7倍左右.該研究證明了毫米波全雙工通信的可行性和優越性,但是僅考慮單輸入單輸出系統.由于所提方法需要自反射器和專用芯片,其硬件和計算復雜度會隨著全雙工節點天線數目的二次方增長,所以,該方法很難擴展到毫米波全雙工MIMO系統.在Sub-6 GHz頻段的全雙工MIMO系統中,利用天線選擇、波束選取、零空間投影以及發送和接收波束成形等不需要任何輔助硬件電路的方法進行自干擾抑制和頻譜效率優化被廣泛研究[15-17].這些方法通常基于全數字波束成形來實現,而全數字波束成形要求每根天線連接一條單獨的射頻鏈路,考慮到毫米波射頻鏈路較高的成本和功耗,故基于全數字波束成形的方法在毫米波全雙工MIMO系統中不可行.為了進一步降低系統功耗和硬件復雜度,采用模擬波束成形的毫米波全雙工MIMO系統被提出并研究[11,18].模擬波束成形只需要一條射頻鏈路,所有天線通過移相器與射頻鏈路相連,是硬件復雜度最低、最簡單的毫米波波束成形方法[7].但是,模擬波束成形無法生成多個波束、無法支持多數據流、多用戶通信,嚴重限制了毫米波全雙工通信的性能和應用.

為了進一步提升系統性能同時保持較低功耗和復雜度,基于混合波束成形的毫米波全雙工MIMO系統得到越來越多的關注與研究[19-24].混合波束成形包括模擬和數字波束成形兩部分,其中模擬波束成形通常由毫米波頻段的移相器網絡實現,數字波束成形則在基帶完成[7].相比于全數字波束成形,混合波束成形需要更少的射頻鏈路,功耗和復雜度低;相比于模擬波束成形,混合波束成形支持多數據流、多用戶通信,性能更優.根據天線與射頻鏈路的連接方式,混合波束成形結構又分為全連接結構(每根天線通過移相器與每條射頻鏈路相連)和部分連接結構(每根天線通過移相器僅與一條射頻鏈路相連).全連接結構的性能更優,但是部分連接的功耗和硬件復雜度更低.當前關于毫米波全雙工MIMO系統混合波束成形的研究多集中于全連接結構[19-22].文獻[19]以最小化自干擾信號的功率作為優化目標,利用拉格朗日乘子法和子空間分解方法求出混合波束成形矩陣,所提方法能夠將自干擾信號抑制超過30 dB,但是該研究僅考慮窄帶系統和無限精度移相器.文獻[20]提出了基于稀疏空間編碼和零空間投影的混合波束成形方法來抑制自干擾信號,能夠有效提升頻譜效率.在后續研究中,該方法又被進一步擴展至寬帶毫米波全雙工系統[21].文獻[22]考慮采用有限精度移相器的毫米波全雙工MIMO系統,以最大化系統頻譜效率作為優化目標,采用懲罰對偶分解框架進行混合波束成形設計,得到近似最優解,然而該研究僅考慮單天線用戶和窄帶系統.針對部分連接毫米波全雙工MIMO系統,當前研究相對較少[23,24].文獻[23]提出了基于半正定松弛(Semidefinite Relaxation,SDR)、交替最小化和零空間投影的自干擾抑制混合波束成形方法,在特定條件下,該方法實現的頻譜效率要優于半雙工通信.該研究證明了部分連接毫米波全雙工通信的可行性,但是計算復雜度較高、僅考慮窄帶系統和無限精度移相器.文獻[24]考慮寬帶毫米波全雙工系統,提出了波束成形和自干擾抑制聯合設計方法.該方法能夠有效抑制自干擾信號、提高接收功率,但是在建模時并沒有考慮與節點之間距離相關的上下行信道的實際路徑損耗.

針對上述相關研究中存在的不足,本文對部分連接寬帶毫米波全雙工MIMO系統的混合波束成形問題進行研究,主要創新點和貢獻總結如下:

1)考慮更加符合實際通信場景的部分連接毫米波全雙工MIMO系統,即有限精度移相器、寬帶毫米波系統和上下行信道的實際路徑損耗.

2)提出了一種可行的三階段混合波束成形方法.首先,不考慮自干擾信號,利用上行與下行各子信道的奇異值分解和注水功率分配算法得到各子帶最優全數字發送和接收波束成形矩陣;然后,根據得到的全數字波束成形矩陣,利用矩陣分解方法求出滿足部分連接結構的模擬波束成形矩陣和各子帶數字波束成形矩陣;最后,提出利用最小均方誤差(Minimum Mean Square Error,MMSE)準則更新各子帶數字接收波束成形矩陣來處理剩余自干擾信號,降低其引起的頻譜效率損失.

3)理論分析表明,所提方法的計算復雜度要低于相關算法;同時,仿真結果表明,所提方法的頻譜效率要高于相關對比方法和理想半雙工毫米波通信.當移相器精度為6位、信噪比為20 dB時,采用所提方法的部分連接寬帶毫米波全雙工MIMO系統實現的頻譜效率大約是理想半雙工毫米波系統的1.41倍.

本文所用數學符號介紹如下:粗體小寫和大寫字母分別表示向量和矩陣,AH,A-1,A?,Tr{A}和‖A‖F分別表示矩陣A的共軛轉置、逆、廣義逆、跡和Frobenius范數,A(i,:),A(:,j)和A(i,j)分別表示矩陣A的第i行、第j列和位于第i行、第j列的元素.IN表示N×N維單位矩陣,0N(0M×N)表示N×N(M×N)維零矩陣,M×N表示M×N維復數矩陣構成的線性空間.CN(μ,Σ)表示服從均值為μ、方差為Σ的循環對稱復高斯隨機向量的分布,N(μ,σ2)表示服從均值為μ、方差為σ2的實高斯隨機變量的分布.blkdiag{a1,a2,…,aN}表示由向量a1,a2,…,aN構成的塊狀對角矩陣,|·|表示標量的絕對值或矩陣的行列式,「·表示向上取整即取超過參數的最小整數,{·}和Re{·}分別表示取參數的期望和實部.

1 系統模型與問題描述

1.1 系統模型

本文考慮單蜂窩寬帶毫米波全雙工MIMO系統,包括一個全雙工基站BS和兩個半雙工移動端MS1和MS2,如圖1所示.其中,基站和移動端都采用部分連接結構,寬帶信號采用正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)實現.全雙工基站BS配備NT根發送天線、NR根接收天線,發送和接收射頻鏈路的數目均為NRF;移動端MS1配備MT根發送天線和MRF條發送射頻鏈路,移動端MS2配備MR根接收天線和MRF條接收射頻鏈路.OFDM子載波的數目為K,每個子載波的平行數據流數目均為Ns.由毫米波混合波束成形結構中數據流、射頻鏈路和天線數目之間的關系可知,Ns≤NRF≤min{NT,NR},Ns≤MRF≤min{MT,MR}.正常工作時,全雙工基站BS在上行鏈路接收移動端MS1的發送信號,同時在下行鏈路向移動端MS2發送信號.由于毫米波信道的路徑損耗嚴重,為了處理簡單,本文假設兩移動端MS1和MS2之間的距離足夠遠,因此,可以忽略二者之間的相互干擾.

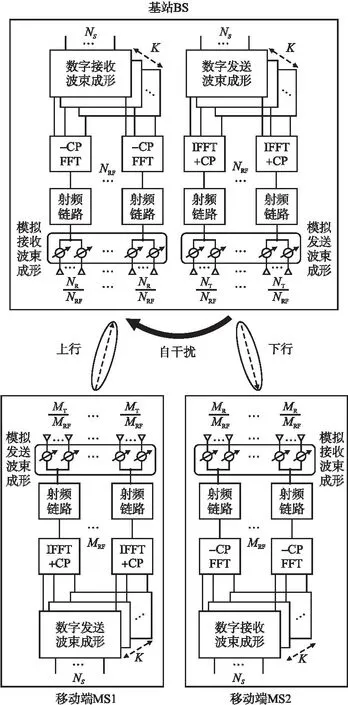
圖1 部分連接寬帶毫米波全雙工MIMO系統Fig.1 Wideband mmWave full-duplex MIMO system with partially-connected structures

在上行鏈路中,移動端MS1第k個子帶的發送符號向量為sU[k]∈Ns×1,滿足首先,發送符號向量sU[k]經過該子帶的數字發送波束成形矩陣FBBU[k]∈MRF×Ns預編碼,再通過K點快速傅里葉逆變換(Inverse Fast Fourier Transform,IFFT)變為時域信號,并增加循環前綴(Cyclic Prefix,CP),以保證子載波間的正交性同時消除符號間干擾;然后,該信號經發送射頻鏈路上變頻至毫米波頻段,通過模擬發送波束成形矩陣FRFU∈MT×MRF處理之后,得到移動端MS1的最終發送信號;最后,該發送信號經過上行信道發送至基站BS.同理,在下行鏈路中,基站第k個子帶的發送符號向量sD[k]∈Ns×1,滿足經過該子帶的數字發送波束成形矩陣FBBD[k]∈NRF×Ns、K點IFFT增加CP以及模擬發送波束成矩陣FRFD∈NT×NRF處理之后,得到基站BS的最終發送信號,該信號經過下行信道發送至移動端MS2.

由于基站BS工作于全雙工模式,因此,不但能夠通過上行信道接收來自移動端MS1的信號,而且能夠通過自干擾信道接收自干擾信號.該接收信號首先經過模擬接收波束成形矩陣WRFU∈NR×NRF處理,再由接收射頻鏈路下變頻至基帶;然后,通過移除CP并進行快速傅里葉變換(Fast Fourier Transform,FFT)變為頻域信號,最后,經過數字接收波束成形矩陣WBBU[k]∈NRF×Ns,k=1,2,…,K,處理之后,得到每個子帶的最終基帶接收信號.基站BS第k個子帶的基帶接收信號可以具體表示為:

(1)

其中,HU[k]∈NR×MT和HSI[k]∈NR×NT分別表示第k個子帶的上行信道和自干擾信道,表示基站BS接收端第k個子帶的加性高斯白噪聲.WU[k]=WRFUWBBU[k]表示基站接收端第k個子帶的整體混合接收波束成形矩陣,FU[k]=FRFUFBBU[k]和FD[k]=FRFDFBBD[k]則分別表示移動端MS1和基站BS發送端第k個子帶的整體混合發送波束成形矩陣.在基站BS第k個子帶的接收信號即公式(1)中,第1項表示從移動端MS1接收到的有效信號,第2項表示基帶噪聲信號,第3項表示自干擾信號.同理,半雙工移動端MS2的接收信號經過模擬接收波束成形矩陣WRFD∈MR×MRF、移除CP和K點FFT以及各子帶數字接收波束成形矩陣WBBD[k]∈MRF×Ns,k=1,2,…,K,處理之后,得到第k個子帶的基帶接收信號為:

(2)

其中,HD[k]∈MR×NT表示第k個子帶的下行信道,表示移動端MS2第k個子帶的加性高斯白噪聲,WD[k]=WRFDWBBD[k]則表示移動端MS2第k個子帶的整體混合接收波束成形矩陣.

1.2 信道模型

由于基站BS與移動端MS1(MS2)之間的距離足夠遠,所以,上行和下行信道充分滿足遠場條件.為了準確描述毫米波MIMO-OFDM信道特征,本文采用抽頭延遲線寬帶信道模型[25],其中每個抽頭信道又建模為Saleh-Valenzuela(SV)空間信道模型[26,27].具體地,第d個抽頭的信道模型如下:

(3)

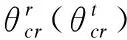
(4)

其中,D表示CP的長度.因此,可以根據上行與下行鏈路中發送和接收天線數目、散射簇和路徑數目以及到達角、離開角等來更改式(3)中的參數,建模各抽頭上行和下行信道;然后,根據式(4)得到上行與下行各子帶信道.

由于全雙工基站BS發送和接收天線陣列距離較近,無法充分滿足遠場條件,所以自干擾信道模型必須將近場效應考慮在內,通常建模為萊斯衰減信道[11,21,24],其第d個抽頭的表達式為:

(5)

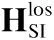
(6)

其中,ρ為歸一化因子,保證為載波波長,rmn表示基站BS第m根接收天線與第n根發送天線之間的距離,可以根據文獻[11]中的圖2,利用余弦定理求出.表示自干擾信道第d個抽頭的非視距傳播部分,滿足遠場條件,所以,可用式(3)表示的SV空間信道模型進行建模.對時域抽頭自干擾信道進行DFT,如式(4)所示,可得頻域各子帶自干擾信道.

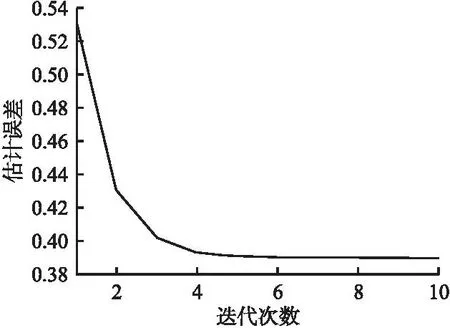
圖2 第2階段混合波束成形的收斂性Fig.2 Convergence of the hybrid beamforming design in the second stage

1.3 部分連接結構

1.4 問題描述

假設每個子帶的發送信號均為高斯信號,則第k個子帶的上行頻譜效率RU[k]和下行頻譜效率RD[k]分別定義為:

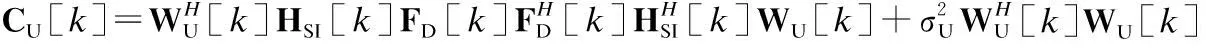
本文假設上行、下行和自干擾信道的狀態信息在基站BS已知且接收射頻鏈路模數轉換器(Analog-to-Digital Converters,ADCs)的動態范圍無限大[19-21],考慮發送功率約束、模擬波束成形矩陣非零元素的有限精度約束、單位模長約束以及由部分連接結構引入的約束,旨在通過聯合設計全雙工基站BS和半雙工移動端MS1、MS2的混合波束成形矩陣來最大化系統的整體頻譜效率.該問題的數學表述如下:

(7a)

(7b)

(7c)

FRFU(i,j)∈D,|FRFU(i,j)|=1,?(i,j)∈FU

(7d)

FRFD(i,j)∈D,|FRFD(i,j)|=1,?(i,j)∈FD

(7e)

WRFU(i,j)∈D,|WRFU(i,j)|=1,?(i,j)∈WU

(7f)

WRFD(i,j)∈D,|WRFD(i,j)|=1,?(i,j)∈WD

(7g)

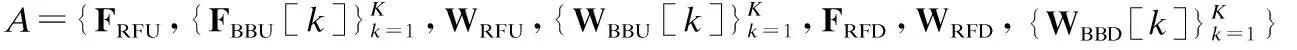
2 三階段混合波束成形方法

針對非凸優化問題(7),本文提出了一種可行的混合波束成形方法.雖然所提方法并不能求出最優解,但可以求出一組考慮系統性能的可行解.所提混合波束成形方法共包括3個階段,詳述如下.

2.1 不考慮自干擾信號的最優全數字波束成形

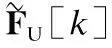
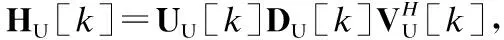
(8a)

(8b)

其中,PU[k]∈Ns×Ns為對角矩陣,每個對角線元素表示在移動端MS1通過注水算法分配給第k個子帶中對應數據流的發送功率,滿足同理,若下行第k個子信道HD[k]的奇異值分解為其中DD[k]∈MR×NT表示對角矩陣,其對角線元素為遞減排列的奇異值,UD[k]∈MR×MR和VD[k]∈NT×NT分別表示由左奇異向量和右奇異向量構成的酉陣,則基站BS發送端第k個子帶的最優全數字發送波束成形矩陣和移動端MS2第k個子帶的最優全數字接收波束成形矩陣分別為:

(9a)

(9b)

其中PD[k]∈Ns×Ns為對角矩陣,其對角線元素表示在基站BS發送端利用注水算法分配給第k個子帶中對應數據流的發送功率,滿足

2.2 不考慮自干擾信號的混合波束成形

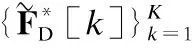
(10a)

(10b)

FRFD(i,j)∈D,|FRFD(i,j)|=1,?(i,j)∈FD

(10c)

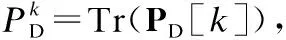
2.2.1 更新模擬發送波束成形矩陣FRFD

當固定其他變量同時移除常數項時,問題(10)關于模擬發送波束成形矩陣FRFD的子問題為:

(11)

s.t.(10c)

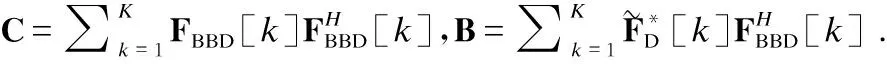
(12)

s.t.(10c)

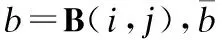
(13)

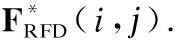
由于各子帶的數字發送波束成形矩陣相互獨立,所以,當其他變量固定時,問題(10)關于第k個子帶的數字發送波束成形矩陣FBBD[k]的子問題為:

(14)

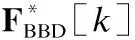
(15)

同理,可求出其他各子帶數字發送波束成形矩陣.交替迭代更新模擬和各子帶數字發送波束成形矩陣,直至滿足某一終止條件.最后,對數字發送波束成形矩陣FBBD[k],k=1,2,…,K,進行如下功率歸一化,以滿足發送功率約束:

(16)

2.3 MMSE準則更新各子帶數字接收波束成形矩陣

前兩階段求得的混合波束成形設計并沒有考慮自干擾信號,所以,剩余自干擾信號存在,并且會造成較大的頻譜效率損失.在考慮復雜度前提下,線性MMSE接收機是實現系統最大傳輸速率的最優數字接收機[28,31].因此,為了有效降低自干擾信號對頻譜效率的影響,本階段提出在已經求得的混合波束成形設計的基礎上,利用MMSE準則來更新基站BS接收端和移動端MS2各子帶的數字接收波束成形矩陣.首先,基站BS接收端和移動端MS2第k個子帶的均方差矩陣EU[k]和ED[k]分別定義如下:

EU[k]=

ED[k]=

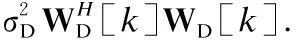
根據上述定義,當其他變量保持不變同時移除常數項時,關于數字接收波束成形矩陣WBBU[k]的最小均方誤差問題如下:

(17)

其中,

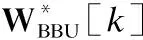
(18)

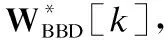
至此,針對部分連接寬帶毫米波全雙工MIMO系統,本文所提出的三階段混合波束成形設計完成,其中,第2階段不考慮自干擾信號的混合波束成形設計總結于算法1.由于第3階段采用MMSE準則更新各子帶數字接收波束成形矩陣,所以,將本文提出的混合波束成形方法命名為WBFD_PCS_MMSE,其具體細節總結于算法2.

算法1.第2階段不考慮自干擾信號的混合波束成形設計

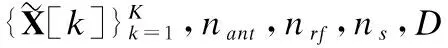
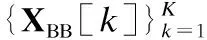
1.初始化XRF∈nant×nrf為塊狀對角矩陣,非零元素滿足有限精度和單位模長約束,設置最大迭代次數L和誤差精度δ,l=0;

2.nsub=nant/nrf

3.repeat

4.i=0;

5.repeat

7.until(i>nant)

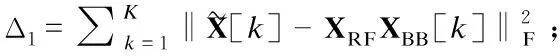
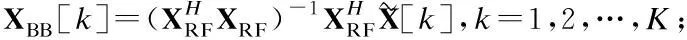
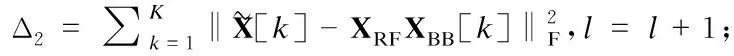
11.until(|Δ1-Δ2|<δ或l>L)

算法2.部分連接寬帶毫米波全雙工MIMO系統三階段混合波束成形方法WBFD_PCS_MMSE

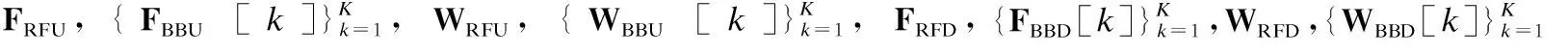
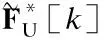
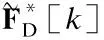
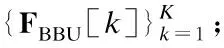
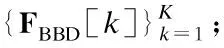
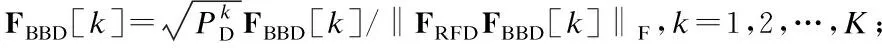
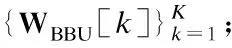
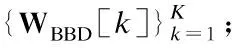
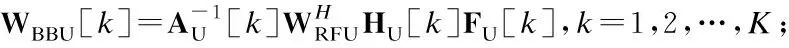
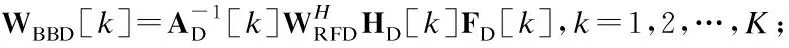
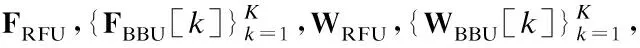
3 算法復雜度分析

本節以所需復數乘法的次數作為算法復雜度的量度,對本文提出的部分連接寬帶毫米波全雙工MIMO系統混合波束成形方法WBFD_PCS_MMSE的算法復雜度進行分析.所提方法包括3階段,各階段算法復雜度具體分析如下:

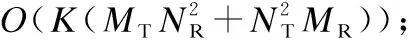
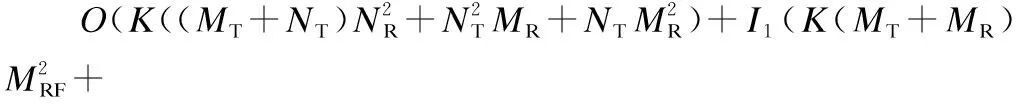
(19)

其中,(a)成立的條件是假設基站BS發送和接收天線的數目要遠大于移動端MS1和MS2的天線數目,同時基站BS的射頻鏈路數目大于等于移動端MS1和MS2的射頻鏈路數目.

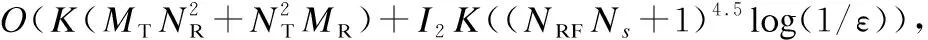
4 仿真結果與分析

本節將利用蒙特卡洛仿真方法對提出的部分連接寬帶毫米波全雙工MIMO系統混合波束成形方法WBFD_PCS_MMSE的性能進行評估.為了更好地展現所提方法的性能,考慮如下對比:

1)Ideal FD:理想全雙工系統,假設沒有自干擾信號同時采用全數字波束成形設計;

2)FD_BFC:文獻[21]中提出的基于自干擾抑制的全連接寬帶毫米波全雙工系統混合波束成形設計;

3)FD_MinSIP:將文獻[19]中提出的基于自干擾信號功率最小化的混合波束成形方法擴展至全連接寬帶毫米波全雙工系統;

4)FD_PCS_JBIC:文獻[24]中提出的部分連接寬帶毫米波全雙工系統聯合優化接收功率和自干擾抑制的混合波束成形方法;

5)FD_PCS_SDRNSP:將文獻[23]中提出的部分連接毫米波全雙工系統的自干擾抑制混合波束成形方法擴展到對應的部分連接寬帶毫米波全雙工MIMO系統;

6)Ideal HD:理想半雙工系統,基站BS所有天線均用于半雙工通信,同時采用全數字波束成形設計.

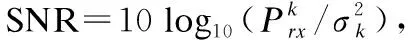
4.1 收斂性

4.2 頻譜效率

圖3比較了不同方法的頻譜效率隨信噪比的變化,其中,WBFD_PCS_NoMMSE表示只采用所提混合波束成形設計的前兩階段所實現的頻譜效率.從圖中可以看出,本文提出的三階段混合波束成形方法WBFD_PCS_MMSE的頻譜效率要明顯優于WBFD_PCS_NoMMSE,說明所提方法的第3階段必不可少,該階段可以有效抑制剩余自干擾信號、提升頻譜效率.從圖中也可以觀察到,本文所提方法WBFD_PCS_MMSE的頻譜效率要比方法WBFD_BFC差,主要原因是后者為全連接毫米波全雙工系統,能夠提供更好的波束成形增益;雖然方法WBFD_MinSIP也考慮全連接毫米波全雙工系統,但是由于沒有對矩陣分解引起的剩余自干擾信號進行處理,所以該方法的頻譜效率要比本文所提方法差.同時,可以看到本文所提方法實現的頻譜效率要優于WBFD_PCS_JBIC和WBFD_PCS_SDRNSP這兩種針對部分連接寬帶毫米波全雙工MIMO系統的混合波束成形方法.通過第4節分析可知,這兩種對比方法的實際計算復雜度要高于本文所提方法,因此本文所提方法WBFD_PCS_MMSE具有一定的優越性.此外,當信噪比高于0dB時,本文所提方法的頻譜效率要高于理想半雙工系統,證明了部分連接寬帶毫米波全雙工MIMO通信的可行性;當信噪比為20dB時,本文所提方法的頻譜效率大約是理想半雙工通信的1.41倍.

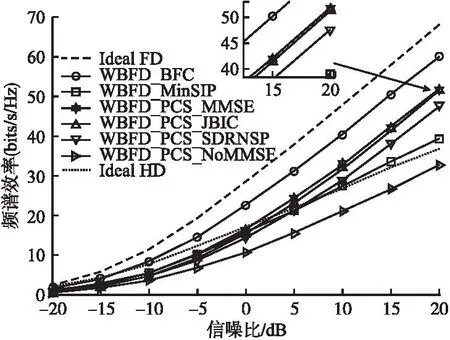
圖3 頻譜效率隨信噪比的變化Fig.3 Spectral efficiency versussignal-to-noise ratio

圖4對比了不同方法的頻譜效率隨基站BS射頻鏈路數目的變化,其中信噪比等于10dB.對于部分連接結構,為了保證天線數目可以被射頻鏈路數目整除,基站BS射頻鏈路數目NRF={4,8,16}.隨著基站BS射頻鏈路數目的增加,模擬和數字波束成形的自由度增加,可以更好地抑制自干擾信號同時提高波束成形增益,因此,圖4中采用本文所提方法WBFD_PCS_MMSE的部分連接寬帶毫米波全雙工MIMO系統的頻譜效率上升.同時,在任何射頻鏈路數目條件下,本文所提方法WBFD_PCS_MMSE的頻譜效率都要優于考慮相同系統的對比方法WBFD_PCS_JBIC和WBFD_PCS_SDRNSP.當射頻鏈路數目較少時,如NRF=4,由于仿真實驗中的平行數據流數目Ns=3,所以,沒有充足的自由度同時進行有效自干擾抑制和數據流傳輸.因此,本文所提方法WBFD_PCS_MMSE的頻譜效率要低于基于方法WBFD_MinSIP的全連接毫米波全雙工系統,甚至要低于理想半雙工系統.當射頻鏈路數目大于等于6時,所提方法的頻譜效率要高于方法WBFD_MinSIP和理想半雙工系統,但是仍低于方法WBFD_BFC,具體原因與圖3類似,這里不再贅述.

圖4 頻譜效率隨基站射頻鏈路數目的變化Fig.4 Spectral efficiency versus the number ofradio-frequency chains at the base station

圖5描述了不同方法的頻譜效率隨基站BS天線數目的變化,其中信噪比等于10dB.圖中橫坐標表示基站BS總的天線數目,其中一半是發送天線、另一半是接收天線.從圖中可以觀察到,隨著天線數目的增加,本文所提方法WBFD_PCS_MMSE的頻譜效率上升,這是因為更多的天線能夠提供更高的天線多樣性和自由度,從而可以更好地抑制自干擾信號,同時提高波束成形增益.相比于考慮相同系統的混合波束成形方法WBFD_PCS_JBIC和WBFD_PCS_SDRNSP,本文所提方法WBFD_PCS_MMSE能夠實現更高的頻譜效率,但與方法WBFD_PCS_JBIC的頻譜效率差距逐漸減小.本文所提方法的頻譜效率比基于方法WBFD_BFC的全連接毫米波全雙工系統差,但是二者之間的頻譜效率差距先上升后下降,在天線數目為128時最大,大約為9.1 bits/s/Hz.同時,本文所提方法的頻譜效率要明顯高于采用方法WBFD_MinSIP的全連接毫米波全雙工系統和理想半雙工系統.

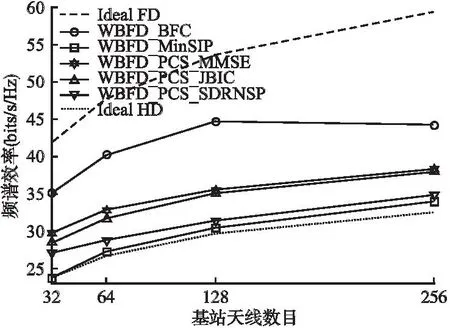
圖5 頻譜效率隨基站天線數目的變化Fig.5 Spectral efficiency versus the number of antennas at the base station

圖6提供了不同方法的頻譜效率隨子載波數目的變化,其中信噪比等于10dB.由圖可知,隨著子載波數目的增加,本文所提方法WBFD_PCS_MMSE的頻譜效率略微下降.這是因為子載波數目的增加會引起信道的頻率選擇性上升,從而更難設計出滿足所有子載波信道的模擬發送和接收波束成形矩陣,在一定程度上降低了自干擾抑制能力和波束成形增益,造成頻譜效率下降.此外,從圖6中可以得到與圖3和圖5中類似的結論,即本文所提方法WBFD_PCS_MMSE的頻譜效率比方法WBFD_BFC差,但是要明顯優于考慮相同系統的對比方法WBFD_PCS_JBIC和WBFD_PCS_SDRNSP,以及WBFD_MinSIP和理想半雙工系統.

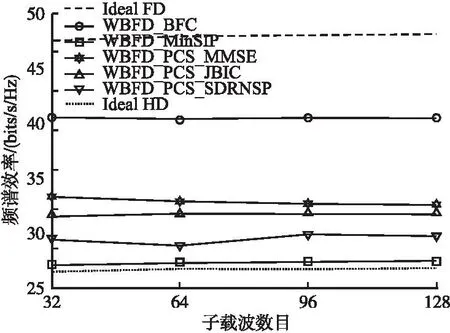
圖6 頻譜效率隨子載波數目的變化Fig.6 Spectral efficiency versus the number of subcarriers

圖7仿真了本文所提方法WBFD_PCS_MMSE采用不同精度移相器實現的頻譜效率隨信噪比的變化.從圖中可以看出,隨著移相器精度的提高,所提方法的頻譜效率先上升后逐漸飽和,原因是高精度的移相器可以提供更豐富的碼本,從而實現更優的模擬波束成形.當信噪比高于10 dB時,所提方法即使采用1位精度移相器實現的頻譜效率也要高于理想半雙工系統,這與文獻[22]中針對全連接毫米波全雙工系統的結論一致;當移相器精度超過4位時,所提方法能夠實現接近于無窮精度移相器的頻譜效率,再提高移相器精度對頻譜效率的提升不明顯.因此,權衡成本、功耗和性能,對于采用本文所提方法的部分連接寬帶毫米波全雙工MIMO系統建議使用4位精度移相器.當信噪比等于20 dB時,所提方法采用4位精度移相器可以實現理想全雙工系統大約76.2%的頻譜效率,同時大約是理想半雙工系統頻譜效率的1.41倍.

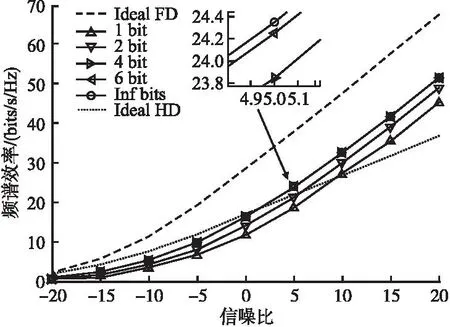
圖7 不同精度移相器的頻譜效率隨信噪比的變化Fig.7 Spectral efficiency using phase shifters with different resolutions versus SNR

5 結 論

本文對采用有限精度移相器的部分連接寬帶毫米波全雙工MIMO系統的混合波束成形問題進行研究,提出了一種可行的三階段混合波束成形方法,該方法可以有效抑制自干擾信號同時實現較優的頻譜效率.分析表明,所提方法的算法復雜度要低于相關對比方法;仿真結果表明,所提方法具有較好的收斂性,能夠實現比相關研究和理想半雙工毫米波通信更高的頻譜效率.

在后續工作中,將進一步對考慮ADC有限動態范圍和用戶間相互干擾的部分連接寬帶毫米波全雙工MIMO系統的混合波束成形問題進行研究.