污泥干燥特性實(shí)測(cè)及預(yù)測(cè)模型研究

王振宇　王強(qiáng)　劉東　王令　陳永燦

摘要：污泥脫水干化是污泥資源化利用的重要環(huán)節(jié)，目前缺乏通識(shí)性的污泥干燥模型。實(shí)驗(yàn)分析了干燥溫度、相對(duì)濕度、污泥厚度、干燥時(shí)間等因素對(duì)污泥干燥過(guò)程的影響，比較了常用的5種薄層干燥模型對(duì)污泥干燥過(guò)程的擬合效果，建立了一種 BP 神經(jīng)網(wǎng)絡(luò)污泥干燥預(yù)測(cè)模型，并與傳統(tǒng)的擬合效果較優(yōu)的Midilli模型進(jìn)行了預(yù)測(cè)精度比較。結(jié)果表明：當(dāng)污泥低溫干燥時(shí)，溫度、相對(duì)濕度對(duì)污泥干燥有顯著影響，相對(duì)濕度越高、溫度越低，污泥干燥速率越慢；Midilli模型決定系數(shù)高、卡方系數(shù)和均方根誤差均較小，是5種常用薄層干燥模型中擬合效果最好的模型，其與實(shí)驗(yàn)結(jié)果誤差在15%以內(nèi)；BP 神經(jīng)網(wǎng)絡(luò)污泥干燥預(yù)測(cè)模型能很好預(yù)測(cè)污泥的干燥過(guò)程，預(yù)測(cè)結(jié)果與實(shí)驗(yàn)測(cè)試結(jié)果誤差在5%以內(nèi)，具有比Midilli模型更高的預(yù)測(cè)精度。BP 神經(jīng)網(wǎng)絡(luò)污泥干燥預(yù)測(cè)模型為污泥干燥過(guò)程模擬提供了一種新的方法。

關(guān)鍵詞：污泥薄層干燥模型 BP 神經(jīng)網(wǎng)絡(luò)污泥干燥預(yù)測(cè)模型

中圖分類號(hào)：X703? 文獻(xiàn)標(biāo)志碼：A? 文章編號(hào)：1671-8755（2024）01-0066-09

Study on the Measurement and Prediction Model of Sludge Drying Characteristics

WANG Zhenyu1 ， WANG Qiang2 ， LIU Dong2 ， WANG Ling2 ， CHEN Yongcan1

（1. School ofEnvironment and Resource ， Southwest University ofScience and Technology ， Mianyang621010 ， Sichuan ， China;2. School ofCivil Engineering and Architecture ， Southwest University ofScience and Technology ， Mianyang 621010 ， Sichuan ， China ）

Abstract： Sludge dewatering and drying are crucial steps in the resource utilization of sludge . There is currently a lack of a comprehensive drying model of sludge . The effects of drying temperature ， relative humidity ， sludge thickness ， and drying time on drying sludge were analyzed in the experiment. The fitting effects of five commonly used thin-layer drying models on the sludge drying process were compared . A BP neural network model was established for predicting sludge drying. This was compared with the Midillimodel ， which has traditionally shown better fitting results for prediction accuracy. The results indicate that the drying of sludge is significantly affected by temperature and relative humidity when it is dried at low temperatures . The higher the relative humidity and the lower the temperature ， the slower the rate at which the sludge dries . The Midilli model has a high coefficient of determination ， and its chi-square and RMSE values are relatively low. It is the best-fitting model among the five commonly used thin-layer drying mod- els . The error compared to the experimental results is within 15%. The BP neural network sludge drying prediction model can predict the sludge drying process very well . The prediction results have less than 5% errors compared to the experimental results . The model has a higher predictive accuracy than that ofthe Midillimodel . The BP neural network model for sludge drying prediction provides a new method to simulate the sludge drying process .

Keywords ： Sludge; Thin layer drying model; BP neural network model for sludge drying prediction

日常生活和工業(yè)生產(chǎn)是城市污水的主要來(lái)源。在污水處理過(guò)程中，不可避免地會(huì)產(chǎn)生污泥。污泥是由有機(jī)碎片、細(xì)菌和無(wú)機(jī)顆粒組成的高含水率非均質(zhì)體[1-3]。污泥中的無(wú)機(jī)組分除了一些重金屬等有害物質(zhì)外，還有大部分是能夠改善土地肥力、促進(jìn)植物生長(zhǎng)的有益物質(zhì)，同時(shí)污泥中的有機(jī)質(zhì)含量非常豐富，具有較高熱值，是一種潛在的生物肥料及燃料，可以應(yīng)用到農(nóng)業(yè)生產(chǎn)中。另一方面，污泥中含有有害的有機(jī)化合物、病原微生物，未經(jīng)處理直接排放到環(huán)境中會(huì)造成嚴(yán)重污染。如果不消除有害化合物（如砷）并通過(guò)一些專門的處理降低污染物濃度，無(wú)機(jī)鹽會(huì)破壞土壤中的離子平衡，導(dǎo)致土壤中的養(yǎng)分失衡，無(wú)法實(shí)現(xiàn)污泥的回收利用。

隨著城市化進(jìn)程的持續(xù)推進(jìn)和污水處理廠數(shù)量及規(guī)模的增長(zhǎng)，產(chǎn)生了大量高含水率污泥[4]。污泥含水率高，含有細(xì)菌、病毒[5]和重金屬，會(huì)造成安全、運(yùn)輸和利用方面的問(wèn)題。干燥是解決這些問(wèn)題的關(guān)鍵步驟。污泥干燥是一個(gè)復(fù)雜的熱濕傳遞過(guò)程，該過(guò)程受多種因素的影響，如加熱形式[6]、污泥預(yù)處理[7]、生物質(zhì)添加[8]、污泥來(lái)源[9]、厚度[10]、空氣參數(shù)[11]等。為了掌握污泥干燥的規(guī)律，研究者們提出了許多描述干燥過(guò)程的數(shù)學(xué)模型，其中薄層干燥模型受到廣泛關(guān)注。Henderson 等[12]對(duì)谷物的干燥特性進(jìn)行研究，提出了 Henderson and Pabis 薄層干燥經(jīng)驗(yàn)公式。Midilli等[13]根據(jù)實(shí)驗(yàn)提出了一種新的薄層干燥模型。Ghazanfari 等[14]在Midilli模型的基礎(chǔ)上進(jìn)行了修正。C orzo [15]在前人模型的基礎(chǔ)上進(jìn)行了修改優(yōu)化，賦予了方程參數(shù)意義，提出了 Weibull 模型，使其更為準(zhǔn)確地描述物料的干燥現(xiàn)象。目前雖然對(duì)干燥模型進(jìn)行了大量研究，但尚未發(fā)現(xiàn)能廣泛適用于污泥干燥的干燥模型。

近年來(lái)，隨著計(jì)算機(jī)科學(xué)的快速發(fā)展，利用神經(jīng)網(wǎng)絡(luò)技術(shù)進(jìn)行智能決策的方法得到了迅速推廣。神經(jīng)網(wǎng)絡(luò)算法因具有很強(qiáng)的計(jì)算能力和學(xué)習(xí)能力，被應(yīng)用于各個(gè)領(lǐng)域進(jìn)行信息處理。更重要的是，BP 神經(jīng)網(wǎng)絡(luò)適用于多輸入變量和多數(shù)據(jù)集模型的構(gòu)建。伍丹華等[16]使用江蘇省2009-2013年糧食產(chǎn)量相關(guān)數(shù)據(jù)訓(xùn)練 BP 神經(jīng)網(wǎng)絡(luò)，通過(guò)2014-2018年糧食產(chǎn)量數(shù)據(jù)檢驗(yàn)網(wǎng)絡(luò)，網(wǎng)絡(luò)的誤差小于3% ， 得出 BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)糧食產(chǎn)量精度高的結(jié)論。張利娟等 [17]利用全部試驗(yàn)數(shù)據(jù)建立了真空干燥各工藝參數(shù)與小麥含水率之間的 BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型，驗(yàn)證結(jié)果表明小麥含水率的預(yù)測(cè)結(jié)果與實(shí)測(cè)值誤差小于5.2% ， 所建立的 BP 神經(jīng)網(wǎng)絡(luò)模型能較好反映真空干燥工藝參數(shù)與含水率之間的復(fù)雜非線性關(guān)系。 Han 等[18]建立了合金本構(gòu)關(guān)系的人工神經(jīng)網(wǎng)絡(luò)模型，與傳統(tǒng)的 Arrhenius 型模型相比誤差較小。目前未見(jiàn)基于人工神經(jīng)網(wǎng)絡(luò)的污泥干燥預(yù)測(cè)模型的報(bào)道。

本文以綿陽(yáng)地區(qū)市政污泥為研究對(duì)象，搭建污泥干燥測(cè)試實(shí)驗(yàn)平臺(tái)，研究了低溫（不超過(guò)60℃）情況下，不同環(huán)境參數(shù)（溫度、相對(duì)濕度）和污泥厚度對(duì)干燥性能的影響。以實(shí)驗(yàn)結(jié)果為數(shù)據(jù)源建立污泥干燥模型，將5種常用的傳統(tǒng)薄層干燥模型方法與通過(guò) BP 神經(jīng)網(wǎng)絡(luò)建立的污泥干燥模型進(jìn)行比較，并闡述了在 BP 神經(jīng)網(wǎng)絡(luò)中不同的訓(xùn)練算法和隱藏神經(jīng)元數(shù)量對(duì)模型預(yù)測(cè)精度的影響。

1 實(shí)驗(yàn)方法

1.1 材料

實(shí)驗(yàn)污泥取自四川省綿陽(yáng)市永興生活污泥處理廠，通過(guò)離心脫水設(shè)備去除存在于污泥顆粒間以及顆粒內(nèi)的水，從而使液態(tài)的污泥變成半固態(tài)，形態(tài)如圖1所示。污泥成分主要是由有機(jī)殘片、細(xì)菌菌體、無(wú)機(jī)顆粒、膠體等組成的極其復(fù)雜的非均質(zhì)體。污泥的初始平均濕基含水率約為84%。

1.2 實(shí)驗(yàn)裝置和實(shí)驗(yàn)流程

1.2.1 實(shí)驗(yàn)裝置

低溫污泥干燥實(shí)驗(yàn)臺(tái)主要由以下部件組成：環(huán)境模擬箱（C7-1500 E series） ， 溫度精度±0.3 ℃ ，濕度精度±3% ， 偉思富奇環(huán)境試驗(yàn)儀器（太倉(cāng)）有限公司；拉壓力傳感器（ PBOL -01 series ） ， 精度±0.1 g ， 上海眾精科技發(fā)展有限公司；數(shù)字信號(hào)稱重通訊模塊（HYRS -485 MODBUS）及 PC 電腦等。環(huán)境模擬箱用來(lái)控制干燥的溫度和空氣相對(duì)濕度，拉壓力傳感器用來(lái)測(cè)量污泥質(zhì)量，數(shù)字信號(hào)稱重通訊模塊用來(lái)實(shí)時(shí)記錄污泥質(zhì)量并輸入到電腦中。

1.2.2 實(shí)驗(yàn)流程

第一步，制作薄層污泥。將不同質(zhì)量（分別為40 ， 80 ， 120 g）的污泥分別裝入200 mm ×200 mm ×2 mm ， 200 mm ×200 mm ×4 mm ， 200 mm ×200 mm ×6 mm 的鋼板模型，成型后的薄層污泥質(zhì)量與密度保持不變，污泥厚度分別為2 ， 4 ， 6 mm 。

第二步，啟動(dòng)環(huán)境模擬箱。智能溫控器溫度設(shè)定到預(yù)設(shè)值（40 ， 50 ， 60℃） ， 相對(duì)濕度設(shè)定到預(yù)設(shè)值（30% ， 40% ， 50% ， 60%） ， 風(fēng)速設(shè)置為1.5 m/s 。當(dāng)環(huán)境模擬箱內(nèi)環(huán)境達(dá)到穩(wěn)定狀態(tài)后，將預(yù)先準(zhǔn)備好的試驗(yàn)原料放入進(jìn)行干燥。

第三步，實(shí)時(shí)采集數(shù)據(jù)。試驗(yàn)數(shù)據(jù)每10 min 自動(dòng)采集1次，每個(gè)試驗(yàn)重復(fù)3次。

1.3 數(shù)據(jù)收集

表1總結(jié)了從實(shí)驗(yàn)中收集到的共1023個(gè)實(shí)驗(yàn)數(shù)據(jù)的輸入和輸出變量。輸入變量分別為厚度、溫度、相對(duì)濕度和干燥時(shí)間，厚度參數(shù)為2 ， 4 ， 6 mm ， 溫度參數(shù)為40 ， 50 ， 60℃ ， 相對(duì)濕度參數(shù)為30% ， 40% ， 50% ， 60%。由于所設(shè)環(huán)境參數(shù)不同，污泥的干燥時(shí)間不同，最小是0 min ， 最大是620 min 。輸出變量為水分比，記為 MR（某一時(shí)刻的干基含水率（g/g）除以初始干基含水率）。為了建立模型，將數(shù)據(jù)隨機(jī)分為訓(xùn)練樣本和測(cè)試樣本，用訓(xùn)練樣本對(duì)薄層干燥模型和 BP 神經(jīng)網(wǎng)絡(luò)模型進(jìn)行訓(xùn)練，用測(cè)試樣本驗(yàn)證模型預(yù)測(cè)的準(zhǔn)確性和可靠性。

2 結(jié)果與討論

2.1 相對(duì)濕度和溫度對(duì)污泥干燥特性的影響

為了方便污泥干燥后進(jìn)行資源化和低碳化處理，同時(shí)進(jìn)一步降低處理成本，有研究認(rèn)為將污泥濕基含水率（濕污泥中的水質(zhì)量與濕污泥質(zhì)量的比值）保持在30%左右是有利的[19] ， 因此本文以污泥濕基含水率30%作為干燥最優(yōu)狀態(tài)進(jìn)行分析。

圖2為4 mm 厚度的污泥在不同溫度和相對(duì)濕度條件下水分比和干燥速率（單位時(shí)間去除的污泥水分量，g/（g·min ））的變化。從水分比變化規(guī)律圖（圖2）可以看出，當(dāng)污泥厚度為4 mm 時(shí)，在不同的干燥溫度（40 ， 50 ， 60℃）下，相對(duì)濕度從60%下降到30% ， 污泥的干燥時(shí)間分別減少48% ， 52% ， 48% ， 相對(duì)濕度30%時(shí)所用的干燥時(shí)間相比60%時(shí)約減少了一半。這是由于隨著干燥相對(duì)濕度降低，污泥帶走水分的能力逐漸加強(qiáng)，使干燥效率增大。干燥相對(duì)濕度是影響低溫干燥效率的重要因素，這與污泥在高溫干燥情況下污泥干燥速率不受空氣相對(duì)濕度的影響明顯不同[20-21]。

為了進(jìn)一步分析相對(duì)濕度的影響，從干燥速率變化規(guī)律圖（圖2）可以看出，在相同的厚度和溫度下，污泥的干燥速率隨著相對(duì)濕度的降低而增加，這一結(jié)果與 Ruiz 等[22]的發(fā)現(xiàn)一致。當(dāng)厚度為4 mm、溫度為40℃時(shí)，相對(duì)濕度從60%下降到30% ， 其最大干燥速率從0.0138 g/（g·min ）增加到0.0271 g/（g·min ）。從濕空氣的熱質(zhì)傳遞特性可以發(fā)現(xiàn)，當(dāng)空氣相對(duì)濕度降低時(shí)，其吸濕能力增強(qiáng)，使干燥速率增加，溫度越低，這種現(xiàn)象表現(xiàn)越明顯。所以在實(shí)際應(yīng)用中，通過(guò)降低空氣濕度能顯著提高干燥速率，減少干燥所用時(shí)間。

對(duì)比圖2所示的水分比變化規(guī)律可以發(fā)現(xiàn)，當(dāng)厚度為4 mm ， 相對(duì)濕度30% ， 40%時(shí)，從40℃升高到50℃ ， 干燥時(shí)間分別減少21% ， 20%;從50℃升高到60℃ ， 干燥時(shí)間分別減少17% ， 15%。在濕度為30%～60%下，溫度每升高10℃ ， 干燥時(shí)間減少約20%。這是由于干燥溫度升高，加快了水分遷移，污泥內(nèi)部傳熱驅(qū)動(dòng)力增大，干燥效率增大。為了進(jìn)一步分析溫度的影響，對(duì)比圖2所示的干燥速率變化規(guī)律可以發(fā)現(xiàn)，在相同的厚度和相對(duì)濕度條件下，污泥的干燥速率隨溫度的升高而增大。當(dāng)厚度為4 mm、相對(duì)濕度為30%時(shí)，溫度從40℃上升到60℃ ， 其最大干燥速率從0.0271 g/（ g·min ）增加到0.0391 g/（g·min ）。因?yàn)樵谙嗤母稍锖穸群拖鄬?duì)濕度下，濕空氣達(dá)到飽和狀態(tài)所需的水分隨著溫度的升高而增加，從而強(qiáng)化污泥表面自由水的蒸發(fā)作用，同時(shí)溫度增加也加快了污泥內(nèi)部水分子的擴(kuò)散遷移，因此干燥速率增加。

2.2 污泥厚度對(duì)干燥特性的影響

圖3為不同厚度污泥在溫度為50℃、相對(duì)濕度40%情況下水分比和干燥速率的變化。從圖3可以看出，污泥薄層厚度從6 mm 下降到2 mm ， 每下降2 mm 污泥干燥時(shí)間分別下降32% ， 38% ， 所需干燥時(shí)間約減少三分之一。這是因?yàn)槟鄬釉奖≡接欣谒謴膬?nèi)部向外遷移，達(dá)到一定含水率所需的時(shí)間就會(huì)越短。在實(shí)際應(yīng)用中，可通過(guò)翻堆、攪拌等達(dá)到薄層干燥的效果，從而提高干燥效率。

為了進(jìn)一步分析薄層厚度的影響，圖3給出了干燥速率隨水分比的變化關(guān)系。從圖3可以看出，不同薄層厚度情況下，薄層厚度越小，其最大干燥速率越大，薄層厚度從6 mm 下降到2 mm ， 其最大干燥速率從0.0183 g/（g·min ）增加到0.0554 g/（g·min ）。這是因?yàn)槲勰嘀械乃謴奈勰鄡?nèi)部向外擴(kuò)散，空氣中的熱量向污泥內(nèi)部傳遞，隨著污泥厚度的減小，傳質(zhì)和傳熱的路徑減小，阻力變小，所以污泥干燥速率增大。

2.3 薄層干燥數(shù)學(xué)模型

薄層干燥數(shù)學(xué)模型可用于描述和預(yù)測(cè)物料的干燥過(guò)程。污泥干燥過(guò)程涉及復(fù)雜的傳熱傳質(zhì)過(guò)程，目前尚未建立準(zhǔn)確的動(dòng)力學(xué)模型來(lái)描述污泥干燥過(guò)程。為探索描述污泥干燥過(guò)程的方法，對(duì)表2列出的常用的5種薄層干燥模型進(jìn)行了擬合效果比較。

為選出最符合污泥干燥的模型，需要進(jìn)行數(shù)據(jù)統(tǒng)計(jì)檢驗(yàn)，主要是依據(jù)相關(guān)擬合參數(shù)進(jìn)行判斷。在 ORIGIN 2019b 軟件中，使用非線性回歸技術(shù)對(duì)污泥干燥過(guò)程中水分比隨時(shí)間變化的曲線進(jìn)行擬合，確定待定參數(shù)。利用決定系數(shù)（ Coefficient of determi- nation）R2、卡方系數(shù)（ Chi-square ）χ2和均方根誤差（Root mean square error ） RMSE 來(lái)評(píng)價(jià)不同模型與實(shí)驗(yàn)結(jié)果的擬合情況，數(shù)學(xué)表達(dá)式如下[26]：

式中：MRexp ， i和MRpre ， i分別是實(shí)驗(yàn)和預(yù)測(cè)的污泥水分比；n 為觀察次數(shù)；z 為自由度。R2 越大，χ2和 RMSE 值越小，測(cè)試值與干燥模型的擬合度就越好[27] ， 模型的適用性就強(qiáng)。

以干燥溫度50℃、相對(duì)濕度30%的實(shí)驗(yàn)工況為例，利用決定系數(shù) R2、卡方系數(shù)χ2和均方根誤差 RMSE 的值來(lái)評(píng)價(jià)各個(gè)干燥模型對(duì)實(shí)驗(yàn)結(jié)果擬合程度的高低，結(jié)果如圖4所示。

由圖4可知，利用這5種干燥模型對(duì)干燥溫度50℃、相對(duì)濕度40%時(shí)不同厚度工況下污泥干燥過(guò)程中水分比隨時(shí)間變化的曲線進(jìn)行擬合，結(jié)果發(fā)現(xiàn)Midilli模型決定系數(shù)高、且卡方系數(shù)和 RMSE 均較小，表現(xiàn)出較好的擬合結(jié)果。Midilli模型的相關(guān)參數(shù)如下：厚度為2 mm 時(shí)，R2 =0. 99908 ， χ2=9.64E -5 ， RMSE =5.79E -4;厚度為4 mm 時(shí)，決定系數(shù) R2=0.99928 ， χ2=6.58E -5 ， RMSE =9.87E -4; 厚度為6 mm 時(shí)，決定系數(shù) R2 =0.99948 ， χ2=4.71E -5 ， RMSE =1.22E -4。用 ORIGIN 2019b 軟件對(duì)所有實(shí)驗(yàn)工況下污泥干燥曲線進(jìn)行擬合，由擬合的曲線得到各個(gè)干燥模型的擬合系數(shù)，各模型的決定系數(shù) R2、卡方系數(shù)χ2和均方根誤差 RMSE 的均值見(jiàn)表3。從表3可以看出，Midilli模型 R2最高、χ2和 RMSE 最小。因此，Midilli模型被認(rèn)為是擬合效果最好的模型。

2.4 基于 BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)污泥低溫干燥過(guò)程2.4.1 BP 神經(jīng)網(wǎng)絡(luò)

BP 神經(jīng)網(wǎng)絡(luò)又稱并行計(jì)算網(wǎng)絡(luò)，由輸入層、隱藏層、輸出層構(gòu)成。神經(jīng)網(wǎng)絡(luò)系統(tǒng)的信息輸入由輸入層的每個(gè)神經(jīng)元節(jié)點(diǎn)來(lái)負(fù)責(zé)完成，并通過(guò)權(quán)值的連接將其傳遞給隱藏層中的每個(gè)神經(jīng)元節(jié)點(diǎn)。然后隱藏層將信息傳遞給輸出層各個(gè)神經(jīng)元，經(jīng)過(guò)輸出層進(jìn)一步處理，完成訓(xùn)練過(guò)程中的信息正向傳播，最后輸出層負(fù)責(zé)將神經(jīng)網(wǎng)絡(luò)系統(tǒng)的計(jì)算結(jié)果輸出。當(dāng)輸出值與真實(shí)值存在誤差時(shí)，神經(jīng)網(wǎng)絡(luò)系統(tǒng)進(jìn)入誤差反向傳播階段，神經(jīng)網(wǎng)絡(luò)系統(tǒng)計(jì)算總誤差，并通過(guò)誤差梯度下降方法從輸出層到輸入層反向調(diào)整各層的權(quán)重和閾值。

隱層神經(jīng)元的數(shù)量是需要考慮的重要參數(shù)之一。如果使用少量的隱藏層神經(jīng)元，網(wǎng)絡(luò)就無(wú)法進(jìn)行良好的預(yù)測(cè)。相反，冗余的隱層神經(jīng)元會(huì)導(dǎo)致過(guò)擬合。根據(jù) Piotrowski 等[28]的研究，選擇 Levenberg -Marquardt 訓(xùn)練（Trainlm ）算法和貝葉斯正則化訓(xùn)練（Trainbr ）算法進(jìn)行計(jì)算。上述算法均可在 MATLAB 軟件上實(shí)現(xiàn)。

2.4.2 優(yōu)化建模

Levenberg - Marquardt 訓(xùn)練（ Trainlm ）算法和貝葉斯正則化訓(xùn)練（Trainbr ）算法都具有較好的性能。Trainlm算法是應(yīng)用最廣泛的非線性最小二乘算法，它結(jié)合了最速下降法和線性化法。當(dāng)參數(shù)較小時(shí)，Trainbr算法通過(guò)修改損失函數(shù)來(lái)避免過(guò)擬合。圖5 顯示了Trainlm和Trainbr算法訓(xùn)練不同數(shù)量隱藏神經(jīng)元后測(cè)試數(shù)據(jù)的最大絕對(duì)誤差（Mean ab solute er- ror ， MAE）。從圖5可以看出，無(wú)論使用多少個(gè)隱藏神經(jīng)元，Trainlm算法得到的 MAE 值都要比Trainbr算法大得多，意味著Trainbr算法是 BP 神經(jīng)網(wǎng)絡(luò)的最佳選擇。此外，對(duì)于Trainlm算法訓(xùn)練的模型，測(cè)試樣本的 MAE 值幾乎是隨機(jī)的。出現(xiàn)這種不規(guī)則結(jié)果的原因被認(rèn)為是Trainlm算法在迭代過(guò)程中容易陷入局部最優(yōu)解，特別是當(dāng)維數(shù)非常大的時(shí)候。與Trainlm算法相比，當(dāng)隱藏神經(jīng)元個(gè)數(shù)大于30時(shí)，Trainbr算法訓(xùn)練的結(jié)果更穩(wěn)定。

圖6為Trainbr算法訓(xùn)練的大量擴(kuò)展隱藏神經(jīng)元的測(cè)試數(shù)據(jù)的 MAE 值。從圖6可以看出，當(dāng)隱藏神經(jīng)元數(shù)量進(jìn)一步增加時(shí)，Trainbr算法的 MAE 值會(huì)突然增加，當(dāng)隱藏神經(jīng)元個(gè)數(shù)低于44時(shí)，MAE 值幾乎沒(méi)有變化。因此，本文的 BP 神經(jīng)網(wǎng)絡(luò)模型中隱藏的神經(jīng)元數(shù)量確定為30個(gè)。

2.4.3 模型驗(yàn)證

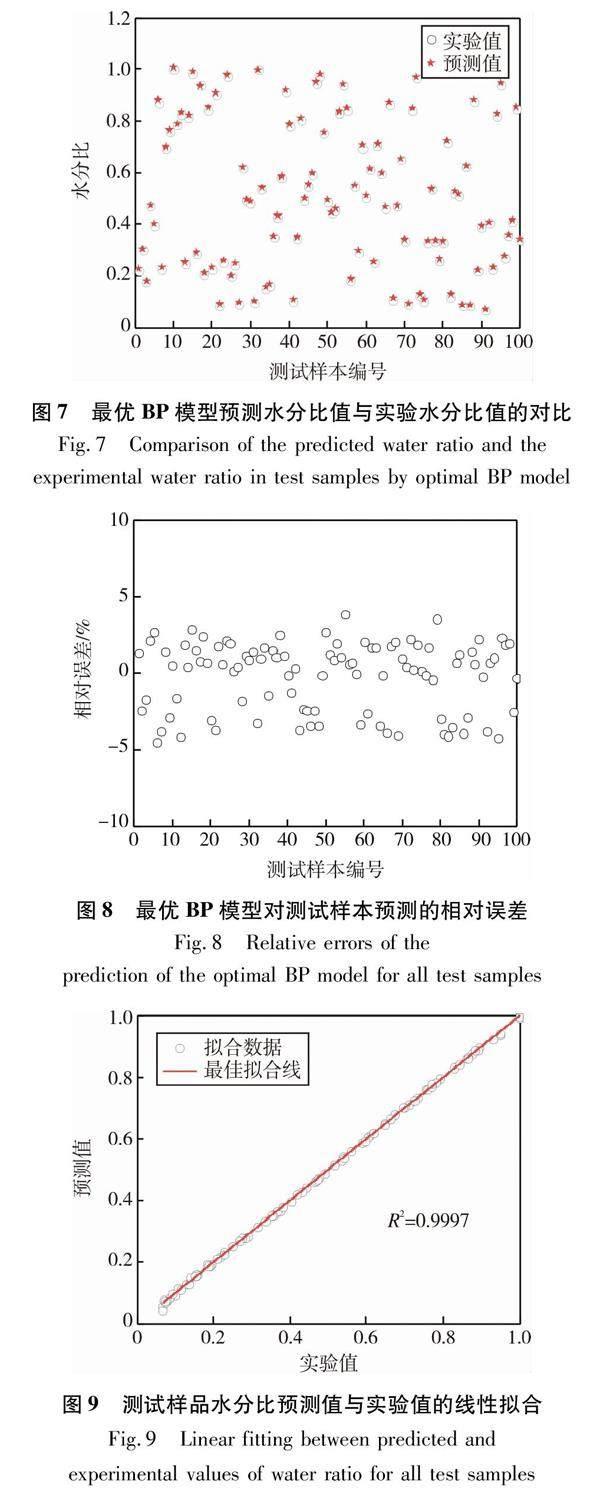
利用優(yōu)化后的 BP 神經(jīng)網(wǎng)絡(luò)模型，將預(yù)測(cè)的水分比與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比。圖7為最優(yōu) BP 模型在測(cè)試樣品中預(yù)測(cè)水分比值與實(shí)驗(yàn)水分比值的對(duì)比圖。從圖7可以看出，BP 神經(jīng)網(wǎng)絡(luò)模型預(yù)測(cè)的水分比值接近實(shí)驗(yàn)數(shù)據(jù)的水分比值。圖8為最優(yōu) BP 模型對(duì)所有測(cè)試樣本預(yù)測(cè)的相對(duì)誤差圖。從圖8可以看出，大部分的預(yù)測(cè)相對(duì)誤差（預(yù)測(cè)值與實(shí)驗(yàn)值之差／實(shí)驗(yàn)值）小于3% ， 所有預(yù)測(cè)的相對(duì)誤差均小于5%。圖9為所有測(cè)試樣品水分比預(yù)測(cè)值與實(shí)驗(yàn)值的線性擬合圖。從圖9可以看出，水分比預(yù)測(cè)值與實(shí)測(cè)數(shù)據(jù)具有很好的相關(guān)性（ R2 =0.9997）。以上結(jié)果表明所建立的 BP 模型具有很好的預(yù)測(cè)效果。

2.5 BP 神經(jīng)網(wǎng)絡(luò)模型與Midilli模型的預(yù)測(cè)精度比較

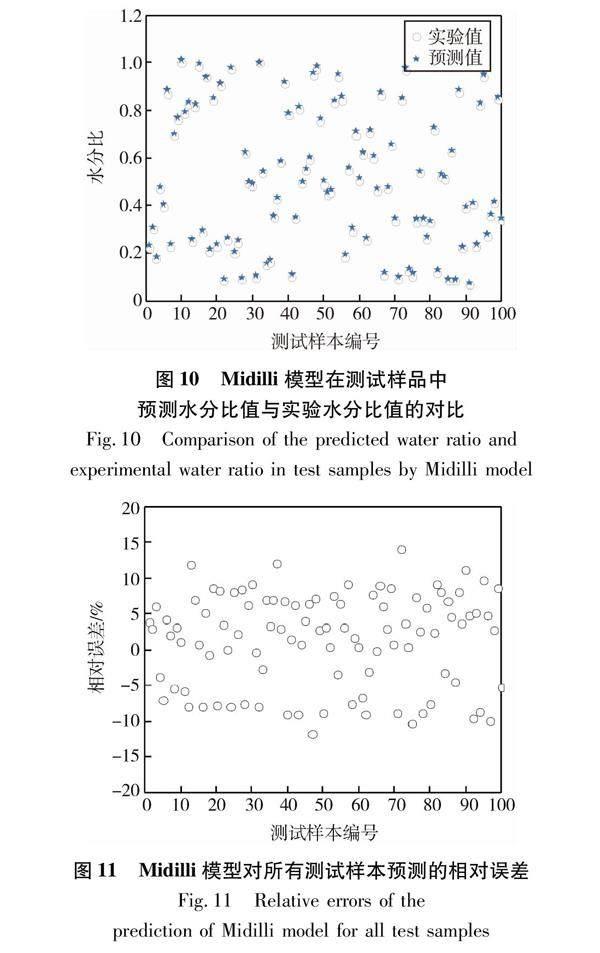
通過(guò)模型預(yù)測(cè)的水分比與實(shí)驗(yàn)水分比的比較及模型對(duì)所有測(cè)試樣本預(yù)測(cè)的相對(duì)誤差的比較，可以看出預(yù)測(cè)模型的預(yù)測(cè)精度。圖10為Midilli模型在測(cè)試樣品中預(yù)測(cè)水分比值與實(shí)驗(yàn)水分比值的對(duì)比圖。比較圖10與圖7可以看出，Midilli模型與 BP 模型相比，其預(yù)測(cè)水分比值與試驗(yàn)水分比值偏離更大。圖11為Midilli模型對(duì)所有測(cè)試樣本預(yù)測(cè)的相對(duì)誤差圖。從圖11可以看出，大部分的預(yù)測(cè)相對(duì)誤差都大于5% ， 甚至有些預(yù)測(cè)相對(duì)誤差超過(guò)10% ， 而 BP 模型大部分的預(yù)測(cè)相對(duì)誤差小于3% ， 所有預(yù)測(cè)的相對(duì)誤差均小于5%（圖8）。所以，BP 神經(jīng)網(wǎng)絡(luò)模型預(yù)測(cè)污泥低溫干燥過(guò)程的精確度比Midilli模型更高。這是由于 BP 神經(jīng)網(wǎng)絡(luò)模型不涉及過(guò)程的內(nèi)部機(jī)制，只要有大量的數(shù)據(jù)對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，網(wǎng)絡(luò)就能找出輸入輸出關(guān)系，建立精確的數(shù)學(xué)模型。因此，BP 神經(jīng)網(wǎng)絡(luò)模型更適合污泥干燥過(guò)程的預(yù)測(cè)。

3 結(jié)論

以綿陽(yáng)地區(qū)市政污泥為研究對(duì)象，搭建了污泥干燥測(cè)試實(shí)驗(yàn)平臺(tái)，分析了污泥低溫干燥過(guò)程的影響因素，并以實(shí)驗(yàn)結(jié)果為數(shù)據(jù)源，以污泥干燥溫度、相對(duì)濕度、污泥厚度、污泥干燥時(shí)間為輸入量，水分比為輸出量，建立了污泥干燥預(yù)測(cè)模型。結(jié)論如下：（1）低溫干燥時(shí)，污泥水分比的變化除受干燥溫度影響外，還受干燥環(huán)境空氣相對(duì)濕度的影響。在一定條件下，相對(duì)濕度從60%降到30% ， 可以減少約一半的干燥時(shí)間；空氣溫度每上升10℃可以減少約20%的干燥時(shí)間；污泥薄層厚度每下降2 mm 可以減少1/3的干燥時(shí)間。（2）在污泥干燥各工況下，Midilli模型決定系數(shù)最高，且卡方系數(shù)和均方根誤差最小，Midilli模型是薄層干燥模型中擬合效果最好的模型。（3）在 BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型中，貝葉斯正則化訓(xùn)練（ Trainbr ）算法提供了比 Levenberg -Marquardt 訓(xùn)練（ Trainlm ）算法更好的訓(xùn)練結(jié)果，本研究中隱藏神經(jīng)元的最佳數(shù)量為30個(gè)。（4）相比Midilli模型的預(yù)測(cè)結(jié)果，BP 神經(jīng)網(wǎng)絡(luò)模型預(yù)測(cè)結(jié)果與實(shí)驗(yàn)結(jié)果的相對(duì)誤差均小于5% ， 具有更好的預(yù)測(cè)精度。

參考文獻(xiàn)

[1] VAXELAIRE J ， C？ZAC P. Moisture distribution in acti- vated sludges ： a review [ J ]. Water Research ， 2004 ， 38（9）：2215-2230.

[2] ZHANG Q H ， YANG W N ， NGO H H ， et al. Current status of urban wastewater treatment plants in China [ J]. Environment International ， 2016 ， 92/93：11-22.

[3] TUNCAL T ， USLU O . A review of dehydration of various industrial sludges [ J]. Drying Technology Drying Tech- nology ， 2014 ， 32（14）：1642-1654.

[4] WU B R ， DAI X H ， CHAI X L. Critical review on dewatering of sewage sludge ： influential mechanism ， conditioning technologies and implications to sludge re-utilizations [J]. Water Research ， 2020 ， 180：115912.

[5] BOGLER A ， PACKMAN A ， FURMAN A ， et al. Rethinking wastewater risks and monitoring in light of the COVID-19 pandemic [J]. Nature Sustainability ， 2020 ， 3（12）：981-990.

[6] BENNAMOUN L ， ARLABOSSE P ， L？ONARD A. Re- view on fundamental aspect of application of dryingprocess to wastewater sludge [J]. Renewable and Sustain- able Energy Reviews ， 2013 ， 28：29-43.

[7] ZHAO L J ， YANG J H ， WANG S S ， et al. CO-drying characteristics of sticky sewage sludge pre-conditioned with biomass and coal [ J]. Drying Technology ， 2020 ， 38（15）：2083-2093.

[8] WANG T ， XUE Y J ， HAO R ， et al. Mechanism investi- gations into the effect of rice husk and wood sawdust con- ditioning on sewage sludge thermal drying[J]. Journal of Environmental Management ， 2019 ， 239：316-323.

[9] L？ONARD A ， VANDEVENNE P ， SALMON T ， et al. Waste water sludge convective drying： influence of sludge origin [ J ]. Environmental Technology Letters ， 2004 ， 25（9）：1051-1057.

[10] MOU X Z ， CHEN Z Q. Experimental study on the effect of sludge thickness on the characteristics of ultrasound-assisted hot air convective drying municipal sewage sludge [ J ]. Drying Technology ， 2021 ， 39（6）：752-764.

[11] L？ONARD A ， MENESES E ， LE TRONG E ， et al. Influ- ence of back mixing on the convective drying of residual sludges in a fixed bed [ J ]. Water Research ， 2008 ， 42（10/11）：2671-2677.

[12] HENDERSON S M ， PABIS S . Grain drying theory ， II . Temperature effects on drying coefficients [ J]. Journal of Agricultural Engineering Research ， 1961 ， 6：169-174.

[13] MIDILLI A ， KUCUK H ， YAPAR Z . A new model forsingle-layer drying[J]. Drying Technology ， 2002 ， 20（7）：1503-1513.

[14] GHAZANFARI A ， EMAMI S ， TABIL L G ， et al. Thin- layer drying of flax fiber ： II . Modeling drying process using semi-theoretical and empirical models [ J]. Drying Technology ， 2006 ， 24（12）：1637-1642.

[15] CORZO O ， BRACHO N ， PEREIRA A ， et al. Weibull distribution for modeling air drying of coroba slices [ J]. LWT - Food Science and Technology ， 2008 ， 41（10）：2023-2028.

[16]伍丹華，周禮梅．基于 BP 神經(jīng)網(wǎng)絡(luò)的糧食產(chǎn)量預(yù)測(cè)[J].農(nóng)業(yè)工程技術(shù)，2020 ， 40（27）：51-53.

[17]張利娟，耿令新，金鑫，等．基于 BP 神經(jīng)網(wǎng)絡(luò)的小麥真空干燥含水率預(yù)測(cè)模型[ J].河南工業(yè)大學(xué)學(xué)報(bào)（自然科學(xué)版），2016 ， 37（3）：101-106.

[18] HAN Y ， YAN S ， SUN Y ， et al. Modeling the constitutive relationship of Al -0.62Mg -0.73Si alloy based on artifi- cial neural network[J]. Metals ， 2017 ， 7（4）：114.

[19] SEGGIANI M ， VITOLO S ， PUCCINI M ， et al. C ogasifi-cation of sewage sludge in an updraft gasifier [ J]. Fuel ， 2012 ， 93：486-491.

[20] ZHENG Q S ， HU Z Y ， LI P G ， et al. Effects of air pa- rameters on sewage sludge drying characteristics and re- gression analyses of drying model coefficients [ J]. Ap- plied Thermal Engineering ， 2021 ， 198：117501.

[21] RAMACHANDRAN R P ， PALIWAL J ， CENKOWSKI S . Modeling of effective moisture diffusivity and activation energy of distillers spent grain pellets with solubles dur- ing superheated steam drying[ J]. Biomass and Bioener- gy ， 2018 ， 116：39-48.

[22] RUIZ T ， WISNIEWSKI C . C orrelation between dewate- ring and hydro-textural characteristics of sewage sludgeduringdrying[ J]. Separation and Purification Technolo- gy ， 2008 ， 61（2）：204-210.

[23] PAGE G E . Factors influencing the maximum rates of air drying shelled corn in thin layers [D]. Thesis ， Purdue U- niversity ， West Lafayette ， 1949.

[24] TOGRUL T ， PEHLIVAN D . Mathematical modelling of solar drying of apricots in thin layers [J]. Journal of Food Engineering ， 2002 ， 55（3）：209-216.

[25] DANISH M ， HU J ， ZHOU P ， et al. A new drying kinetic model for sewage sludge drying in presence of C aO and NaClO[ J ]. Applied Thermal Engineering ， 2016 ， 106：141-152.

[26] JANJAI S ， PRECOPPE M ， LAMLERT N ， et al. Thin- layer drying of litchi （Litchi chinensis Sonn.）[J]. Food and Bioproducts Processing ， 2011 ， 89（3）：194-201.

[27] DOYMAZ I. Drying kinetics ， rehydration and colourcharac- teristics of convective hot-air drying of carrot slices [ J]. Heat and Mass Transfer ， 2017 ， 53（1）：25-35.

[28] PIOTROWSKI A P ， NAPIORKOWSKI J J. A comparison of methods to avoid overfitting in neural networks training in the case of catchment runoff modelling[ J]. Journal of Hydrology ， 2013 ， 476：97-111.