循環(huán)加載下壓實(shí)黃土的邊界面塑性本構(gòu)模型

代倩 廖紅建 康孝森 孫玉軍 周恒

收稿日期：2023-10-15

基金項(xiàng)目：陜西省教育廳科研計(jì)劃項(xiàng)目（22JK0445）；陜西省秦創(chuàng)原“科學(xué)家+工程師”隊(duì)伍建設(shè)項(xiàng)目（2023KXJ-178）。

第一作者：代倩，女，博士生，從事黃土動(dòng)力學(xué)試驗(yàn)與數(shù)值模擬等研究，daiqian68@stu.xjtu.edu.cn。

通信作者：廖紅建，女，博士，教授，從事巖土本構(gòu)關(guān)系、巖土工程減災(zāi)與防災(zāi)等研究，hjliao@mail.xjtu.edu.cn。

摘要? 壓實(shí)黃土的動(dòng)應(yīng)力應(yīng)變關(guān)系預(yù)測(cè)是黃土高原平山填方工程長(zhǎng)期運(yùn)營(yíng)涉及的關(guān)鍵問題之一，已有模型預(yù)測(cè)壓實(shí)黃土的動(dòng)本構(gòu)關(guān)系難度較大。該文在邊界面塑性框架下，引入動(dòng)態(tài)映射法則，提出了一個(gè)反映應(yīng)變累積的循環(huán)加載塑性模量表達(dá)式，構(gòu)建了循環(huán)加載條件下壓實(shí)黃土邊界面塑性本構(gòu)模型，分析了循環(huán)應(yīng)力比與圍壓對(duì)應(yīng)力應(yīng)變關(guān)系與模量的影響規(guī)律，采用壓實(shí)粉質(zhì)黃土動(dòng)三軸試驗(yàn)結(jié)果進(jìn)行了驗(yàn)證。結(jié)果表明，該循環(huán)加載塑性模量基本反映了壓實(shí)黃土的應(yīng)變累積行為，所構(gòu)建的本構(gòu)模型考慮了循環(huán)應(yīng)力比對(duì)動(dòng)應(yīng)力應(yīng)變關(guān)系與模量的影響，可為填方壓實(shí)黃土長(zhǎng)期變形分析提供參考。

關(guān)鍵詞? 壓實(shí)黃土;循環(huán)加載;應(yīng)力應(yīng)變;本構(gòu)模型;塑性模量

中圖分類號(hào)： TU473? DOI：10.16152/j.cnki.xdxbzr.2024-01-004

Bounding surface plasticity model of compactedloess under cyclic loading

DAI Qian1，2，? LIAO Hongjian1，2， KANG Xiaosen3， SUN Yujun4， ZHOU Heng5

（1.School of Human Settlements and? Civil Engineering， Xian Jiaotong University， Xian 710049， China;

2.School of Civil Engineering，?? Xian Jiaotong University City College， Xian 710018， China;

3.School of Geological Engineering and Geomatics， Changan University， Xian 710064， China;

4.State Power Investment Corporation， Yellow River Upper Reaches Hydropower Development Co.， Ltd.， Xining 810001，? China；

5.Powerchina Northwest Engineering Co.， Ltd.， Xian 710065， China）

Abstract? The prediction of the dynamic stress-strain relationship of compacted loess is essential in the projects of gully reclamation for farming and cutting mountains for city building in Loess Plateau. It is still difficult to predict the behaviors. To fill the gap， this paper formulates a bounding surface plasticity model for compacted loess subjected to cyclic loading. Specifically， a plastic modulus for cyclic loading is proposed to reflect the behaviors of? accumulated strain， and an updated mapping rule is introduced. Furthermore， the influence of confining pressure and cyclic stress ratio on stress-strain relationship and modulus is shown by several case studies， which is verified by experimental tests of compacted loess. The results show that the plastic modulus reflects? accumulated strain of compacted loess.The constitutive model considers the effect of cyclic stress ratio on dynamic stress-strain relationship and modulus of compacted loess because of the proposed plastic modulus and updated mapping rule. The results can give reference for analysis of long-term deformation of loess-filled foundation.

Keywords? compacted loess; cyclic loading; stress-strain; constitutive model; plastic modulus

黃土地區(qū)平山造城、 治溝造地、 高速鐵路等工程涉及不同規(guī)模的填方壓實(shí)黃土（見圖1）， 長(zhǎng)期循環(huán)荷載下壓實(shí)黃土產(chǎn)生累積變形，準(zhǔn)確預(yù)測(cè)壓實(shí)黃土的循環(huán)加載累積變形對(duì)于陜西、 山西及甘肅等地區(qū)的黃土填方工程運(yùn)營(yíng)具有重要的實(shí)際意義。

目前，循環(huán)加載條件下砂土與黏土本構(gòu)模型研究較為廣泛和深入。砂土模型一般采用錐面屈服面，基于記憶面［1］或邊界面等［2］構(gòu)建砂土循環(huán)加載本構(gòu)模型［3-4］，考慮相變狀態(tài)參量［5］、組構(gòu)演化［6］及非共軸特性［7］等。黏土循環(huán)加載本構(gòu)模型一般采用修正劍橋模型屈服面，基于邊界面塑性，采用映射法則與塑性模量反映循環(huán)加載過程中的塑性應(yīng)變累積［8-9］，求解復(fù)雜動(dòng)力邊值問題［10］。還將非飽和土水力特性引入邊界面塑性框架，建立了熱水力耦合模型［11］，以及考慮非飽和狀態(tài)參量和顆粒破碎參數(shù)［12］及損傷特性［13］。而黃土循環(huán)加載本構(gòu)模擬研究較少，已有研究主要是單調(diào)加載下黃土的損傷特性［14-15］、各向異性［16］、結(jié)構(gòu)性［17-18］、臨界狀態(tài)線不唯一［19］等。可借鑒以往黏土本構(gòu)模型構(gòu)建黃土的循環(huán)加載本構(gòu)模型，崔廣芹在邊界面塑性框架下研究了黃土的動(dòng)本構(gòu)模型［20］。在土的動(dòng)本構(gòu)模型中，映射中心與塑性模量關(guān)系到加載過程中塑性應(yīng)變累積，映射中心可能沿應(yīng)力加載方向運(yùn)動(dòng)［21］。塑性模量影響循環(huán)加載條件下黃土偏應(yīng)變累積穩(wěn)定與非穩(wěn)定狀態(tài)，合適的循環(huán)加載塑性模量對(duì)預(yù)測(cè)壓實(shí)黃土動(dòng)力特性至關(guān)重要［10，22］。

雖然上述學(xué)者開展了黃土動(dòng)本構(gòu)模型的研究，但模型尚未考慮到黃土的臨界狀態(tài)線不唯一的基本特性，尤其是粉質(zhì)黃土中粉粒組含量高，屬于間隔級(jí)配土一類，且大孔隙架空結(jié)構(gòu)導(dǎo)致其初始孔隙比范圍較大，臨界狀態(tài)線明顯依賴于初始孔隙比［19，23］。而臨界狀態(tài)線對(duì)于循環(huán)加載下黃土的動(dòng)力行為預(yù)測(cè)至關(guān)重要，循環(huán)加載下黃土的本構(gòu)關(guān)系預(yù)測(cè)仍然是一個(gè)挑戰(zhàn)。本文在邊界面塑性理論框架下，基于Kang等建立的邊界面塑性本構(gòu)模型［24］，引入動(dòng)態(tài)映射法則，提出一個(gè)循環(huán)加載條件下壓實(shí)黃土塑性模量表達(dá)式，推導(dǎo)壓實(shí)黃土動(dòng)本構(gòu)模型，模擬不同循環(huán)應(yīng)力比時(shí)壓實(shí)黃土動(dòng)本構(gòu)關(guān)系。研究結(jié)果可為填方黃土變形分析提供參考。

1? 本構(gòu)模型

1.1? 考慮黃土臨界壓力比的邊界面

傳統(tǒng)各向異性邊界面不能反映黃土的臨界狀態(tài)線不唯一性［19，23］，可通過臨界壓力比這一指標(biāo)反映（見圖1），故采用考慮臨界壓力比的邊界面［24］，

[AKf-]=（[AKq-D]-[AKp-D]′α）2+[AKM-]2[AKp-D]′（[AKp-D]′-[AKp-D]′0）=0? [JY]（1）

式中：（[AKp-D]′，[AKq-D]）為各向異性結(jié)構(gòu)性邊界面上的像應(yīng)力;α為各向異性不變量;p′[TX-]0為等向硬化參數(shù);[AKM-]由下式確定。

[AKM-]=（+（1-）[AKp-D]′[AKp-D]′0-1）[KF（]M2-α2[KF）]? [JY]（2）

式中：M為不同洛德角時(shí)臨界狀態(tài)線斜率，M=gθMc;由下式確定［24］。

=[KF（][SX（]M-αc[]M+αc[SX）][KF）][SX（]r[]（r-1）32[SX）]-[SX（]1[]r-1[SX）]? [JY]（3）

式中：αc為臨界狀態(tài)時(shí)α的值，臨界壓力比r反映臨界狀態(tài)線與等向壓縮線的距離。

1.2? 加載面與塑性勢(shì)面

對(duì)于超固結(jié)土，初始時(shí)加載面在邊界面內(nèi)，破壞時(shí)加載面與邊界面一致，加載面為［24］

[AKf-]=（q-p′α）2+[AKM-]2p′（p′-p′0）=0? [JY]（4）

式中：（p′，q）為當(dāng)前應(yīng)力，位于加載面上。循環(huán)加載過程加載面與邊界面相似，相似中心為反轉(zhuǎn)應(yīng)力點(diǎn)。

塑性勢(shì)函數(shù)［24］

g=（[AKq-D]-[AKp-D]′α）2+M2[AKp-D]′（[AKp-D]′-[AKp-D]′g）? [JY]（5）

式中：[AKp-D]′g反映塑性勢(shì)面大小。

1.3? 等向硬化與旋轉(zhuǎn)硬化

等向硬化采用修正劍橋模型硬化法則，

d[AKp-D]′0=〈L〉[SX（][AKp-D]′0[]Cp[SX）][SX（]g[][AKp-D]′[SX）]? [JY]（6）

式中：Cp為λ-κ1+e0，λ與κ分別為壓縮線與等向加卸載線的斜率。

初始各向異性與誘發(fā)各向異性采用Dafalias與Taiebat提出的各向異性演化表達(dá)式［25］，

dα=〈L〉crpa（αb-α）[SX（][AKp-D]′[][AKp-D]′0[SX）]? [JY]（7）

式中： pa為標(biāo)準(zhǔn)大氣壓; cr為常數(shù)， 控制各向異性結(jié)構(gòu)性邊界面q軸方向的旋轉(zhuǎn)率。 〈·〉為Maca-uley算子。αb為各向異性不變量α的上限值，表達(dá)式為［25］

αb=±[SX（]M[]ζ[SX）]（1-eζ|η|M）? [JY]（8）

式中：ζ為控制參數(shù)。

1.4? 循環(huán)加載映射法則

邊界面塑性框架下，預(yù)測(cè)循環(huán)加載條件下應(yīng)變累積，需采用更新映射中心法則［26］，循環(huán)加載條件下，映射中心從上一個(gè)應(yīng)力反轉(zhuǎn)點(diǎn)更新至下一個(gè)應(yīng)力反轉(zhuǎn)點(diǎn)（見圖2）。壓實(shí)黃土首次加載與后續(xù)循環(huán)加卸載所產(chǎn)生的累積應(yīng)變規(guī)律不同，首次加載時(shí)累積應(yīng)變顯著大于后續(xù)循環(huán)加載一次時(shí)應(yīng)變累積。

首次加載時(shí)映射中心設(shè)為原點(diǎn)，單調(diào)加載本構(gòu)模型亦設(shè)原點(diǎn)為映射中心，后續(xù)循環(huán)加載時(shí)映射中心設(shè)定為應(yīng)力反轉(zhuǎn)點(diǎn)，已廣泛應(yīng)用于循環(huán)加載本構(gòu)模型中。采用Seidalinov與Taiebat所提出的更新映射法則［27］如下，

[AKp-D]′=p′mc+ρ（p′-p′mc）

[AKq-D]=qmc+ρ（q-qmc）[JY]（9）

式中：ρ為相似比;（p′mc，qmc）為映射中心的應(yīng)力狀態(tài)。將像應(yīng)力代入邊界面表達(dá)式中即可求得相似比ρ，算得當(dāng)前應(yīng)力與像應(yīng)力在應(yīng)力空間的距離，確定循環(huán)加卸載中塑性模量值。

1.5? 循環(huán)加載塑性模量

塑性模量是邊界面塑性理論最為重要的一部分，直接關(guān)系到塑性變形累積計(jì)算的準(zhǔn)確性。在邊界面塑性框架下，塑性模量Kbδ=Kb+Kδ。Kb為各向異性結(jié)構(gòu)性邊界面上像應(yīng)力相關(guān)的塑性模量分量，由各向異性結(jié)構(gòu)性邊界面一致性條件確定，而經(jīng)典塑性理論只有Kb這一項(xiàng)，只能反映應(yīng)力狀態(tài)達(dá)到屈服面時(shí)塑性應(yīng)變，不能反映壓實(shí)黃土初始塑性應(yīng)變累積與循環(huán)加載塑性應(yīng)變累積效應(yīng)。Kδ為當(dāng)前應(yīng)力狀態(tài)相關(guān)的塑性模量分量，由當(dāng)前應(yīng)力與像應(yīng)力在應(yīng)力空間中坐標(biāo)決定。

基于Seidalinov與Taiebat［26］的塑性模量公式，考慮循環(huán)加載下壓實(shí)黃土變形規(guī)律，提出一個(gè)改進(jìn)循環(huán)加載塑性模量Kδ，

Kδ=[AKp-D]′04（ρ-1）2e-ad∫[SX（]1[]ε0[SX）]|Δεpq |? [JY]（10）

式中：ad為塑性模量衰減參數(shù);ε0為參考應(yīng)變值0.15;Δεpq為塑性偏應(yīng)變?cè)隽俊?/p>

循環(huán)加載條件下，當(dāng)ad越大，Kδ衰減越快，反映隨著塑性應(yīng)變累積過程中壓實(shí)黃土更容易破壞。

（ρ-1）2反映當(dāng)前應(yīng)力狀態(tài)相關(guān)的塑性模量Kb大小與當(dāng)前應(yīng)力和像應(yīng)力在應(yīng)力空間中的距離密切相關(guān)。若當(dāng)前應(yīng)力遠(yuǎn)離像應(yīng)力，如當(dāng)前應(yīng)力接近映射中心，則（ρ-1）2達(dá)到較大值，則Kδ較大，塑性應(yīng)變累積極小，接近彈性狀態(tài)。若當(dāng)前應(yīng)力逐漸接近像應(yīng)力，例如當(dāng)前應(yīng)力在映射中心與像應(yīng)力中間時(shí)，則（ρ-1）2逐漸接近0，Kδ逐漸接近0，塑性應(yīng)變累積率逐漸增大，表現(xiàn)為材料由彈性狀態(tài)向彈塑性狀態(tài)過渡。當(dāng)前應(yīng)力與像應(yīng)力相等時(shí)，則（ρ-1）2為0，Kδ為0，塑性應(yīng)變累積率達(dá)到最大，表現(xiàn)為材料彈塑性狀態(tài)，這一狀態(tài)與經(jīng)典塑性力學(xué)彈塑性狀態(tài)一致。

由邊界面式（1）的一致性條件，推導(dǎo)得塑性模量Kb表達(dá)式為

Kb=cpa（α-αb）[SX（][AKp-D]′[][AKp-D]′0[SX）][SX（][AKf-][]α[SX）]-[SX（][AKp-D]′0[]Cp[SX）][SX（]g[][AKp-D]′[SX）][SX（][AKf-][][AKp-D]′0[SX）]? [JY]（11）

1.6? 應(yīng)力應(yīng)變關(guān)系

根據(jù)非關(guān)聯(lián)流動(dòng)法則，

dεp=〈L〉[SX（]g[][AKσ-D][SX）]? [JY]（12）

式中：塑性乘子表達(dá)為

L=[SX（]1[]Kbδ[SX）][JB（（][SX（]f[][AKσ-D][SX）]：d[AKσ-D][JB））]? [JY]（13）

根據(jù)廣義胡克定律，

dσ=Dedεe? [JY]（14）

式中：為De彈性矩陣。

由應(yīng)變可加性計(jì)算總應(yīng)變?cè)隽浚?/p>

dε=dεe+dεp? [JY]（15）

由上述表達(dá)式及一致性條件，得增量型應(yīng)力應(yīng)變關(guān)系為

dσ=Depdεe? [JY]（16）

式中：彈塑性剛度矩陣為

Dep=De-（Kbδ+nDem）-1DemnDe [JY]（17）

式中：m和n分別為

m=（g／[AKσ-D]）／‖g／[AKσ-D]‖? [JY]（18）

n=（[AKf-]／[AKσ-D]）／‖[AKf-]／[AKσ-D]‖? [JY]（19）

2? 算例分析

2.1? 模型參數(shù)

模型含10個(gè)材料參數(shù)，通過常規(guī)三軸試驗(yàn)、循環(huán)加載試驗(yàn)及試算確定。①?gòu)?qiáng)度參數(shù)：黏聚力c，斜率Mc為常規(guī)三軸壓縮路徑下臨界狀態(tài)線的斜率，Me為常規(guī)三軸拉伸路徑下臨界狀態(tài)線的斜率，通過常規(guī)三軸試驗(yàn)即可確定。②壓縮參數(shù)與回彈參數(shù)：λ和κ分別為v-ln p′平面上等向壓縮線斜率與卸載加載線斜率，通過等向壓縮試驗(yàn)確定。③彈性參數(shù)：泊松比μ設(shè)為0.3。④臨界壓力比：r反映的是臨界狀態(tài)時(shí)有效平均主應(yīng)力p′與硬化參數(shù)p′0之間的關(guān)系，在v-ln p′平面上分析臨界狀態(tài)線與等向壓縮線確定（見圖1）。⑤旋轉(zhuǎn)硬化參數(shù)：cr控制邊界面旋轉(zhuǎn)，ζ反映了應(yīng)力路徑對(duì)旋轉(zhuǎn)硬化參數(shù)上限值的影響，通過試算確定［25］。⑥塑性模量參數(shù)：ad控制塑性模量增大或減小，根據(jù)循環(huán)加卸載試驗(yàn)應(yīng)變累積確定，若偏應(yīng)變穩(wěn)定于某一值且小于破壞應(yīng)變，則ad取正值;若偏應(yīng)變大于破壞應(yīng)變且不穩(wěn)定，則ad取負(fù)值。

2.2? 算例

通過循環(huán)加載算例分析不同循環(huán)應(yīng)力比條件下應(yīng)力應(yīng)變滯回圈、循環(huán)加載非線性、動(dòng)楊氏模量的變化規(guī)律。材料參數(shù)值根據(jù)一般土性參數(shù)設(shè)定（見表1），結(jié)果見圖3。

由圖3（a）可知，循環(huán)加載過程中應(yīng)力應(yīng)變曲線非線性，應(yīng)力應(yīng)變滯回圈逐漸趨于穩(wěn)定，循環(huán)應(yīng)力比越大，滯回圈越顯著，反映了循環(huán)加載下黃土的彈塑性行為。進(jìn)一步，隨著循環(huán)次數(shù)的增加，累積塑性應(yīng)變?cè)龃螅兓吭絹碓叫。绕涫茄h(huán)應(yīng)力比CSR（σd／（2σc））越大，塑性應(yīng)變累積越快。

由圖3（b）可知，循環(huán)加載過程中動(dòng)楊氏模量逐步衰減，當(dāng)循環(huán)應(yīng)力比為常數(shù)，動(dòng)楊氏模量隨著塑性應(yīng)變累積而減小，當(dāng)累積塑性應(yīng)變?yōu)槟骋惶囟ㄖ担瑒?dòng)楊氏模量隨著循環(huán)應(yīng)力比增大而減小。該規(guī)律反映了循環(huán)加載過程中土結(jié)構(gòu)損傷演化與應(yīng)變累積和循環(huán)應(yīng)力比的相關(guān)性，循環(huán)應(yīng)力比較小引起結(jié)構(gòu)損傷較小，循環(huán)應(yīng)力比較大引起結(jié)構(gòu)損傷較大，符合循環(huán)加載下黃土變形規(guī)律。

3? 驗(yàn)證與討論

應(yīng)用該模型預(yù)測(cè)循環(huán)加載條件下飽和壓實(shí)黃土的動(dòng)應(yīng)力應(yīng)變關(guān)系、塑性應(yīng)變累積及動(dòng)楊氏模量衰減規(guī)律［27］。材料參數(shù)取值根據(jù)文獻(xiàn)［24］確定（見表2）。

由圖4、5可知，模型模擬了飽和壓實(shí)黃土的循環(huán)加載非線性及應(yīng)力應(yīng)變滯回效應(yīng)。首先，當(dāng)循環(huán)應(yīng)力比較大時(shí)，飽和黃土應(yīng)力狀態(tài)接近邊界面，應(yīng)力應(yīng)變表現(xiàn)出強(qiáng)非線性，軸向應(yīng)變累積顯著，且首次加載應(yīng)力應(yīng)變曲線與后續(xù)加載應(yīng)力應(yīng)變曲線顯著不同。模型通過引入更新映射中心法則，首次加載時(shí)映射中心為原點(diǎn)，后續(xù)加載時(shí)映射中心為應(yīng)力反轉(zhuǎn)點(diǎn)，較好模擬了飽和壓實(shí)黃土首次加載與后續(xù)加載應(yīng)力應(yīng)變關(guān)系。其次，飽和壓實(shí)黃土應(yīng)力應(yīng)變滯回效應(yīng)顯著，循環(huán)應(yīng)力比越大滯回圈愈大，且隨著加載次數(shù)增大逐漸趨于穩(wěn)定，模型較好地模擬了應(yīng)力應(yīng)變滯回圈疏密變化，經(jīng)典彈塑性模型難以實(shí)現(xiàn)。

由圖6可知，模型基本預(yù)測(cè)了飽和壓實(shí)黃土的塑性應(yīng)變累積行為。隨著循環(huán)次數(shù)的增大，累積軸向應(yīng)變?cè)龃螅S向應(yīng)變?cè)黾铀俾手饾u減小。循環(huán)應(yīng)力比越大，累積軸向應(yīng)變?cè)酱螅翗痈菀走_(dá)到破壞條件，如CSR=0.43對(duì)應(yīng)的軸向應(yīng)變遠(yuǎn)大于CSR=0.35對(duì)應(yīng)的軸向應(yīng)變（見圖6）。一方面，循環(huán)應(yīng)力比越大，應(yīng)力狀態(tài)越靠近邊界面，導(dǎo)致塑性模量較小且應(yīng)變?cè)隽枯^大，更易產(chǎn)生塑性應(yīng)變累積。另一方面，循環(huán)應(yīng)力比越大，應(yīng)力狀態(tài)更快到達(dá)臨界狀態(tài)線，更快達(dá)到破壞條件。

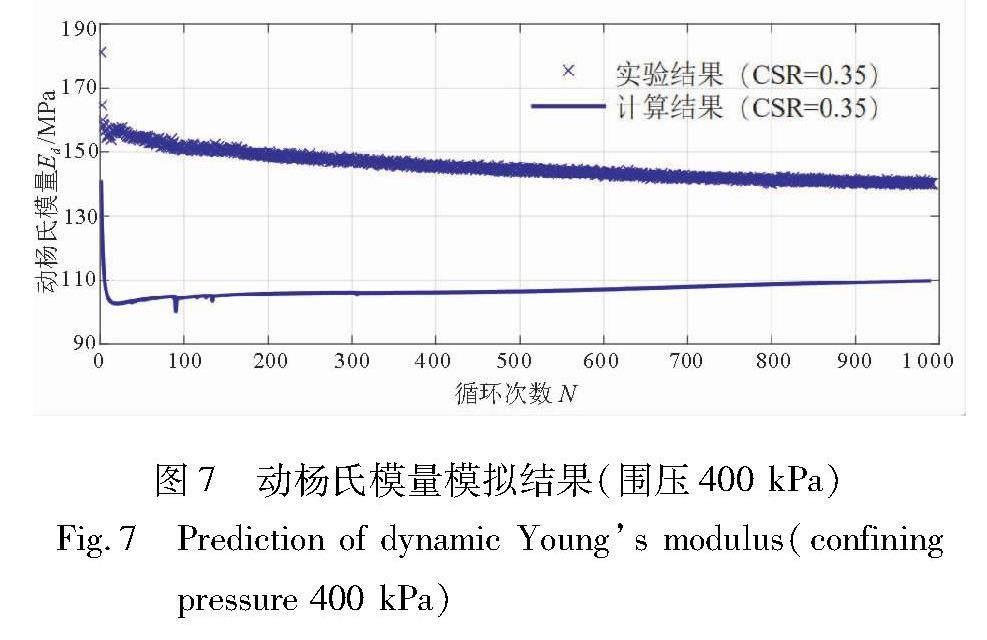
由圖7可知，模型基本預(yù)測(cè)了飽和壓實(shí)黃土動(dòng)楊氏模量衰減規(guī)律。動(dòng)楊氏模量計(jì)算值小于動(dòng)楊氏模量實(shí)驗(yàn)值，但趨勢(shì)一致，且在一個(gè)數(shù)量級(jí)。動(dòng)楊氏模量隨著圍壓的增大而增大，反映了圍壓對(duì)模量的影響。隨著循環(huán)加載次數(shù)的增大，動(dòng)楊氏模量衰減，在102次循環(huán)次數(shù)內(nèi)衰減顯著，反映了循環(huán)加載下黃土結(jié)構(gòu)劣化規(guī)律。

4? 結(jié)語

為預(yù)測(cè)壓實(shí)黃土的動(dòng)本構(gòu)關(guān)系，本文修正了既有邊界面塑性本構(gòu)模型，預(yù)測(cè)分析了飽和壓實(shí)粉質(zhì)黃土動(dòng)三軸試驗(yàn)結(jié)果，得出以下主要結(jié)論。

在邊界面塑性理論框架下，引入了一個(gè)動(dòng)態(tài)映射法則，提出了一個(gè)反映應(yīng)變累積的循環(huán)加載塑性模量表達(dá)式，構(gòu)建了循環(huán)加載下壓實(shí)黃土邊界面塑性本構(gòu)模型，分析了循環(huán)應(yīng)力比對(duì)應(yīng)力應(yīng)變關(guān)系與動(dòng)楊氏模量的影響規(guī)律。

采用該模型預(yù)測(cè)分析了循環(huán)加載下飽和壓實(shí)黃土動(dòng)本構(gòu)關(guān)系，模型計(jì)算結(jié)果與試驗(yàn)結(jié)果分析表明所提出的循環(huán)加載塑性模量能夠反映壓實(shí)黃土的循環(huán)加載非線性、塑性應(yīng)變累積、應(yīng)力應(yīng)變滯回及動(dòng)楊氏模量衰減規(guī)律。研究方法與結(jié)果可為填方壓實(shí)黃土長(zhǎng)期變形分析提供參考。

參考文獻(xiàn)

［1］CORTI R， DIAMBRA A， WOOD D M， et al. Memory surface hardening model for granular soils under repeated loading conditions［J］. Journal of Engineering Mechanics， 2016， 142（12）：04016102.

［2］WANG Z L， DAFALIAS Y F， SHEN C K. Bounding surface hypoplasticity model for sand［J］.Journal of Engineering Mechanics， 1990， 116（5）：983-1001.

［3］方火浪， 沈揚(yáng)， 鄭浩，等. 砂土三維多重機(jī)構(gòu)邊界面模型［J］.巖土工程學(xué)報(bào)， 2017， 39 （7）： 1189-1195.

FANG H L， SHEN Y， ZHENG H， et al. Three-dimensional multi-mechanism bounding surface model for sands［J］.Chinese Journal of Geotechnical Engineering， 2017， 39 （7）： 1189-1195.

［4］董建勛， 劉海笑， 李洲. 適用于砂土循環(huán)加載分析的邊界面塑性模型［J］. 巖土力學(xué)， 2019， 40（2）： 684-692.

DONG J X， LIU H X， LI Z. A bounding surface plasticity model of sand for cyclic loading analysis［J］. Rock and Soil Mechanics， 2019， 40（2）： 684-692.

［5］遲明杰， 趙成剛， 李小軍. 剪脹性砂土邊界面模型的研究［J］. 工程地質(zhì)學(xué)報(bào)， 2008， 16（3）： 128-134.

CHI M J， ZHAO C G， LI X J. A bounding surface plasticity based constitutive model for dilatant sand ［J］. Journal of Engineering Geology， 2008， 16（3）： 128-134.

［6］WOO S I， SALGADO R. Bounding surface modeling of sand with consideration of fabric and its evolution during monotonic shearing［J］. International Journal of Solids and Structures， 2015， 63：277-288.

［7］FANG H L， ZHENG H， ZHENG J. Micromechanics-based multimechanism bounding surface model for sands［J］. International Journal of Plasticity， 2017， 90：242-266.

［8］XIAO Y， LIU H L， LIU H， et al. Unified plastic modulus in the bounding surface plasticity model［J］. Science China Technological Sciences， 2016， 59（6）：932-940.

［9］HU C， LIU H X， HUANG W. Anisotropic bounding-surface plasticity model for the cyclic shakedown and degradation of saturated clay［J］. Computers and Geotechnics， 2012， 44： 34-47.

［10］KIM T， JUNG Y H. A new perspective on bounding surface plasticity： The moving projection origin［J］. KSCE Journal of Civil Engineering， 2017， 21（3）：652-658.

［11］ZHOU C， NG C W W. Simulating the cyclic behaviour of unsaturated soil at various temperatures using a bounding surface model［J］. Géotechnique， 2016， 66（4）：344-350.

［12］RUSSELL A R， KHALILI N. A unified bounding surface plasticity model for unsaturated soils［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2006， 30（3）：181-212.

［13］YANG C， CUI Y J， PEREIRA J M， et al. A constitutive model for unsaturated cemented soils under cyclic loading［J］. Computers and Geotechnics， 2008， 35（6）：853-859.

［14］FU Y K， GAO Z W， HONG Y， et al. Destructuration of saturated natural loess： From experiments to constitutive modeling［J］. International Journal of Damage Mechanics， 2021， 30（4）：575-594.

［15］褚峰， 張宏剛， 邵生俊. 隴東Q3結(jié)構(gòu)性黃土壓剪損傷本構(gòu)模型試驗(yàn)研究［J］.巖土力學(xué)， 2019， 40（10）： 3855-3870.

CHU F， ZHANG H G， SHAO S J. Experimental study of constitutive model of Longdong Q3 structural loess with compressive and shearing damage ［J］. Rock and Soil Mechanics， 2019， 40（10）： 3855-3870.

［16］侯樂樂， 翁效林， 崔藝鋮， 等.? K0固結(jié)結(jié)構(gòu)性黃土的各向異性本構(gòu)模型［J］.巖石力學(xué)與工程學(xué)報(bào)， 2022， 41（10）： 2124-2134.

HOU L L， WENG X L， CUI Y C， et al. Critical state constitutive model of K0 consolidated structural loess［J］.Chinese Journal of Rock Mechanics and Engineering， 2022， 41（10）： 2124-2134.

［17］姚志華， 陳正漢， 方祥位， 等. 非飽和原狀黃土彈塑性損傷流固耦合模型及其初步應(yīng)用［J］.巖土力學(xué)， 2019， 40（1）： 216-226.

YAO Z H， CHEN Z H， FANG X W， et al. Elastoplastic damage seepage-consolidation coupled model of unsaturated intact loess and its application ［J］. Rock and Soil Mechanics， 2019， 40（1）： 216-226.

［18］蔣明鏡. 現(xiàn)代土力學(xué)研究的新視野： 宏微觀土力學(xué)［J］.巖土工程學(xué)報(bào)， 2019， 41（2）： 195-254.

JIANG M J. New paradigm for modern soil mechanics：Geomechanics from micro to macro ［J］. Chinese Journal of Geotechnical Engineering， 2019， 41（2）： 195-254.

［19］康孝森， 廖紅建， 黃強(qiáng)兵， 等. 結(jié)構(gòu)性黃土的臨界壓力比及其邊界面塑性本構(gòu)模型預(yù)測(cè)［J］.巖土力學(xué)， 2022， 43（6）： 1469-1480.

KANG X S， LIAO H J， HUANG Q B， et al. Spacing ratio of structural loess and its prediction using bounding surface plasticity model ［J］. Rock and Soil Mechanics， 2022， 43（6）： 1469-1480.

［20］崔廣芹. 飽和黃土動(dòng)力本構(gòu)模型及地鐵隧道周圍土層變形分析［D］. 西安：西安建筑科技大學(xué)， 2014.

［21］JUNG Y H， LEE J H. Experimental validation of the radial mapping rule in bounding surface plasticity model［J］. Journal of the Korean Geotechnical Society， 2013， 29（1）： 171-181.

［22］KAN M E， TAIEBAT H A， KHALILI N. Simplified mapping rule for bounding surface simulation of complex loading paths in granular materials［J］. International Journal of Geomechanics， 2014， 14（2）：239-253.

［23］XU L， COOP M R. The mechanics of a saturated silty loess with a transitional mode［J］. Géotechnique， 2017， 67（7）： 581-596.

［24］KANG X S， LIAO H J， HUANG Q B， et al. Enhanced anisotropic bounding surface plasticity model considering modified spacing ratio of anisotropically consolidated clay［J］. Acta Geotechnica， 2022， 17（6）： 2213-2233.

［25］DAFALIAS Y F， TAIEBAT M. Anatomy of rotational hardening in clay plasticity［J］. Géotechnique， 2013， 63（16）： 1406-1418.

［26］SEIDALINOV G， TAIEBAT M. Bounding surface SANICLAY plasticity model for cyclic clay behavior［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2014， 38（7）：702-724.

［27］代倩， 廖紅建， 康孝森， 等. 動(dòng)荷載下填方體壓實(shí)黃土動(dòng)應(yīng)變與動(dòng)孔壓變化規(guī)律研究［J］.巖土工程學(xué)報(bào)， 2021， 43（S1）： 235-240.

DAI Q， LIAO H J， KANG X S， et al. Behaviors of dynamic strain and pore pressure of compacted loess in loess-filled foundation induced by dynamic loading［J］. Chinese Journal of Geotechnical Engineering， 2021， 43（S1）： 235-240.

（編? 輯? 張? 歡）