動車組頭車聲固耦合模態分析及多目標優化

于 洋, 曹啟軍, 劉春艷, 陳秉智, 于春洋

(1. 中車長春軌道客車股份有限公司,長春 130021; 2.大連交通大學 機車車輛工程學院,遼寧 大連 116028)

高速動車組車體結構的固有振動特性是結構設計中考慮動態載荷影響的重要參數。模態分析旨在提取結構固有頻率和振型,為動力學分析和動態設計奠定基礎。通過對車體結構進行模態分析,可評定其動態特性能否滿足設計要求,確保列車具有良好的乘車舒適性,并為后續動力學優化設計提供依據。

為全面分析車體結構的動態特性,除了分析結構的固有振動特性,還需要進一步考慮聲場對結構的反饋作用,即聲固耦合因素的影響。目前,高速列車本征動力學特性研究主要集中在結構固有頻率及模態振型分析[1-5],關于聲場模態測試及聲-結構耦合模態分析研究有待于深入開展。文獻[6-8]中的高速列車聲學模態分析僅涉及內聲場,未考慮結構與聲場的耦合效應。楊志康[9]以中間車為研究對象,分析了考慮耦合作用下的結構動態特性和車內聲壓變化。徐凱等[10]建立CRH 5型動車組車廂聲固耦合有限元模型,綜合比較結構模態、聲場模態和聲固耦合模態的振型特點,發現引入耦合因素影響的系統振型與非耦合結構模態相對應,聲場對耦合系統模態影響較小。劉太祥等[11-12]也建立了動車組聲固耦合有限元模型,分析耦合狀態下的車體結構固有振型及內聲場聲壓分布特征。上述研究僅考慮結構與內部聲場的耦合,未綜合考慮外部聲學介質對系統動力學特性的影響;此外,相關工作僅停留在耦合因素對系統聲振特性影響的描述性分析階段,并未針對避免該耦合共振現象進行優化設計。

輕量化設計是高速列車結構優化理論的重要組成部分。近年來,在保證車體結構固有振動指標可靠的前提下進行輕量化研究受到廣泛關注[13-14]。現有研究僅將車體結構的一階垂彎頻率納入優化模型的約束條件,并未充分考慮聲固耦合共振對車體結構振動響應的影響。對于聲振耦合系統共振影響因素的理論研究已有不少成果,如Pan[15]基于模態耦合分析法研究了簡支板和矩形聲腔構成耦合系統的模態特性,分析了簡支板厚度、阻尼等因素對耦合系統特性的影響。王園等[16]在文獻[15]的基礎上,進一步分析了聲腔深度變化對板-聲腔系統耦合動力學特性的影響,其研究對象仍為簡支板與矩形聲腔組成的簡單系統,未涉及復雜結構與聲腔之間的耦合問題。以能量為基本變量的統計能量分析方法是研究復雜系統結構和聲場的相互作用的有效方法,也是中高頻聲振動力學分析的主流手段。該方法將研究對象劃分為若干個子系統,建立穩態振動狀態下各子系統之間的能量流平衡方程[17]。Louisell[18]在研究線性耦合振蕩器運動方程時引入傳遞因子概念以衡量不同振子模態間能量傳遞程度,發現當兩個非耦合振子模態頻率相同時能量完全傳遞。Lyon[19]假定弱線性耦合,計算了隨機載荷激勵下兩個諧波振蕩器之間的功率流,發現功率流與兩個振蕩器平均模態能量差成正比,當耦合系數中聲場與結構固有頻率相等時模態間能量傳遞效率最高。針對以上研究可見,為減弱高速列車耦合共振作用,降低模態之間的能量傳遞,需要避免車體結構及聲場有接近的模態頻率。

當聲腔與結構子系統的固有頻率接近時,會產生聲固耦合共振現象,造成結構子系統振動幅度增大、聲腔內聲壓升高,從而加劇結構的疲勞破壞和失效風險,產生噪聲污染和聽力損害。朱凱等[20]以某拖拉機駕駛室為研究對象建立聲固耦合模型并進行模態分析,發現駕駛室內聲壓作用引起結構振動頻率發生一定變化;龔京風等[21]利用聲固耦合數值模型分析不同部位的耦合效應對充水膨脹腔消聲器聲學性能的影響,發現周向腔壁的耦合效應導致傳遞損失曲線向低頻偏移,膨脹腔壁的耦合作用引起傳遞損失曲線出現明顯峰值;艾延廷等[22]分析燃燒室封閉結構的聲振耦合特性,發現聲場的反饋作用相當于增加了結構的附加質量,使結構固有頻率下降,并且得出了耦合頻率的具體數值;張義波[23]在商用車駕駛室的結構噪聲分析研究中發現,在兩種特定工況下166 Hz附近車身結構與聲腔發生耦合共振,作者通過形貌優化提高結構固有頻率以增加結構和聲腔的固有頻率間隔,消除了共振影響,降低最大峰值聲壓。由此可知,調節聲場及結構固有頻率以避免聲固耦合共振現象具有較高理論價值及工程意義。

本文從有限元法、統計能量法兩方面闡述高速列車聲固耦合共振影響因素的理論基礎;基于模態等效和質量等效原則對高速列車頭車結構進行有限元建模,分別提取結構模態、聲場模態及考慮內外聲場作用的聲固耦合模態;基于結構模態提取結果進行減重優化,實現滿足車體動態特性要求的最佳質量分布;為消除耦合共振影響、提高車廂舒適度,在車體減重設計模型基礎上引入聲-結構耦合共振關鍵參數,建立舒適性與輕量化同步提升的多目標優化體系。

1 聲固耦合共振理論

1.1 有限元理論中的共振影響因素

有限元模態分析將動力學方程組中的物理坐標轉換成模態坐標以實現方程組的解耦,從而得到系統的模態參數。針對高速列車頭車聲固耦合系統,建立有限元模型并將其離散成有限個自由度,當結構表面和內部聲場受到簡諧激勵時,該耦合系統離散形式的結構和聲場動力學方程分別為[24]

(Ks+jωDs-ω2Ms)U=Fs+Fa

(1)

(Ka+jωDa-ω2Ma)P=-ω2RU

(2)

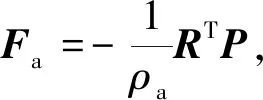
式(1),式(2)可通過模態法求解,利用模態分析計算出式(1),式(2)的互異特征值和相應的特征向量,從而將式(1),式(2)中的位移和聲壓響應向量由物理坐標系轉換為模態坐標系[25]

U=Ψη
P=Φξ

(3)

式中:Ψ和Φ分別為解耦的彈性邊界結構模態矩陣和剛性壁聲場模態矩陣;η和ξ分別為對應的結構和聲場模態坐標向量。

式(1)中,與結構激勵Fs的作用相比,聲壓變化對結構邊界運動的影響非常小,因此可將聲壓載荷Fa忽略。假定結構系統與聲場系統的阻尼均為比例阻尼,將式(3)代入式(1),式(2)中,并且分別左乘結構和聲場的模態轉置矩陣ΨT、ΦT,可得模態坐標系下的動力學方程

(4)

式中:I為單位矩陣;c為結構模態與聲場模態之間的耦合矩陣,矩陣內的元素為

(6)

η可由式(4)直接表示,將其代入式(5)中,推導出聲壓P的表達式為

(7)

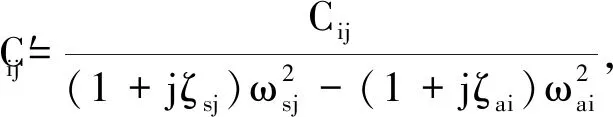
在阻尼很小的情況下,忽略結構與聲場的阻尼因子ζsj與ζai,聲壓P近似為

(8)

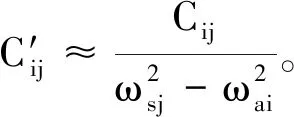
1.2 統計能量分析中的共振影響因素

有限元法將系統離散成有限個單元,建立由單元節點構成的動力學微分方程。該方法主要適用于中低頻域的系統動力學問題,在結構動力學特性分析時只能考慮有限數量的低階模態,并且隨著頻域和結構復雜度的增加,分析誤差和難度相應增大,導致難以確定復雜系統的高階模態參數[26]。相比之下,統計能量方法將系統劃分為N個共振子系統,并假設各子系統之間相互獨立且能夠存儲振動能量。該方法通過計算子系統之間的功率流和功率流平衡方程以獲得各子系統能量儲存和傳遞情況,從而反映子系統振動狀態,適合解決高頻區內復雜系統動力學問題[27]。

統計能量分析基本方程為功率流平衡方程,穩態振動時,在子系統激勵相互獨立及保守弱耦合(耦合損耗因子明顯小于內損耗因子)情況下,各子系統線性功率流平衡方程可表示為

(9)

式中:Πi,in為外界對子系統i的輸入功率;Πi,diss為子系統i的阻尼損耗功率;Πij為子系統i傳遞到子系統j的功率(雙向),可寫為[28]

Πij=βij(Ei-Ej)

(10)

式中:

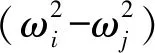
本節從有限元理論、統計能量理論兩個角度分析耦合共振影響因素,發現在中低頻域和高頻區間內的系統動力學問題中,當非耦合結構和聲場系統模態頻率接近時會導致系統間能量傳遞顯著,表現為聲腔內部聲壓急劇升高、結構表面劇烈振動。因此,為減弱或避免動車組頭車結構與聲場發生耦合共振、提高車廂舒適性,需要避免結構與聲場模態頻率接近。

2 非耦合狀態下頭車模態分析

2.1 模態等效以及質量等效原則

動車組頭車地板、側墻、頂板、端墻等部位均為鋁合金中空型材結構,由內外蒙皮和中間的加強筋構成。若以傳統實體單元進行有限元建模,需要在狹小筋板處設置較高精度的網格,并且需要大量三維單元劃分中空型材封閉的聲場空間,這將限制模態提取速度和結構優化效率,同時對計算機硬件條件要求過高。為克服上述問題,基于模態等效原則[29],采用文獻[30]中等效建模方法,保持中空型材的內外蒙皮參數不變,將中間的加強筋及空氣等效為虛擬材料,形成等效NVH三層板,使等效板與原型材結構動態特性誤差控制在10%以內,等效前后結構整體的幾何尺寸、密度相同。中空型材的模態等效示意圖如圖1所示。

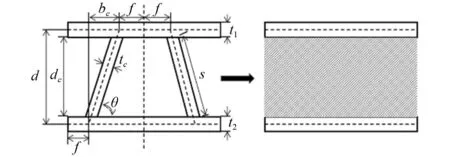
圖1 中空型材模態等效示意圖Fig.1 Schematic diagram of the hollow profile based on the modal equivalence

基于等質量原則應用中空型材結構的等效密度方法修正等效板的材料密度參數[31],假定鋁合金型材的密度為ρ,該型材結構中間層的等效密度ρe為

(11)

根據以上兩種等效方法,可將頭車中空型材結構等效為NVH三層板,具體的材料屬性參數如表1所示。

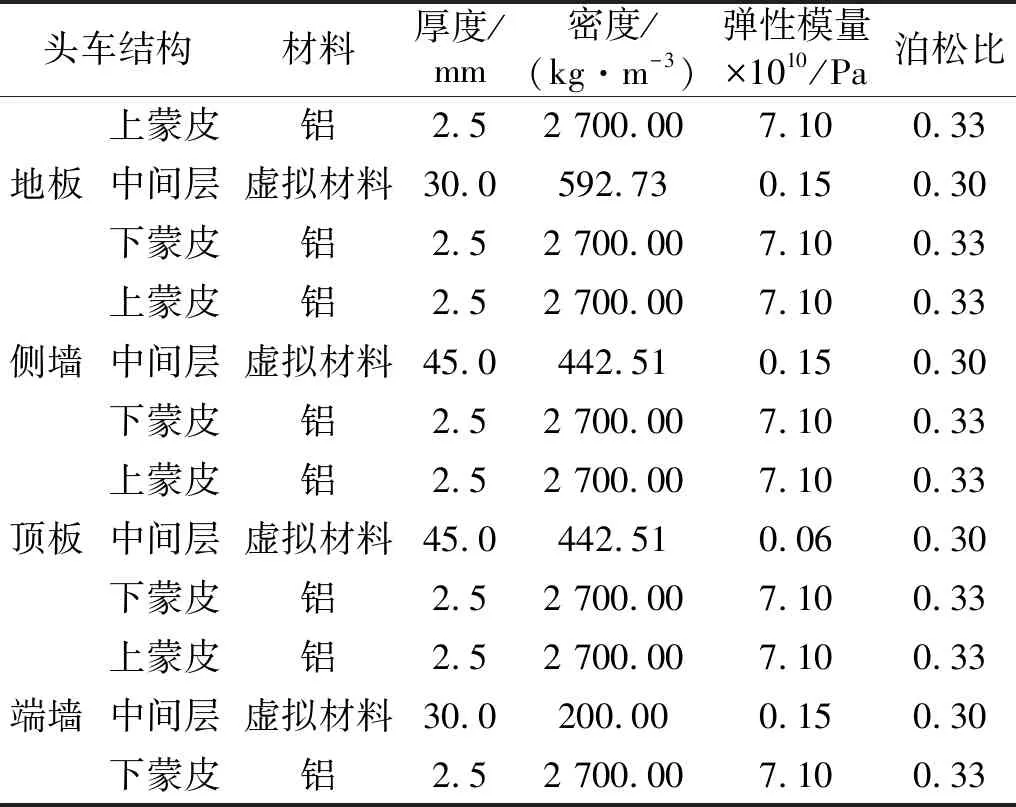
表1 等效結構材料屬性Tab.1 Properties of equivalent structural materials

通過有限元軟件COMSOL對幾何模型進行網格劃分,車身結構和車內聲場分別采用殼單元及四面體域網格離散。考慮到20 Hz是人耳能感受到的最低頻率,且低頻噪聲主要源于200 Hz以下的車身結構振動,因此模態分析的頻率區間選取20～200 Hz。依據相關網格尺寸標準,聲腔網格最大單元的邊長不超過最高計算頻率200 Hz處波長的1/6。整車共劃分30 752個三角形殼結構單元,251 657個四面體聲腔單元,且車體各部分的板厚按照實際參數定義為實常數,車體有限元離散模型如圖2所示。

圖2 車體有限元模型Fig.2 EMU finite element model

2.2 結構模態分析結果

結構模態分析采用無約束自由邊界條件,前6階模態主要為車身相對于轉向架的低頻剛體振動位移,即剛體模態,不予考慮。表2為忽略剛體模態的前6階及第12階模態固有頻率及振型描述,發現不同階次結構模態的相對變形位置不同,且隨著階數增加,模態振型更加復雜。車體1階垂向彎曲模態出現在第5階,其固有頻率為19.314 Hz。根據文獻[32],整備車體的彎曲振動頻率總體降低約20%,因此該動車組頭車整備狀態下的彎曲振動頻率約為15.45 Hz,滿足《200 km/h 及以上速度級鐵道車輛強度設計及試驗鑒定暫行規定》標準[33]中的要求:“車體整備狀態下最低彎曲振動頻率大于10 Hz”。

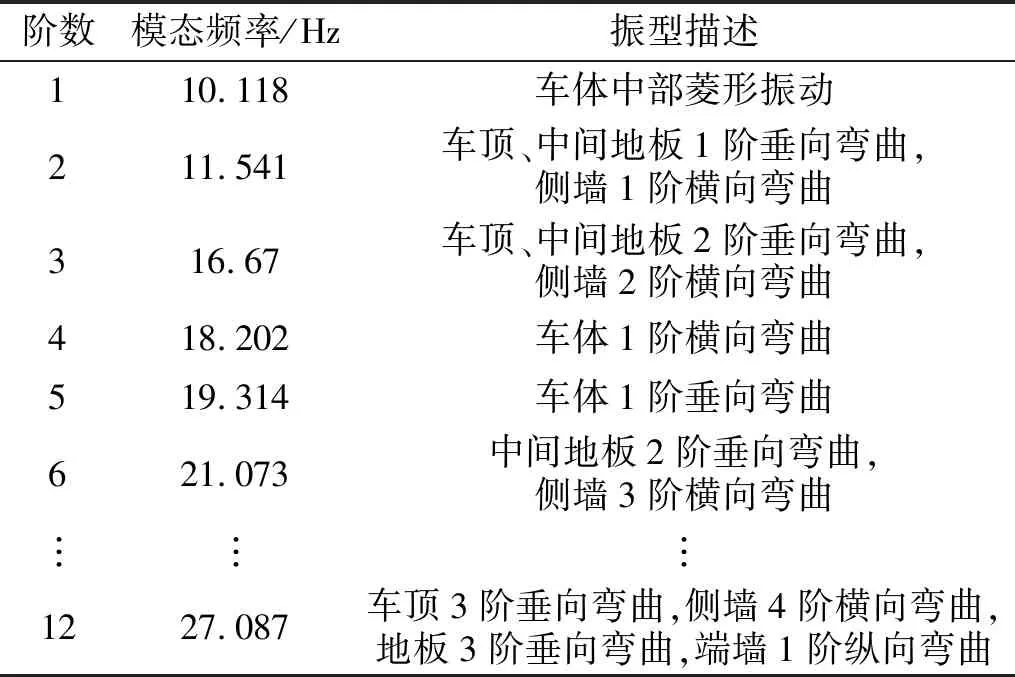
表2 頭車結構模態Tab.2 Structural modes of head car

2.3 聲場模態分析結果

聲場模態頻率是聲腔內部聲音的共鳴頻率,在各階模態頻率附近,車室內的空腔會產生聲學共振,導致聲壓急劇升高。對頭車室內空腔聲學模態進行分析可確定是否存在共振現象,為車內聲學結構設計提供依據。計算前20階室內空腔聲學模態,其中第1階模態頻率為0,表示車室內各點聲壓變化的幅值相同,類似于結構模態中的剛體模態,忽略不計。表3為忽略一致聲壓的前6階聲場模態固有頻率及振型描述,發現低階均為縱向聲學模態,聲壓沿縱向分布,模態振型隨著頻率的增加而復雜;表中的第四階聲場模態頻率(27.335 Hz)與第12階結構模態頻率(27.087 Hz)十分接近,根據耦合共振影響因素理論,在該頻率附近車內聲腔與車身結構發生耦合共振的概率顯著提高,從而加劇室內噪聲,影響旅客乘車舒適性[34]。因此,針對該耦合共振問題,有必要進行相關的優化設計使結構和聲場模態頻率錯開。

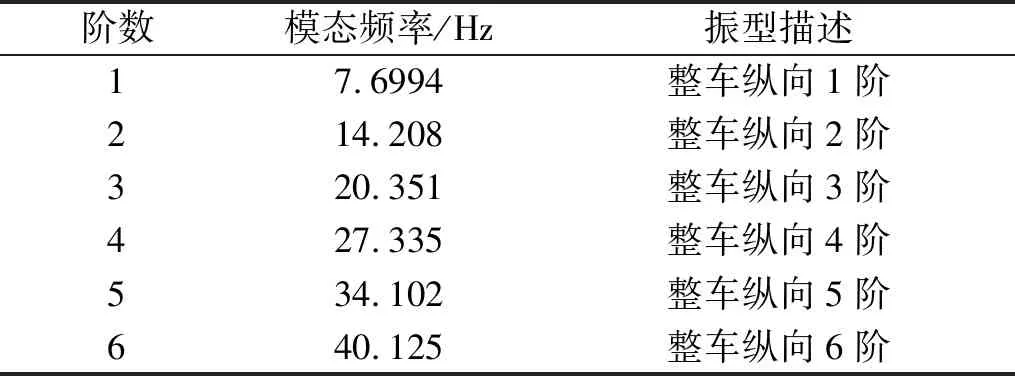
表3 頭車聲場模態Tab.3 Acoustic modes of head car

3 考慮內、外聲場影響的頭車聲固耦合模態分析

為確保運行時高速列車的結構穩定性和乘坐舒適度,需要分析聲場耦合作用下頭車結構的固有振動特性。傳統的聲固耦合分析方法僅考慮內聲場影響,忽略了外聲場作用。然而,高速列車在運行過程中會受到復雜的氣動載荷,導致頭車表面結構產生振動和聲輻射。這些聲輻射不僅造成沿線噪聲污染,還會通過結構傳遞和空氣透過等方式進入車廂內部空間,影響車身結構的振動幅度及乘客的聽覺感受。因此,在頭車設計過程中,需要綜合考慮內聲場、外聲場和頭車結構之間的模態耦合效應,以評估頭車結構動力學特性,為其幾何形狀和參數優化提供依據。

對于兩側均帶有聲學介質的殼結構,由于厚度較小,結構上下表面之間的壓力分布有所不同,可通過在壓力變量上引入切口實現該壓力的不連續性,相當于在結構中間添加界面使其上下表面分離,并確保上下表面能夠連接起來。該結構-內、外聲場耦合邊界條件為

(12)

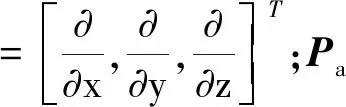
為模擬聲波在外聲場傳播的無限性,構建頭車結構有限元模型的外聲場時,需要沿模型外部人為地截斷邊界,要求該邊界能夠吸收所有出射波且消除聲波在邊界的反射。目前,諸多學者提出多種吸收邊界條件,但是受邊界吸收角度的限制,未能達到理想的吸收效果[35]。完美匹配層(perfect matched layer,PML)是Berenger[36]針對電磁波傳播情況提出的一種吸收邊界條件,應用PML研究聲固耦合系統的聲輻射問題時,PML區域內聲學波動方程中聲壓的坐標向量由實坐標轉換為復數坐標,在該坐標中引入吸收函數使聲波在進入PML層后逐漸衰減,最終實現出射聲波的完美吸收。PML域內的聲波方程表示為[37]

(13)

(15)

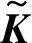
(16)

忽略外載荷及阻尼影響,式(15)演變為PML域內的聲學特征值方程,表示為

(17)

PML不受邊界吸收角度的限制,可以完全吸收任意方向和頻率的波而不產生邊界反射,因此選取完美匹配層吸收邊界構建外聲場有限元模型。基于軟件COMSOL在結構-內聲場耦合有限元模型外構建球形完美匹配層。建模時球體半徑設置為目標模型半徑的2至4倍。PML層網格大小至少為最小波長λmin的八分之一,結構-內、外聲場耦合有限元模型如圖3所示,其中內聲場包含216 958個四面體網格,外聲場包含10 520 860個四面體網格,PML層由677 552個棱柱網格構成。

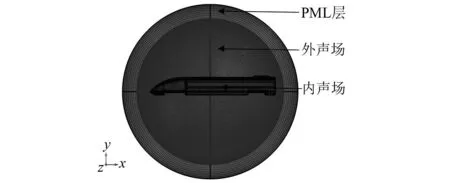
圖3 結構-聲場耦合有限元模型Fig.3 Structure-acoustic coupling finite element model

表4為結構-內、外聲場耦合系統模態,圖4為相應的模態振型云圖。對比表4與表2,發現由于內、外聲場的作用,車身結構模態固有頻率整體下降,且前6階均為新增加的模態振型。對比表4與表3,發現耦合聲場第4階與非耦合聲場第1階模態振型相同,固有頻率略有降低;由于內、外聲場的耦合作用使車內聲壓發生變化,產生新的內聲場模態振型,內部聲壓除了沿縱向變化外,還沿著橫向和垂向變化;隨著階數增加,聲場振型逐漸向高階演變。表4與表2、表3綜合對比,發現前6階耦合模態頻率值與非耦合結構模態頻率值相近,而與非耦合聲場模態頻率值差距明顯,表明耦合系統模態主要受車身結構影響,內、外聲場對耦合模態的貢獻較小。

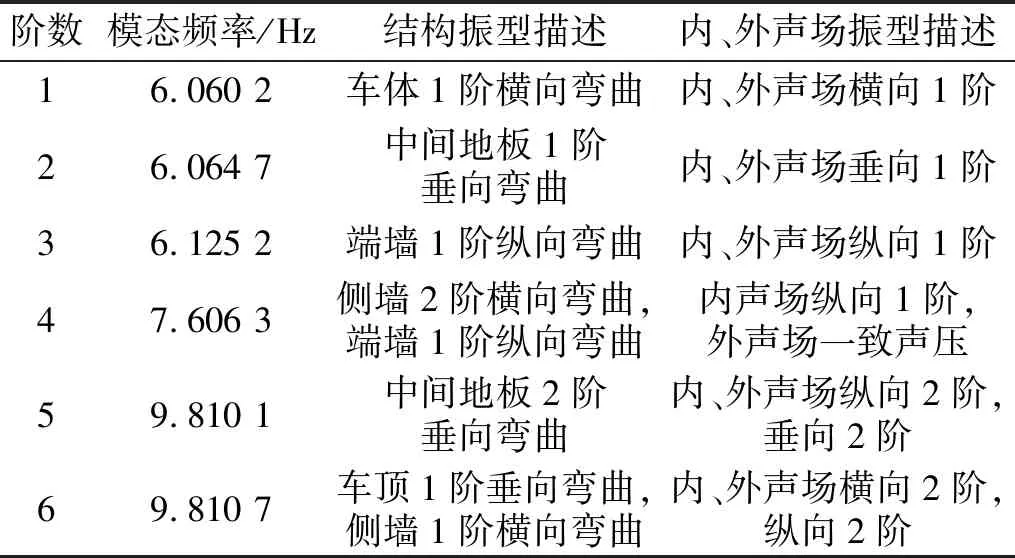
表4 結構-聲場耦合模態Tab.4 Structure-acoustic coupling modes

圖4 結構-聲場耦合模態振型Fig.4 Structure-acoustic coupling mode shapes

對比該耦合系統中的內聲場模態與外聲場模態振型,發現兩者振型基本一致(除了第4階外聲場模態振型為一致聲壓)。振型耦合系數反映了結構與聲場子系統的模態振型耦合強弱,該系數與耦合面上結構和聲場的模態振型有關。該系數絕對值越大,子系統間的耦合越強,反之則表示子系統間的耦合較弱。對于具有復雜幾何構型的工程裝備(如本文的頭車聲固耦合系統),模態振型耦合系數可以通過有限元方法獲取。

忽略式(6)中結構與聲場形函數矩陣及聲腔密度參數,形成積分形式的振型耦合系數Oij

(18)

利用有限元法獲取耦合面上外聲場和結構子系統模態振型在各個節點上的分量,將聲腔和結構的模態振型函數轉換為節點編號為自變量的函數,代入式(18)后可寫為[38]

(19)

式中:q為耦合面上的節點編號;qall為耦合面上的總節點數。

表5顯示了該頭車聲固耦合系統的振型耦合系數有限元結果。從表中可以看出,在該耦合系統中,振型耦合系數的絕對值較小,均小于0.1。這表明該耦合系統的結構和聲腔子系統較為復雜,導致其模態振型分布不規則,使得耦合面上的結構和聲腔振型的相似度降低,因而振型耦合系數普遍較低。另一方面,這也反映了該耦合系統的結構與聲場振型之間的耦合強度較弱。

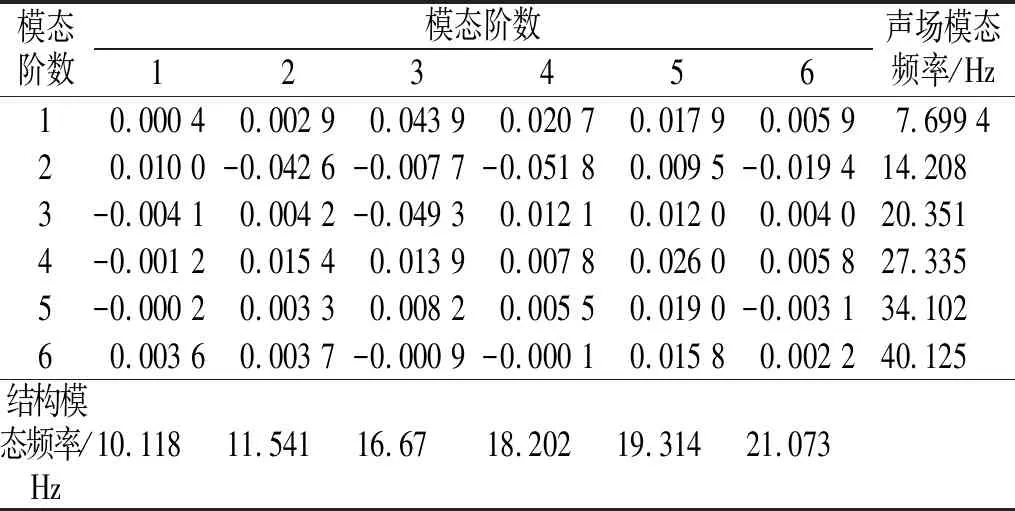
表5 振型耦合系數有限元計算結果Tab.5 FEM result of the mode shape coupling coefficient

4 頭車減重優化設計

4.1 優化問題

本優化設計旨在保證車體結構本征動力學特性不降低的情況下,實現動車組頭車結構質量最小化。

(1)設計變量

將車體結構板厚作為設計變量。由于將實體型材結構等效為NVH三層板結構,分配設計變量時先將頭車結構劃分為3個主要部分,即地板、側墻、車頂(端墻部位對于車體質量變化影響程度較小,不作為設計變量),每部分進一步分為外蒙皮、中間層、內蒙皮等3個變量。由此確定9個部分的板厚作為優化設計的變量,即X=[x11,x12,x13,…,x31,x32,x33]T。

(2)約束條件

①頻率約束:結構一階垂向彎曲振動頻率f不低于初始值。

②邊界約束:又稱為區間約束,規定了設計變量的取值范圍。對于高速動車組車體結構,其板厚可以根據經驗和工藝條件等因素確定變化的上下限,具體值見4.3節中表6。

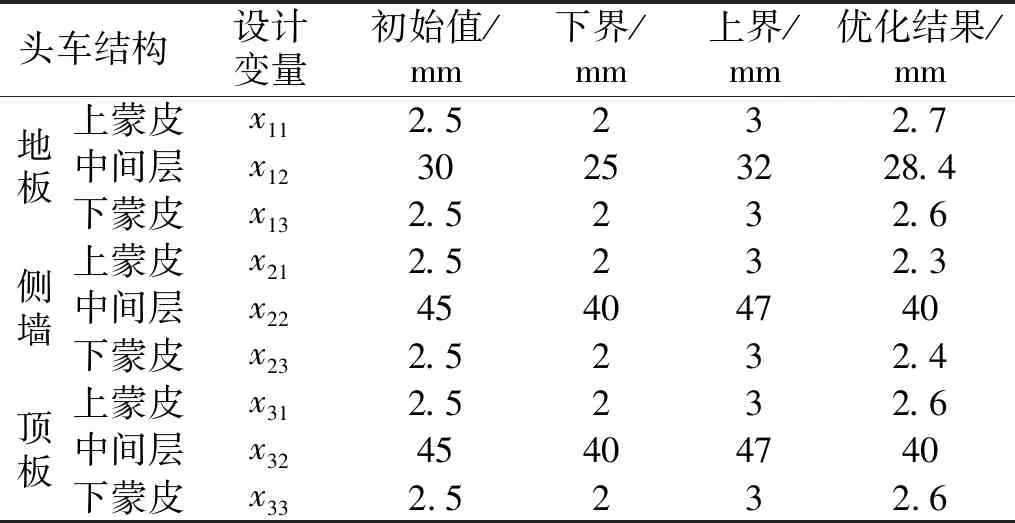
表6 減重優化結果Tab.6 Weight reduction optimization results

(3)優化模型

根據以上對高速動車組車體減重優化的參數選取及描述,該優化設計的數學模型表示為

(20)

4.2 優化算法

本次優化設計基于有限元分析軟件COMSOL優化平臺,該平臺提供了梯度算法和無梯度算法兩類優化算法。梯度算法適用于目標函數可微或連續的情況,優化速度較快,但容易陷入局部最優。無梯度算法不依賴目標函數導數信息,只需要對目標函數進行采樣,根據采樣結果確定下一步的搜索方向。該算法適用于目標函數不可微或不連續的情況,優化穩定性較好,計算時間較長。考慮到優化的穩定性,本文選取無梯度優化算法中的Nelder-Mead算法。該算法通過在控制變量空間中構造由N+1個點組成的單純形,其中N為控制變量的數量,對單純形中的最差點進行反射、展開和收縮以改進單純形的形狀和位置,從而逼近目標函數的最優值。

Nelder-Mead算法使用優化容差(默認值為0.01)作為終止條件,該參數可用于判斷優化是否收斂,反映了優化進程中目標函數值的變化幅度。迭代過程中,在優化步長大于或等于優化容差的比例控制變量中,無法找到改善當前目標函數值的方向時,該算法就會停止迭代,輸出最優解。

4.3 優化結果

根據Nelder-Mead算法經過約1 000次迭代計算,獲得了可行域內的優化解,優化過程中目標函數的迭代歷史如圖5所示,由于該算法每次迭代僅沿著單純形的邊移動到相鄰頂點,而非直接向最優解方向前進,因此存在多余的轉彎和折返,在該圖中表現為前100次迭代優化幅度及振蕩性較大,后期緩慢下降。優化后的設計變量值如表6所示。

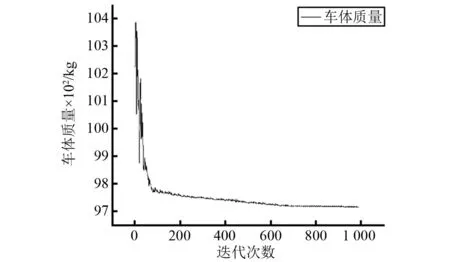
圖5 減重優化迭代歷史Fig.5 Iterations of weight reduction optimization

從表6可以看出,由于目標函數設置為車體質量最小化,大多數部位的板厚有所下降,優化后側墻和頂板的中間層厚度甚至達到下限,而地板上下蒙皮及中間層、頂板上下蒙皮的對應厚度在優化后略有增加。這是因為在減重進程中受到一階垂彎模態頻率約束的限制,為保證車體本征動態特性不劣于初始值,需要適當提升部分位置的厚度,導致部分設計變量未能達到限值。優化后車體結構質量由10 225 kg降低到9 715 kg,相對減重率為5%,同時結構一階垂彎模態頻率也控制在初始值以上,為19.314 Hz,滿足設計要求。因此,優化結果有效且可行。

5 耦合共振多目標優化設計

5.1 優化問題

本節在車體減重設計模型的基礎上,進一步考慮結構與聲場的耦合共振問題。對比非耦合結構和聲場模態分析結果,發現結構第12階模態頻率(27.087 Hz)與聲場第4階模態頻率(27.335 Hz)最接近,產生耦合共振作用的概率較高,易導致聲腔內部聲壓升高、結構振動劇烈,降低旅客乘坐舒適度。因此,為消除耦合共振影響,將該結構與聲場模態接近的固有頻率差最大化作為另一個優化目標,形成頭車輕量化與舒適性指標同步提升的多目標優化體系。優化設計的變量與減重優化相同,不再重復說明。

(1)約束條件

①頻率約束:結構一階垂向彎曲振動自振頻率f不低于初始值。

②邊界約束:設計變量取值范圍與上節一致。

(2)優化數學模型

根據以上對高速動車組車體多目標優化的參數選取和描述,其優化數學模型可以表示為

(21)

5.2 優化結果

經過209次迭代,獲得了可行域內的優化解,優化過程的目標函數迭代歷史如圖6所示,優化前期目標函數波動較大,曲線振蕩,后期逐漸趨于穩定。優化后的設計變量值如表7所示。

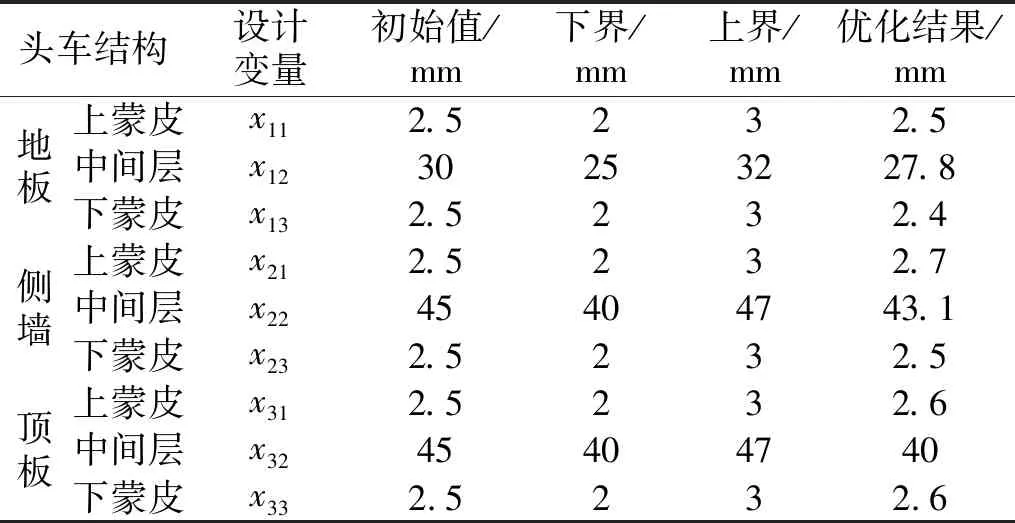
表7 多目標優化結果Tab.7 Multi-objective optimization results

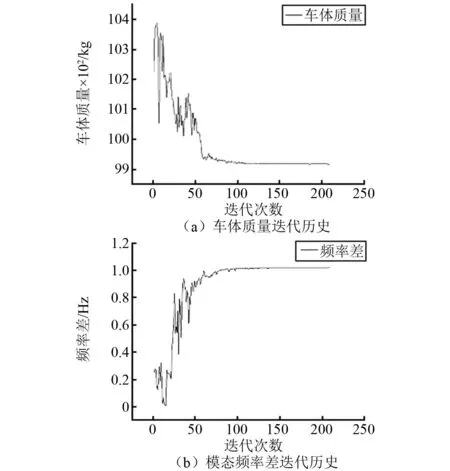
圖6 多目標優化迭代歷史Fig.6 Iterations of multi-objective optimization

由表7可以看出,地板中間層、側墻上蒙皮及中間層、頂板上下蒙皮的厚度優化后略有增加,地板上蒙皮、側墻下蒙皮厚度保持不變,頂板中間層厚度優化后達到下限。相較于減重優化,本模型引入頻率差作為另一個優化目標,導致優化后達到下限的設計變量進一步減少。車體結構質量由10 225 kg降到9 916.4 kg,相對減重率為3%。此外,結構模態頻率由27.087 Hz下降至26.315 Hz,聲場模態頻率保持不變,為27.335 Hz,兩者模態頻率差由0.25 Hz提高到1.02 Hz。結構一階垂彎模態頻率控制在約束值以內,為19.314 Hz。

6 結 論

本文基于模態等效和質量等效原則建立動車組頭車有限元模型,分析了結構和聲場模態的振型特征,進一步考慮內、外聲場對結構的反饋作用進行結構-內、外聲場耦合模態分析。基于模態分析結果,在保證車體結構的動力學特性前提下,構建了動車組頭車結構的減重優化模型。最后在該減重優化模型的基礎上進一步提取結構和聲場固有頻率值接近的非耦合模態階次,將二者的頻率差最大化也作為優化目標以避免耦合共振的影響,形成頭車輕量化與舒適性指標同步提升的多目標優化體系。主要研究結論如下:

(1)車體一階垂向彎曲頻率符合軌道車輛設計規范。聲場與結構模態存在相近頻率值,增加車內聲場與車身結構耦合共振概率,影響列車運行安全性和旅客乘車舒適性。內、外聲場的耦合作用導致結構模態固有頻率略有降低,產生新的固有頻率和聲場模態振型,論證了模態分析中考慮聲固耦合因素的必要性。耦合系統模態主要受頭車結構影響,聲場對其貢獻較小。

(2)減重優化效果為:車體結構質量降低510 kg,相對減重5%,且保持結構動力學特性優于初始狀態。多目標優化后,車體結構質量減重3%,同時結構與聲場模態頻率差由0.25 Hz提高到1.02 Hz,有效避免聲固耦合共振影響。