NTRU 格上高效緊湊密鑰封裝方案

梁志闖 鄭婕妤 趙運磊,2

1（復旦大學計算機科學技術學院 上海 200433）

2（密碼科學技術國家重點實驗室 北京 100036）

（zcliang21@m.fudan.edu.cn）

密碼學是現代網絡安全的基石.現階段廣泛使用的公鑰密碼體制，如公鑰加密、密鑰封裝、數字簽名等，多數是基于經典的困難問題構造的，如求解大整數分解、（橢圓）離散對數等困難問題.這些密碼方案在當今互聯網協議，如SSL/TLS，?PSec 等中扮演了無可替代的角色，如保證通信內容的機密性、通信雙方的身份認證、消息的完整性等.盡管針對這些數論問題目前最好的經典求解算法的時間復雜度是指數或亞指數級別，至少是超多項式級別的，但近些年來隨著量子計算的飛速發展，已有相關研究表明存在多項式時間的量子算法可以完全求解它們.例如，美國科學家Shor[1]提出可在量子計算機中以多項式時間求解大整數分解和（橢圓）離散對數問題的量子算法.量子計算相關技術的發展日新月異.考慮到量子計算技術對現有公鑰密碼的顛覆性威脅，目前很多國家、公司和學術界已提前研究和布局能夠抵抗量子攻擊的密碼學—后量子密碼學（post-quantum cryptography，PQC）.

事實上，早在2016 年，美國國家標準技術研究所（National ?nstitute of Standards and Technology，N?ST）已經正式開啟了對公鑰加密（public key encryption，PKE）方案、密鑰封裝方案（key encapsulation mechanism，KEM）和數字簽名這3 種密鑰原語的后量子密碼方案標準征集活動，且目前已經評選出第3輪結果并選定擬標準化的方案[2].我國也在2019 年舉行后量子密碼算法競賽，并于2020 年評選出獲獎方案[3].

目前，后量子密碼學的類型主要分為：基于哈希的、基于多變量的、基于同源的、基于編碼的以及基于格的.其中基于格構造的后量子密碼方案不僅具有平均情形到最糟情形的困難性規約，還在安全性、通信帶寬和計算效率等方面表現均衡.在美國N?ST和我國舉辦的后量子密碼方案征集活動中，基于格的密碼方案占據多數.例如，N?ST 第1 輪64 個方案中的26 個[4]、第2 輪26 個方案中的12 個[5]、第3 輪15 個方案中的7 個[6]以及擬標準化4 個方案中的3個[2]均為基于格構造的密碼方案.我國后量子密碼算法設計競賽獲獎方案共14 個，其中有11 個均為基于格構造的.基于格的方案在設計PKE 和KEM 時主要基于一般格、理想格、模格和NTRU 格.常用的格困難問題主要分為2 類：第1 類是{R,M}LWE/LWR 問題[7-10]；第2 類是NTRU 格相關問題[11-13].

NTRU 最早由Hoffstein 等人[14]于1996 年美密會討論環節中提出，但它在1997 年遭遇格攻擊[15].隨后Hoffstein 等人對方案安全性方面進行補救，并于1998 年正式提出NTRU 加密方案（NTRU-HPS）[11].該方案是第1 個基于格困難問題構造的現實的公鑰加密方案.NTRU 相關問題目前已經是許多密碼方案中的基礎元件[16-18].在N?ST 的后量子密碼方案征集項目中，基于NTRU 格的方案具有舉足輕重的地位.具體而言，Falcon 數字簽名[19]基于NTRU 格構造，且是N?ST 后量子密碼方案標準征集擬標準化的數字簽名之一.另外，在N?ST 第3 輪中，NTRU KEM[20]（包含NTRU-HRSS 和NTRUEncrypt）是4 個決賽KEM 方案之 一，NTRU Prime KEM[21]（包 含SNTRU Prime 和NTRU LPRime）是5 個候選方案之一.盡管目前N?ST 選擇了基于模格的Kyber[22]作為唯一的擬標準化KEM方案[2]，而基于NTRU 格的方案沒能被N?ST 選為擬標準化KEM 方案，但N?ST 官方報告聲稱如果Kyber相關專利問題未能得到很好地解決，仍可能會放棄Kyber 而啟用NTRU KEM[23].另外，在2011 年NTRUEncrypt 方案便已入選X9.98 標準并應用于金融服務企業之中[24].自2022 年4 月起，國際標準OpenSSH更新了版本9.0 之后，OpenSSH 便采用了NTRU Prime KEM 方案結合X25519 ECDH 方案的混合模式，以抵抗“先捕獲后解密”攻擊[25].另外，有關基于NTRU 格的方案的研究并不應因此而止步不前，對基于NTRU格的方案的設計和分析理應得到更充分、深入和全面的研究.

基于NTRU 格設計的KEM 備受青睞，主要原因有3 點：1）基于NTRU 格的KEM 具有堅固的安全保障.自NTRU 被提出至今，有關NTRU 的攻擊和密碼分析對基于NTRU 格的KEM 安全性產生的影響非常有限.事實上，大多數基于NTRU 相關困難問題設計的密碼方案至今沒被攻破.2）有關NTRU 的專利已失效.在1997 年，NTRU 加密系統獲得了專利，但在2017 年NTRU 相關核心專利已到期.3）大多數基于NTRU 格的KEM 結構簡單，便于實現，同時加解密算法的運算速度快[20-21].

近些年來，針對基于NTRU 格的KEM 有2 點可優化的方向：

1）計算效率方面.基于NTRU 格的KEM 如NTRUHRSS[20]和SNTRU Prime[21]在計算效率方面遜色于基于{R,M}LWE 的方案.主要是因為后者能夠使用高效的數論變換（number theoretic transform，NTT）來計算多項式乘法.近些年來，文獻[26-27]基于NTT 友好的多項式環來構造出基于NTRU 格的KEM，使得方案中的多項式運算得到高效計算.

2）密文尺寸方面.降低密文尺寸對網絡協議，如TLS 和?oT 資源受限設備通信都具有積極的作用.盡管密文壓縮在基于LWE 及其變體的KEM 中是一項成熟的技術，但對基于NTRU 格的KEM 來說，目前相關研究極少.常見的NTRU 的加密方案的密文形式一般為c=phr+mmodq，其中h為公鑰（一般h=g/f），q為方案模數，g、f為秘密多項式；r為采樣得到的秘密多項式，m為待加密的明文，p為明文空間模數.這可視為m通過編碼到密文c的低位.解密算法將c乘以私鑰f，得到cfmodq=pgr+mf.隨后通過乘f的逆，或當f=pf′+1 時可通過模p消除雜項來恢復明文.這種解密機制要求被消除的雜項為p的倍數.所以一旦密文c被壓縮，壓縮帶來的誤差往往集中在c的低位，從而破壞m的有效信息，此時便無法正確解密得到原始的m.

文獻[28-29]對基于NTRU 格的KEM 的密文壓縮進行了探索，但是文獻[28-29]的方案有2 點不足.第1 點不足是這些方案都基于2 種困難性假設來構建KEM.其中文獻[28]是基于NTRU 假設[11]和RLWE 假設[9]，文獻[29]是基于NTRU 假設和RLWR假設[8].引入過多的困難性假設會導致方案建立在更理想化的假設上.同時，分析這些方案的安全強度則需要分析2 種困難性問題的安全強度，并取2 個安全強度的最小值.所以，方案的安全性很大程度上取決于安全強度更低的困難性問題.NTRU 相關困難問題的安全性經過20 多年的密碼分析現今仍然安全；RLWE 和RLWR 是較之更新的問題而需要進一步密碼分析和驗證.為得到更為穩定的安全保障，僅基于NTRU 相關困難問題設計的KEM 值得深入地研究和探索.第2 點不足是文獻[28-29]的方案均使用糾錯碼和復雜的糾錯機制來恢復明文信息.其中文獻[28]使用可尺度E8格糾錯碼；文獻[29]使用改進的Babai算法.盡管糾錯碼具有良好的糾錯能力從而有效恢復信息，但是KEM 使用糾錯碼會帶來2 個缺點：1）糾錯碼增加了方案遭遇側信道攻擊的風險[30]，特別是計時攻擊[31]；2）糾錯碼導致實現更復雜、更耗時，且更容易出錯.為了設計更安全且便于實現的KEM，設計者應該避免使用糾錯碼.所以，對基于NTRU 格的KEM 來說，在不使用糾錯碼的情況下，如何得到可壓縮密文的構造依然需要進一步探索.

在我國，后量子密碼被我國科協列為60 個我國亟待解決的重大科技難題之一.盡管我國2019 年密碼算法設計競賽的獲獎方案大多數是基于格構造的，且包含基于NTRU 格的FatSeal 簽名[3]，但是在它們之中并沒有基于NTRU 格的PKE 和KEM.在當前國內外網絡空間安全愈發重要的大背景下，我國研究團隊理應自主研制高性能、多樣化的后量子密碼方案.考慮到基于NTRU 格的方案在國際上（特別是N?ST后量子密碼標準征集項目）的重要地位，本文主要關注基于NTRU 格構造高效的PKE 和KEM，并針對目前可優化方向，如計算效率方面和密文尺寸方面，提出一套基于NTRU 格構造的可壓縮密文的實用化公鑰密碼系統.本文旨在為后續同類后量子密碼方案的研究和優化提供重要參考.同時，這方面的研究工作對我國未來的后量子密碼標準的選拔、制定、推廣和實際應用都具有重要的現實意義.

本文的貢獻主要有4 點：

1）基于NTT 友好環 Zq[x]/(xn-xn/2+1)構造了一個基于NTRU 格的可壓縮密文的密鑰封裝方案LTRU.該方案包含了?ND-CPA 安全的公鑰加密方案LTRU.PKE 和?ND-CCA 安全的密鑰封裝方案LTRU.KEM.本文的LTRU 僅基于NTRU 單向困難性假設構建.LTRU 能夠避免引入過多假設，從而避免方案假設過強和過于理想化.同時LTRU 不使用糾錯碼，從而實現更簡單，且降低了遭遇側信道攻擊的風險.已知LTRU 是第1 個僅基于NTRU 類型假設且不使用糾錯碼也能壓縮密文的密鑰封裝方案.

2）提供了針對128 b 安全強度的LTRU 參數集.這使得LTRU 不僅達到了目標安全強度（實際上達到129 b 量子安全強度），還具有與安全性匹配的、可忽略的錯誤率（2-154），同時通信帶寬小于其他NTRU方案.具體而言，與N?ST 第3 輪決賽方案NTRUHRSS 相比，LTRU 的經典安全強度和量子安全強度分別增強6 b 和5 b，并且LTRU 的公鑰尺寸降低14.6%，密文尺寸降低26.0%，總帶寬降低20.3%.

3）提出了一種高效的混合基NTT 算法.該算法能夠有效計算環 Z2917[x]/(x648-x324+1)上的多項式運算，利用3 次單位根的性質來有效減少基-3 FFT trick步驟中一半的乘法數量，并利用1-迭代Karatsuba 算法來有效減少點乘中的乘法數量.通過具體實現的效率分析可知，跟未使用1-迭代Karatsuba 算法和單位根的性質優化乘法數量的NTT 算法相比，本文NTT 在正向變換、點乘和逆向變換的CPU 周期數分別降低24.9%，20.6%，26.8%，總共降低25.3%.

4）提供LTRU 的C 實現和AVX2 實現.實驗結果表明，與NTRU-HRSS 的AVX2 實現相比，LTRU在密鑰生成和解封裝算法上分別快了10.9 倍和1.7倍，封裝算法的速度則與NTRU-HRSS 的速度相當.

1 相關工作

近些年來，陸續有基于NTRU 格的方案被提出.Stehlé等人[32]基于2 次冪分圓環 Z[x]/(xn+1)（其中n為2 次冪）來設計基于NTRU 變體的PKE，并證明了公鑰的安全性.隨后，Wang 等人[33]將該方案推廣至任意的分圓環.但是這2 個方案因為公鑰尺寸過大而無法應用于實際的場景中.Jarvis 等人[34]將NTRUHPS 推廣至Eisenstein 整數環 Z[ω]/(xn-1)（其中ω=exp(2π i/3)）.該方案在密鑰尺寸和性能方面比NTRU-HPS 更有優勢.Hülsing 等人[35]全面提升NTRUHPS 的密鑰尺寸、密文尺寸和效率，并提出了NTRUHRSS.NTRU-HRSS 曾是N?ST 后量子方案征集項目第3 輪決賽方案之一[20].Bernstein 等人[36]考慮到NTRU 類型方案使用的多項式環或因豐富的代數結構而遭受相關攻擊，提出了使用代數結構更少的環Zq[x]/(xn-x-1)的NTRU 變體方案：NTRU Prime（其中n,q均為素數）.NTRU-prime 曾是N?ST 后量子方案征集項目第3 輪候選方案之一[20].

為了追求更高的實現效率，Lyubashevsky 等人[26]在多項式環 Z7681[x]/(x768-x384+1)上構造了針對128 b安全強度的NTTRU 方案.隨后，Duman 等人[27]將該方案推廣至更一般的n并選擇對應的q.但是這些方案均是遵循傳統NTRU 的框架，并不能對密文進行壓縮.

Fouque 等人[29]提出BAT 方案.BAT 與傳統NTRU類型的KEM 的構造有所區別，但與Falcon 數字簽名方案[19]有眾多相似之處.BAT 的私鑰是一組陷門基，這一點與Falcon 相似，但區別于其他NTRU 類型KEM 的私鑰f.直觀地理解，BAT 使用的糾錯碼機制相當于對含有2 個未知數的方程求解出秘密多項式和噪音多項式，并用來恢復明文.BAT 通過將密文構造為RLWR 實例的方式來降低密文的尺寸.然而，為生成陷門基作為私鑰，BAT 的密鑰生成算法速度比常見的NTRU 類型KEM 的速度慢約1 000 倍.其次，為降低密文尺寸而構造的RLWR 實例使用二元的秘密分布（即秘密多項式的系數選自{0,1}），而關于該問題的安全性目前還是公開問題且還需要進一步研究.另外，BAT 缺少匹配128 b 安全強度的參數集，因為它使用2 次冪分圓環 Z[x]/(xn+1)，且n=512和n=1 024，而前者的安全強度略低于128 b，后者的安全強度則遠高于128 b.

2 預備知識

本節主要介紹一些符號說明、基本定義和密碼原語等.

2.1 符號說明和基本定義

1）本文記 Z 為整數環，n和q為 某些整數.定 義集合Zq=Z/qZ ?{0,1,…,q-1}.對 于實數x∈R，符 號表示對x四舍五入后的值.本文主要使用分圓多項式環 R:=Z[x]/(xn-xn/2+1) 及其商環Rq:=R/qR=Zq[x]/(xn-xn/2+1)，其中n=2i3j，i≥0，j＞1，且此時xn-xn/2+1是 3n階分圓多項式.環 R（或 Rq）中的元素均是多項式，本文使用符號f的冪級數形式（或fi∈Zq）.一個函數 ε:N →[0,1]是可忽略的，指的是對任意的正數c以及充分大的 λ，ε(λ)＜1/λc成立.

2）模約減.對于某正整數q，符號r′=rmodq表示r落在 [0,q)∩Z 中的代表元r′.符號r′=rmod±q表示r落在中的代表元r′.另外，符號r′≡rmodq′表示r′和r模q同余.

3）元素的范數[37].對于元素v∈Zq，定義它的?∞范數 ‖v‖∞為 ||vmod±q||.對于環 R（或 Rq）中的元素w，它的 ?∞范數為

4）壓縮函數和解壓縮函數[37].對于正整數q和d，定義壓縮函數

以及解壓縮函數

且對于任意的x∈Zq，有

5）集合和分布.對于集合D，記x←$D表示從D中均勻隨機選 取x.如果D是一個概率分布，x←D表示根據分布D采樣得到x.本文主要使用的分布為：采樣 (a1,a2,…,aη,b1,b2,…,bη)←${0,1}2η，然后輸出根據分布D，采樣多項式f指的是f的每一個系數均根據D采樣得到.

2.2 密碼原語

1）公鑰加密方案

一個公鑰加密方案PKE 包含KeyGen,Enc,Dec3個概率多項式時間（probabilistic polynomial time，PPT）算法，記其明文空間為 M.密鑰生成算法KeyGen輸出公私鑰對 (pk,sk).加密算法Enc輸入公鑰pk和明文m∈M，輸出密文ct.本文在必要時使用Enc(pk,m;coin) 顯式表示加密算法使用的隨機數為coin.確定性的解密算法Dec輸入密文ct和私鑰sk，輸出m∈M，或者 ⊥表示解密失敗.公鑰加密方案的解密錯誤率δ定義為

其中期望作用于 (pk,sk)←KeyGen上，式（1）概率取自加密算法Enc使用的隨機數.一個公鑰加密方案是抗原像恢復意義下的選擇明文PRE-CPA（preimage resistance under chosen-plaintext attacks）安全的[27]，指的是對于任意PPT 敵手 A，其優勢是可忽略的：

一個公鑰加密方案是不可區分意義下的選擇明文?ND-CPA（indistinguishability under chosen-plaintext attacks）安全的，指的是對于任意PPT 敵手 A，其優勢是可忽略的：

2）密鑰封裝方案

一個密鑰封裝方案KEM 包含KeyGen,Encaps,Decaps3 個PPT 算法.記其導出密鑰空間為 K.密鑰生成算法KeyGen輸出公私鑰對 (pk,sk).密鑰封裝算法Encaps輸入公鑰pk，輸出密文ct和密鑰K∈K.確定性的解封裝算法Decaps輸入密文ct和私鑰sk，輸出K∈K，或者 ⊥表示解封裝失敗.密鑰封裝方案的錯誤率 δ定義為Pr[Decaps(sk,ct)≠K:(ct,K)←Encaps(pk)]＜δ，其中概率取自 (pk,sk)←KeyGen和封裝算法Encaps使用的隨機數.一個密鑰封裝方案是不可區分意義下的選擇密文?ND-CCA（indistinguishability under chosenciphertext attacks）安全的，指的是對于任意PPT 敵手A，其優勢是可忽略的：

2.3 NTRU 單向困難性假設

定義1.NTRU 單向困難性假設[12-13].給定NTRU公鑰加密方案的公鑰h以及PPT 加密算法Enc，則NTRU 單向函數是指

其中Enc(h,(r,e)) 指的是以h，e，r作為加密算法的輸入，在NTRU 公鑰加密方案中 Le一般是它的明文空間，Lr一般是它的隨機數空間.

NTRU 單向問題NTRU-OW（NTRU one-wayness）指的是給定公鑰h和密文多項式c，計算得到 (r,e).NTRU 單向問題是困難的，指的是對于任意PPT 敵手A，其優勢是可忽略的：

通俗來講，NTRU 單向困難性假設是指沒有PPT敵手能夠從公鑰h和密文c中恢復出 (r,e).原始的NTRU-HPS 方案[11]便蘊含了NTRU 單向困難性假設，直到文獻[12-13]將NTRU 單向困難性假設提煉出來，并應用在基于NTRU 格的方案（如NAEP 方案）的安全性證明之中.

2.4 ACWC0 轉換

定義2.ACWC0轉換[27].記PKE1=（KeyGen1,Enc1,Dec1）為公鑰加密方案，其明文空間記為 M1.令F :{0,1}*→{0,1}λ為哈希函數，λ為某正整數.ACWC0通過算法1～3 將PKE1=（KeyGen1,Enc1,Dec1）轉換得到另一個公鑰加密方案PKE2=（KeyGen2,Enc2,Dec2），其明文空間為 M2={0,1}λ.

算法1.密鑰生成算法KeyGen2.

根據文獻[27]中的引理2.2 和定理3.3，PKE2方案在隨機預言機模型（random oracle model，ROM）[38]下的?ND-CPA 安全性由定理1 給出.

定理1.在隨機預言機模型下，對于任意的攻擊PKE2的?ND-CPA 安全性的敵手 A，存在攻擊PKE1的PRECPA 安全性的敵手 B，其運行時間與 A相當，使得

另外，根據文獻[27]中的引理2.2 和定理3.4，可得定理2 關于PKE2方案在量子隨機預言機模型（quantum random oracle model，QROM）[39]下 的?NDCPA 安全性.

定理2.在量子隨機預言機模型下，對于任意的攻擊PKE2的?ND-CPA 安全性的量子敵手 A，存在攻擊PKE1的PRE-CPA 安全性的量子敵手 B，其運行時間與 A相當，使得

其中dF是 A 查詢 F的深度.

可見，ACWC0轉換能夠將一個PRE-CPA 安全的公鑰加密方案轉換得到另一個?ND-CPA 安全的公鑰加密方案.本文將在3.1 節中提出的公鑰加密方案便是通過ACWC0轉換得到的.

2.5 數論變換（NTT）

NTT 是快速傅里葉變換（fast Fourier transform，FFT）在有限域上的特殊形式.NTT 是計算高次多項式乘法最高效的算法，其復雜度為O(nlogn)，其中n為被乘多項式的維度.簡單地說，基于NTT 計算多項式乘 法h=fg的過程為h=INT T(NT T(f)?NT T(g))，其中 NT T 表示正向變換，INT T 表示逆向變換，“ ?”表示點乘.本文沿用文獻[40]有關多項式乘法的符號和術語，FFT trick 是計算NTT 的一種快速算法，其計算過程本質是基于多項式環形式的中國剩余定理（Chinese remainder theorem，CRT），即給定兩兩互素的多項式g1,g2,…,gk，有CRT 同構

并且 φ(f)=(fmodg1,fmodg2,…,fmodgk).記 ζ 在Zq中可逆.對于經典的基-2 FFT trick 的情況，有CRT 同構：

其中 ρ是3 次單位根.混合基NTT 指的是在計算NTT過程含有多種FFT trick.

2.6 Karatsuba 算法

定義3.1-迭代Karatsuba 算法[43].設a,b,c,d為 某些數或多項式.1-迭代Karatsuba 算法指的是為了計算t1=ac，t2=ad+bc和t3=bd，可以先計算t1和t3，然 后通過t2=(a+b)(c+d)-t1-t3計算t2.該算法能在增加3 個加（減）法的代價上，減少1 個乘法.

3 本文方案及其分析

下面介紹本文提出的基于NTRU 格構造的可壓縮密文的密鑰封裝方案LTRU.LTRU 包括一個?NDCPA 安全的公鑰加密方案LTRU.PKE，以及一個?NDCCA 安全的密鑰封裝方案LTRU.KEM，其中該KEM通過FO（Fujisaki-Okamoto）轉換[44-45]得到.LTRU.PKE是由底層公鑰加密方案PKE′=（KeyGen,Enc′,Dec′）結合文獻[27]的ACWC0轉換得到的.底層公鑰加密方案PKE′將在3.4 節中展示，但它只能滿足PRECPA 安全性，并且目前還沒有相關文獻論證FO 轉換將PRE-CPA 安全的公鑰加密方案轉換得到?NDCCA 安全的KEM 的規約上界.本文通過增加ACWC0轉換，將底層公鑰加密方案PKE′轉換得到?ND-CPA安全的LTRU.PKE，然后便能通過FO 轉換得到?NDCCA 安全的KEM.

3.1 LTRU 的構造

LTRU.PKE 的具體構造見算法4～6.記其明文空間為 M={0,1}λ，其中 λ 為正整數.記多項式環為Rq=Zq[x]/(xn-xn/2+1)，其中n和q是環參數.記d和p為 正整數，且p和q互素.需要說明的是，在算法4～6 中，為了給出一般的構造框架，本文使用的分布 ψ 泛指 R上的某分布，但事實上，在3.3 節的具體參數選擇方面，本文實例化 ψ 為參數 η=2 的分布（定 義見2.1 節）.令F :{0,1}*→{0,1}λ為哈希函數.本文主要考慮p=2以及 λ=256 的情況.可 視 {0,1}n中的元素是維度為n、系數為0 或1 的多項式.壓縮函數Compress和解壓縮函數Decompress的具體計算過程見2.1 節.

算法4.密鑰生成算法LTRU.PKE.KeyGen.

可見，LTRU.PKE 應用了ACWC0轉換[27]，見算法5 行③以及算法6 行③.LTRU.KEM 是由LTRU.PKE通過轉換得到，其中是文獻[45]提出的FO轉換的一個變體.LTRU.KEM 的密鑰生成算法KeyGen與LTRU.PKE 的KeyGen相 同.LTRU.KEM 的封裝算法和解封裝算法分別見算法7 和算法8.記K為LTRU.KEM 的導出密鑰空間，為方便起見，本文令K={0,1}256.記 COINS為LTRU 公鑰加密方案中加密算法所使用的隨機數空間.記H :{0,1}*→K×COINS為哈希函數.實際上，H能夠拆分為2 部分 H1和 H2，記 H1為 H 映射到 COINS 的部分，H2為 H 映射到K的部分.在算法7 的行②中可以先使用 H1生成coin，在行③中計算得到密文c之后，再使用 H2生成共享密鑰K.

算法7.封裝算法LTRU.KEM.Encaps.

算法8.解封裝算法LTRU.KEM.Decaps.

3.2 錯誤率分析

則LTRU 的錯誤率為 δ.

證明.

從2.1 節的壓縮函數Compress和解壓縮函數Decompress的定義可知，算法6 行①的c′可以表示為

由于LTRU 中h=g/f和f=2f′+1，則可得

本文計算錯誤率的方法論和Python 腳本源自文獻[22,26,37].值得注意的是，文獻[26]將環Z[x]/(xnxn/2+1) 上的多項式的乘積的系數視為由n/2個形如ab+b′(a+a′) 的元組構成，其中a,a′,b,b′的分布由被乘多項式的分布決定.盡管該環上的多項式的乘積另外還包含形如ab+a′b′的元組，文獻[26]建議全部使用ab+b′(a+a′)的形式，因為該形式具有更寬泛的分布，且能得到更保守估計的錯誤率結果.

3.3 參數選擇

本節給出LTRU 的推薦參數集，其主要針對128 b安全強度，如表1 所示.Rq是多項式環，維數n和模數q是環參數.本文選擇NTT 友好的q，旨在q允許在Rq上執行高效的多項式乘法和除法，具體細節見第4 節.p是明文空間模數；d是壓縮參數；ψ是概率分布，本文主要考慮分布即參數為 η=2 的分布，的定義見2.1 節；|pk|，|ct|，B.W.分別是公鑰尺寸、密文尺寸和帶寬（公鑰尺寸+密文尺寸），單位均為B；Sec-（C,Q）是該參數集的NTRU 安全強度（單位為b），C 表示經典安全強度，Q 表示量子安全強度，安全強度的分析見3.5 節；δ是該參數集的錯誤率，其細節見3.2 節.

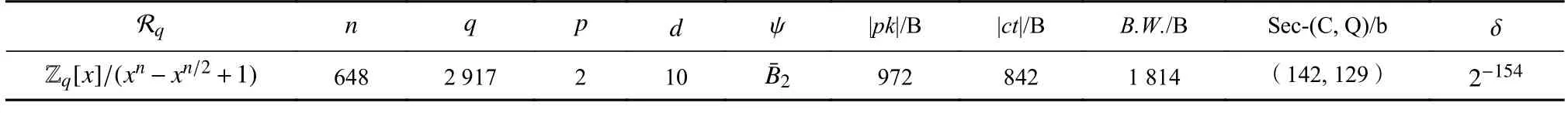
Table 1 Recommended Parameter Set of LTRU表1 LTRU 的推薦參數集

3.4 安全規約

下面將基于NTRU 單向困難性假設，證明LTRU.PKE 是?ND-CPA 安全的.

定理4.?ND-CPA 安全性.對于任意的概率多項式時間敵手 A，存在概率多項式時間敵手 B，其運行時間與 A相當，使得：

證明.LTRU.PKE 方案由底層公鑰加密方案PKE′=（KeyGen,Enc′,Dec′）結合文獻[27]的ACWC0轉換得到，其中底層公鑰加密方案PKE′的KeyGen算法與LTRU.PKE 方案的一致，Enc′算法和Dec′算法分別見算法9 和算法10.

算法9.加密算法PKE′.Enc′.

算法10.解密算法PKE′.Dec′.

由定理1 和定理2 可知，當底層公鑰加密方案PKE′滿足PRE-CPA 安全性時，經過ACWC0轉換得到的LTRU.PKE 方案滿足?ND-CPA 安全性.下面將通過Game-Hopping 技術[46]來證明底層公鑰加密方案PKE′的PRE-CPA 安全性.

記 A 是攻擊PKE′方案的PRE-CPA 安全性的概率多項式時間敵手.考慮游戲G0和G1.記事件S ucci為敵手 A 在游戲Gi中獲勝，即游戲Gi的輸出滿足c=c*.

游戲G0是 關于PKE′方案原始的PRE-CPA 游戲.根據PRE-CPA 安全性的定義，可知

游戲G1是在游戲G0的基礎上，取消對行⑦挑戰密文c*的壓縮操作.所以，敵手 A 在游戲G1中擁有的挑戰密文的信息至少比在游戲G0中的多.可見，游戲G0的困難性至少與游戲G1的相同，則

整合游戲G0和G1中的概率可知，對于概率多項式時間敵手 A，存在概率多項式時間敵手 B，使得

再根據定理1 和定理2，由PKE′方案的PRE-CPA 安全性可得到LTRU.PKE 的?ND-CPA 安全性，其對應的規約上界正如定理4 所示.綜上，命題得證.證畢.

從定理4 可知，若NTRU 單向困難性問題是困難的，那么LTRU.PKE 是?ND-CPA 安全的.由于LTRU.KEM 是從?ND-CPA 安全的LTRU.PKE 通 過變換得到，根據文獻[45,47]，LTRU.KEM 在經典隨機預言機和量子隨機預言機下的?ND-CCA 安全性由定理5給出.

定理5.?ND-CCA 安全性[45,47].在記 γ 和 δ分別是LTRU.PKE 的弱spread 參數[45,47]和解密錯誤率.對于任意攻擊LTRU.KEM 的 ?ND-CCA 安全性的概率多項式時間敵手 A，存在攻擊LTRU.PKE 的?ND-CPA安全性的概率多項式時間敵手 B，使得：

1）在經典隨機預言機模型下，將 H建模為經典隨機預言機，A查詢至多qH次 H，查詢至多qD次解封裝預言機，B的運行時間和 A的相當，則有

2）在量子隨機預言機模型下，A 和 B為量子敵手，且將 H建模為量子隨機預言機，A以量子方式查詢至多qH次 H，以經典方式查詢至多qD次解封裝預言機，則有

其中qT:=2(qH+qD)，并且

3.5 安全強度

對于基于NTRU 格構造的KEM 來說，格攻擊是目前最有效的攻擊.本節主要從常用的格攻擊來分析LTRU 的安全強度.

1）NTRU 格

起初，基于NTRU 格構造的方案均是依賴于多項式環上的困難性問題.然而，Coppersmith 等人[15]提出針對基于NTRU 格構造方案的格攻擊，它的核心思想是構造NTRU 格.本文方案的公鑰對應的NTRU格L(B)?Z2n的基矩陣為

其中In是n維單位矩陣，Rot(h)是h的循環移位矩陣，即它的第i行向量對應xihmodxn-xn/2+1.文獻[15]提出，秘密 (f,g) 及其循環移位向量是格 L(B)的最短向量.事實上，NTRU 類型方案的格攻擊流程為：通過格基約化算法求解格 L(B)的唯一最短向量問題（unique-short vector problem，u-SVP），找到該最短向量之后轉化得到方案的私鑰[15].

2）原始攻擊

原始攻擊通過構造一個整數嵌入格，如Kannan嵌入[48]和Bai-Galbraith 嵌入[49]等來求解u-SVP 問題.目前主要的格基約化算法為BKZ 算法[50-51].給定格L(B)的一組基，BKZ 算法運行時將格劃分為多個低維度格，并把這些低維度格的維度記為b.然后在b維格中求解最短向量問題（short vector problem，SVP），所使用的方法有篩法和枚舉.根據文獻[52]的core-SVP 方法論，對于b維格上求解SVP 問題，目前最優的經典算法的復雜度為 20.292b，最優的量子算法的復雜度為 20.265b.core-SVP 方法論將這些復雜度視為求解b維格SVP 問題的復雜度，并將得到的BKZ 算法的復雜度作為原始攻擊的復雜度估計.本文將基于core-SVP 方法論給本文方案提供一個保守估計的安全強度，并基于文獻[22,37,52]提供的計算安全強度的Python 腳本來計算LTRU 在原始攻擊下的經典安全強度和量子安全強度，其詳細結果如表1 所示.

3）其他攻擊

對偶攻擊主要通過將判定型LWE 問題規約為短整數解問題（short integer solution problem，S?S）的方式來求解判定型LWE 問題.由于對偶攻擊不適用于NTRU 類型的方案[53]，故本文不考慮對偶攻擊對LTRU的影響.過度拉伸NTRU 攻擊[54]的適用范圍為模數q遠大于秘密多項式系數的情況.由于LTRU 的模數q數值較小，不滿足該情況，故本文不考慮該攻擊.混合攻擊[55]是格攻擊和中間相遇攻擊的提升版本，但混合攻擊對于有著稀疏分布的秘密多項式系數和噪音多項式系數的方案能取得顯著效果.然而對于LTRU，混合攻擊不如原始攻擊有效，因為LTRU 的秘密 (f,g)并非稀疏分布，不符合混合攻擊的條件.

3.6 分析和討論

1）多項式環

本文LTRU 方案使用第 3n個分圓多項式環Zq[x]/(xn-xn/2+1)，其中n的形式為 3l×2e，q為某些素數.主要原因是，當選擇合適的q，如NTT 友好的q時，存在高效的NTT 算法計算該環上的多項式乘法和除法.同時，n的選擇具有更大的靈活性，因為n能夠選擇576，768，864，972，1 152，1 296 等數值.當選擇其他的n值時，LTRU 能夠達到其他的安全強度（如192 b和256 b），而不再局限于128 b 的安全強度.但是，本文主要針對128 b 的安全強度，故選擇n=648.相比而言，NTRU-HRSS[20]使用多項式環 Zq[x]/(xn-1)，其中n為素數，q為2 次冪；SNTRU Prime[21]使用多項式環Zq[x]/(xn-x-1)，其中n，q均為素數.這些多項式環不是NTT 友好環，所以這些多項式環上的多項式乘法和除法更復雜，且耗時更多.

2）明文空間模數p

與其他NTRU 方案如文獻[20-21,26-27]中的方案不同，本文LTRU 使用的明文空間模數p=2，且只需出現在私鑰f中，即f=pf′+1，而無需在公鑰h以及解密算法中出現.但是，NTRU 方案[20-21,26-27]使用模數p=3.甚至，由于NTRU 類型方案要求q和p互素，而NTRU-HRSS[20]由于使用2 次冪的模數q，所以它使用了與q互素的最小整數p=3.

3）糾錯機制

常見的NTRU 類型方案[20-21,26-27]的密文形式為c=phr+mmodq，這可以視為明文m編碼在密文c的低位.其恢復明文m的方式主要通過計算cfmodq之后再模p來消去雜項.這種糾錯機制依賴于雜項是p的倍數.與之不同的是，LTRU 在底層公鑰加密方案PKE′中首先將明文m提升q/2 倍，相當于把明文m編碼到密文c的高位，隨后在解密算法中只要求雜項的范數小于 1/2，而不必要求其為p的倍數.同時可以看到，LTRU 不使用糾錯碼來恢復明文.糾錯碼雖然能夠高效地實現糾錯來恢復明文，但是糾錯碼使得代碼實現更復雜且增加遭遇側信道攻擊的風險，如文獻[30]針對糾錯碼提出了有效的側信道攻擊.

4）密文壓縮

LTRU 的密文壓縮操作見算法5 的行②.本文的LTRU 是第1 個僅基于NTRU 單向困難性假設構造的、不使用糾錯碼也能夠壓縮密文的密鑰封裝方案.LTRU 的密鑰壓縮參數d可根據需求自行調整.對于其他NTRU 類型方案[20-21,26-27]，如果它們壓縮密文，那么壓縮過程會在密文的低位帶來誤差，而編碼在密文低位的明文m的有效信息會被這些誤差破壞，使得正確的明文m難以恢復出來；同時在解密算法中雜項也不再是p的倍數，所以也無法通過模p來消去雜項以恢復正確的明文m.

4 高效的混合基數論變換

本節將介紹本文提出的一種混合基NTT 算法，其能高效地計算本文推薦參數集LTRU-648 所使用的 環 Zq[x]/(xn-xn/2+1)，n=648，q=2 917上的多項式乘法和除法，且利用了1-迭代Karatsuba 算法和單位根的性質減少乘法的數量，以提高計算效率.

對于 Zq[x]/(xn-xn/2+1)，n=648，q=2 917，可 知Zq中存在 3n/2 次本原單位根 ζ=2，其中ζ為k次本原單位根是指ζk≡1modq且ζi≠1modq，0＜i＜k.

4.1 正向變換

為方便理解，圖1 展示了混合基NTT 對應的CRT 同構樹形圖.本文的混合基NTT 的計算過程主要依靠逐層CRT 分解.

Fig.1 The tree map of CRT isomorphism圖1 CRT 同構的樹形圖

類似于文獻[26]提出的第1 層CRT 同構，對于Zq[x]/(xn-xn/2+1)，有

其中 ζ1+ζ2=1 和 ζ1ζ2=1.容易求得，ζ2=1-ζ1和取ζ1=ζn/4modq以 及 ζ2=ζ5n/4modq，對于任意的f∈Zq[x]/(xn-xn/2+1)，可得

由于 ζ1fn/2只需計算1 次而可使用2 次，故式（2）（3）總計只需n/2 個乘法和n個加（減）法.

1）基-2 FFT trick 步驟

可利用CRT 對 Zq[x]/(xn/2-ζ1) 和 Zq[x]/(xn/2-ζ2)進行基-2 FFT trick 步驟的分解.對于每個基-2 FFT trick步驟形如

其中r為 ζ 的某次冪，對于f′∈Zq[x]/(x2m-r2)，可得

其中每個r fi′只需計算1 次而可使用2 次.這使得每層的基-2 FFT trick 步驟所需乘法數量從n個銳減到n/2個.

2）基-3 FFT trick 步驟

對于n=648，基-2 FFT trick 步驟可進行1 層，直至得到4 個形如 Zq[x]/(x162-ζ81)的項.此時本文采用基-3 FFT trick.每個基-3 FFT trick 步驟均形如

其中r為 ζ 的某次冪，ρ=ζn/3modq為3 次單位根.Zq[x]/(x3m-r3) 中的多項式f′′可以表示為

其中fa,fb,fc均為m-1 次多項式.由于 ρ3=1 modq，可得

注意到ρ2+ρ+1=0 modq，則 ρ2=-ρ-1 modq.類似于文獻[56]，此時有

以及

于是可得

注意到，r fb,r2fc,ρ(r fb-r2fc)都只需要計算1 次而能夠多次使用.并且只需存儲和使用本原單位根r和r2以及3 次單位根 ρ，而無需存儲其他值如 ρr，ρ2r2，ρ2r，ρr2.易知，使用3 次單位根的性質之后，每層的基-3 FFT trick 步驟所需乘法數量從 2n個銳減到n個.

正向變換中基-3 FFT trick 步驟可進行4 層，直到將Zq[x]/(xn-xn/2+1) 分解得到n/2個模2 次多項式的環.換句話說，即有

其中 τ(i) 表示第i個環中 ζ的冪且序號從0 開始.對于f∈Zq[x]/(xn-xn/2+1)，其正向變換的結果記為

為方便后文書寫，本文使用符號 NT T表示上述的正向變換過程.正向變換 NT T的偽代碼見算法11.

算法11.正向變換 NT T.

4.2 逆向變換

逆向變換可由正向變換的逆過程得到.本文使用符號 INT T表示逆向變換.值得注意的是，在計算基-3 逆向FFT trick 時，同樣可利用3 次單位根的性質減少乘法的數量.沿用4.1 節的符號和Zq[x]/(x3m-r3) 示例，在基-3 逆向FFT trick 中，從fx,fy,fz計算得到f′′.由f′′=fa+fbxm+fcx2m可知，這等價于得到fa,fb,fc.先計算

利用ρ2=-ρ-1 modq，進一步可得

以及

于是可得

其中倍數 3-1可延遲處理.故易知，基于3 次單位根的性質，每層的基-3 逆向FFT trick 步驟所需乘法數量從 2n個銳減到n個.

另外，對于基-2 逆向FFT trick，在此沿用4.1 節的示例，從fl=f′modxm-r和fr=f′modxm+r計算得到f′∈Zq[x]/(x2m-r2)的步驟為

其中fl,i和fr,i分別表示fl和fr的第i個系數，倍數 2-1同樣可延遲處理.易知，每層的基-2 逆向FFT trick 步驟共需要n/2個乘法.再合計上基-3 逆向FFT trick 步驟延遲處理的倍數，在整個逆向變換結束之時，需要乘以總的倍數 (n/2)-1modq.

逆向變換 INT T 的偽代碼見算法12.

算法12.逆向變換 INT T.

4.3 點 乘

原本需要5 個乘法，現在只需要4 個乘法.使用1-迭代Karatsuba 算法計算點乘的偽代碼見算法13.

算法13.點乘.

4.4 基于混合基NTT 的多項式運算

基于混合基NTT 計算多項式乘法h=fg∈Zq[x]/(xn-xn/2+1)的過程為

另外，本文同樣使用該混合基NTT 計算多項式除法h=g/f∈Zq[x]/(xn-xn/2+1)，即計算LTRU 方案中的公鑰h.具體而言，其計算過程為

算法14.計算低次數多項式的逆.

5 實現細節

本文給出了LTRU 的便攜C 實現和優化AVX2實現.下面將簡要介紹LTRU 的一些實現細節.值得注意的是，LTRU 的所有實現均采用了常數時間實現技巧，以抵抗一些潛在的側信道攻擊，特別是計時攻擊[31].

5.1 基本構件

本文使用的模數q=2 917是低于16 b 的素數，所以Zq[x]/(xn-xn/2+1) 中的多項式能夠使用長度為n、類型為16 b 有符號整型的數組來存儲.

1）哈希函數

本文中使用的哈希函數均使用SHA3 系列函數來實例化.具體而言，使用SHA3-256 實例化哈希函數 F，使用SHA3-512 實例化哈希函數 H.其中 H以明文消息m作為輸入，得到64 B 的輸出，其中前32 B 作為導出的共享密鑰，后32 B 作為種子并使用SHAKE128 來生成加密算法所需的隨機數.

2）秘密多項式

本文使用的秘密多項式如f′,g,r都是根據分布采樣得到.每采樣一個系數需要4 個隨機比特，所以采樣一個多項式需要 4n個比特，即n/2字節.

3）約減算法

在計算多項式系數的加法和乘法時，計算結果存在超出16 b 有符號整型的有效表示范圍的可能性.此時需要使用約減算法將計算結果約減到 [0,q).本文使用Barrett 約減算法[57]和Montgomery 約減算法[58].其中Barrett 約減算法主要用于系數加法后的約減；而Montgomery 約減算法主要用于系數和系數相乘，或者系數和本原單位根相乘時的約減.

4）消息的存儲形式

注意到在LTRU 加密算法中，多項式e是系數范圍取自 {0,1} 的多項式，所以可以將e視為大小為n的比特串.實際上，本文使用n/8 個字節（即n位）來存儲并表示e，這樣能夠減少將e在多項式和比特串之間轉換的過程，提高效率.

5）公私鑰和密文

5.2 C 實現

本節提供LTRU 的C 實現的細節.本文使用第4節的高效的混合基NTT 來計算LTRU-648 的多項式乘法和除法（即計算公鑰h）.測試設備為：硬件配置為2.3 GHz 的?ntel?Core? i7-10510U CPU 和16 GB 內存的筆記本電腦，且關閉Turbo Boost 和Hyperthreading.操作系統為：核為Linux Kernel 4.4.0 的Ubuntu 20.04 LTS 操作系統，且gcc 版本為9.4.0.編譯參數為：-Wallmarch=native-mtune=native-O3-fomit-framepointer-Wnounknown-pragmas.

本文LTRU 的C 實現只涉及到整型算術操作，特別是16 b 有符號整型算術.在NTT 的實現中，由于C 語言的“%”運算符不是常數時間實現，其執行時間和輸入數據長度密切相關，存在泄露秘密數據的可能性，故本文轉向使用常數時間實現的Barrett約減算法和Montgomery 約減算法.對于正向NTT 變換，本文使用延遲規約策略[59]來減少約減的次數.具體而言，對于乘法中使用的Montgomery 約減，其輸出值范圍為 [-q,q].本文使用的模數q為12 b，所以在6層FFT trick 之后，正向NTT 變換輸出的多項式范圍在 [-7q,7q]之間，這顯然在16 b 有符號整型的有效表示范圍之內.故中間計算過程無需進行額外的Barrett 約減，而只需要在正向NTT 變換結束時進行1 次Barrett 約減.

5.3 AVX2 實現

本節提供LTRU 的AVX2 實現細節.AVX2 實現主要優化的運算包括：多項式加法/乘法/除法、模約減算法等.但是，SHA3 系列哈希函數并沒采用AVX2 優化實現，而是繼續采用C 語言的實現.這是因為SHA3 系列哈希函數難以向量化實現，而目前最高效的實現是基于C 語言的[52].另外，NTT 運算非常耗時，所以NTT 運算是AVX2 優化的主要目標.下面主要介紹本文提出的混合基NTT 的AVX2 實現細節.

AVX2 指令集的載入/存儲指令一次性載入/存儲的數據長度為256 b.換句話說，指令能夠一次性載入/存儲16 個多項式系數，因為每個系數使用16 b 有符號整型表示.但是，每個多項式共有 648個系數，其中648 并非16 的整數倍.為了能夠使用AVX2 指令集的載入/存儲指令，將648 個系數對相鄰的16 個系數進行劃分，得到40 個劃分單位以及剩下的8 個系數，然后對每個劃分單位進行數據對齊.這種方法雖然便于使用載入/存儲指令，但不便于在NTT 運算中計算基-2 FFT trick 步驟和基-3 FFT trick 步驟.

為了方便使用AVX2 指令集的載入/存儲指令，同時方便計算基-2 FFT trick 步驟和基-3 FFT trick 步驟，本文采用2 個系數填充過程：

1）將648 個系數對相鄰的12 個系數進行劃分，得到54 個劃分單位；

2）把每一個劃分單位里面的12 個系數拓展到16 個系數，即保留原12 個系數位置不變，在它們末尾的位置填充4 個0.

通過這2 個系數填充過程，得到864 個系數，以及新的54 個劃分單位，每個劃分單位包含16 個系數.此時每個劃分單位能夠一次性被載入到寄存器之中.在完成寄存器一系列計算、存儲回內存位置后，多項式系數提取的過程為：

1）將864 個系數對相鄰的16 個系數進行劃分，得到54 個劃分單位；

2）在每一個劃分單位中提取前面的12 個系數，舍棄末尾的4 個0.

通過這2 個系數提取過程，得到原始長度的多項式數組.系數填充過程和系數提取過程如圖2 所示.

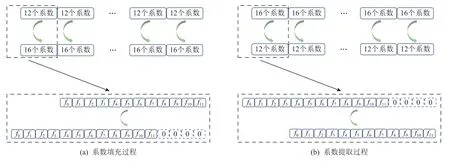
Fig.2 The padding and extraction of coefficients圖2 系數的填充與提取

這種填充過程應用在多項式的NTT 運算，如正向變換、逆向變換、點乘和求逆之中.另外，這種填充過程使得NTT 運算以12 倍的并行度進行計算，區別于通常的16 倍的并行度計算.這是因為此時每個寄存器只能一次性處理原始多項式的12 個系數，而非原始多項式的16 個系數.由于AVX2 指令集的載入/存儲指令耗時較多，所以應該減少內存訪問的次數.常用的方法是合并處理NTT 運算中的若干層.本文合并正向變換的第2 層和第3 層的計算.在此期間，僅需載入一次數據，無需額外的訪問內存和數據載入/存儲便能夠完成第2 層和第3 層的計算，這能夠降低因載入/存儲指令帶來的CPU 周期數的消耗.本文通過vmovdqa指令完成數據的載入/存儲.在分別載入多項式系數和本原單位根之后，通過vpmulhw指令和vpmullw指令分別計算它們乘積的高位和低位，這樣能夠高效地計算它們的Montgomery約減的值.本文的AVX2 實現將一些常用的代碼段通過macro封裝起來，這使得整體代碼簡潔和可讀性強.

5.4 常數時間實現

計時攻擊[31]是一種常見的側信道攻擊，它指的是敵手可以根據密碼方案在軟硬件環境中的執行時間等信息來推斷所執行的運算操作和內容訪問情況，繼而攻擊者可以根據所獲取的側信道信息來推算出該操作所涉及的一些秘密信息，如私鑰或者一些秘密值.目前來說，密碼方案的實現幾乎都需要考慮計時攻擊，并應該采用常數時間實現策略.因此，本文的LTRU 實現過程采用了常數時間實現策略.最重要的是，本文并沒使用非常數時間的指令來操作秘密數據，以及沒使用依賴于秘密數據的判斷分支語句，也沒訪問依賴于秘密數據尋址的內存地址.計算NTT 過程中取模使用到的Barrett 約減算法和Montgomery 約減算法均是常數時間實現[59]，且算法本身對任意合適的模數均成立.至于采樣秘密多項式f′,g,r，本文均以常數時間的方式來采樣.每次固定使用4 b 來生成1 個多項式系數.顯然，生成秘密多項式的時間也是恒定的.

6 比較和分析

本節將比較混合基NTT 算法與未使用1-迭代Karatsuba 算法和單位根的性質優化乘法數量的NTT算法，以及比較本文LTRU 和其他NTRU 類型密鑰封裝方案如NTRU-HRSS[20]，SNTRU Prime[21]，NTTRU[26]，NTRU-A[27]，CTRU[28]，BAT[29]，還有基于模格的密鑰封裝方案如N?ST 標準化方案Kyber[22].

表2 給出了混合基NTT 算法與未使用1-迭代Karatsuba 算法和單位根的性質優化乘法數量的NTT算法在理論乘法復雜度分析和具體實現的CPU 周期數的比較.

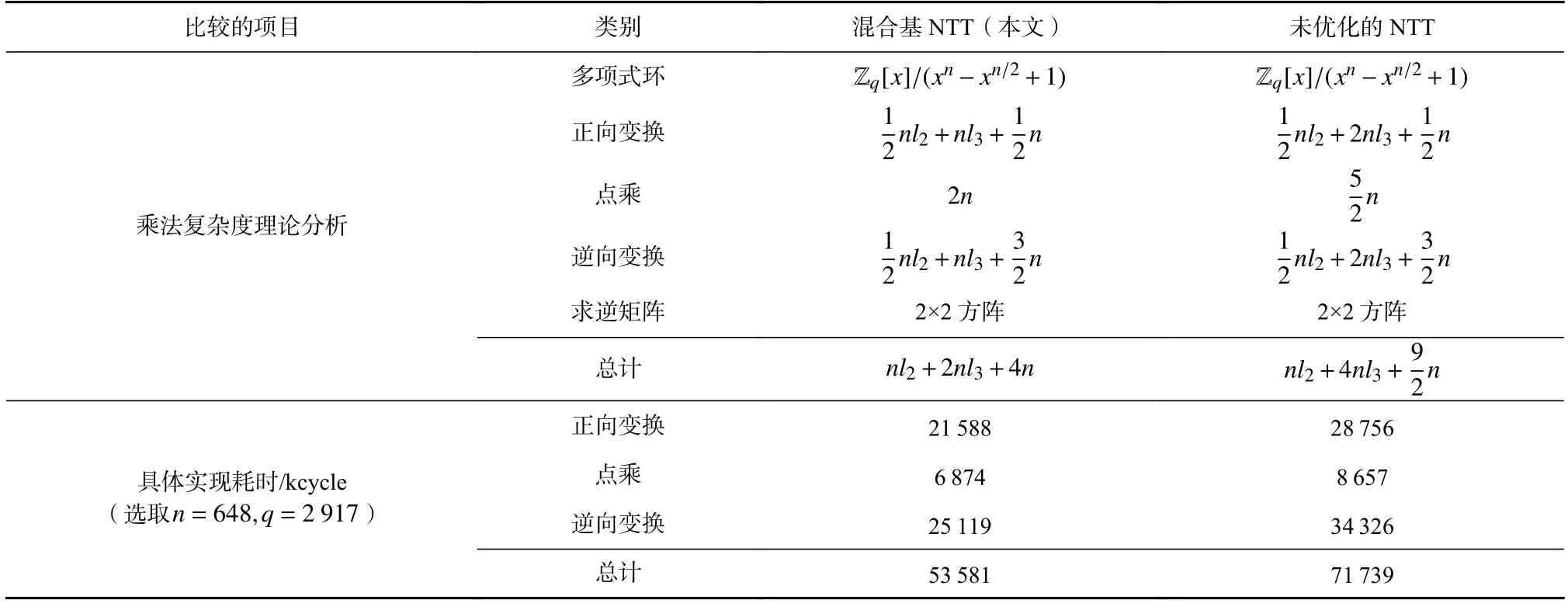
Table 2 Comparison Between Mixed-Radix NTT and Unoptimized NTT表2 混合基NTT 和未優化的NTT 的比較

表3 和表4 展示了本文LTRU 和其他方案對比的詳細情況.為方便比較，在此選取與這些方案安全強度接近的參數集，但CTRU 和Kyber 并沒有接近128 b量子安全強度的參數集，所以在此選取它們的推薦參數集.SNTRU Prime 選取SNTRU Prime-761 參數集，NTRU-A 選取參數集，CTRU 選取CTRU-768 參數集，BAT 選取BAT-512 參數集，Kyber 選取Kyber-768 參數集.其中NTRU-HRSS，SNTRU Prime-761，Kyber-768 的數據和開源代碼來自它們的N?ST第3 輪材料.NTTRU 的數據和開源代碼來自文獻[26].的數據來自文獻[27]，CTRU-768 的數據來自文獻[28]，BAT-512 的數據來自文獻[29].

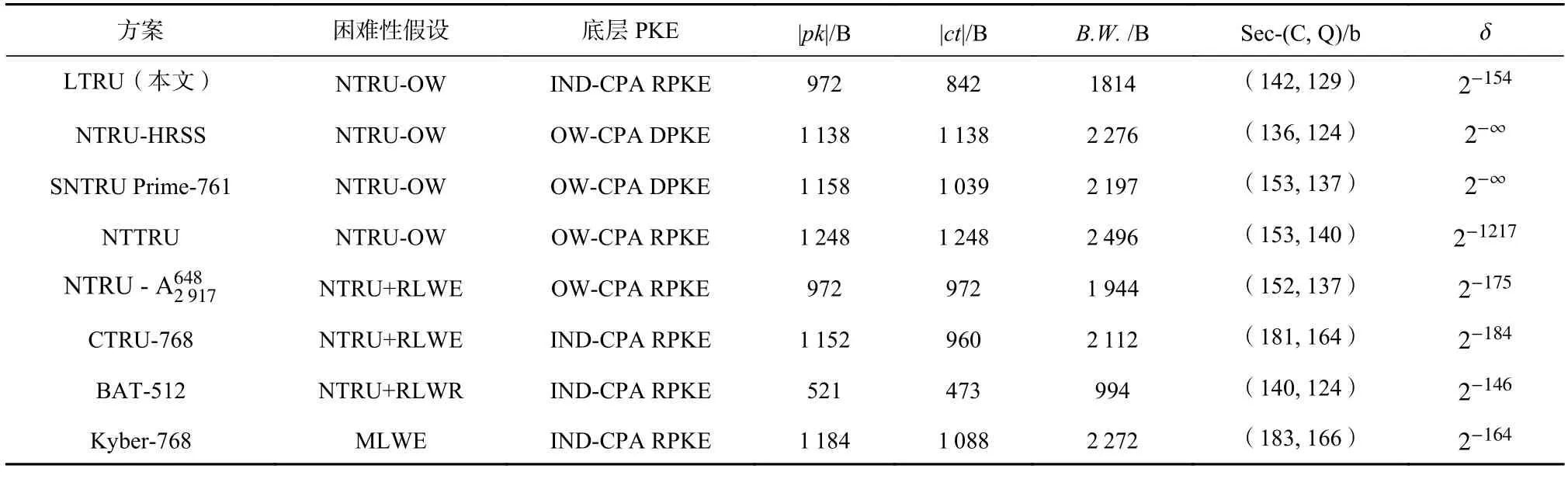
Table 3 Comparison Between LTRU and Other Schemes表3 LTRU 和其他方案的對比

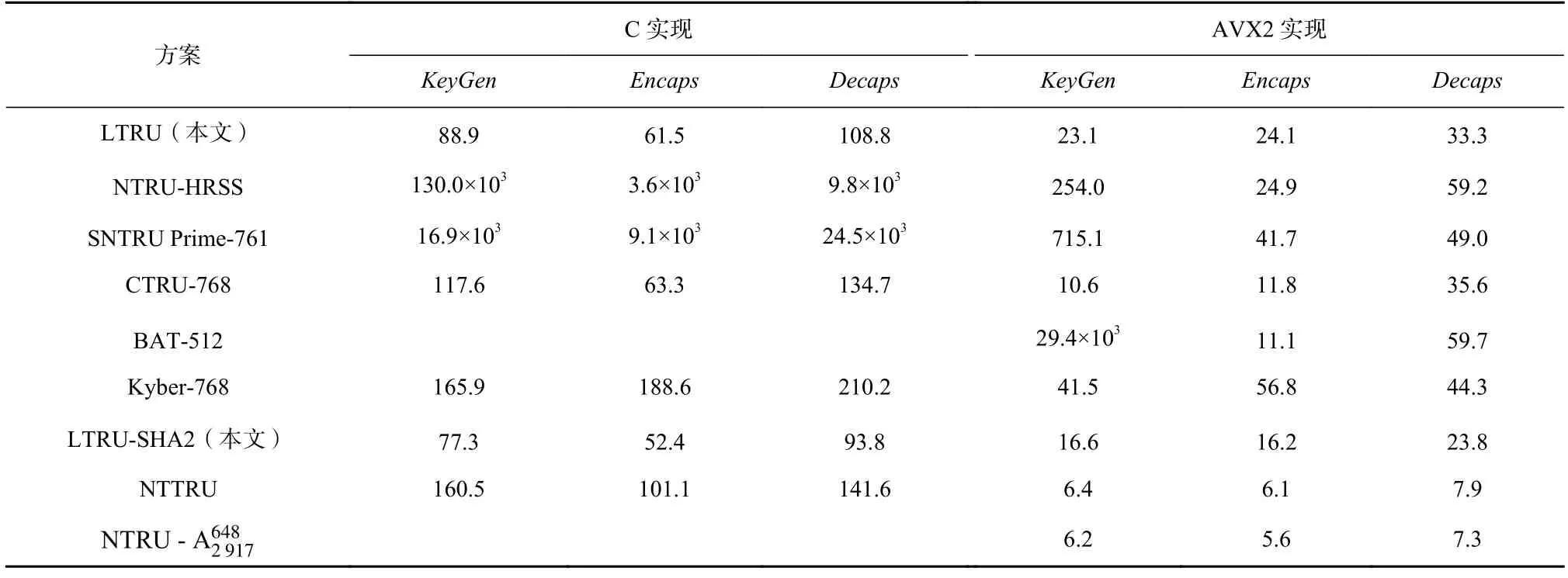
Table 4 Comparison of Implementation Efficiency of Schemes表4 方案的實現效率對比 kcycle

6.1 NTT 算法的比較

值得注意的是，本文的混合基NTT 和未優化的混合基NTT 在多項式環 Zq[x]/(xn-xn/2+1)首層CRT同構具有相同的乘法復雜度：正向變換時需要n/2個乘法，逆向變換時需要 3n/2個乘法.為方便比較乘法復雜度，在此記基-2 FFT trick 和基-3 FFT trick 的層數分別為l2和l3.在本文的混合基NTT 中，每層基-2 FFT trick 的正向變換和逆向變換均需要n/2個乘法.每層基-3 FFT trick 的正向變換和逆向變換均需要n個乘法.然而，未優化的NTT 每層基-3 FFT trick 的正向變換和逆向變換均需要 2n個乘法.因為2 種NTT 算法的求逆運算相同，于是求逆運算具有相同的乘法復雜度，故可以省去對它們的求逆運算的比較.

從表2 可以看出，在比較多項式乘法復雜度時，本文NTT 比未優化的NTT 在正向變換、點乘和逆向變換方面分別減少了nl3，n/2，nl3個乘法，總計減少2nl3+n/2 個乘法.具體而言，選取參數n=648和q=2 917 時，此時層數分別為l2=1,l3=4.測試數據均由C 語言實現，并采用O3 優化指令.從具體實現的CPU 周期數來看，相比未優化的NTT，本文NTT在正向變換、點乘和逆向變換的CPU 周期數分別降低24.9%，20.6%，26.8%，總共降低25.3%.

6.2 方案的性能比較

在表3 中，困難性假設指的是該方案所基于的困難性問題.底層PKE 指的是該密鑰封裝方案所蘊含的底層公鑰加密方案的屬性，其中?ND-CPA 指不可區分意義下的選擇明文安全性，OW-CPA 指單向意義下的選擇明文安全性，DPKE 指確定性的公鑰加密方案，RPKE 指隨機性的公鑰加密方案.|pk|，|ct|，B.W.分別指它們的公鑰尺寸、密文尺寸和帶寬（公鑰尺寸+密文尺寸），單位均是 B.Sec-（C,Q）是方案的安全強度，C 表示經典安全強度，Q 表示量子安全強度.δ指方案的錯誤率.

6.3 方案的效率比較

在表4 中，KeyGen，Encaps，Decaps對應的列分別給出這些密鑰封裝方案在密鑰生成算法、密鑰封裝算法和解封裝算法運行10 000 次的平均CPU 周期，單位是kcycle.

需要說明的是，NTRU-HRSS，SNTRU Prime-761，NTTRU，Kyber-768 的C 實現數據均是將它們的開源C 代碼在同一平臺上運行得到的，旨在為它們的C 實現效率提供直觀的對比.至于NTRU-HRSS，SNTRU Prime-761，Kyber-768 的AVX2 實現的測試數據則是取自SUPERCUP（代號為supercop-20220506，測試設備為3.0GHz ?ntel Xeon E3-1 220 v6）[60]；SUPERCUP能夠提供密碼方案的AVX2 實現最新最快的測試數據.NTTRU 的AVX2 測試數據取自文獻[26].NTRU-的AVX2 測試數據則取自文獻[27]，BAT-512 的AVX2 測試數據則取自文獻[29]，CTRU-768 的C 實現和AVX2 實現的測試數據均是取自文獻[28].需要注意的是，文獻[27-28]沒有提供開源C 代碼和AVX2代碼，文獻[29]只提供AVX2 代碼.且文獻[27,29]只提供AVX2 實現的測試數據，故為公平比較，表4 只展示和BAT-512 的AVX2 實現的測試數據，而不再展示它們的C 實現的測試數據.

6.4 分析和結論

經表3 和表4 的數據分析，與其他基于NTRU 格的密鑰封裝方案NTRU-HRSS[20]，SNTRU Prime[21]，NTTRU[26]，NTRU-A[27]，CTRU[28]，BAT[29]，還有基于模格的密鑰封裝方案Kyber[22]相比，本文的LTRU 具有4 點優勢：

1）小的公鑰尺寸、密文尺寸和帶寬

與NTRU-HRSS，SNTRU Prime-761，NTTRU，CTRU-768，Kyber-768 對比，LTRU 具有更小的密文尺寸和更小的通信帶寬.具體地，與NTRUHRSS 對比，LTRU 的公鑰尺寸降低14.6%，密文尺寸降低26.0%，帶寬降低20.3%.與SNTRU Prime-761 相比，LTRU 的公鑰尺寸降低16.1%，密文尺寸降低19.0%，帶寬降低17.4%.與Kyber-768 相比，LTRU 的公鑰尺寸 降低17.9%，密文尺寸降低22.6%，帶寬降低20.2%.LTRU 和具有相同長度的公鑰尺寸，但是LTRU 的密文尺寸更小，降低了13.4%.由于BAT-512 使用復雜的糾錯碼使得它能使用更小的模數，從而它的帶寬比LTRU 的更有優勢，但復雜的糾錯碼導致它的密鑰生成比LTRU 的密鑰生成慢了3個數量級.

2）均衡的安全強度、錯誤率和帶寬

由于LTRU 的目標安全強度為128 b，所以它的錯誤率 2-154可視為可忽略.NTRU-HRSS 和BAT-512的量子安全強度只有124 b，并沒達到128 b.而Kyber-768 具有166 b 量子安全強度.CTRU-768 具有164 b量子安全強度，與128 b 的間距過大，造成過剩的安全性.SNTRU Prime-761，NTTRU，雖然達到了128 b 安全強度，但其帶寬都比LTRU 的帶寬大.注意到NTRU-HRSS 和SNTRU Prime-761 均為零錯誤率，但是它們需要使用更大的模數q，這無疑增加了通信帶寬.所以，與其他方案對比，LTRU 達到了128 b 安全強度，且具有與安全強度匹配的、可忽略的錯誤率，同時能夠節省通信帶寬.

3）強的底層PKE 方案安全性

由于Kyber-768 是基于MLWE 困難性假設的，而其他方案都是基于NTRU 相關的困難性假設，所以為了公平對比，在此只比較LTRU，NTRU-HRSS，SNTRU Prime-761，NTTRU，CTRU-768，BAT-512 的底層PKE 方案安全性.從表3 可以看到，LTRU，CTRU-768，BAT-512 的底層PKE 方案能夠達到?NDCPA 安全性，而NTRU-HRSS，SNTRU Prime-761，NTTRU，的底層PKE 方案均是OW-CPA 安全的.其中CTRU-768 和BAT-512 均基于2 個困難性假設，唯有LTRU 僅基于NTRU-OW 假設而達到?ND-CPA安全性.不容忽視的是，對底層PKE 方案來說，?NDCPA 安全性比OW-CPA 安全性更強.

4）高效的實現

從表4 可知，LTRU 具有出色的實現效率.具體而言，與NTRU-HRSS 的C 實現相比，LTRU 在密鑰生成、封裝和解封裝等算法上分別快了1 462.3 倍、58.5 倍和90.0 倍；與NTRU-HRSS 的AVX2 實現相比，LTRU在密鑰生成算法和解封裝算法上分別快了10.9 倍和1.7 倍，其封裝算法的速度與NTRU-HRSS 的相當.另外，與SNTU Prime-761 的AVX2 實現相比，LTRU 在密鑰生成、封裝和解封裝等算法上分別快了30.9 倍、1.7 倍和1.4 倍.主要原因是LTRU 使用了本文提出的高效的混合基NTT 計算多項式運算，而NTRUHRSS 和SNTU Prime-761 使用的多項式環不是NTT友好的，它們只能使用效率更低的算法計算多項式運算.與CTRU-768 相比，LTRU 的C 實現在密鑰生成、封裝和解封裝等算法都更有優勢，AVX2 實現在解封裝算法的速度與CTRU-768 的相當.與BAT-512 的AVX2 實現相比，LTRU 在密鑰生成算法上快了3 個數量級，在解封裝算法上快了1.7 倍.

與Kyber-768 相比，LTRU 的實現效率全面占優.具體而言，與Kyber-768 的AVX2 實現相比，LTRU 在密鑰生成、封裝和解封裝等算法上分別快了1.7 倍、2.3 倍和1.3 倍.這得益于LTRU 在密鑰生成算法中使用高效混合基NTT 以及在加密和解密算法中只需要計算1 個多項式乘法.然而，Kyber 在密鑰生成算法和加密算法中均需要使用拒絕采樣生成矩陣且需要計算多項式矩陣-向量乘法，其中解封裝算法中還有重加密和重新計算多項式矩陣-向量乘法的過程，這些操作明顯更加耗時.與之對比，LTRU 方案具有運算簡單、實現高效等特點.

7 總結

基于NTRU 格的密碼系統具有結構簡潔、強安全保障、不受專利影響等優勢，有利于設計實用化高效的后量子密碼方案.本文提出了一個僅基于NTRU 單向困難性假設構造的、不使用糾錯碼也能夠壓縮密文的密鑰封裝方案LTRU.LTRU 包含一個?ND-CPA 安全的公鑰加密方案LTRU.PKE 以及一個?ND-CCA 安全的密鑰封裝方案LTRU.KEM.本文還提供了針對128 b 安全強度的參數集，及其對應的C 實現和AVX2 實現.針對LTRU 所使用的環Z2917[x]/(x648-x324+1)上的多項式乘法和除法，本文提出了一種高效的混合基NTT 算法，該算法結合單位根的性質和1-迭代Karatsuba 算法來減少乘法的數量，以提高計算效率.本文實驗結果表明，與N?ST 標準化方案Kyber-768 相比，LTRU 的公鑰尺寸降低17.9%，密文尺寸降低22.6%，帶寬降低20.2%；與N?ST 第3 輪決賽方案NTRU-HRSS 相比，LTRU 的經典安全強度和量子安全強度分別增強6 b 和5 b，以及公鑰尺寸降低14.6%，密文尺寸降低26.0%，帶寬降低20.3%，并且LTRU 的實現效率優于NTRU-HRSS.

未來工作主要包括2 點：1）對本文提出的LTRU在多平臺上實現，包括ARM Cortex-M4 實現和FPGA實現等；2）提出更多的LTRU 參數集，使其滿足更多的應用場景，如資源受限的?oT 設備和智能卡等.

作者貢獻聲明：梁志闖負責方案的設計和論文撰寫；鄭婕妤負責方案的實現；趙運磊負責論文修改.