基于GNSGA?Ⅱ算法的線圈優化設計

姜建國 佟麟閣 喻明斐

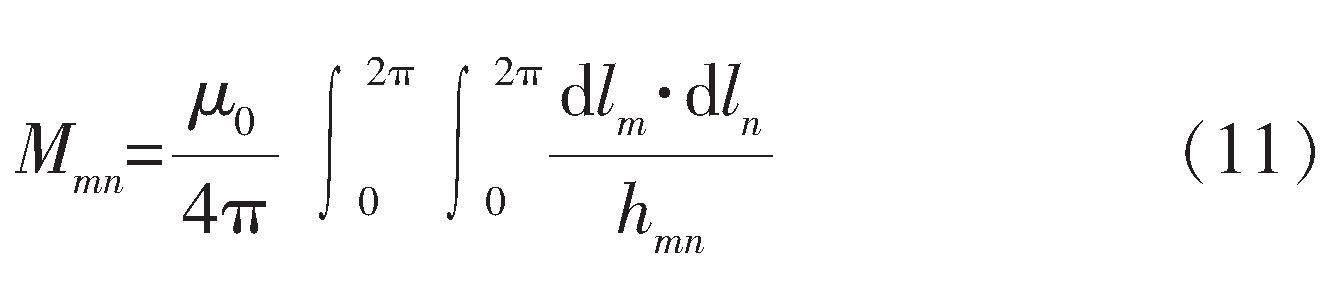
摘 要 在電動汽車無線充電技術中，充電線圈的性能直接影響系統的整體傳輸性能。在分析常用線圈形狀的基礎上，引入拉梅曲線方程，設計了一種新型超圓角方形線圈；對耦合電路進行理論分析，得到優化目標傳輸效率和功率密度與待優化參數之間的關系；利用改進的多目標優化算法（GNSGA?Ⅱ）進行線圈的參數優化，得到一組最優的參數解用于工程設計。該方法相比于傳統有限元仿真計算法，具有節省時間的優點，優化設計結果表明該方法具有有效性。

關鍵詞 多目標優化設計 GNSGA?Ⅱ算法 無線充電 超圓角方形線圈 參數優化 拉梅曲線方程

中圖分類號 TM72? ?文獻標志碼 A? ?文章編號 1000?3932（2024）01?0077?09

電動汽車有線充電形式存在充電不便、操作繁雜、復雜天氣充電不安全等問題［1～3］，而無線充電恰好可以解決此類問題，因此，研究無線充電在電動汽車領域的應用具有很高的實際價值和現實意義［4，5］。

在磁共振無線電能傳輸（Magnetic Coupling Resonant?Wireless Power Transfer，MCR?WPT）技術中，線圈是整個無線充電系統設計的核心，直接決定充電系統的傳輸性能［6，7］。合理優化線圈參數，可以保證較高的傳輸效率和較大的功率密度。在設計過程中，使用優化算法可以簡化設計步驟，加快線圈優化進程。線圈設計一般具有復雜性，可將線圈優化定義為一個多目標多參數問題，這類問題通常是通過使用多目標智能算法解決的。文獻［8］采用遺傳算法優化線圈結構，提高了線圈的耦合系數；文獻［9］將禁忌搜索算法與有限元仿真相結合，優化了耦合系數和線圈費用兩個目標；文獻［10］改進了粒子群優化算法（PSO），減少了圓形無線電能傳輸技術（Wireless Power Transfer，WPT）耦合器中的優化參數，在相同的優化性能下，該方法降低了時間成本；文獻［11］采用粒子群優化算法和有限元仿真相結合的方法，實現了傳輸效率、功率密度和線圈重量3個指標的優化設計；文獻［12］采用有限元仿真模型，通過參數掃描反復計算，實現了傳輸效率和功率密度兩個指標的優化設計。上述文獻在優化設計過程中，并未考慮線圈形狀對系統參數的影響。因此，筆者基于拉梅曲線方程設計了一種新型超圓角方形線圈，采用GNSGA?Ⅱ算法對線圈參數進行優化設計，得到了一組最優參數解。

1 線圈參數設計

1.1 線圈形狀設計

目前，在無線充電線圈上應用的線圈形狀有許多，但是大多數學者是直接選擇某一形狀后使用，未就線圈形狀對線圈參數的影響進行定量分析。

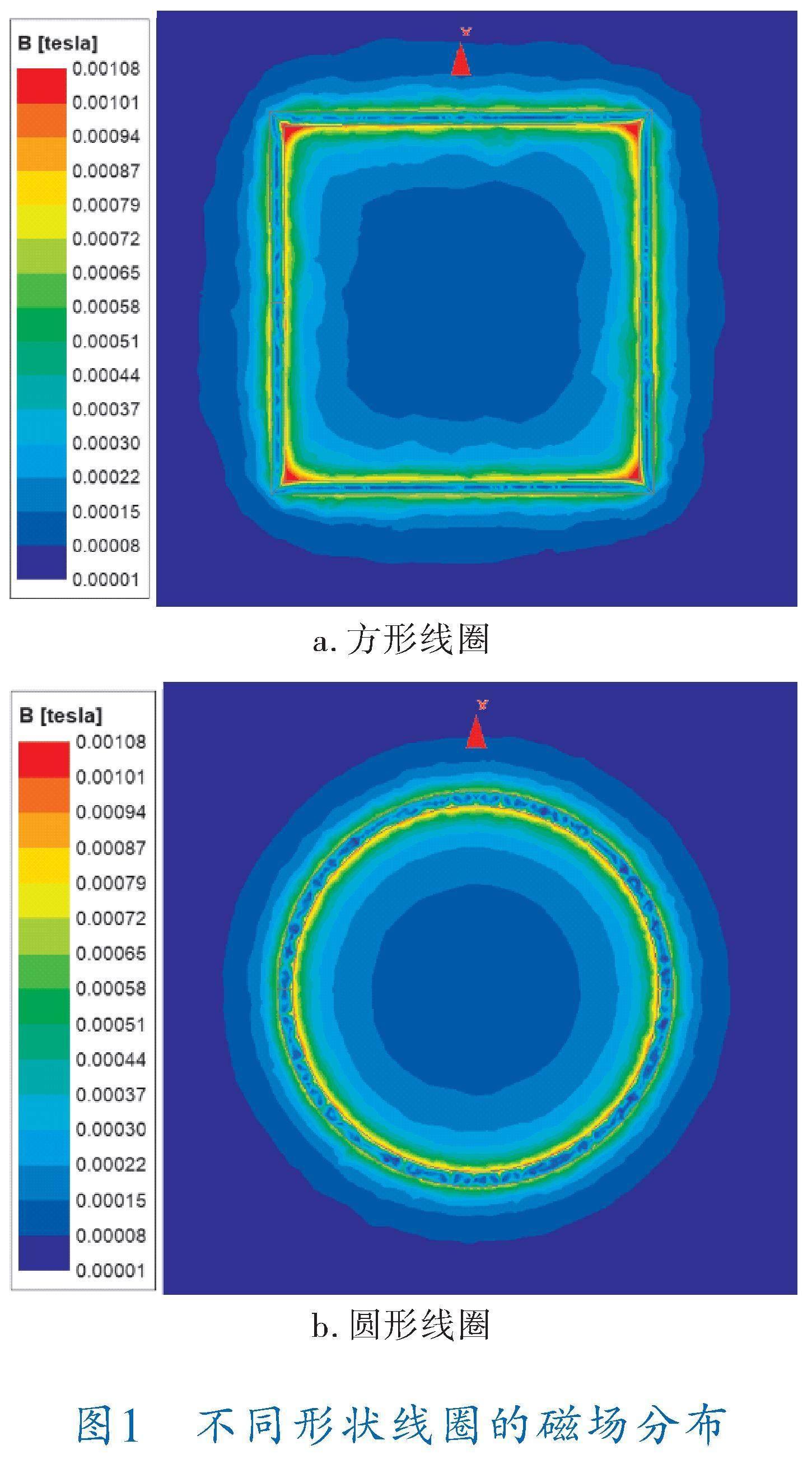
線圈的基礎形狀主要有圓形和方形，對這兩種形狀的單匝線圈模型進行特性分析，在模型中，圓形線圈直徑和方形線圈的邊長相等，均為10 cm，設置系統電流10 A、頻率85 kHz，發射線圈與接收線圈之間的耦合距離5 cm。方形線圈和圓形線圈的磁場分布如圖1所示，仿真結果見表1。從表1可以看出，圓形線圈具有良好的磁場分布，但是電感較小；方形線圈雖然具有較大的電感（電感值大意味著線圈可以承受更大的功率），但是4個角漏磁較為嚴重。因此，提出一種綜合兩者優點的線圈，通過引入拉梅曲線方程，設計出一種超圓角方形線圈。

拉梅曲線是在笛卡兒坐標系下滿足某特定方程式的點的集合，最初是由法國數學家加布里埃爾·拉梅對橢圓方程進行擴展而得，其方程式為：

其中，a、b為曲線的半直徑。

式（1）的解是一個在x∈［-a，+a］，y∈［-b，+b］的長方形內的封閉曲線，分類討論如下：

a. 當0

b. 當n=1時，曲線形狀為菱形，4個頂點為（±a，0）及（0，±b）；

c. 當1

d. 當n=2時，曲線形狀為橢圓（如果a=b則為圓形）；

e. 當n>2時，曲線形狀類似四角有圓角的長方形，曲線的曲率在（±a，0）、（0，±b）；

f. 當n=4時，曲線為方圓形；

g. 當n→∞時，曲線形狀為矩形。

本研究中，取a=b，將n>2的曲線形狀命名為超圓角方形，設定n的范圍為［2，10］，其值均取整數，其中n=2時，線圈形狀為圓形；n→∞時，線圈形狀為矩形。建立9個超圓角方形線圈模型，設置系統電流為10 A、頻率85 kHz，得到的仿真結果如圖2所示。

通過分析可知，隨著n值的不斷增大，線圈的電感是逐漸增大的，但是耦合系數是先增大后減小。同時，考慮到要盡可能減小損耗，所以取n=5時，線圈具有較高的耦合系數、較大的電感和較低的損耗，并且線圈還具有良好的磁場分布，此時該形狀的線圈最優，其磁場分布如圖3所示。

1.2 電路理論分析

磁耦合諧振式無線充電電路原理如圖4所示，主要包括發射線圈電感L、電阻R和補償電容C；接收線圈電感L、電阻R和補償電容C；I和I分別是發射線圈和接收線圈中的電流；R為系統負載；U為電源電壓；M為線圈互感。

線圈效率η的計算式為：

其中，Q、Q是兩個線圈的品質因數；ω為角速度。

由式（2）～（5）可知，線圈效率與線圈的自感、電阻和互感有關。

1.3 線圈互感的計算

兩單匝同軸線圈間的互感如圖5所示。首先求解發射線圈中由外向內的第m匝線圈以及接收線圈中由外向內的第n匝線圈之間的互感，其半直徑分別記為a和a，分別以兩線圈中心為原點建立坐標系［13］，如圖5所示。其中，線圈m、n中的微元分別記作dl、dl；γ、δ分別為微元dl和dl與x軸的夾角；h為兩線圈之間的垂直距離；h表示微元dl和dl之間的距離；d為線徑；p為發射線圈匝間距；r和r分別為發射線圈和接收線圈的外半徑。

由圖5可得：

兩單匝線圈的半直徑可分別表示為：

a=r-（m-1）（d+p）（9）

a=r-（n-1）（d+p）（10）

其中，p為接收線圈匝間距。

由諾依曼公式可知，兩同軸單匝線圈間的互感M可表示為：

其中，μ為真空或空氣磁導率，取4π×10-7 H/m。

同軸平面線圈間的互感M可以看作是兩線圈內部各單匝線圈互感之和：

1.4 線圈自感的計算

線圈自感可以近似看成是其內部每匝線圈的自感以及內部任意兩匝線圈之間的互感之和［14］。其中，兩匝線圈間的自感示意圖如圖6所示。

則線圈自感表達式為：

其中，N、N、N∈N；k′為線圈匝數。

1.5 線圈電阻的計算

線圈導線一般采用銅導線或者多股利茲線。多股利茲線是由多股漆包線絞合在一起的導線，減小了集膚效應帶來的損耗，而且可以基本消除各相鄰導線的臨近效應。相比于銅導線，利茲線優勢較為明顯，因此一般選用多股利茲線作為電動汽車無線充電線圈的導線。

本研究中，使用800股線徑為4 mm的利茲線，其交流電阻R估計計算式為：

其中，K為絞合系數，這里取1.03；ρ為電導率，其值為1.72×10-8 S/m；l為線圈的總繞線長度；N為股數；d為單股線的線徑；系統的工作頻率f為85 kHz。

線圈的總繞線長度l的計算式為：

其中，a為第k′匝線圈的半直徑，r為線圈外半徑，w為線圈匝間距。

2 線圈參數多目標設計方法

無線充電線圈的優化設計是一個多目標多參數優化問題。在磁耦合器中，線圈是電動汽車無線充電系統能量傳輸的基本載體，線圈的形狀、結構和尺寸直接影響磁耦合器的電氣參數，如自感、互感及耦合系數等，同時也會影響磁耦合器的磁場分布特性和空間偏移特性。因此，在設計磁耦合器時需要對線圈進行充分的結構分析和優化，以實現最佳的性能。

相比于傳統的試湊法，采用優化算法進行線圈參數優化設計可以節省大量的時間成本。因此，需要建立準確的目標函數方程，使用優化算法得到更為精確的解。本研究通過改進NSGA?Ⅱ算法來提高優化參數解解集的質量。

在無線充電系統中，功率密度和傳輸效率是系統評價性能是否良好的兩個重要參數，傳輸效率越高，系統損耗則越小，這樣無線充電系統的經濟性更好，因此將系統傳輸效率作為一個目標函數。由于接收線圈安裝在電動車底部，受到汽車自重和內部空間大小的限制，接收線圈需設計得精致小巧，以節省空間，又不影響功率傳輸。因此將無線充電線圈的功率密度作為第2個目標函數。

2.1 優化目標函數

建立以無線充電線圈的傳輸效率和功率密度為優化目標的目標函數。

2.1.1 傳輸效率

通過之前的理論分析可知，系統傳輸效率與線圈耦合系數k以及線圈的品質因數Q有關，其目標函數為：

2.1.2 功率密度

在設計中，提高線圈的單位面積傳輸功率可以減小接收線圈的重量和體積，這對電動汽車而言，可以節省更多的空間來安裝電池組或其他設備。將λ定義為接收線圈單位面積的傳輸功率，其計算式為：

其中，P為系統設計額定功率；S為接收線圈的面積。

2.2 約束條件

在設計優化線圈過程中，需要考慮其他因素對線圈的約束。首先考慮線圈的安裝環境，其線圈半直經不能超過車自身的寬度，而且線圈的匝間距應該大于導線材料的直徑，其中導線線徑d為4 mm。設發射線圈的外半徑為r，匝數為N，匝間距為w；接收線圈的外半徑為r，匝數為N，匝間距為w，參數取值見表2。

2.3 優化模型

結合以上分析，本研究的優化問題可以表示為：在滿足基本線圈尺寸的前提下，以傳輸效率最高、功率密度最大為目標，確定發射線圈和接收線圈的尺寸、匝數和匝間距；設定傳輸效率的倒數和功率密度的倒數為目標函數，則線圈多目標優化的模型如下：

在上述目標優化問題中，優化參數為6個變量的集合，目的是為了尋找一組使所有目標盡可能達到最優的解，這個解稱為Pareto最優解，所有的Pareto前沿構成Pareto最優解集。

3 基于GNSGA?Ⅱ算法的磁耦合機構優化設計

求解多目標優化問題過程中，目標函數之間往往是互相矛盾的，因此需要計算出滿足這些目標函數的相對最優的Pareto解集。

一般多目標優化算法有MOGA、NSGA、SPEA等。與NSGA算法相比，NSGA?Ⅱ算法通過采用精英保留策略擴大了采樣空間，防止優良個體丟失，保證了種群的多樣性，提高了算法的運算速度和魯棒性，使最優解能夠分布在Pareto前沿。然而該算法依然存在缺陷，NSGA?Ⅱ算法所提出的個體擁擠距離計算方式存在局限性，從而導致種群的分布不均勻。

3.1 NSGA?Ⅱ的擁擠機制缺陷

NSGA?Ⅱ算法通過計算個體擁擠距離建立擁擠度排擠機制。在每次迭代時，通過分層排序計算出種群個體之間的距離，在同一層級中，將擁擠距離大的種群個體篩選出來，繼續進行下一次迭代。因此，該機制存在以下缺陷：

a. 無法從整個種群分布的角度看待個體周圍的密集程度；

b. 基于擁擠距離的排擠機制無法準確測量同一層級中相鄰個體的密集程度。

由此可知，NSGA?Ⅱ算法無法準確計算個體的密集程度，導致最優解集分布不均勻，而且也會出現解集的“中斷”。

3.2 GNSGA?Ⅱ算法個體鄰域的構建

基于對NSGA?Ⅱ算法缺點的分析，引入DBSCAN算法中的鄰域思想［15］改進NSGA?Ⅱ算法的擁擠機制，形成GNSGA?Ⅱ算法。DBSCAN算法是一種基于密度的聚類算法，其核心思想是用一個點的鄰域內個體數量來衡量個體周圍的密集程度，此點密度半徑以內所有點的集合稱為該點在此密度半徑下的鄰域。

設x∈X，稱N（x）={y∈X：d（y，x），θ}為x的θ鄰域，顯然，x∈N（x）。

目標函數的種群密度半徑計算式為：

其中，F和F表示種群在目標函數下F（x）的最大值與最小值；m為種群大小。因此，θ就可以表示為在目標函數F（x）下兩個個體間的平均距離，這就可以保證種群個體的均勻分布。

GNSGA?Ⅱ算法的流程如圖7所示。

3.3 GNSGA?Ⅱ算法的測試與分析

通過選取兩個兩目標測試函數ZDT1、ZDT2和一個三目標函數DTLZ7對GNSGA?Ⅱ算法進行測試，算法參數設置為：種群規模100，進化代數500，交叉概率0.9，變異概率0.1。測試結果如圖8～10所示，可以看出，相比于NSGA?Ⅱ算法，GNSGA?Ⅱ算法的Pareto前沿具有更好的分布性。

4 線圈優化結果分析

接下來使用GNSGA?Ⅱ算法對磁耦合線圈參數進行求解，在其目標函數的約束條件內，尋找最佳匹配的磁耦合線圈參數，使MCR?WPT系統的傳輸效率和功率密度相對最優。設置GNSGA?Ⅱ算法的交叉概率為0.8、變異概率為0.1、種群大小為200、迭代次數為200。仿真得出的Pareto曲線如圖11所示，可以看出，Pareto前沿逐漸降低，前沿分布平滑均勻，并未陷入局部最優。

效率與功率密度的關系如圖12所示，可以看出，系統的輸出效率和功率密度之間呈負相關，在耦合線圈不同的匹配參數下，隨著傳輸效率的提升，功率密度會減小。

測試的部分前沿解列于表3，可以看出，發射線圈變化較小，隨著接收線圈尺寸的減小和匝數的減少，傳輸效率逐漸減小，功率密度逐漸增加。

在實際工程中，需要根據設計者需求選擇一組最優設計值。對于參數解集，使用加權歸一化處理，得到最優解。此處傳輸效率的權重選擇0.8，功率密度的權重選擇0.2，其加權歸一化公式為：

其中，F為參數解集中的第i個解；F（n）和F（n）為第n個目標的最小值和最大值；G為目標權重；n為待優化目標個數。

根據上述分析得出1組最優解，詳見表4。

5 結束語

以電動汽車無線充電系統的磁耦合線圈為研究目標，進行優化設計。首先引入拉梅曲線方程設計新型超圓角方形線圈，該線圈具有良好的磁場分布和較優的性能；接著建立無線充電系統的電路模型，對影響優化目標性能的3個電氣變量參數（線圈自感、線圈互感和線圈電阻）進行理論分析；然后以系統傳輸效率和功率密度為優化目標，以發射線圈和接收線圈的外半徑、匝數和匝間距的取值范圍作為約束條件，建立無線充電線圈多目標優化數學模型。最后，使用GNSGA?Ⅱ優化算法對線圈進行優化設計，在目標函數的約束條件下，得到了Pareto最優解集。根據設計者使用的實際情況，對解集進行了加權歸一化處理，得到了一組最優設計值，可為工程設計提供參考。

參 考 文 獻

［1］ 李陽，石少博，劉雪莉，等.磁場耦合式無線電能傳輸耦合機構綜述［J］.電工技術學報，2021，36（S2）：389-403.

［2］ 廖力，劉坤，吳鐵洲.電動汽車無線充電系統阻抗補償方法研究［J］.電源技術，2021，45（3）：374-377.

［3］ 馬精慧，宋楊.基于線性變參數模型的汽車移動無線充電系統研究［J］.電子測量技術，2018，41（4）：16-23.

［4］ 崔淑梅，宋貝貝，王志遠.電動汽車動態無線供電磁耦合機構研究綜述［J］.電工技術學報，2022，37（3）：537-554.

［5］ 劉寶航，王秉森，李子奇.磁耦合諧振式無線電能發射系統的設計與實現［J］.電子測量技術，2019，42（10）：28-32.

［6］ 吳理豪，張波.電動汽車靜態無線充電技術研究綜述（上篇）［J］.電工技術學報，2020，35（6）：1153-1165.

［7］ 吳理豪，張波.電動汽車靜態無線充電技術研究綜述（下篇）［J］.電工技術學報，2020，35（8）：1662-1678.

［8］ WANG S C，XU C，WEI B，et al.Analysis and optimization of coil structure of magnetic circuit mechanism for electric vehicle wireless charging system［J］.IOP Conference Series：Earth and Environmental Science，2021，675（1）：012098.

［9］?? HASSAN M A，HAILAT N，BADAWI N，et al.A wireless power transfer system with optimized circuit parameters using genetic algorithm［J］.International Renewable Energy Congress，2017：386-389.

［10］?? BOSSHARD R，KOLAR J W，MUHLETHALER J，et al.Modelingand α?η?pareto optimization of inductive power transfer coils for electric vehicles［J］IEEE Jounal of Emerging and Selected Topics in Power Electronics，2015（1）：50-64.

［11］?? YILMAZ T，HASAN N，ZANE R，et al.Multi?objective optimization of circular magnetic couplers for wireless power transfer applications［J］.IEEE Transactions on Magnetics，2017，53（8）：1-12.

［12］?? BANDYOPADHYAY S，PRASANTH V，BAUER P，et al.Multi?objective optimization of a 1 kW wireless IPT system for charging of electric vehicles［C］//2016 IEEE Transportation Electrification Conference and Expo.Dearborn，MI，USA：ITEC，2016：1-7.

［13］ 吳昕，何小斌，藍建宇，等.基于螺線方程的MCR?WPT系統線圈設計［J］.電源學報，2021，19（5）：75-82.

［14］ 陳忠華，盧韋，時光，等.無線電能傳輸系統的線圈參數及耦合系數研究［J］.高壓電器，2019，55（4）：205-210.

［15］ 王光，林國宇.改進的自適應參數DBSCAN聚類算法［J］.計算機工程與應用，2020，56（14）：45-51.