融合加窗和自適應加權引導濾波改進的Canny算法

郝霜 李金鳳 翟迅步

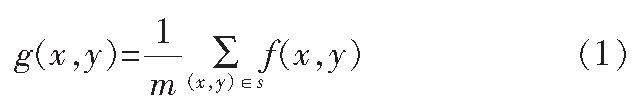
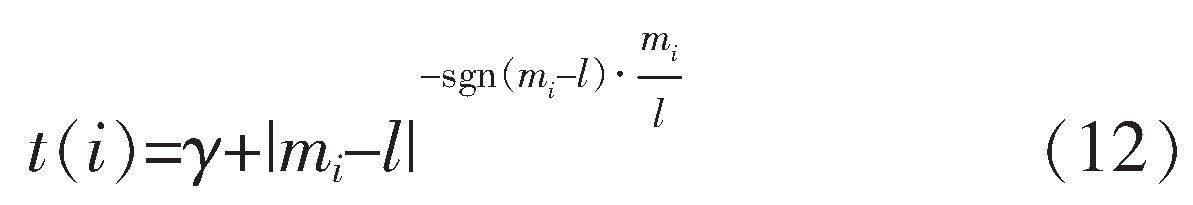
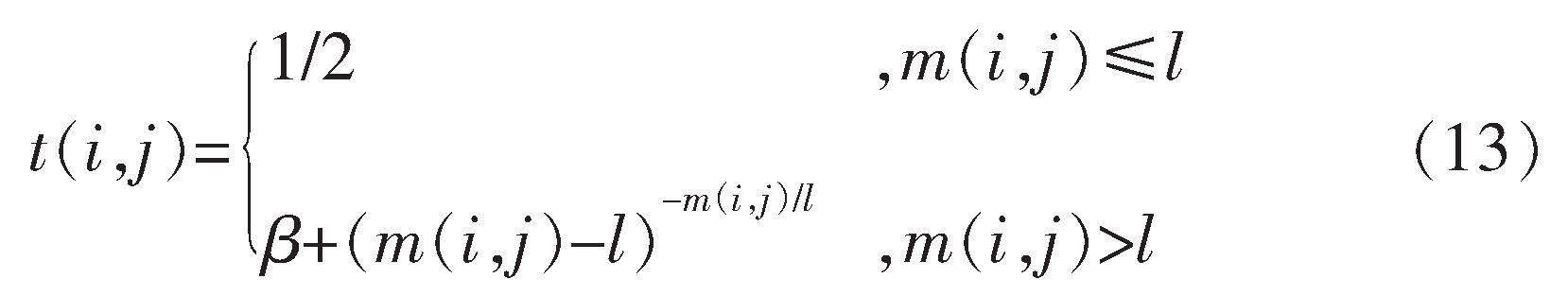
摘 要 針對Canny算法濾波過程中圖像細節部分缺失和無法有效去除噪聲，并且無法動態識別圖像邊緣的問題，提出一種融合加窗和自適應加權引導濾波的Canny算法。該算法對Canny算法做出兩點改進：一是使用加窗濾波器對圖像進行處理，有效濾除噪聲，然后對圖像進行數學形態學濾波處理，有效增強圖像邊緣；二是引入分段權值模型對引導濾波算法的正則化參數自適應修正，使其能夠根據梯度信息區分邊緣和非邊緣，從而達到動態識別圖像邊緣的效果。相比傳統Canny算法，改進算法處理后的信噪比提高了1.05～5.22 dB，品質因數提高了0.16～0.35。實驗結果表明：改進算法能有效濾除椒鹽噪聲，識別出比較清晰和完整的邊緣。

關鍵詞 Canny算法 邊緣檢測 加窗濾波器 數學形態學 自適應加權引導濾波

中圖分類號 TP14? ?文獻標志碼 A? ?文章編號 1000?3932（2024）01?0086?06

圖像的邊緣檢測是信息處理過程中尤其重要的一個步驟。邊緣檢測［1］是選擇使用某種算法來提取圖像中目標和背景灰度值變化最大的交界線。Canny算法可以非常準確地找到圖像中盡可能多的邊緣，很大程度上能避免圖像邊緣的遺漏和檢測到錯誤圖像的邊緣。目前，由于Canny算法有著信噪比比較大、檢測邊緣的準確度高以及數據計算量比較小的優點，因此廣泛應用于圖像邊緣檢測中。Canny算法雖然是一種多級邊緣檢測［1］算法，但處理的方法和過程相對簡單，算法的計算難度系數比較低。其在圖像邊緣檢測中存在著一定的缺點，主要有以下原因：

a. 在圖像平滑處理過程中選擇的是二維高斯濾波，由于選擇高斯標準差σ的隨機性，結果就是圖像平滑效果不能達到理想的選擇，對圖像噪聲去除不足；

b. 在計算梯度強度和方向過程中，選擇使用水平、垂直和對角邊緣的4個算子，由于算子的方向比較少，這就容易導致圖像邊緣的細節缺失，且無法根據梯度動態識別邊緣和非邊緣的區別。

文獻［2］針對圖像邊緣模糊和邊緣不連續的問題，提出了一種改進數學形態學的方法。但是，該算法僅對齒輪這種相對比較簡單的圖像邊緣檢測作用比較好。文獻［3］在遙感圖像邊緣檢測的過程中提出加窗均值濾波方法，減少采集過程中隨機噪聲對圖像的影響，增加算法對邊緣檢測的準確性。但是，該算法檢測的圖像邊緣存在部分細節缺失的情況，只合適于邊緣比較簡單的道路類圖像的邊緣檢測。文獻［4］在圖像分割中利用引導濾波的保邊特性充分保留圖像邊緣。但是，該算法對噪聲敏感，穩定性不好。文獻［5］針對提取圖像的微弱邊緣困難的問題，提出了一種改進MSR的方法，該方法不僅能減少噪聲對微弱邊緣的影響，還能更好地恢復圖像的本質。但是，其在檢測比較復雜的圖像邊緣過程中容易出現邊緣冗雜的問題，并且自適應效果的效果比較差。文獻［6］提出采用改進后的Canny算法和多尺度形態學對圖像進行處理，將兩個結果融合得到最后的圖像邊緣。文獻［7］提出在FPGA實現過程中，再引入一個對數單位，將除法變為減法，算法在節省資源的同時不影響閾值。

筆者提出了一種改進的Canny算子邊緣檢測算法。首先通過加窗濾波器對圖像進行處理，有效地消除圖像采集過程中產生的噪聲，增強圖像對隨機噪聲的抗干擾能力，然后利用數學形態的算法對濾波后的圖像進行邊緣增強，再引入分段權值模型對引導濾波算法的正則化參數自適應修正，提升自適應判別邊緣的能力，使得圖像具有很強的魯棒性。

1 傳統Canny算法

傳統Canny檢測邊緣的步驟如下［8］：

a. 圖像去噪，利用高斯濾波器對圖像進行平滑處理；

b. 計算圖像梯度，得到可能的邊緣；

c. 對幅值進行非極大值抑制；

d. 雙域值篩選。

2 改進后的Canny算法

2.1 改進后的加窗濾波算法

均值濾波可以歸于線性濾波其中的一種類型，其算法選用的方法為鄰域均值法［3］。均值濾波實質是對圖像的每一個像素點周邊的像素點進行加權求平均值的計算，然后將計算結果賦值給這個點：

其中，g（x，y）為經過均值濾波后的圖像；f（x，y）為原始圖像；m為模板s內所有點的數量總和。

在中值濾波算法與鄰域均值濾波算法［3］的基礎上，筆者提出使用變化的模板（窗口）進行濾波，能更加細致地處理圖像去除噪聲，進行有針對性地濾波，增加圖像采集過程中產生隨機噪聲時對邊緣信息的保護能力。首先對模板內的灰度值進行排序，以中間部分的像數點的數值作為模板中心像素：

其中，G（x，y）為處理后圖像；s為模板內不同像素點排序后完成后，其中間部分像素點的集合；m為模板s內所有像素點的總個數。

如果m的值等于1，G（x，y）是中值濾波算法；如果m的最大值為m，最小值為1，G（x，y）是鄰域均值濾波算法。由以上可以看出通過不同的中間窗體的尺寸變化，筆者可將中值濾波算法和鄰域均值濾波算法相融合，既能增強Canny算法抗噪聲的干擾能力，又能降低圖像的不連續性，能夠很好地抑制假邊緣，檢測邊緣的準確性比較高。

2.2 數學形態學運算

數學形態學處理算法是以數學形態學［2］作為處理圖像的方法，數學形態學運算的實質是一種非線性運算，其中主要有膨脹、腐蝕、開運算和閉運算，這些基本算法對于二值圖像和灰度圖像有不同的作用。

膨脹運算。用3×3的圖像矩陣B與二值圖像A進行“與”運算，其作用是使得圖像的邊緣變粗：

C=A☉B（3）

腐蝕運算。用3×3的圖像矩陣B與二值圖像A進行“或”運算，其作用是使圖像的邊緣變細：

開運算［9］。將圖像先腐蝕后膨脹定義為開運算，其作用是在去除噪聲的同時，平滑較大的物體邊界，對圖像的邊界得到了一定程度的補償，簡單來說，就是清除邊緣的噪點：

閉運算［9］，將圖像先膨脹后腐蝕定義為閉運算，其作用是將物體內部的細小空洞填充起來，與接近的物體連接起來，簡單來說，就是清除內部空洞：

2.3 改進后的數學形態學運算

對上面提到的問題，筆者提出一個改進算法：

其中，B是3×3的矩陣，B是5×5的矩陣，具體定義如下：

因為B和B有著不同的尺度結構，所以B和B具備不同的去噪能力。較小的尺度對圖像細節的保護較好，但容易檢測出虛假邊緣，去噪能力較弱；大尺度的結構元素反而具有較強的去噪能力，只是在圖像細節的保護上稍顯遜色，邊緣信息也容易丟失。因此，筆者采用復合形式濾波器，在有效過濾噪聲的同時，避免了單一結構元素的弊端。在保護圖像細節信息的情況下，能夠增強圖像的微弱邊緣。

2.4 自適應加權引導濾波邊緣檢測算法

引導濾波算法利用引導圖像［4］與濾波輸出圖

像［4］之間的局部線性關系，引導濾波器的引導圖像I和濾波器輸出Q之間的局部線性關系的模型為：

Q=aI+b，?i∈ω（8）

其中，（a，b）是窗口ω中的常數。

通過式（8）計算線性函數相關系數，在窗口中使以下代價函數最小：

其中，是一個正則化參數；p為濾波器輸入。為了避免a過大，需要對濾波器的平滑度進行控制。式（9）的解為：

對式（9）中的正則化參數進行改進，并引入了隨梯度信息變化的自適應權值向量t，將原有的參數替換為/t。該改進不僅具有原始的平滑作用，還能夠根據梯度信息識別出邊緣和非邊緣，并自適應地控制平滑效果；同時，還引入分段權值模型，對平滑參數進行了自適應修正：

其中，γ為常數項，防止分母項為零；m為圖像梯度；l為梯度閾值。

在進行大量的仿真實驗后，放棄了原來對非邊緣區域的權值處理方法，并采用了一個固定的常數值1/2。該值被放置在改進后的平滑參數的分母處，從而對于非邊緣區域而言，平滑效果會提高原來的兩倍，改進后的權值模型為：

通常情況下，式（13）中β值為4。在引入權值模型后，式（10）改寫為：

此時，結合2.1和2.2節的操作，筆者提出的算法的輸出函數為：

實現兩種算法與自適應加權引導濾波邊緣檢測算法相結合的操作流程如圖1所示。

邊緣檢測算法相結合的操作流程

3 仿真結果與分析

3.1 仿真結果

為了驗證筆者所提算法對圖像處理的有效性，分別用筆者算法、Canny算法及文獻［3］算法對相同的圖像進行處理，結果如圖2所示。

在圖像采集過程中容易產生隨機噪聲，而噪聲對圖像檢測邊緣有比較大的干擾。在實驗過程加入椒鹽噪聲來驗證算法對噪聲的圖像邊緣檢測的影響。圖2a、b分別是原始圖像、加入椒鹽噪聲后的圖像，圖2c、d是傳統Canny算法分別對原圖和加噪聲圖像處理后得到的圖像，圖2e、f是筆者所提算法分別對原圖和加噪聲圖像處理后得到的圖像，圖2g、h是文獻［3］分別對原圖和加噪聲圖像處理后得到的圖像。由圖2可以直觀地發現，筆者提出算法對圖像的處理效果最好，細節部分的邊緣檢測更加細致，在加入椒鹽噪聲后，對邊緣檢測的結果影響比較小，檢測到的邊緣準確性比較高，保留了更多的細節。

3.2 性能分析

測試邊緣檢測算法的性能，不僅能通過邊緣檢測的直觀結果來評價邊緣檢測的性能，而且還能通過信噪比（Signal Noise Ratio，SNR）和品質因數（FM）來評價邊緣檢測的性能。

信噪比［10］定義如下：

其中，M、N分別為圖像長度和寬度上的像素個數，g（i，j）、f（i，j）分別為原始圖像和去噪后圖像在點（i，j）處的灰度值。SNR的數值越大，表明圖像的質量越好，邊緣檢測算法的性能越好。

品質因數［11］的定義：

其中，NA、NL分別為檢測到的邊緣和理想邊緣；?為錯位邊緣的補償系數；d為實際檢測到的邊緣和圖像的理想邊緣之間的距離。FM越大，表明理想邊緣與實際邊緣越接近，邊緣檢測算法的性能越好。

分別運用筆者算法、傳統Canny算法、文獻［3］算法和文獻［4］算法在無噪聲環境下和椒鹽噪聲環境下的圖像進行對比實驗，采用SNR和FM評價本算法的濾波效果和邊緣識別的準確性。從圖像數據集中選取4幅（分別為自行車、螺母、X光、手勢）照片，原圖大小為256×256，如圖3所示。

不同算法對圖3圖片處理后的SNR和FM值見表1。

根據實驗圖庫，自行車、螺母的圖像屬于紋理比較復雜并且邊緣比較多的圖像；X光的圖像和手勢圖像都是紋理比較簡單并且邊緣比較少的圖像；筆者算法的SNR和FM值都高于對比算法，由表1的結果可知筆者算法對圖像的邊緣檢測有著比較明顯的效果。

終上所述，在椒鹽噪聲環境下筆者算法的SNR和FM都有一定程度的增大，筆者所提出的算法效果相比于其他算法較好，有著很好的濾除椒鹽噪聲的效果，可以有效地保護邊緣的信息，能夠檢測到細節部分的邊緣。

4 結束語

細致地分析了傳統Canny算法的優缺點，并且提出了改進缺點的方法和步驟，使得改進后的Canny算法具有比較強的魯棒性。針對Canny算法濾波過程中圖像細節部分缺失和無法有效去除噪聲，并且無法動態識別圖像邊緣的問題，提出一種融合加窗和自適應加權引導濾波的Canny算法。該算法能有效地去除椒鹽噪聲并且增加算法對隨機噪聲的抗干擾能力，然后通過自適應加權引導濾波算法能夠隨梯度信息自適應調整平滑力度，檢測出更多的邊緣細節，增強圖像邊緣層次感。表明采用筆者提出的算法圖像的SNR值和FM值均高于對比算法。

參 考 文 獻

［1］ 胡佳林，劉波峰，何玉成.基于遺傳算法的Canny邊緣檢測算子在配藥機器人中的應用［J］.傳感器與微系統，2013，32（7）：141-143；147.

［2］ 杜偉，何毅斌，吳林慧，等.融合改進形態學和LOG算子的齒輪邊緣檢測［J］.武漢工程大學學報，2021，43（6）：675-680.

［3］ 馬為駽，張龔，馬傳香，等.不同光照條件下含噪遙感圖像邊緣檢測算法［J］.吉林大學學報（工學版），2023，53（1）：241-247.

［4］ 劉麗霞，李寶文，王陽萍，等.改進Canny邊緣檢測的遙感影像分割［J］.計算機工程與應用，2019，55（12）：54-58；180.

［5］ 包從望，胡才夢，張彩紅，等.基于改進Canny算子的齒輪缺陷檢測邊緣檢測算法［J］.組合機床與自動化加工技術，2023（1）：83-86；91.

［6］ 唐守鋒，翟少奇，仝光明，等.改進Canny算子與形態學融合的邊緣檢測［J］.計算機工程與設計，2023，44（1）：224-231.

［7］ GUO L G，WU S T.FPGA Implementation of a Real?Time Edge Detection System Based on an Improved Canny Algorithm［J］.Applied Sciences，2023，13（2）：870.

［8］ 孔珊珊，降愛蓮.基于第二代模糊集閾值選擇的圖像Canny邊緣檢測［J］.計算機應用與軟件，2013，30（12）：160-162；307.

［9］ YU X K，WANG Z W，WANG Y H，et al.Edge Detection of Agricultural Products Based on Morphologically Improved Canny Algorithm［J］.Mathematical Problems in Engineering，2021（3）：1-10.

［10］ 沈衛東，李文韜，劉娟，等.基于改進Canny邊緣檢測的指針式儀表自動讀數算法研究［J］.國外電子測量技術，2021，40（2）：60-66.

［11］ 韓軍，張鴻宇.迭代式自適應法在Canny算子中的應用與研究［J］.機械設計與制造，2019（12）：15-18.