基于改進ALNS 算法的離散制造車間物料配送路徑優化研究

何家錚，王家海

（同濟大學 機械與能源工程學院，上海 201804）

0 引言

在離散制造領域，為了滿足個性化和快速響應市場的需求，多品種、小批量的生產模式變得越來越普遍。這種生產模式的靈活性雖然能夠滿足市場多變的需求，但同時也大幅增加了車間內物料配送的難度和復雜性。物料配送的效率和準確性直接影響到整個生產流程的順暢和成本控制[1]，如何在保證物料按時供應的同時，減少配送時間和成本，如何優化配送路徑以適應車間內復雜多變的布局和需求，都是亟待解決的問題。

在這樣的背景下，研究和開發高效的物料配送路徑優化算法變得尤為重要。車輛路徑規劃問題（VRP）被學者廣泛研究，例如唐等[2]利用蟻群算法求解，也有部分學者探索了柔性制造車間的物料配送問題[3]，但通常未能精確結合車間實際情況，采用歐式距離作為節點距離，本文考慮車間通道約束、時間窗、小車容量、線邊庫容量等因素，通過引入和改進自適應大領域搜索（ALNS）算法解決求解離散制造車間物料配送的路徑優化問題。

1 數學模型建立

1.1 問題描述

一個離散型制造車間，車間內有一個中心倉庫和N 個物料需求工位點，由配送能力為Q 的AGV 執行物料配送作業，每個由物料需求的工位對物料存在時間窗要求[ETi，LTi]，找到最佳的運輸車輛數以及最佳的運輸路線。

基本假設如下：

（1）車輛從車間倉庫裝貨后出發，經過各車間工位后最終返回車間倉庫。

（2）單個工位的物料需求量不超過AGV 的運輸載荷。

（3）一次配送任務中，單個工位的物料由同一輛AGV 小車完成配送，若配送完畢后有新的物料需求，增加新的配送任務由其他AGV 進行配送。

（5）物料需求點時間窗為軟時間窗，且AGV 允許部分超載。

1.2 符號說明

在詳細闡述具體的模型建立和求解過程之前，對模型中涉及的關鍵符號及變量進行詳細定義，以確保理論推導的嚴密性和結果解讀的一致性，相關符號變量見表1。

表1 數學模型符號說明

1.3 工位物料時間窗模型

針對晚于LTi到達的情況，該工位生產停滯，長時間后會影響相應工序的其他工位生產，對生產系統整體影響較大。針對早于ETi到達的情況，AGV 送抵的物料會超出線邊庫的最大庫存，因此需等待線邊庫有足夠庫位后進行服務。即當ATi＜LTi時，令ATi=ETi，同時由于等待會產生等待懲罰。

1.4 車間通道約束下的距離模型

如圖1 左所示，在傳統車輛路徑問題（VRP）中，節點間距離通常通過歐氏距離計算。適用于直線可達的場景。在車間環境中，由于路線限制和復雜布局，工位間不能直接以直線方式行駛，必須沿固定路徑，如圖1 右所示。采用像Floyd 算法這樣的圖論方法來計算最短路徑以及尋找其路由[4]，比直線距離更能反映車間內的實際行駛條件，為車間VRP 問題提供更準確的解決方案。

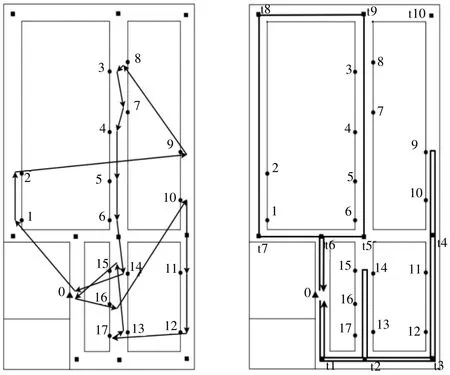
圖1 傳統VRP 路徑與車間通道約束下的路徑圖

1.5 物料配送成本模型

式（4）是以配送成本最小為目標函數，包括路徑成本、超載懲罰和時間窗懲罰，每輛小車r成本的具體計算方式為：遍歷小車（路徑）r下的k個路徑節點，計算節點k至節點k+1 的路徑距離并累加，計算該路徑下k個節點的需求量之和小車載重之差并附加超載懲罰系數，以及通過式（3）計算時間窗懲罰；式（5）確保配送順序合理，同一條線路中當前節點小車的到達時間需大于等于上一個節點的到達時間、上一個節點的服務時間、兩點之間移動時間之和；式（6）表示除了倉庫節點0和i的集合完全相等，即每個工位一次只能由一輛配送小車配送，且只能被一輛AGV 配送一次；式（7）表示每輛AGV 的起點和終點都是車間倉庫。

再者，這里是具有造船傳統的女真人聚居區。遠的不說，女真人的先世挹婁人就能造船，元代的女真人已能建造遠征日本的大型戰船。選擇在這里造“巨舡”，不缺人才和技術，能夠迅速完成造船任務。據此，明廷把船廠設在今吉林市阿什哈達村。

2 模型求解

基于車間布局、工位和拐點的位置，建立初始距離矩陣，并利用Floyd 算法求解通道約束下的最短距離矩陣，并基于此矩陣利用改進的ALNS 方法進行車間物料配送路徑規劃問題的求解，如圖2 所示。

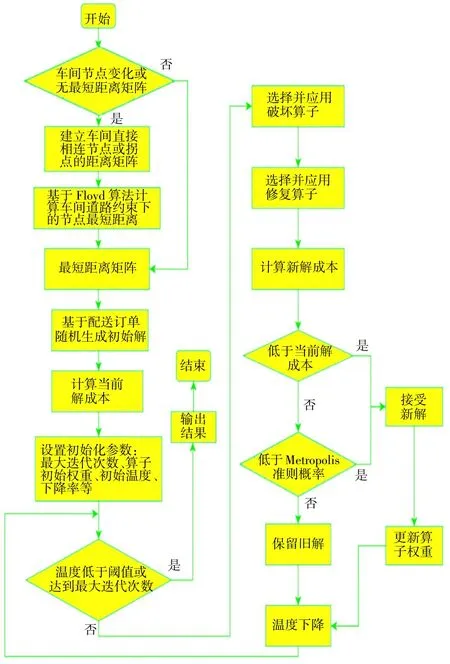
圖2 模型求解流程圖

2.1 Floyd 算法預處理

初始化，根據車間布局，基于圖論，將同一通道上相鄰的工位節點或車間拐點認定為“聯通”，并設置最短距離為實際直線距離，對于不同通道上的節點，需要經過車間通道拐點到達，因此距離初始為無窮大，得到一個包含車間拐點的（N+t）×（N+t）初始距離矩陣A0。

迭代更新，對于不直接連通的節點對，利用式（8）找到通過一個或多個中間節點的最短路徑，從而更新這些節點對之間的最短距離，每次迭代更新距離矩陣Ant。

當迭代次數nt=N+t時，迭代終止，移除車間拐點即得到N×N的基于車間路徑約束的實際節點距離矩陣A′。Floyd 算法的時間復雜度是O（n3），空間復雜度是O（n2），其中，節點距離矩陣A′是后續物料配送的必要環節，其僅需要在車間布局變化時重新運算，否則只需運算一次。

2.2 ALNS 算法求解車間物料配送的VRPTW 問題

自適應大領域搜索算法（ALNS），是一種用于求解復雜優化問題的啟發式算法[5]。它通過不斷地摧毀和修復當前解的一部分來探索解空間，可以根據歷史表現適應性的調整摧毀和修復的使用頻率。

改進的ALNS 算法采用外層模擬退火，內層ALNS 的方式減少陷入局部最優的概率。ALNS 的每次迭代后進行成本比較，若新解是最優解則接受，否則以采用Metropolis 準則的方式接受相對劣解。

2.2.1 生成初始解

初始解編碼示例如圖3 所示。打亂節點數組I，依次分配給小車，當∑Di＞Q時，新增一輛小車，直至所有節點分配完畢。

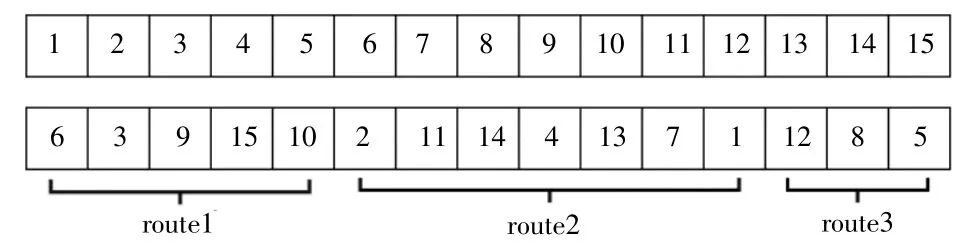
圖3 初始解編碼示例

2.2.2 破壞和修復算子

本研究共采用3 個破壞算子和3 個修復算子，根據算子權重選擇破壞算子和修復算子。如圖4 所示，第一步：破壞，遍歷當前解中的所有路徑的節點，依據不同破壞規則從節點數組中選取一定數量的節點進行破壞移除，并加入移除節點列表；第二步：修復，根據不同的修復規則，將移除節點列表中插入被破壞的節點列表中。

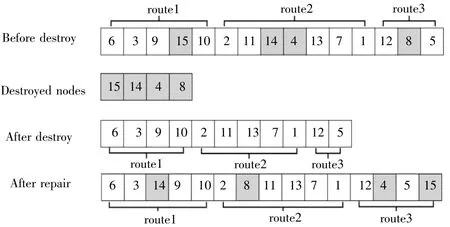
圖4 破壞和修復

（1）相關性破壞算子，也稱Shaw 移除算子，目的是通過破壞相似或相關的節點來探索解空間的不同區域，本文基于節點的距離、時間窗和物料需求的相關性進行移除，節點與的相關性表達式為：其中，ω1、ω2、ω3表示的是距離、時間窗和物料需求的權重系數，R（i，j）越大表示節點的相關性越小。

（2）貪心破壞算子，一次移除一個節點，選擇移除后成本降低最多的節點。每次移除節點前，計算當前總成本，并與移除每個可能節點后的新成本進行比較。選擇使總成本降低最多的節點進行移除。

（3）隨機破壞算子，隨機選取一定數量的節點，并將這些節點從其所在的路線中刪除。

（4）后悔插入算子，評估每個被移除節點插入任何位置的“后悔值”，選擇當前具有最大后悔值的節點進行插入，目的是避免過早做出可能限制未來選擇的決策，不僅考慮當前的最佳插入位置，還考慮對未來選擇的潛在影響。

其中，Va是某節點插入后的成本，Vb是某節點插入前的成本，VI是插入成本，min2VI表示次佳插入成本，minVI表示最佳插入成本，最大后悔值VR是次佳插入成本min2V和最佳插入成本minVI之差。

（5）貪心修復算子，對于每個被移除的節點，考慮所有可能的插入位置，并選擇使總成本增加最少的位置進行插入。

（6）隨機修復算子，將之前被破壞的節點隨機插入回路線中。對于每個被移除的節點，隨機選擇一條路線和該路線上的位置，并將節點插入到該位置。

3 實驗分析

以某離散制造車間為案例，并使用改進的ALNS算法進行求解。該車間有1 個車間倉庫、6 臺數控車床、3 臺數控銑床、1 臺數控鏜床、4 臺鉆床、3 個檢測臺，總計1 個車場和17 個需求節點，另有路徑拐點10 個，如圖5 所示。

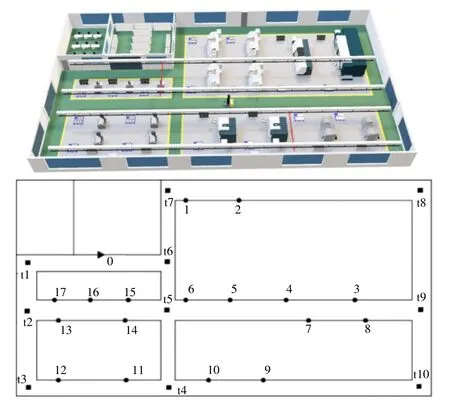
圖5 離散制造車間模型

車間工位位置、需求和時間窗等信息和拐點位置信息見表2，其中節點0 表示車間倉庫，t1 -t10 為車間拐點。首先，利用節點坐標、拐點坐標和車間路徑圖，根據之間聯通的節點（拐點）建立初始距離矩陣，并使用Floyd 算法得出個節點之間的最短距離矩陣，見表3。

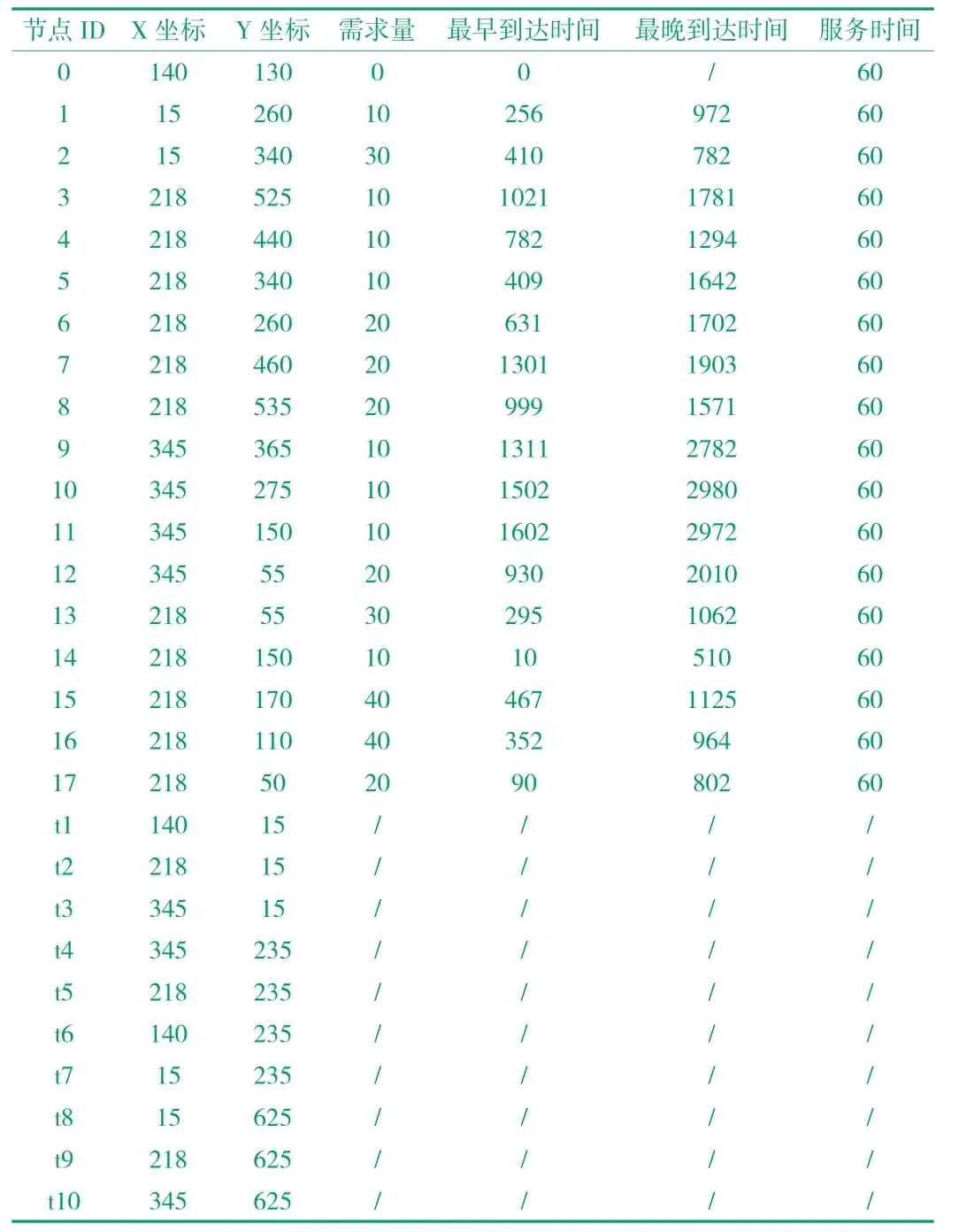
表2 節點需求信息

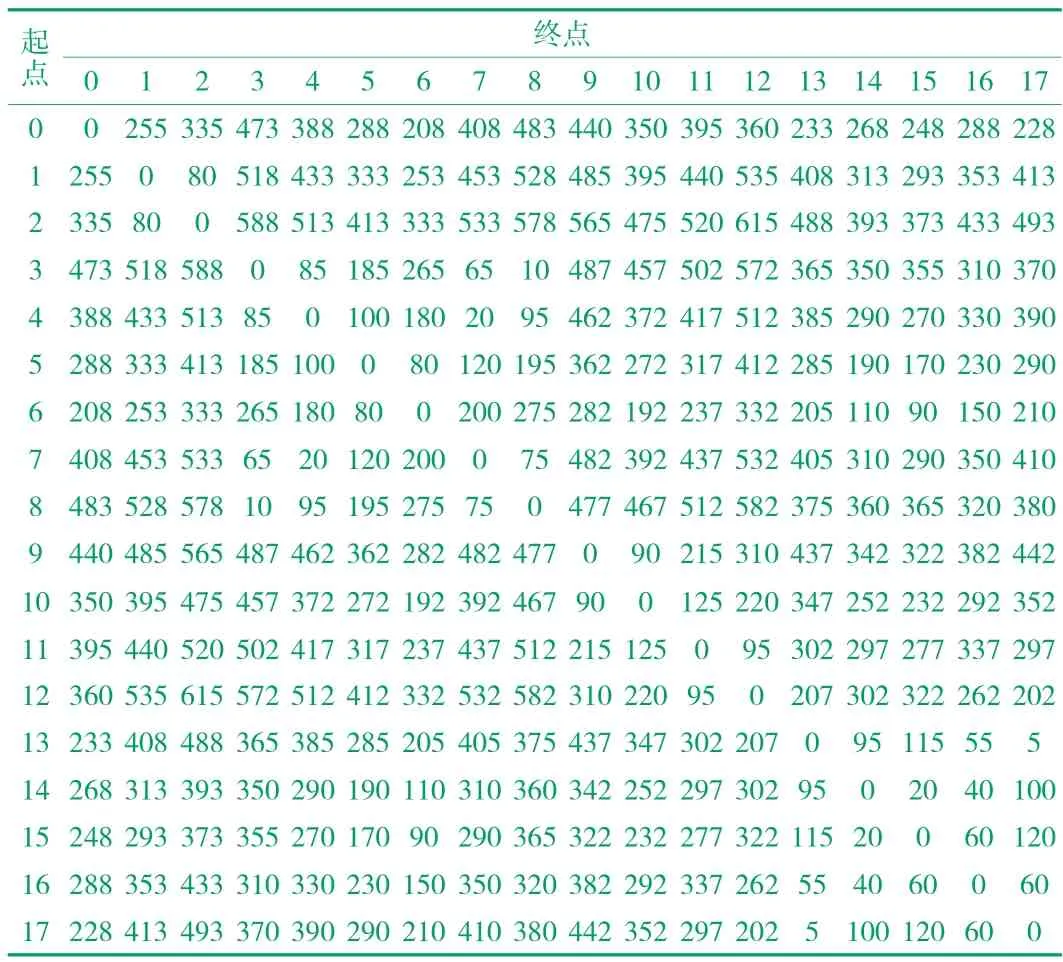
表3 節點最短路徑矩陣

本實驗使用IDEA2021，CPU 為12600 k，利用ALNS 算法結合模擬退火，實驗部分參數設置為：溫度下降率0.99，最大迭代次數400，超載懲罰系數γ=1000，時間窗提前懲罰系數α=10，時間窗超期懲罰系數β=2，可提供的最大運力車輛為3，破壞算子和修復算子初始權重相等。

從表4 和圖6 可知，在相同迭代次數下，ALNS 加入模擬退火后，求解時間略高于ALNS，但總體速度接近，可以滿足車間物料配送的決策實時性，在求解時間接近的情況下跳出局部最優，獲得成本更低的解。實驗結果表明，該方法能夠有效規劃物料配送路徑，減少配送時間和成本，并確保物料按時供應，提高了生產效率。

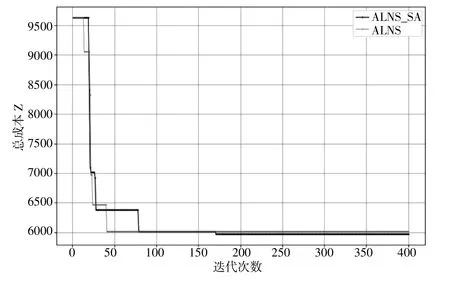
圖6 收斂曲線對比

表4 基于車間路徑約束的配送路徑序列

4 結語

本研究通過構建離散制造車間物料配送路徑優化的數學模型，并基于自適應大領域搜索（ALNS）算法進行了求解，有效地解決了多品種、小批量生產模式下的物料配送問題。實驗結果表明，該模型能夠有效地規劃物料配送路徑，減少配送時間，確保物料按時供應，同時降低物料配送成本。此外，通過引入車間路徑約束、時間窗和車輛容量限制，模型更貼近實際生產環境，提高了其應用價值。未來的研究可以在此基礎上同時取送貨的車間道路約束下的車輛路徑問題，以及考慮動態車間環境下的物料配送路徑優化問題，引入實時數據反饋和機器學習技術。