電網多源異構缺失數據最優投影整合算法研究

楊 晶,妥建軍,李 昊,廖 翯,馬雅蓉

(國網甘肅省電力公司發展事業部(經濟技術研究院),甘肅 蘭州 730046)

0 引言

隨著智能電網的持續發展,電力數據量不斷增加。電網大數據主要包括公共安全數據、在線監測數據[1-3]、調度運行數據和生產管理數據等。然而,由于這些基本數據的建模標準來源不同,導致數據類型存在差異,并且信息共享度較低,數據之間缺乏足夠的交互。這一問題導致電網數據具有高度異構和多源等特征,給數據的管理和應用帶來了巨大挑戰[4-6]。為了有效監測和管理電網,有必要對電網多源異構數據進行整合。首先,數據的異構性導致數據結構和格式存在差異,需要作統一處理和標準化,以便數據的集成和分析。其次,不同數據源之間的信息共享度低導致數據的冗余存儲和浪費,因而需要建立有效的數據交換和共享機制。此外,多源數據的整合還需解決數據質量和一致性的問題,包括數據異常值的檢測和清洗,以及數據間關聯性的建立和驗證。為了解決上述問題,研究人員提出了包括數據挖掘、機器學習和人工智能等的一系列電網多源異構數據整合方法。這些方法可以通過對數據的預處理、特征提取和數據融合等步驟,實現對電網多源異構數據的整合分析和管理。同時,還需要考慮數據安全和隱私保護的問題,確保整合后的數據在使用和傳輸過程中不會泄漏敏感信息。電網多源異構數據的整合是實現電網智能化管理的重要步驟,需要綜合運用各種技術手段解決數據的異構性、冗余性和安全性等問題。通過有效的整合和分析,可以更好地實現對電網的監測和管理,提高電力系統的可靠性、安全性和經濟性。

近年來,很多學者針對多源異構數據進行了研究。莫慧凌等[7]根據張量Tucker分解理論,在無交互條件下建立高階張量算法。該算法具有異構空間維度特性,可以提取數據的高維特征,故以此為依據可實現多源異構數據的整合。但是該算法無法消除多源異構數據中存在的噪聲,且存在數據處理效果差的問題。趙春霞等[8]提出了一種基于極大元法和關聯規則的數據挖掘方法,通過建立相異度數據結構矩陣來挖掘數據集中的最大頻繁項。該方法利用平均加權法計算異構數據的特征,并通過高維相空間重構和時間反轉處理,以實現多源異構數據的整合。然而,該方法在整合缺失數據時存在精度低的問題。張騰飛等[9]提出了一種基于粗糙模糊的K-means聚類算法。該算法考慮了類簇規模的不均衡程度,并引入自適應度量。通過對人工數據集和加州大學歐文分校(University of California Irrine,UCI)標準數據集的驗證,證明了該算法的有效性。然而,該算法在數據處理方面可能存在誤差。郭方方等[10]提出了一種基于有監督判別投影的網絡安全數據降維算法。該算法利用近鄰矩陣和類別標簽信息構建有監督判別矩陣,并通過尋找最大全局散度矩陣和最小局部散度矩陣的低維投影子空間來實現降維。然而,該方法可能存在判別精度低的問題。

基于上述文獻,本文提出一種針對電網多源異構缺失數據的最優投影整合算法。該算法創新性地引入拉格朗日差值方法填充缺失值,采用經驗模態分解方法消除噪聲,并建立投影指標函數將高維數據轉換為一維投影值。該算法通過數據填充和去噪來提高電網多源異構數據的完整性和準確性,并利用混沌文化差分進化算法尋找最優投影方向,從而完成缺失數據的整合。該算法不僅具有較好的數據去噪效果,并且能夠提高數據的整合精度和穩定性,有助于提升電網多源異構數據的質量和管理水平。

1 電網多源異構數據集中整合

1.1 野值數據修正與填充

傳感器在電網中具有不同的采樣周期,導致電網數據的時間存在不匹配的情況。網絡延遲會對數據采集產生影響,導致整合中心與電網傳感器之間的數據采集周期存在差異。為了提高數據整合的精度,需要對不同步的數據開展時間配準。在對電網多源異構數據開展配準之前,需要對數據中存在的野值進行檢測。本文對閾值和修正值檢測數據中存在的野值進行修正。修正后的結果v(k)為:

(1)

式中:rnew(k)為電網數據;C為野值判斷參數;X(k)為第k個指標對應的修正值。

真實估計值對應的權重μ(k)可在v(k)的基礎上通過加權函數獲得。

μ(k)=el(k)v(k)

(2)

式中:l(k)為第k個指標加權函數;e為自然對數。

xi=Xn+TXn(i-n)+bi

(3)

式中:Xn為第n個測量序列;bi為電網多源異構數據中存在的噪聲,dB。

傳感器B采集的數據構成的測量向量En為:

(4)

式中:T′為數據整合時間,s。

通過上述過程完成電網數據的配準,獲得高精度的電網多源異構數據。

為了確保電網多源數據密度的一致性,本文采用拉格朗日差值方法[13-14]填充電網時序數據,并采用拉格朗日差值函數F(t)填補電網時序數據tj。

(5)

式中:zj(t)為第j個差值基函數;ts為時序數據s對應的時間,s。

1.2 電網多源異構數據去噪

本文以修正與填充后的電網多源異構數據為基礎。為了提高后續的集中整合質量,本文采用經驗模態分解方法對多源異構數據作去噪處理。信號c(t)在電網多源異構數據中的功率Ax為:

(6)

式中:N為信號的數量,個。

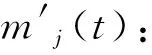
(7)

采用經驗模態分解方法對電網多源異構數據進行去噪的具體過程如下。

①采用經驗模態分解方法對含噪的電網多源異構數據信號c(t)展開分解,獲得q個IMF分量。

1.3 多源異構數據集中整合算法設計

對完成濾波處理的電網多源異構數據開展集中整合的具體過程如下。

①采用式(8)標準化處理預處理后的電網多源異構數據Cj={c1j,c2j,…,cMj}。

(8)

式中:cimax、cimin為數據i對應的最大值和最小值;rij為標準化處理后的數據。

②建立投影指標函數WF(a)。

(9)

式中:F(y)為兩個樣本點在每扇窗內的距離;D(y)為樣本投影值對應的標準差;R(y)為單位階躍函數。

根據投影指標函數WF(a),即可建立電網多源異構數據的聚類中心。

③高維電網多源異構數據經過投影處理后轉變為一維的投影值。此時,維度M=1,存在權重w=1。電網多源異構數據的聚類中心dh和隸屬度uhj為:

(10)

式中:rj為數據對應的特征值;c為電網多源異構數據種類的數量,個。

④模糊聚類迭代適應度G(uhj,dh)為:

(11)

如果適應度符合min{G(uhj,dh)}條件,則執行步驟⑤;否則,采用混沌文化差分進化算法搜索電網多源異構數據的最優聚類中心,并返回步驟③。

⑤利用混沌文化差分進化算法尋找電網多源異構數據的最優投影方向。

⑥通過式(12)計算電網多源異構數據的連續性類別特征值V(j):

(12)

式中:h為電網多源異構數據的類別。

根據式(12)計算結果對電網多源異構數據排序,獲得數據的聚類結果,從而完成電網多源異構數據的整合。

采用迭代模糊聚類算法集中整合的電網多源異構缺失數據最優投影整合算法流程如圖1所示。

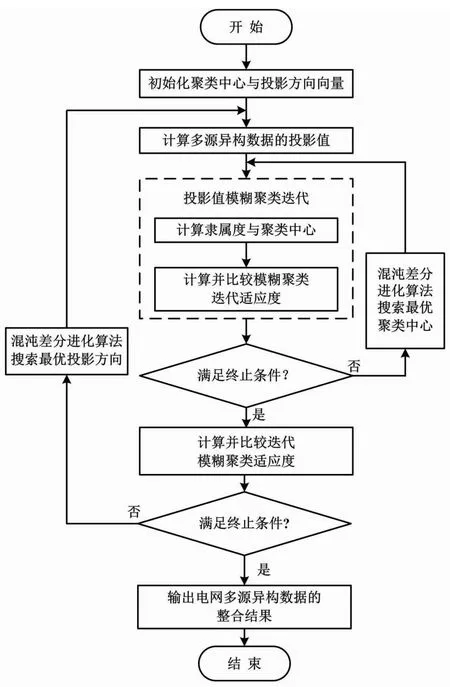
圖1 電網多源異構缺失數據最優投影整合算法流程圖

2 試驗與分析

為了驗證本文算法的整體有效性,需要對該算法進行測試。電網多源異構數據在采集過程中受多種因素的影響,導致數據中存在噪聲,影響數據的整合效果。

含噪電網多源異構數據如圖2所示。

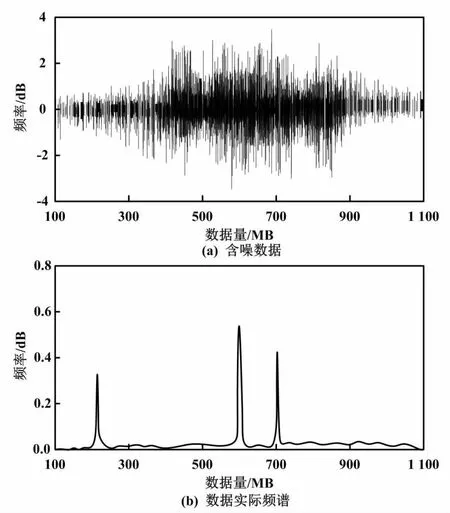
圖2 含噪電網多源異構數據

本文采用本文算法、張量Tucker分解整合算法(文獻[7]算法)、平均加權整合算法(文獻[8]算法)對圖2所示的含噪電網多源異構數據作去噪處理。

本文算法的降噪處理結果如圖3所示。

圖3 本文算法的降噪處理結果

文獻[7]算法的降噪處理結果如圖4所示。

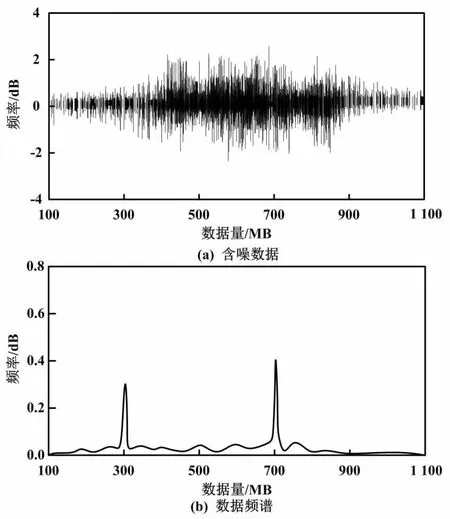
圖4 文獻[7]算法的降噪處理結果

文獻[8]算法的降噪處理結果如圖5所示。

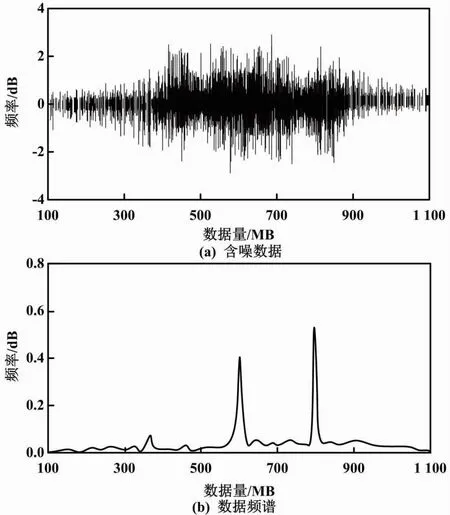
圖5 文獻[8]算法的降噪處理結果

由圖3～圖5可知,采用本文算法進行去噪處理后,含噪數據的波動頻率明顯降低,而文獻[7]算法與文獻[8]算法經降噪處理后,含噪數據的波動頻率仍然保持較高的水平。這說明本文算法去噪效果較好。觀察三種算法去噪后的數據頻譜可以看出,相較于原始頻譜,文獻[7]算法與文獻[8]算法去噪后數據頻譜與原始頻譜相差較大。這說明兩種對比算法的降噪處理出現了一定程度的失真。而本文算法的去噪頻譜與原始頻率基本一致,說明本文算法并不會出現失真的情況,可以確保電網數據的完整性。

電網多源異構數據量較為龐大,對算法的時間復雜度提出了更高的要求,即要求整合算法能夠在較短的時間內處理大量的缺失數據。因此,本文以時間復雜度為指標,將本文算法、文獻[7]算法、文獻[8]算法進行對比驗證。

不同算法的時間復雜度對比結果如表1所示。

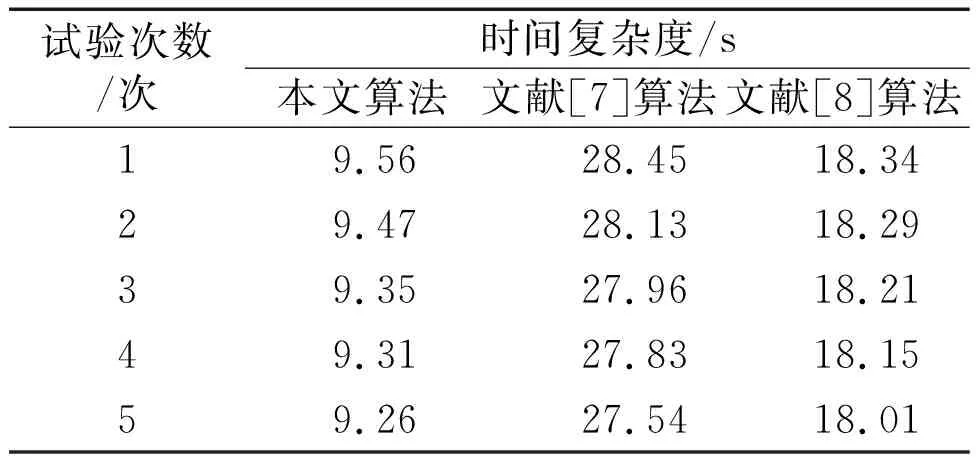
表1 不同算法的時間復雜度對比結果

由表1可知,隨著試驗次數的增加,三種算法的時間復雜度出現了明顯的差距。其中:本文算法的時間復雜度最高未超過10 s;文獻[7]算法的時間復雜度是三種算法中最高的,達到28.45 s;文獻[8]算法的時間復雜度也高于本文算法,基本在18 s左右。這說明本文算法的時間復雜度明顯下降,數據整合的效率提高。

算法在開展數據整合的過程中,其穩定性不可忽略。穩定性越強,則實際應用的可靠性越高。

不同算法的整合精度結果如圖6所示。

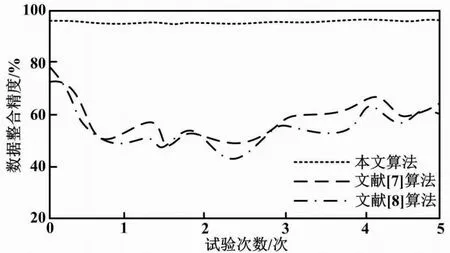
圖6 不同算法的整合精度結果

由圖6可知,三種算法中,本文算法的數據整合精度最高,且隨著試驗次數的增加,并未出現明顯的波動。這說明該算法可以在提高數據整合精度的同時,確保自身運算的穩定性。觀察兩種對比算法可以看出,兩種對比算法的數據整合精度最高均未超過80%,并且波動范圍較大。這說明兩種對比算法的穩定性略低于本文算法。

算法的收斂性指算法能否在迭代時間趨于無窮的假設下,找到問題的全局最優解。收斂性作為算法能否使用的關鍵性能,直觀地體現了算法的可用性。因此,本文對三種算法的收斂性進行驗證。

不同算法的收斂性結果如圖7所示。

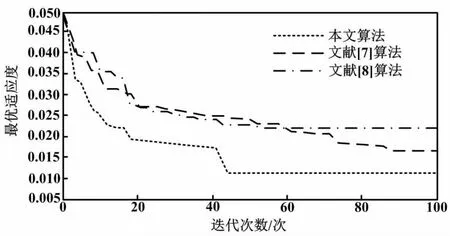
圖7 不同算法的收斂性結果

由圖7可知,本文算法在三種算法中收斂速度最快,且最優適應度值最低。文獻[8]算法的前期雖然收斂較快,但是最優適應度值較高。由此說明本文算法的收斂性較好。

3 結論

針對目前電網多源異構數據整合方法中存在的數據處理效果差、整合精度低的問題,本文提出針對電網多源異構缺失數據的最優投影整合算法。該算法對數據開展了修正、填補和去噪處理,并在此基礎上通過迭代模糊聚類算法實現電網多源異構數據的集中整合。測試結果表明,本文算法可有效消除數據中存在的噪聲,并且可以確保去噪后電網多源異構數據的質量,以避免出現失真情況。本文算法的整合精度、穩定性以及收斂性均優于其他對比算法,整合精度始終穩定在95%左右。