基于目標滑移率的車輛防抱死制動系統控制算法研究

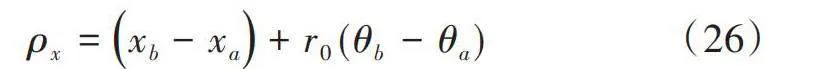
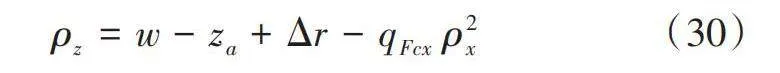
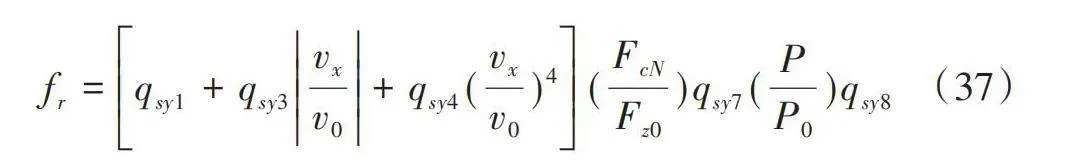
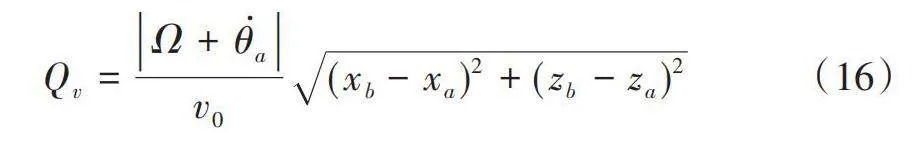
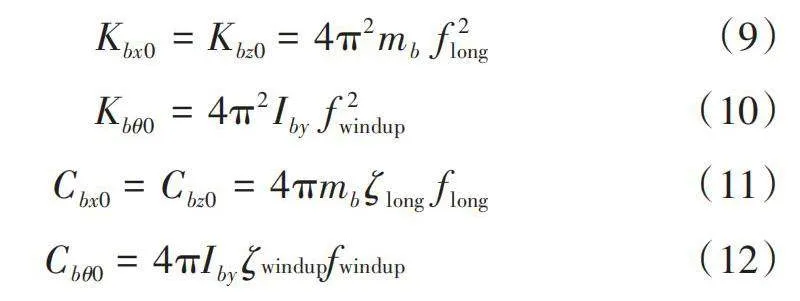
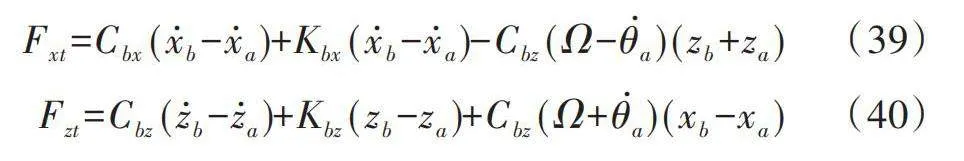
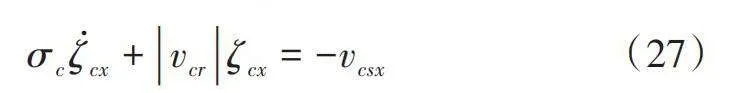
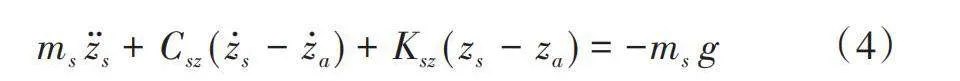
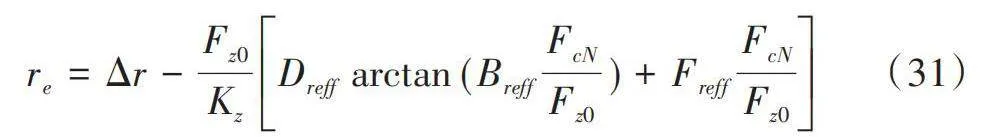
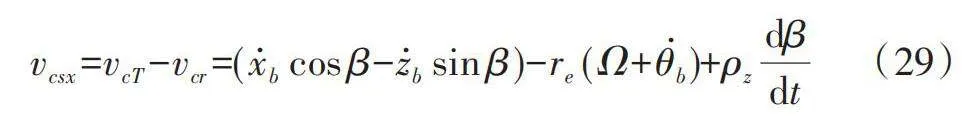
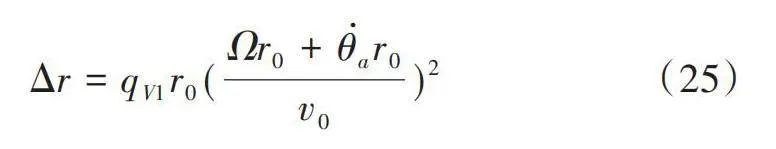
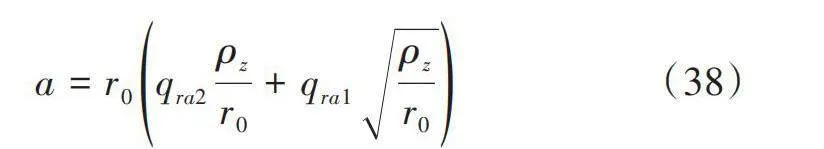
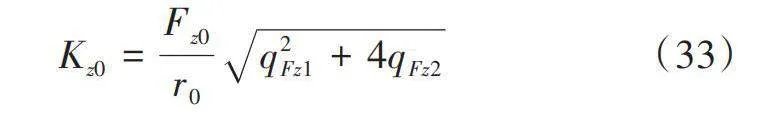
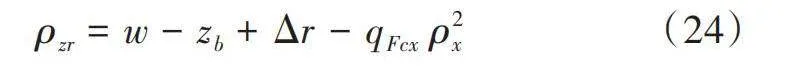
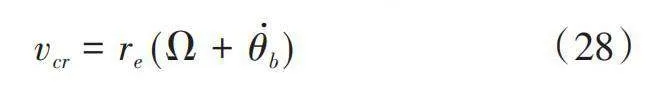
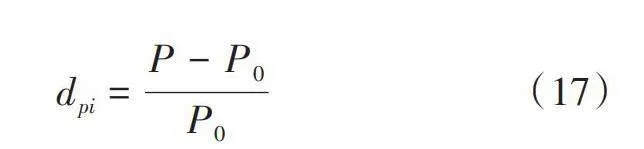
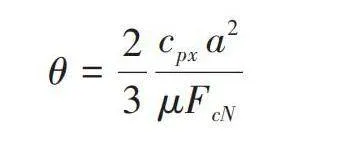
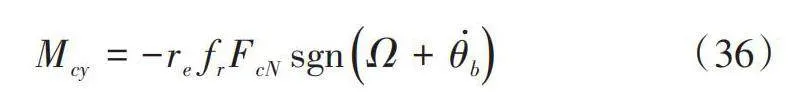
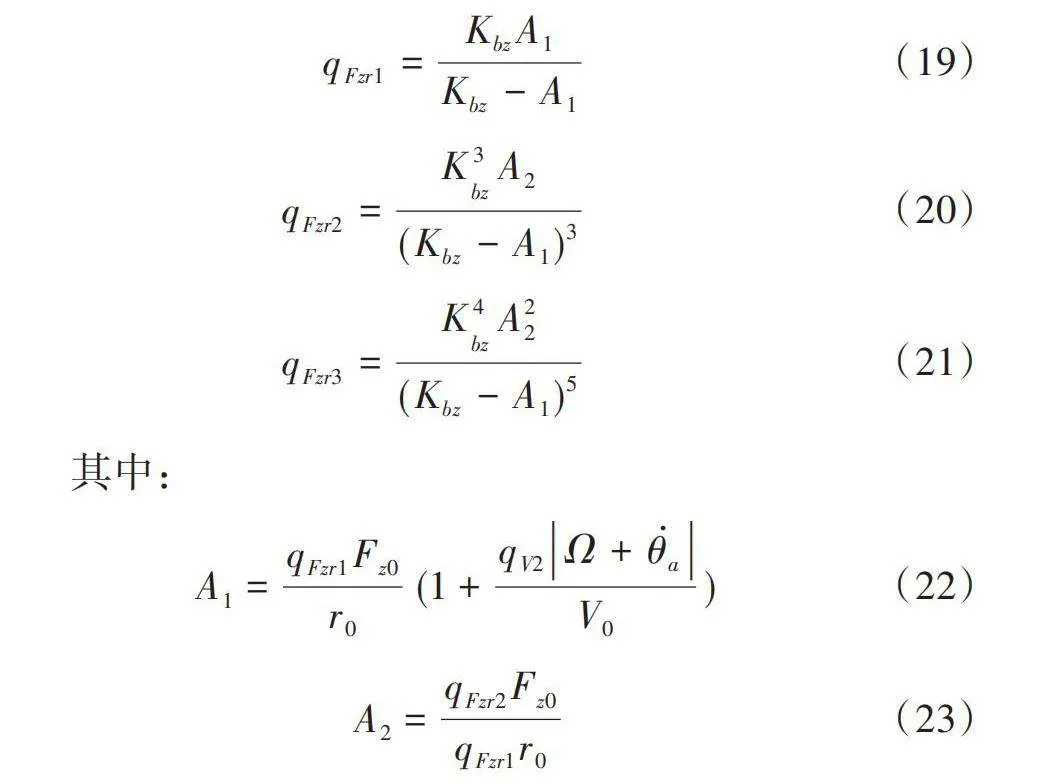
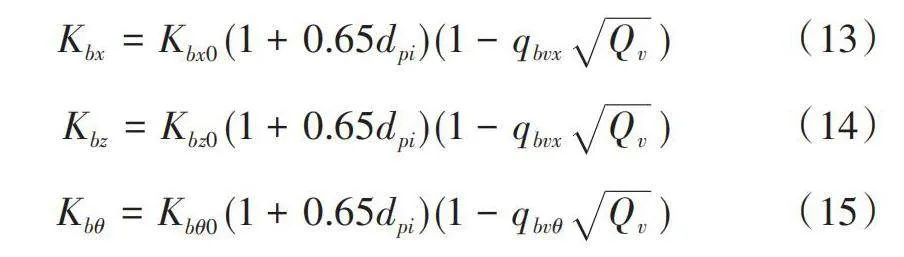
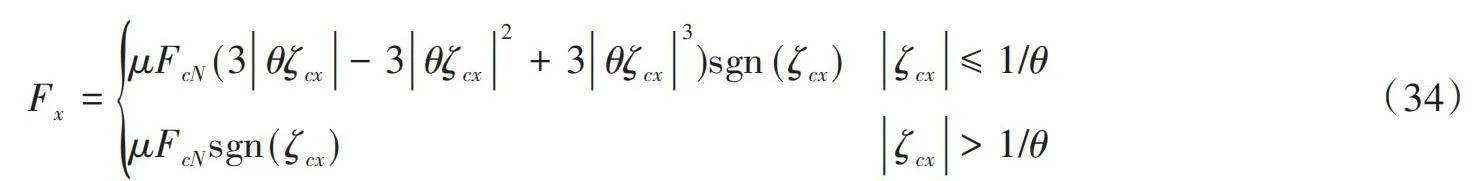
摘要：建立了包含平面內SWIFT輪胎模型在內的四分之一車輛模型，建立了防抱死制動系統模型，并設計了以車輪滑移率為目標，采用PID控制的ABS算法。基于該平臺對ABS控制算法進行仿真，驗證其合理性。最后將ABS控制算法的代碼集成到電控制動系統中進行實車試驗，試驗結果表明，基于目標滑移率的ABS控制算法滿足預期。

關鍵詞：目標滑移率；PID控制；防抱死制動系統；SWIFT輪胎模型

中圖分類號：U463.5 收稿日期：2024-02-22

DOI：10.19999/j.cnki.1004-0226.2024.04.010

1 前言

目前，車輛防抱死制動系統（ABS）作為汽車重要的組成部分，已經發展成為成熟產品，并廣泛應用于各種車輛。其通過調節制動壓力來控制車輛滑移率在一定的范圍之內，不但減小制動距離，同時也保證了汽車的轉向能力和穩定性，從而保護了駕駛員的安全[1]。目前ABS控制算法主要包括邏輯門限值控制和基于目標滑移率控制等。邏輯門限值控制是ABS經典控制算法，其通過車輪的減速度和滑移率來對車輪進行增壓、保壓和減壓循環控制，使得車輪滑移率在目標附近波動。這種方法可靠簡單，多用于量產的ABS產品中。

由于整個制動過程中車輪滑移率不能一直保持在最佳滑移率上，而是在其附近波動，因而邏輯門限值控制算法未能達到最佳的ABS制動性能。為了進一步提高整車的ABS制動性能，基于目標滑移率控制算法被提出，并且被廣泛研究[2]。

2 仿真驗證平臺搭建

2.1 四分之一車輛模型

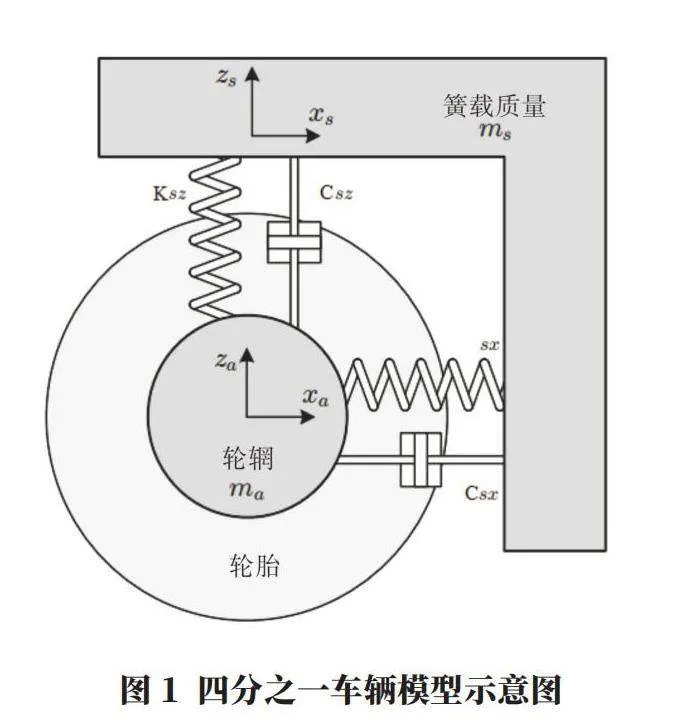
四分之一車輛模型常用于乘坐平順性和制動性能研究。這里考慮的模型假設懸架在X和Z方向上都具有順應性，具有簧載質量的縱向運動xs、簧載質量的垂向運動zs、輪輞的縱向縱向運動xa、輪輞的垂向運動za四個自由度，該模型的輸入是從動態輪胎模型到輪輞的反作用力構成。模型輸出是作為輪胎模型輸入的車軸運動。四分之一的車輛模型如圖1所示。

根據牛頓定律，四分之一車輛模型的運動方程為：

式中，Ksx和Ksz、Csx和Csz分別為沿X方向和Z方向的懸架剛度和阻尼值；ms為汽車的簧載質量；ma為由包括懸架和制動元件在內的非簧載質量。假設懸架剛度和阻尼元件是線性的，并且沿X軸和Z軸的變形是相互獨立的。

2.2 平面內SWIFT模型

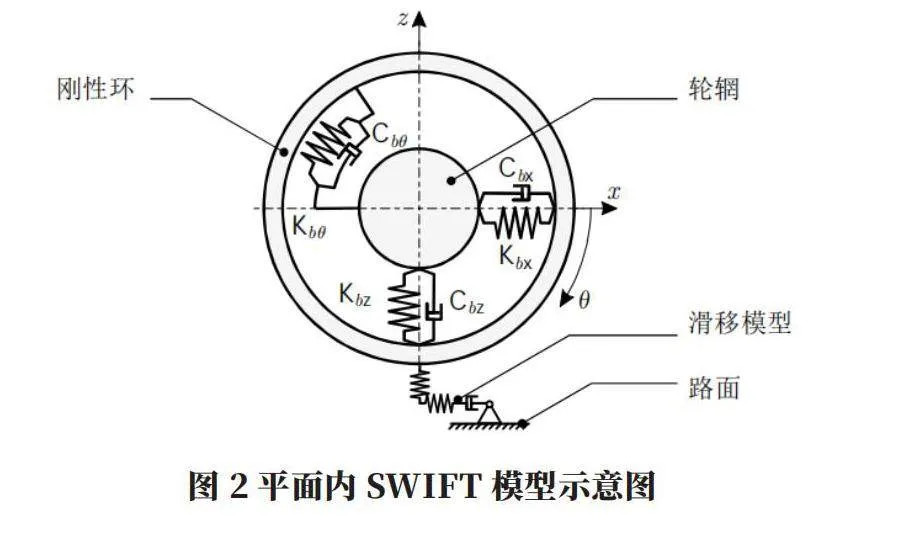
如圖2所示，剛性環模型具有環的水平運動xb，環的垂直運動zb，環的扭轉運動θb，以及輪輞的扭轉運動θa四個自由度。滾動輪胎的動力學通過一組非線性二階微分方程來表示。

根據牛頓定律，車輪模型的運動方程為：

其中，環模型的慣性參數是通過實驗測量的，剛性環質量用mb表示，其繞Y軸的慣性矩用Iby表示。慣性矩Iay由輪輞和制動卡鉗的轉動慣量構成。

2.2.1 胎體剛度與阻尼

胎體的縱向剛度、垂直剛度以及旋轉EqhM6xEFCGrPo4Ky0Eu2o00JVW1Ke2vUMLx5uwzdRtI=剛度和阻尼是由平面內剛性環模態的固有頻率計算出來的。胎體剛度和阻尼值的計算方法為：

式中，flong和ζlong是剛性環的垂直以及縱向運動的特征頻率和阻尼因子，fwindup和ζwindup是剛性環旋轉運動的特征頻率和阻尼因子。下標“0”表示非滾動條件下輪胎的剛度和阻尼值。式（8）僅適用于胎體為剛體時，在這種情況下，輪胎做剛體運動。根據Zegelaar [3]之前的研究，可以知道滾動輪胎的固有頻率隨速度變化，因此，實際的胎體剛度遠遠低于使用公式（9）和（10）計算得到的值。為了考慮這種影響，通過修正系數使胎體剛度依賴于滾動速度、壓力和垂直載荷：

式中，變量Qv為無維度變量，表示輪胎因滾動而引起的變形率，用以下關系計算：

式中，v0為標稱滾動速度。利用試驗標定考慮胎體剛度的壓力依賴性。變量dpi表示測量的輪胎壓力的變化率：

式中，P0為標稱輪胎壓力；P為當前輪胎壓力。

2.2.2 接觸區法向載荷

接觸區中的法向力用FcN表示，是接觸區中的殘余剛度和殘余變形的乘積[4-5]。由于輪胎的總變形大于剛性環的垂向位移[6]，因此總垂直剛度是胎體剛度Kbz和殘余剛度的串聯組合。接觸區中的法向力與參與變形呈非線性關系，表示為以下三階多項式：

式（18）中的多項式系數由胎體剛度Kbz、參數qFz1、qFz2計算，它們是總垂直載荷-垂直變形特性的函數：

其中：

常參數Fz0為標稱的垂直載荷；r0為非滾動條件下的自由輪胎半徑。因子qV2解釋了垂直剛度隨速度的增加，Ω是輪輞的轉動角速度。接觸塊內的法向力受到有效道路高度分布、剛性環垂向和切向偏轉的影響，這些因素通過殘余變形計算：

這里，qFcx是一個模型待標定參數，變量[Δr]表示由于滾動引起的自由輪胎半徑的增長：

式中，qre0和qV1為可以估計的模型參數。

在較高的制動扭矩和恒定軸高下受水平偏轉ρx的影響，計算公式為：

2.2.3 滑移模型

作用于接觸區中的切向力用FcT表示。切向作用力是由于在接觸中發生滑移ζcx而產生的。滾動輪胎的胎面與地面之間的動態相互作用導致滑移的變化。此外，滑移還受到胎體變形和有效滾動半徑的變化的影響。這對ABS系統的設計分析起著至關重要的作用，因此，胎面元素需要通過接觸模型來模擬瞬態滑移。其中的非穩態滑移變化采用一階近似進行建模，該近似基于松弛長度σcx和環運動計算出的滑移速度：

式中，σc為接觸區的松弛長度，滑移ζcx是有限的，以避免數值穩定性問題。環的直線滾動速度vcr計算為：

vsx為環相對于路面的滑移速度，此外還需考慮道路擾動對有效滾動半徑的影響。計算公式為：

其中，ρz為輪胎的總垂直偏度：

2.2.4 有效滾動半徑

為了計算滾動速度，需要得到有效滾動半徑范圍，通過經驗關系計算：

式中，Breff、Dreff和Freff為模型參數。與輪胎壓力相關的總垂直剛度Kz通過以下關系式計算：

式中，ρFz1為垂直剛度與輪胎壓力的線性依賴關系；Kz0為輪胎的標稱垂直剛度，由以下公式計算：

2.2.5 輪胎-路面切向作用力

方程（27）的滑移模型可以得到的瞬態滑移ζcx值和式（18）中得到的接觸區中的垂直載荷FcN作為刷子模型的輸入，從而計算接觸區中的切向力FcT。刷子模型是一個穩態物理輪胎模型，其中假設胎面元素具有剛毛的行為，單位長度的胎面剛度為cpx，切向力FcT計算公式為：

式中，[μ]為路面摩擦因數，復合參數θ被定義為：

2.2.6 松弛長度

式（27）中使用的松弛長度σc由局部滑移剛度Ck和自由滾動Ck0下的滑移剛度計算得出：

式中，[Ck0=2cpxa2]，[Ck=（?Fx?ζ）ζ=ζcx]，σc0為自由滾動時的松弛長度，等于接觸長度的一半。自由滾動的滑動剛度Ck0下由單位胎面剛度cpx和接觸長度a計算。

2.2.7 滾動阻力

滾動阻力是輪胎在路面上滾動時的阻力。滾動阻力Mcy計算公式為：

式中，fr為滾動阻力系數。假設該系數以速度的非線性多項式函數變化，并表示為：

式中，參數qsy1、qsy3、qsy4、qsy7、qsy8通過試驗標定得出。

2.2.8 有效接觸長度

當輪胎被加載時，變形導致輪胎與地面之間的接觸面變平。假設這個接觸區域為橢圓形狀，接觸區域隨著負載的增加而增大，假設接觸區域的長度與垂直載荷呈非線性關系，可以表示為：

式中，a為接觸長度的一半；qra1和qra1為通過試驗擬合得到的參數。

2.2.9 作用在輪輞上的力

輪胎在車軸上產生的力作為從輪胎模型到車輛模型的輸出，根據公式（5）和公式（6）可得作用在車軸上的力為：

2.3 防抱死制動系統模型

防抱死制動系統主要包括信號處理與PID控制模塊。信號處理模塊主要是對四個輪速信號處理：

a.輪速的過濾，去除輪速的噪音干擾，得到最終輪速（vwhl）。

b.通過對輪速的微分后過濾計算得到車輪加速度。

c.根據四個輪速估算得到整車的參考車速，且通過補償得到四個輪子的參考輪速（vref）。

d.根據不同的工況計算的車輪目標滑移率。

PID控制模塊主要是基于目標滑移率控制算法，具體如下：

a.通過目標滑移率計算車輪的目標輪速vtarget。

b.比較vwhl和vtarget大小，計算滑移率控制是否激活。

c.根據vwhl和vtarget之間的關系，來判斷車輪狀態（Slip_State：Above State和Under State）。

d.不同車輪Slip_State，結合附著系數和車輪的動態（速度和加速度等），設置不同的P（比例）和D（微分）系數。

e.在不同車輪Slip_State，結合附著系數和車輪的動態（速度和加速度等），設置不同的I（積分）系數；同時在特殊情況下（低到高），設置開環I項。

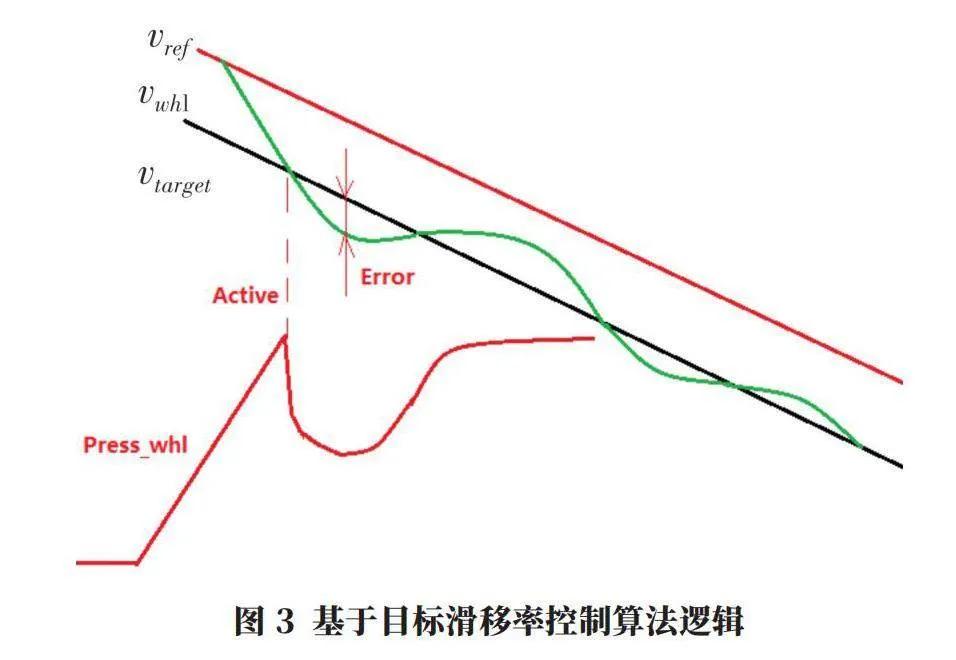
目標滑移率控制基本邏輯如圖3所示。

3 仿真平臺驗證與ABS算法測試驗證

在上文中，完成了四分之一車輛及其關鍵子系統模型搭建并基于目標滑移率開發了ABS算法，下面將首先對車輛及其關鍵子系統動力學模型合理性和準確性進行驗證，并在此之后驗證ABS算法的工作性能。

3.1 車輛及其子系統動力學模型驗證

3.1.1 輪胎垂直加載試驗

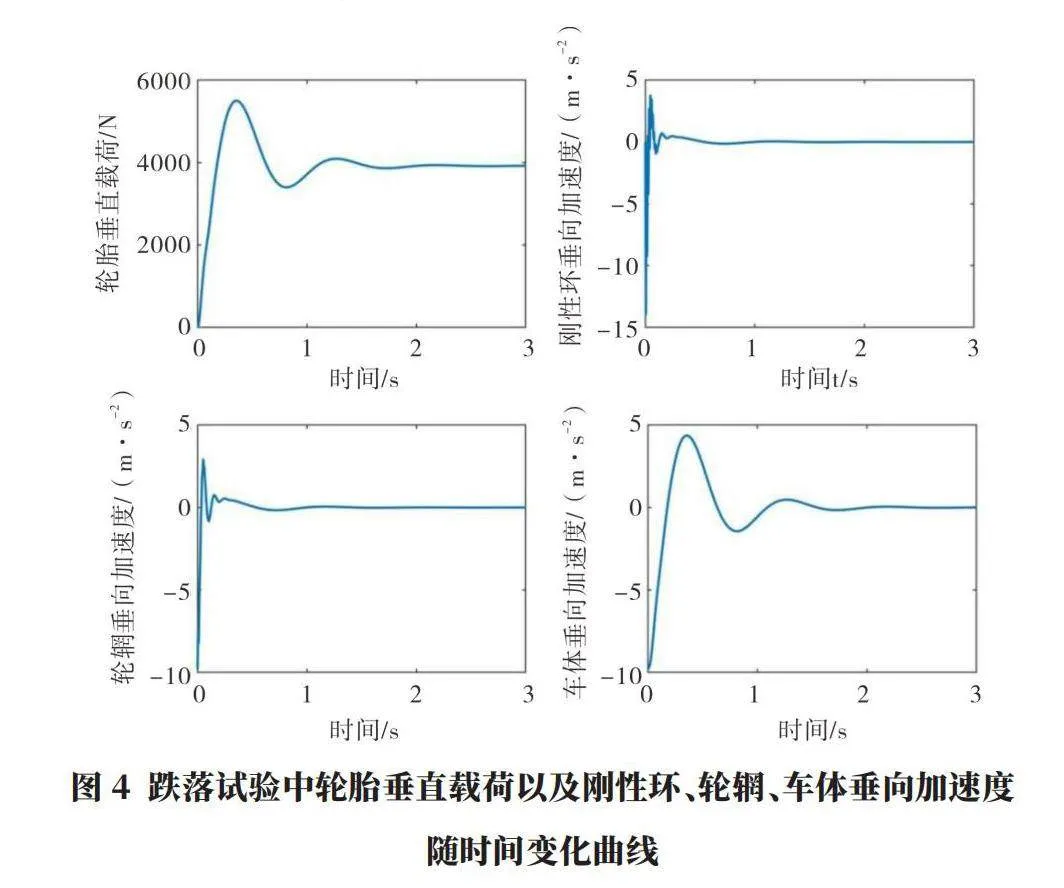
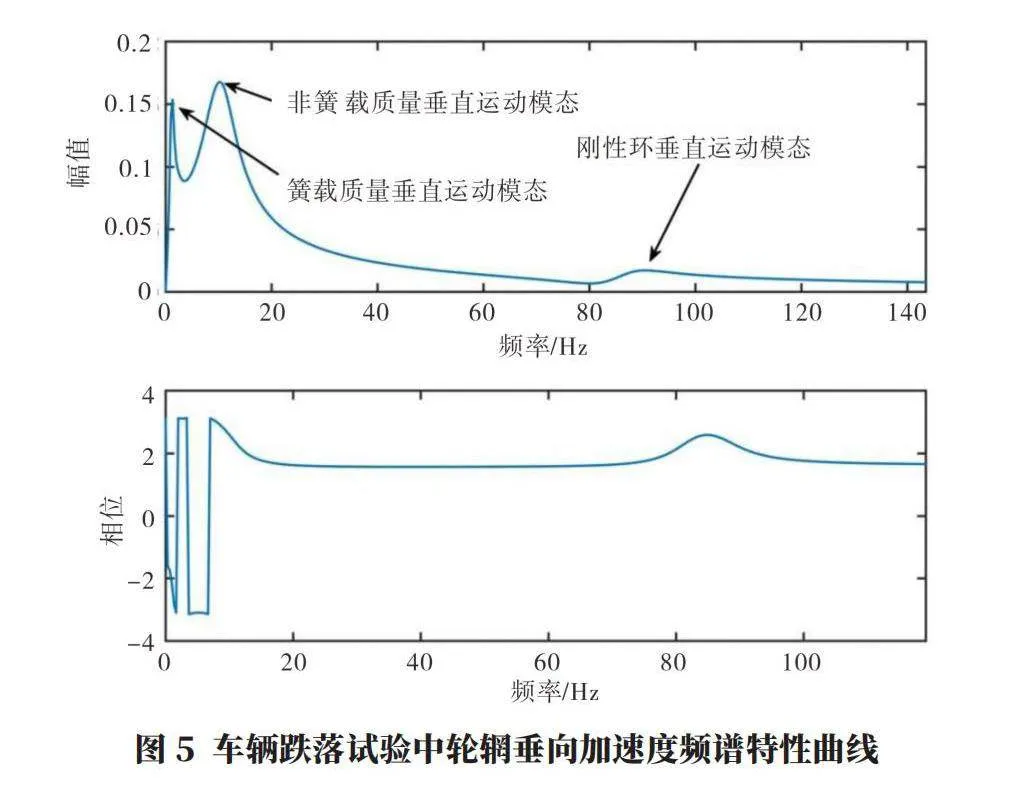
本文搭建的包含SWIFT輪胎模型四分之一車輛模型，理論包含了簧載質量、非簧載質量以及輪胎垂直運動模態，為驗證該部分模型的合理性與正確性，這里將四分之一車輛抬起至懸架與輪胎恰好無變形狀態，然后將車輛釋放，此時輪胎與路面接觸并且在垂直方向上的上述元件發生振動，如圖4所示，車體和輪輞的垂向加速度初始值為重力加速度，并且由于懸架和輪胎的順應性使得輪胎垂直載荷和車體/輪輞/剛性環以不同的頻率振蕩。進一步將輪輞處的垂直加速度-時間特性曲線通過快速傅里葉變換轉換為如圖5所示的頻譜圖，由該圖可知，在該信號中依次從低頻到高頻分別包含車體（簧載質量）的垂直運動模態（約為1.5 Hz）、輪輞（非簧載質量）的垂直運動模態（約為11 Hz）以及輪胎剛性環的垂直運動模態（約為90 Hz），該模型在垂直運動方向上運動與實際情況符合并與文獻報道基本一致，驗證在垂向運動建模的合理性以及正確性。

3.1.2 從靜止快速啟動試驗

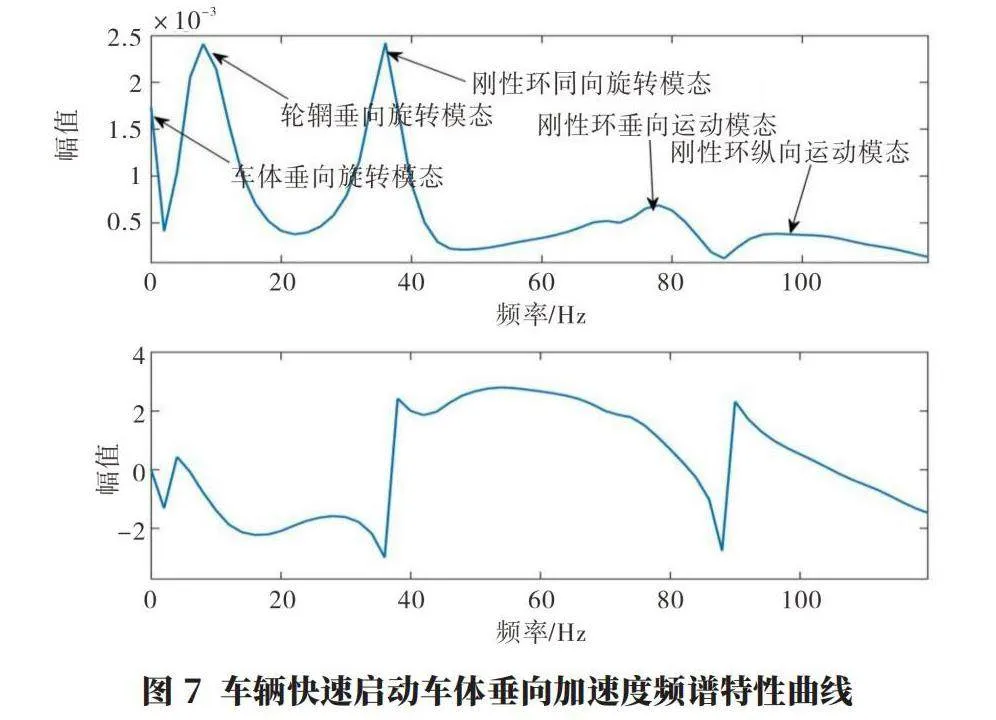
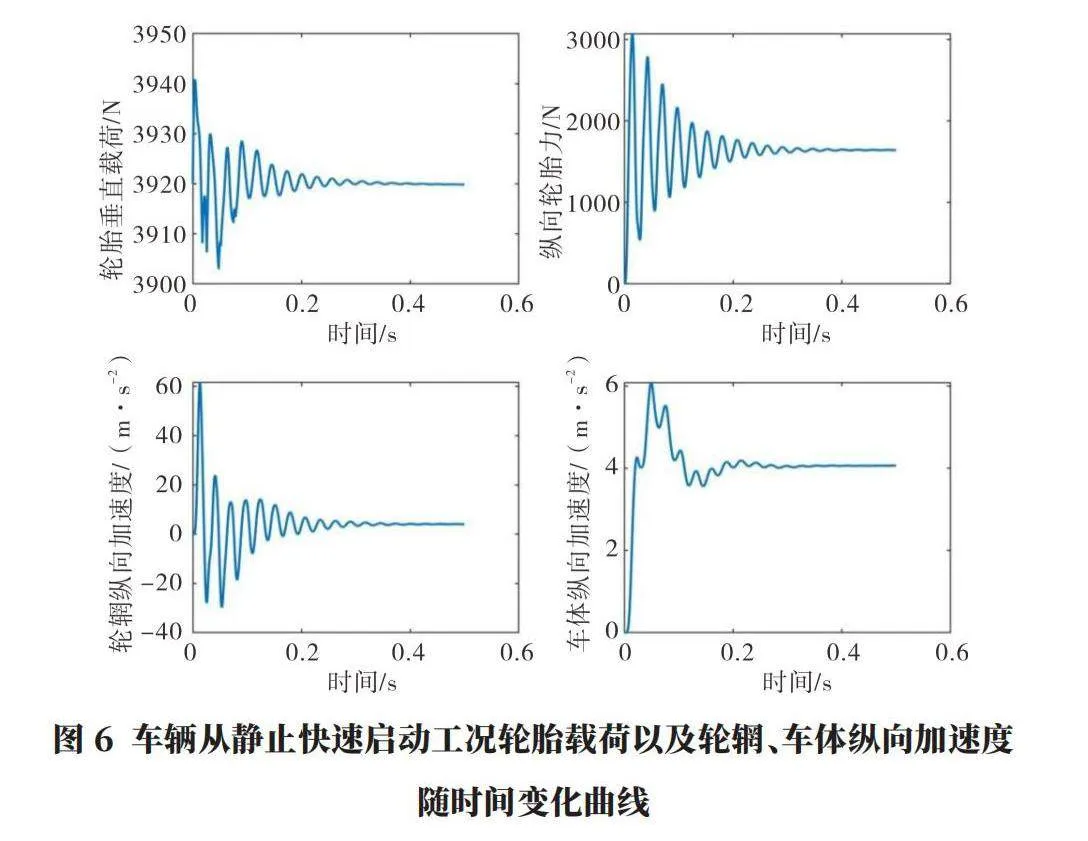
本文搭建的包含SWIFT輪胎模型四分之一車輛模型，理論上應包含車體、輪輞、輪胎縱向運動模態以及輪胎同向旋轉模態，為驗證該部分模型的合理性與正確性，這里考慮在靜止的車輛上施加500 N·m的階躍驅動力矩以仿真車輛快速啟動工況。如圖6所示，在階躍驅動力矩作用下，輪胎垂直載荷由于垂向振動而在穩態值附近小幅度波動，而縱向輪胎力在達到穩態值前由于輪胎旋轉方向順應性發生振蕩，并且振蕩通過輪胎和懸架縱向順應性傳遞至車體，會對乘員瞬時性產生負面影響，應給予消除。進一步將車體處的垂直加速度-時間特性曲線通過快速傅里葉變換轉換為如圖7所示的頻譜圖，由該圖可知，在該信號中除了上節跌落試驗中包含的各元件垂向運動模態外，還包含輪胎的同向旋轉模態（約為35 Hz）和縱向運動模態（98 Hz），該模型在垂直運動方向上運動與實際情況符合并與文獻報道基本一致，驗證了垂向運動建模的合理性和正確性。

3.2 ABS控制算法模型驗證

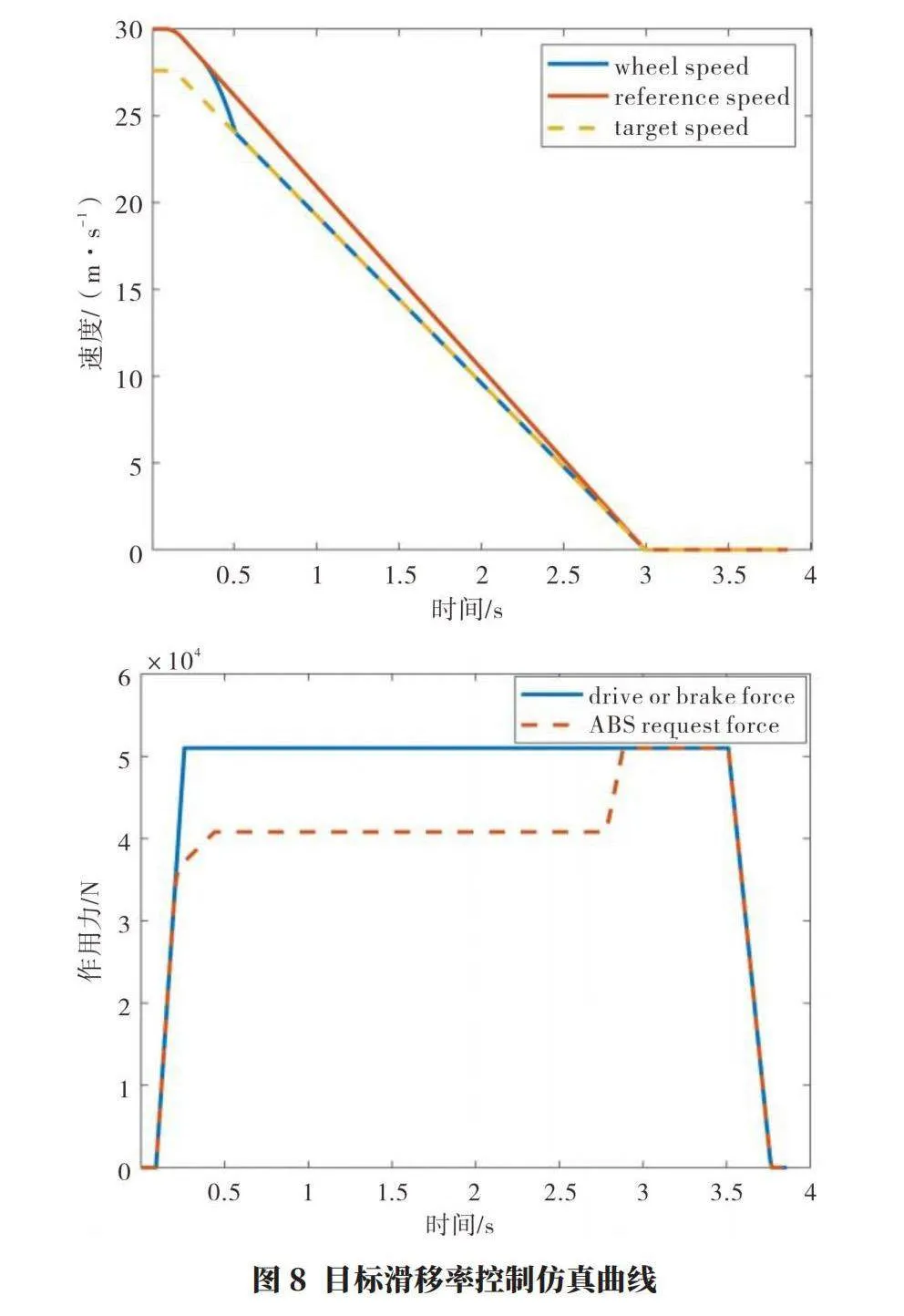
本節對設計的基于目標滑移率ABS控制算法進行驗證，車輛在初速度30 m/s條件下緊急制動，并在車速為3.0 m/s情況下逐漸退出ABS控制。如圖8所示，整個ABS過程中，輪速快速趨近目標車速，并緊跟目標輪速至車輛停止，ABS控制卡鉗（制動器）的夾緊力維持在40 000 N，充分地利用了路面最大附著力，整車峰值減速度1.05 g。

3.3 ABS控制算法實車試驗

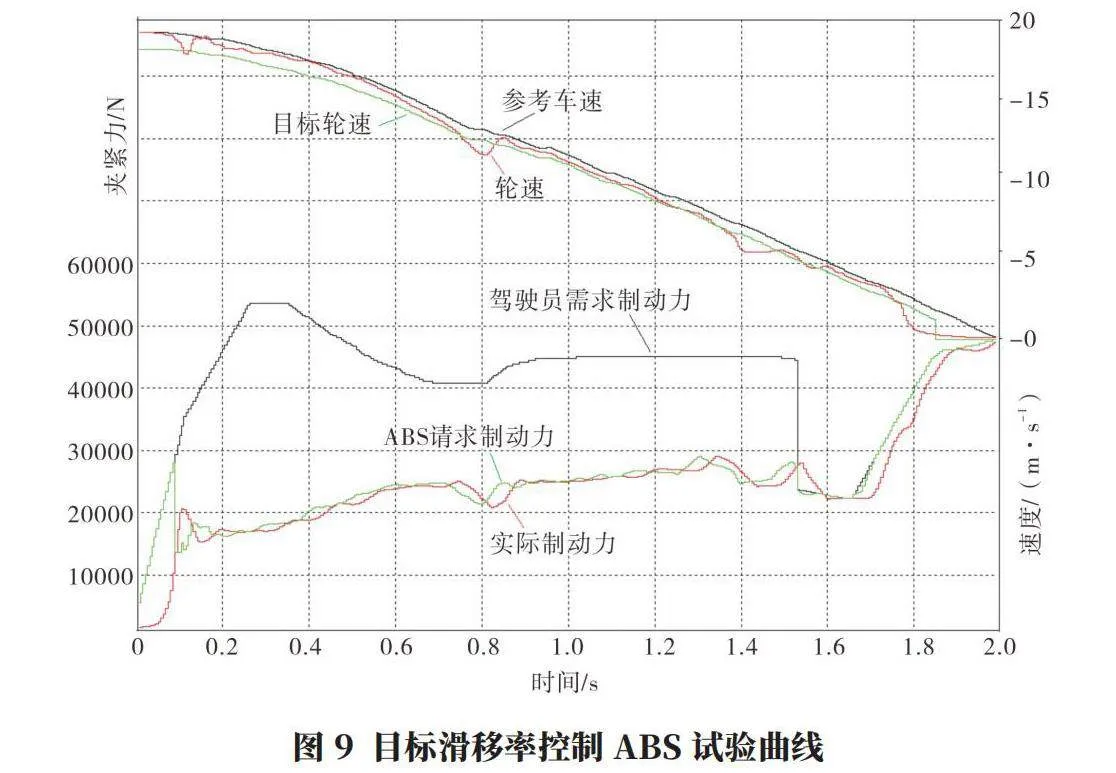
將目標滑移率控制simulink模型生成C代碼，集成到電控制動系統中，并進行實車試驗，試驗曲線如圖9所示。

從試驗曲線可以看出，整個ABS過程中，實際的輪速非常貼合目標輪速，從而可獲得很高的附著系數利用率，整車平均減速度1 g。并且目標滑移率控制的制動力非常平滑（門限值控制制動力波動大），在整個制動過程中，整車減速度波動小于0.1 g（門限值控制0.3 g），主觀感覺極其平順。

4 結語

本文設計了基于目標滑移率控制ABS算法，并與車輛模型進行聯合仿真，最后將ABS控制代碼集成到電控制動系統中進行實車試驗。仿真和試驗結果都表明，基于目標滑移率控制的ABS算法在制動過程中能達到很好的制動效果，在制動安全方面有較突出的優勢。本文研究為目標滑移率控制ABS算法在各種車輛上的廣泛應用打下基礎。

參考文獻：

[1]張新.汽車液壓防抱死制動系統（ABS）的理論與實踐[M].長沙：中南大學出版社，2005.

[2]程軍.汽車防抱死制動系統的理論和實踐[M].北京：北京理工大學出版社，1998.

[3]Zegelaar P W A.The dynamic response of tyres to brake torque variations and road unevenesses[J].Mechanical Maritime & Materials Engineering，1998，25：71-80.

[4]Automotive Anti-Lock Braking System（ABS）Market：2018 Global Industry Size，Share，Growth，Trends Analysis By Sensors，Electronic Control Unit，Hydraulic Unit，and Vehicles Types[M].M2 Presswire，2018.

[5]AAU，VSB.Intelligent anti-lock braking system of electric vehicle with the possibility of mixed braking using fuzzy logic[J].Journal of Physics： Conference Series，2021，11：61-70.

[6]張海濤，盧蕩，肖攀，等.SWIFT與FTire輪胎模型的應用對比[C]//第十四屆中國CAE工程分析技術年會論文集.中國機械工程學會機械工業自動化分會，中國力學學會產學研工作委員會，中國計算機學會高性能計算專業委員會，陜西省國防科技工業信息化協會，2018：205-208.

作者簡介：

張平平，男，1984年生，工程師，研究方向為ABS/ESC控制算法設計。