不同口徑蒸滲儀潛水蒸發差異性研究及模擬

梅海鵬 汪智群 李偉 周超

摘要 為探究不同小口徑蒸滲儀測量潛水蒸發的差異性和隨機森林回歸模型對潛水蒸發的模擬效果，本研究利用五道溝實驗站0.3、0.5 m2蒸滲儀開展了潛水蒸發對比試驗。分析兩種口徑蒸滲儀潛水蒸發量的相關性，并基于隨機森林回歸模型對兩種口徑蒸滲儀潛水蒸發量進行模擬，評估不同氣象要素對潛水蒸發的影響。結果表明，當潛水蒸發量超過2.393 mm時，0.3 m2蒸滲儀測量潛水蒸發量大于0.5 m2蒸滲儀量；0.3 m2蒸滲儀測量潛水蒸發存在遲滯效應。凈輻射對于0.3 m2蒸滲儀潛水蒸發量影響更大，在氣象因素對0.5 m2蒸滲儀潛水蒸發影響中，40 cm土壤含水量的影響更大。空氣濕度、土壤濕度是導致0.3、0.5 m2小口徑蒸滲儀潛水蒸發存在差異的主要因素，可利用隨機森林回歸模型通過氣象要素對潛水蒸發進行預測。

關鍵詞 蒸滲儀；潛水蒸發；口徑；隨機森林回歸模型

中圖分類號 S152.7? ?文獻標識碼 A

文章編號 1007-7731（2024）08-0111-08

Study and simulation of the variability of diving evaporation in different sizes of

evapotranspiration meters

MEI Haipeng1，2? ? WANG Zhiqun3? ? LI Wei3? ? ZHOU Chao1

（1Anhui and Huaihe River Institute of Hydraulic Research（Anhui Provincial Water Conservancy Engineering

Quality Testing Center Station）， Bengbu 233000， China;

2Key Laboratory of Water Conservancy and Water Resources of Anhui Province， Bengbu 233000， China;

3Anhui Huaihe Water Technolgy Co.， Ltd.， Bengbu 233001， China）

Abstract In order to investigate the variability of phreatic evaporation measured by different small-diameter lysimeters and the simulation effect of the random forest regression model on phreatic evaporation， a comparison experiment of phreatic evaporation was carried out by using 0.3 and 0.5 m2 lysimeters in Wudaogou Experimental Station. The correlation of phreatic evaporation of two calibers of evapotranspiration meters was analyzed， and the phreatic evaporation of two calibers of lysimeters was simulated based on the random forest regression model， and the significance of the influence of different meteorological elements on phreatic evaporation was evaluated. The results showed that when the phreatic evaporation exceeds 2.393 mm， the phreatic evaporation measured by 0.3 m2 lysimeter was larger than that by 0.5 m2 lysimeter; there was a hysteresis effect in the diving evaporation measured by 0.3 m2 lysimeter. Net radiation had a greater effect on 0.3 m2 lysimeter phreatic evaporation， and among the effects of meteorological factors on 0.5 m2 lysimeter phreatic evaporation， 40 cm soil water content had a greater effect. Air humidity and soil moisture were the main factors that lead to the difference in phreatic evaporation from 0.3 and 0.5 m2 lysimeters， and the random forest? regression model could be used to predict phreatic evaporation through meteorological factors.

Keywords lysimeter; phreatic evaporation; caliber; random forest regression model

潛水蒸發是地下水損失的主要途徑之一[1]，該過程易受到土壤蒸發、植物蒸騰等多種因素影響[2]。無效的潛水蒸發可能導致部分地下水損失，影響農業土壤水分利用、土壤鹽分分布[3]等。長期以來，許多水文水資源[4]、生態環境[5-6]和農業水土[7-8]等領域的學者利用蒸滲儀開展了大量關于潛水蒸發的研究。這些用于試驗研究的蒸滲儀規格多樣，不同口徑的蒸滲儀在潛水蒸發測量上存在差異[9-10]。在水面蒸發、蒸散發方面，已有許多學者對不同口徑蒸滲儀測量結果的差異性進行分析[11-12]，而對不同口徑蒸滲儀測量的潛水蒸發量存在差異的機理研究較少。本文基于五道溝實驗站地中蒸滲儀設備，研究在裸土情況下0.3、0.5 m2兩種口徑蒸滲儀在潛水蒸發測量上的表現，探索兩種口徑蒸滲儀的潛水蒸發測量差異，并對產生差異的機理進行分析，為區域潛水蒸發觀測和農田水分管理提供參考。

1 材料與方法

1.1 試驗區基本情況

該試驗于2018—2020年在五道溝水文水資源實驗站大型地中蒸滲儀試驗場進行，實驗站位于淮河中游區，淮北平原南部，屬于北亞熱帶濕潤季風氣候與南溫帶半濕潤季風氣候區的過渡帶，季風顯著，四季分明。該區域土壤類型主要為砂姜黑土，土壤平均干容重1.36 g/cm3，滲透系數24.2 mm/h。實驗站內設有標準氣象場及高精度氣象站，可進行氣溫、降水、蒸發、風速和輻射等多種水文氣象要素觀測。

1.2 試驗設計

選取面積為0.3和0.5 m2的蒸滲儀測筒，編號分別為L0.3和L0.5。為保障潛水蒸發順利進行，地下水埋深均設置為0.2 m，由馬氏瓶裝置控制，測筒內土壤均為當地砂姜黑土原狀土。蒸滲儀測筒與觀測室內補水裝置馬氏瓶連接，每日8：00讀取馬氏瓶水位，并將當日數據與前一日數據差值作為前一日潛水蒸發量，分辨率0.1 mm。試驗選取的蒸滲儀裝置見圖1。

1.3 數據測量與處理

1.3.1 潛水蒸發數據系列? 為探究兩種口徑蒸滲儀潛水蒸發測量的年內差異，根據當地作物生育期將各年度潛水蒸發數據系列劃分為小麥同期和玉米同期兩組。為避免冬季土壤凍融[13]對潛水蒸發觀測產生影響，各年度小麥同期潛水蒸發數據選取當年2月至收割期間的數據，玉米同期為整個生育期數據系列。根據白鵬等[14]的研究，降水會對蒸散發產生影響，因此剔除雨期和蒸滲儀測筒內產生入滲水量時期的數據。2018—2020年度各組潛水蒸發數據選取時段及有效數據天數見表1。

1.3.2 水文氣象因子? 本文通過對17種水文氣象因子進行判別，分析不同水文氣象要素對不同口徑蒸滲儀潛水蒸發量的影響程度。試驗所選取的有效數據日同期氣象要素由距地中蒸滲儀實驗場30 m處的標準氣象場和高精度氣象站測量。其中，標準氣象場測量每日水面蒸發數據（E601B）、最高溫度（Tmax）、最低溫度（LT）、日照時數（SUN）、相對濕度（RH）、水汽壓力差（VPD）、露點溫度（DT）、地表溫度（LST）和梯度土壤溫度（ST20、ST40）等要素。高精度氣象站測量空氣濕度（H）、凈輻射（NR）、梯度土壤濕度（SH20、SH30和SH40）、風速（WS）和日均氣溫（MT）等要素，頻次為10 min/次，采用日均值。

1.4 隨機森林回歸模型預測

基于隨機森林回歸模型[15]（RF）對蒸滲儀潛水蒸發量進行預測，并評估輸入參數氣象要素對潛水蒸發影響的重要性。RF是以決策樹之分類回歸樹（CART）為基礎構建的一種集成學習模型，該模型只須調整ntree、mtry等較少的自定義參數就能完成模型的構建。隨機森林由多棵弱決策樹組成，能更好地防止過擬合現象，且具備處理大量數據集、給出輸入變量重要性評估和排序等優點[16]。以RF模型節點純度增加值作為變量重要性評估指標，具體操作方法：在RF模型各決策樹節點加入隨機值，通過判定隨機值導致模型袋外數據誤差[17]升高的幅度來確定變量的重要程度。誤差變化幅度越大，該變量對模型的重要程度越高，反之則變量重要程度越低。其計算如式（1）所示。

[INPi=（EOOB2 ?EOOB1 ）ntree] （1）

式中，[INPi]為變量i的重要性；[EOOB1 ]為袋外數據誤差；[EOOB2 ]為袋外數據所有樣本i加入隨機值變化，再次計算的袋外誤差。

利用Matlab（2016 b）構建RF模型，設置模型中參數ntree=100，mtry=3，選擇80%樣本量作為訓練集，剩余20%作為測試集。采用隨機亂序方式劃分訓練集和測試集樣本，采用納什效率系數NSE對RF模型性能進行評估，采用均方根誤差RMSE、平均絕對誤差MAE對RF模型精度進行評價。

2 結果與分析

2.1 不同口徑蒸滲儀潛水蒸發差異性分析

將試驗期內各年度L0.3、L0.5測筒潛水蒸發數據參考當地典型作物種植周期分為冬小麥同期、夏玉米同期和全年3組數據進行分析比較。由圖2（A）和表2可知，2018年L0.3與L0.5的R2為0.703，其中冬小麥同期為0.779、夏玉米同期為0.576，冬小麥期L0.3與L0.5潛水蒸發量相關性最強，夏玉米期最差。3組潛水蒸發量關系趨勢線斜率均小于1，其中冬小麥同期>全年>夏玉米同期，冬小麥同期與全年潛水蒸發量關系趨勢更為接近。L0.3與L0.5關系趨勢線斜率小于1，表明L0.5在潛水蒸發量較小時高于L0.3潛水蒸發量，蒸滲儀潛水蒸發量較大時L0.5小于L0.3。3組關系線與1∶1線交點均接近，橫坐標在3.799～3.857 mm，按照2018年測筒L0.3與L0.5潛水蒸發量關系趨勢線與1∶1線的交點（3.857，3.857），可以認為在日潛水蒸發量超過3.827 mm時，L0.3與L0.5所測潛水蒸發量大小關系發生改變。以趨勢線截距作為潛水蒸發產生閾值，可知L0.5先于L0.3產生潛水蒸發。對于2018年，當L0.5每天平均所測潛水蒸發量達到0.722 mm時，L0.3才開始觀測到潛水蒸發。由圖2（B）和表2可知，2019年L0.3與L0.5的R2為0.326，其中冬小麥同期為0.497、夏玉米同期為0.522，各組潛水蒸發量相關性均很差。3組潛水蒸發量關系趨勢線斜率均小于1，其中全年>夏玉米同期>冬小麥同期，夏玉米同期與全年潛水蒸發量關系趨勢線斜率更為接近。夏玉米同期相關趨勢線與1∶1線交點較大，為（3.008，3.008），冬小麥同期相關趨勢線與1∶1線交點與全年較為接近，橫坐標為0.832 mm。按照2019年測筒L0.3與L0.5潛水蒸發量關系趨勢線與1∶1線的交點（0.849，0.849），可以得出，在日潛水蒸發量超過0.849 mm時，L0.3與L0.5所測潛水蒸發量大小關系發生改變。按照線性趨勢線截距可知，2019年，當L0.5日潛水蒸發量達到0.241 mm時，L0.3才開始觀測到潛水蒸發。由圖2（C）和表2可知，2020年L0.3與L0.5的R2為0.736，其中冬小麥同期為0.857、夏玉米同期為0.501。3組潛水蒸發量關系趨勢線斜率同樣均小于1，其中全年>冬小麥同期>夏玉米同期，全年潛水蒸發量關系趨勢線基本與1∶1線一致。各組趨勢線與1∶1線交點差距較大，橫坐標在1.913～5.654 mm，冬小麥同期最小，全年最大。按照2020年L0.3與L0.5潛水蒸發量關系趨勢線與1∶1線的交點（5.654，5.654）可知，在日潛水蒸發量超過5.654 mm時，L0.3與L0.5所測潛水蒸發量大小關系才發生改變。根據趨勢線截距可知，2019年當L0.5日潛水蒸發量達到0.278 mm時，L0.3才開始觀測到潛水蒸發數據。由圖2（D）可知，通過對各年度有效數據天數的累積蒸發量進行分析發現，2018年和2020年L0.3與L0.5的累積潛水蒸發量與1∶1線接近，2019年明顯低于1∶1線。根據圖2（D）可知，通過對2018—2020年間L0.3與L0.5的5日累積潛水蒸發關系分析可知，各年度L0.3與L0.5所測潛水蒸發量相關性達0.980以上。2018、2020年累積關系趨勢線斜率分別為0.992、1.091，與1∶1線基本一致，2019年累積關系趨勢線斜率為0.799。2018年和2020年L0.3與L0.5所測潛水蒸發量累積關系更為接近，其中2020年表現出L0.5略高于L0.3，2019年則表現出L0.3累積潛水蒸發量高于L0.5。

L、LW和LC分別表示整個時期、冬小麥同期和夏玉米同期無作物測筒潛水蒸發量，0.3、0.5表示相應測筒面積為0.3 m2、0.5 m2；L2018-0.3、L2018-0.5分別表示2018年0.3、0.5 m2無作物測筒潛水蒸發量。其余年份以此類推。（A）2018年，（B）2019年，（C）2020年，（D）2018—2020年累積。

通過對各年度L0.3與L0.5日潛水蒸發量相關關系分析發現，兩種口徑蒸滲儀潛水蒸發量關系規律存在一定的年際差異，而在同一年度，根據作物種植周期劃分的冬小麥同期、夏玉米同期和全年潛水蒸發系列也存在一定的差異。其中2018年與2020年規律基本一致，主要為2019年存在差異。2018、2020年L0.3與L0.5潛水蒸發量關系的R2大小關系為冬小麥同期>全年>夏玉米同期，2019年則是夏玉米同期>冬小麥同期>全年。在2018、2020年冬小麥同期和全年的R2在0.703～0.857，而夏玉米同期的R2只有0.576、0.501，相關性不高；2019年各組潛水蒸發系列的R2僅在0.326～0.522，以夏玉米同期最高。2018、2020年L0.3與L0.5線性趨勢線斜率大小關系與R2關系一致，而2019年則表現出全年>夏玉米同期>冬小麥同期。2018、2020年L0.3與L0.5與1∶1線交點橫坐標均為全年>夏玉米同期>冬小麥同期，全年與夏玉米同期更接近；而2019年夏玉米同期>全年>冬小麥同期，全年與冬小麥同期更接近。各年度L0.3與L0.5測潛水蒸發累積量相關關系方面，各年度R2均超過0.980，但2018、2020年累積關系趨勢線斜率更接近1，而2019年累積關系趨勢線斜率為0.799。可以看出，在2019年存在影響因素對這兩種尺寸蒸滲儀的潛水蒸發測量產生影響。根據3年的L0.3與L0.5潛水蒸發量線性關系參數平均值建立0.3和0.5 m2蒸滲儀日潛水蒸發關系，如式（2）所示。

[L0.5=0.827 L0.3+0.414] （2）

計算結果表明，日潛水蒸發量平均超過2.393 mm時，L0.3與L0.5所測潛水蒸發量大小關系才發生改變；當L0.5日潛水蒸發量平均達到0.414 mm時，L0.3才開始觀測到潛水蒸發數據。

利用箱型圖對L0.3與L0.5比值分布范圍進行統計分析如圖3所示。圖3（A）中2018年與2020年日潛水蒸發量比值數據相比2019年更集中，但存在異常值，而2019年更離散。2018、2019和2020年比值中位數分別為1.000、1.233和0.951，2018年和2020年中位數更加接近。根據圖3（B）對累積潛水蒸發量比值分布分析發現，2018、2020年比2019年更集中，但存在異常值，其中2018年為偏大異常值，說明L0.3比L0.5潛水蒸發量數據更大，2020年為偏小異常值，說明L0.3比L0.5潛水蒸發量數據更小。2018、2019年和2020年比值中位數分別為0.993、1.083和0.969，中位數值更加接近，但2019年數據離散程度更大。

2.2 基于隨機森林回歸模型的潛水蒸發模擬

根據2018—2020年有效潛水蒸發量數據，按照8∶2隨機劃分訓練集和測試集數據，用于構建模型并對其進行評價。分別以L0.3、L0.5潛水蒸發量以及L0.3與L0.5比值作為輸出變量，以相應的17種氣象因子作為特征變量構建RF模型。由表3可知，在測試集模型評價指標中，各模型的質量和預測效果相比訓練集均有所下降，考慮是隨機森林回歸模型在進行訓練集數據范圍以外的預測時，可能存在一些未考慮到的影響要素和噪聲較大的樣本導致預測誤差出現。測試集RFL0.3與RFL0.5的NSE相差不大，分別為0.679、0.665，表明構建的模型質量基本相同。RFL0.3的RMSE和MAE均大于RFL0.5，分別高0.020、0.019 mm，表明對0.3 m2測筒潛水蒸發模擬的誤差要大于0.5 m2測筒，相比于0.5 m2蒸滲儀，對0.3 m2測筒的潛水蒸發量模擬有更多的不確定因素。對二者的比值模擬中，RFL0.3/0.5模型有較高的質量，NSE達到0.708，RMSE和MAE均較小，分別為0.207、0.146。由圖4可知，基于各RF模型計算的0.3、0.5 m2蒸滲儀潛水蒸發量預測值與實測值關系，R2分別為0.726和0.671，利用RF模型對0.3 m2蒸滲儀潛水蒸發量的預測值與真實值有更好的相關關系。

2.3 氣象因子重要性評估

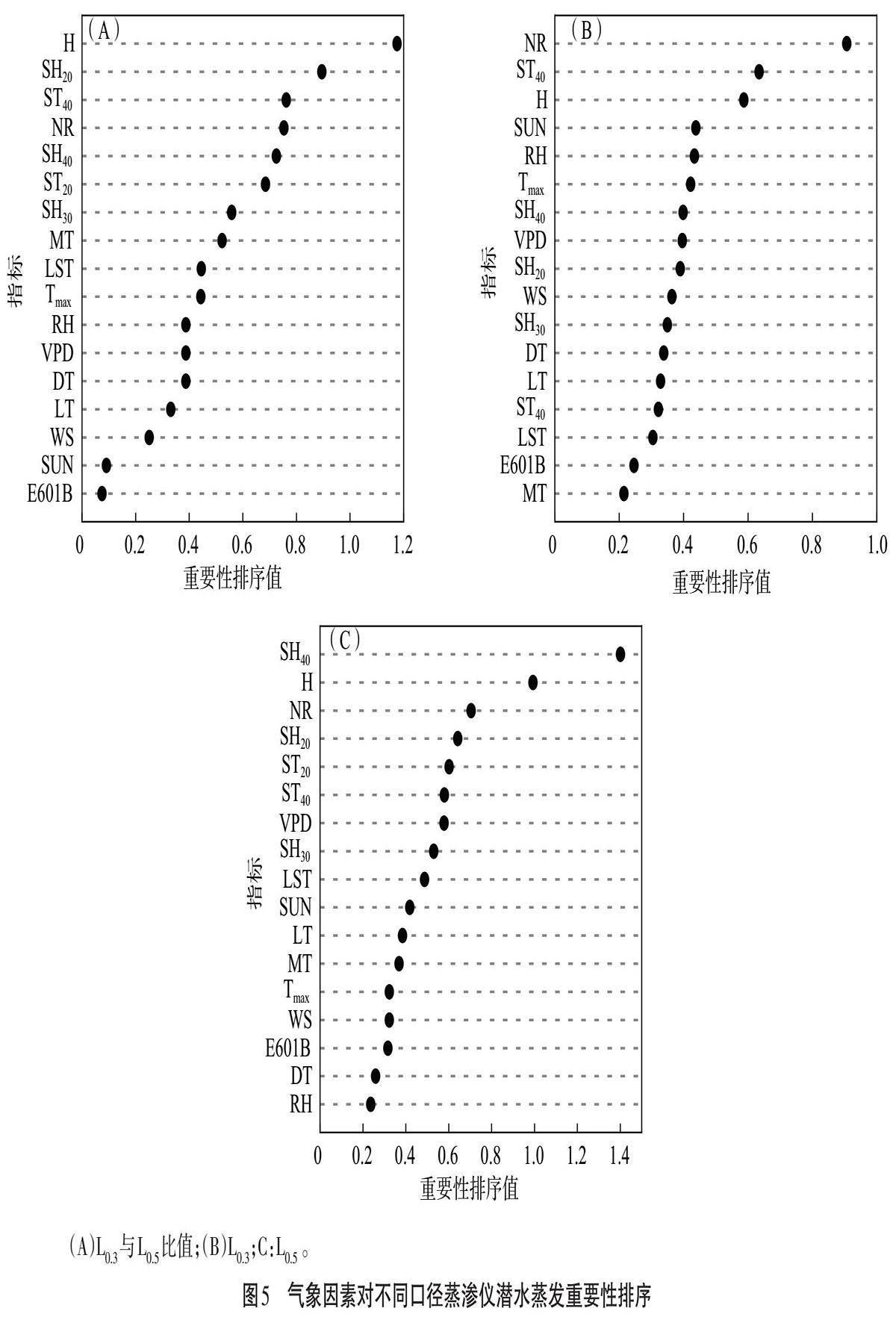
基于RF模型對不同氣象因子在預測潛水蒸發量時的重要性排序如圖5所示。影響0.3 m2蒸滲儀潛水蒸發量主要為NR、ST40和H，影響0.5 m2蒸滲儀潛水蒸發量主要為SH40、H和NR。根據影響因子重要性排序值可知，當測筒面積由0.3 m2擴大到0.5 m2時，SH40相比NR和ST40對潛水蒸發的影響更大。氣象因子中SH40指標為氣象觀測場內土壤含水量指標，根據相關研究，太陽輻射對土壤含水量有著顯著影響[18]。太陽輻射使得土壤產生梯度溫度，進而驅動潛水蒸發改變土壤含水量，因此SH40指標一定程度上反映了太陽輻射對田間潛水蒸發的驅動能力，這與蒸滲儀測筒面積越大越接近大田潛水蒸發情況一致。在氣象因子對L0.3和L0.5比值的影響中，以H、SH20和ST40更為重要，表明空氣濕度、土壤濕度和土壤溫度是導致0.3、0.5 m2蒸滲儀潛水蒸發存在差異的重要因素。

3 結論與討論

（1）0.3與0.5 m2蒸滲儀在潛水蒸發測量上存在差異，當兩種蒸滲儀所測日潛水蒸發關系在潛水蒸發量達到2.393 mm時，0.3 m2蒸滲儀測量潛水蒸發量由小于0.5 m2蒸滲儀量變為大于。在不同尺寸蒸滲儀測筒導致的潛水蒸發遲滯效應影響下，當0.5 m2所測蒸滲儀潛水蒸發量平均達到0.414 mm時，0.3 m2蒸滲儀才開始出現潛水蒸發，這種誤差會隨著連續多日的潛水蒸發測量而減小，不會影響兩種尺寸蒸滲儀在長系列累積蒸發量測量中的精度。

（2）NR、SH40分別是影響0.3、0.5 m2蒸滲儀潛水蒸發的重要因素，空氣濕度和土壤濕度是導致0.3和0.5 m2蒸滲儀潛水蒸發差異存在的主要因素。基于RF模型，利用氣象要素對潛水蒸發預測具有較高的精度，可作為潛水蒸發的預測工具。

利用蒸滲儀法進行潛水蒸發量測量，具有準確、方便等特點。本文通過對連續3年內兩種口徑蒸滲儀測量潛水蒸發進行比較分析，發現當日潛水蒸發超過2.393 mm時，0.3 m2蒸滲儀測量潛水蒸發量由小于0.5 m2蒸滲儀量變為大于。考慮可能是由于蒸滲儀測筒材料為鐵，當日潛水蒸發超過一定量時，當日氣溫及輻射較高，而土壤與鐵的比熱容存在差異，導致0.3 m2蒸滲儀測筒受到的邊緣效應強于0.5 m2蒸滲儀測筒，導致0.3 m2蒸滲儀測筒潛水蒸發量更大。這與上述結果得出的NR對0.3 m2蒸滲儀測筒的影響更大表現一致。當0.5 m2蒸滲儀平均測量到0.414 mm日蒸發時，0.3 m2蒸滲儀才開始出現潛水蒸發，這可能與蒸滲儀測筒面積與馬氏瓶直徑大小有關。當0.3與0.5 m2蒸滲儀產生同樣的潛水蒸發量時，由于為兩種尺寸蒸滲儀測筒補水的馬氏瓶規格一致，0.5 m2蒸滲儀對應的馬氏瓶補水量更多，水面差更大，而根據圖1（D）中兩種尺寸蒸滲儀累積蒸發量關系可知，這種日潛水蒸發測量誤差在多日累積潛水蒸發中會被降低。

通過隨機森林回歸模型對17種氣象因子對潛水蒸發影響的重要程度進行評估。結果可知，NR對0.3、0.5 m2蒸滲儀潛水蒸發量影響重要性均靠前，太陽凈輻射是驅動潛水蒸發的主要因素之一。在0.5 m2蒸滲儀潛水蒸發量影響因素中，以SH40最重要，其次為H和NR。徐飛等[19]研究認為，土壤梯度溫度是影響潛水蒸發的重要因素，與本研究結果一致。氣象因素對兩種口徑蒸滲儀潛水蒸發比值的影響中，主要因素為空氣濕度或土壤濕度，這與孫曉旭等[20]得出的空氣濕度、土壤含水率對潛水蒸發影響規律一致。

綜上，本文利用五道溝實驗站0.3、0.5 m2蒸滲儀開展了潛水蒸發對比試驗，分析兩種口徑蒸滲儀潛水蒸發量的相關性，并基于隨機森林回歸模型對兩種口徑蒸滲儀潛水蒸發量進行模擬，評估不同氣象要素對潛水蒸發影響的重要程度。結果表明，當潛水蒸發量超過2.393 mm時，0.3 m2蒸滲儀測量潛水蒸發量將大于0.5 m2蒸滲儀量；0.3 m2蒸滲儀測量潛水蒸發存在遲滯效應。凈輻射對于0.3 m2蒸滲儀潛水蒸發量影響更大，在氣象因素對0.5 m2蒸滲儀潛水蒸發影響中，40 cm土壤含水量的影響更大。空氣濕度、土壤濕度是導致0.3、0.5 m2蒸滲儀潛水蒸發存在差異的主要因素，可利用隨機森林回歸模型通過氣象要素對潛水蒸發進行預測。

參考文獻

[1] 劉佩貴，夏艷，尚熳廷. 不同質地裸土潛水蒸發估算方法[J]. 農業工程學報，2020，36（1）：148-153.

[2] 郭占榮，荊恩春，聶振龍，等. 種植條件下潛水入滲和蒸發機制研究[J]. 水文地質工程地質，2002，29（2）：42-44，68.

[3] 賈瑞亮，周金龍，周殷竹，等. 干旱區高鹽度潛水蒸發條件下土壤積鹽規律分析[J]. 水利學報，2016，47（2）：150-157.

[4] 張志山，趙洋，張亞峰，等. 中國北方沙區水量平衡自動模擬監測系統（沙坡頭蒸滲儀群）[J]. 中國科學院院刊，2021，36（6）：733-743，755.

[5] 魏寧寧，母艷梅，姜曉燕，等. 毛烏素沙地油蒿-楊柴灌叢生態系統蒸散組分分配及其影響因子[J]. 應用生態學報，2021，32（7）：2407-2414.

[6] 張夢迪，張立鋒，陳之光，等. 土壤蒸發和植被蒸騰對三江源退化高寒草甸蒸散的影響[J]. 生態學報，2021，41（18）：7138-7152.

[7] 穆家偉，查天山，賈昕，等. 毛烏素沙地典型沙生灌木對土壤蒸發的影響[J]. 北京林業大學學報，2016，38（12）：39-45.

[8] 賈劍波，余新曉，王賀年，等. 暴雨條件下北京山區主要喬木蓄水能力研究[J]. 水土保持通報，2013，33（3）：114-117.

[9] 楊炳玉，申雙和，張富存，等. 不同尺寸蒸滲儀測定作物蒸散的田間試驗研究[J]. 中國農業氣象，2015，36（2）：161-169.

[10] 劉春偉，邱讓建，孫亞卿，等. 不同材料和尺寸微型蒸滲儀測定土壤蒸發量[J]. 中國農村水利水電，2018（6）：1-5.

[11] 劉紅霞，王飛，黃玲，等. 烏蘇E-601B型蒸發與小型蒸發折算系數分析[J]. 沙漠與綠洲氣象，2012，6（6）：65-68.

[12] 王永亮，張學知，喬光建. 河北省平原區20 m2水面蒸發池與不同型號蒸發器折算系數分析[J]. 水文，2012，32（4）：58-62.

[13] 王振龍，楊秒，呂海深，等. 基于蒸滲儀群淮北平原凍融期裸土及麥田潛水蒸發規律研究[J]. 農業工程學報，2019，35（13）：129-137.

[14] 白鵬，蔡常鑫. 1982—2019年中國陸地蒸散發變化的歸因分析[J]. 地理學報，2023，78（11）：2750-2762.

[15] BREIMAN L.Random forests[J].Machine language，2001，45（1）：5-32.

[16] 王茵茵，齊雁冰，陳洋，等. 基于多分辨率遙感數據與隨機森林算法的土壤有機質預測研究[J]. 土壤學報，2016，53（2）：342-354.

[17] MART?NEZ-MU?OZ G，SU?REZ A.Out-of-bag estimation of the optimal sample size in bagging[J].Pattern recognition，2010，43（1）：143-152.

[18] 李含雪. 基于氣象數據和機器學習的土壤溫度和水分預測模型構建[D]. 哈爾濱：東北農業大學，2022.

[19] 徐飛，史文娟，邢旭光，等. 覆膜開孔條件下新疆地區潛水蒸發及水熱關系研究[J]. 西北農林科技大學學報（自然科學版），2013，41（10）：172-178.

[20] 孫曉旭，王開材，丁克強. 潛水蒸發特征試驗研究[J]. 人民黃河，2015，37（3）：62-64，71.

（責編：楊 歡）

基金項目 水利部重大科技項目（SKS-2022066）。

作者簡介 梅海鵬（1996—），男，安徽蚌埠人，碩士，助理工程師，從事水文水資源研究。

通信作者 汪智群（1990—），女，安徽池州人，工程師，從事水文水資源研究。

收稿日期 2024-01-26