質量體積雙約束下車輛裝載與配送路徑聯合優化研究

任宗偉，錢志軍，鄭瑋，蒲煒，張寧，祁彬彬

質量體積雙約束下車輛裝載與配送路徑聯合優化研究

任宗偉1*，錢志軍2，鄭瑋2，蒲煒3，張寧3，祁彬彬2

（1.哈爾濱商業大學 管理學院，哈爾濱 150028；2.昆侖數智科技有限責任公司，北京 100000； 3.中國石油天然氣股份有限公司河北銷售分公司，石家莊 050000）

針對質量與體積共同限制的配送路徑問題，綜合考慮訂單不可拆分、貨物的體積等約束，構建包含路徑最短和裝載率最高雙目標的車輛裝載與配送路徑聯合優化模型。在車輛路徑優化模型的求解方面，首先利用聚類算法對配送區域進行劃分，然后通過車輛的載質量判斷是否能進行站點貨物的配送，最后利用遺傳算法求得最優路徑。在三維裝載模型的求解上使用貪心算法和基于塊的啟發式算法，解決了貨物的裝箱問題。基于某公司具體實例對模型與算法的可行性進行了驗證，優化后配送的車輛減少了1輛，配送距離減少了154.247 km，平均裝載率達到了93.89%，節省了企業的配送成本。所構建的模型以及求解的算法可以提高裝載率和配送效率，為解決車輛裝載與配送路徑聯合優化問題提供理論依據。

路徑優化；遺傳算法；三維裝載；基于塊的啟發式算法

根據2022年的最新通報，我國物流受疫情影響態勢逐漸減小，現已逐漸恢復，社會物流逐漸增長。其中在運輸方面為9.55萬億元，由此可見運輸在人們的日常生活中占有很大的比重。隨著經濟的快速發展，配送占領著重要的地位，在配送形式、配送路徑、配送時間等方面都要進行具體合理的安排與規劃。但大多數的企業或物流公司尚未形成完整的配送體系，運輸、倉儲、銷售等都存在極大的問題，深深地影響著企業的發展。想要降低企業的運輸成本，促進企業的發展，其中一個重要的措施是合理規劃配送路徑和車輛裝載。現大多數企業在配送貨物時僅僅依靠人為經驗和貨物的緊急程度進行配送，效率較低，如出現緊急情況也無法有效調動機動人員和車輛，經常容易出現紕漏，需要花費較多的人力成本和時間成本。現階段考慮路徑優化時同時考慮裝箱問題的情況較少，如何在滿足盡可能多的裝箱基礎上優化配送路徑，仍然是值得研究的現實問題。

車輛路徑問題（Vehicle Routing Problem，VRP）由Dantzig等[1]于1959年首次提出，現已成為運籌學中一類經典的組合優化問題。隨著實際需求的不斷變化，各種各樣的VRP一直在出現，并不斷地發展。Agárdi等[2]提出了一種通用的VRP模型，并通過案例加以證明。在解決VRP問題時，Joanna等和Olaniyi等[3-4]討論了遺傳算法解決VRP問題。容量約束的車輛路徑問題（Capacitated Vehicle Routing Problem，CVRP）是車輛路徑問題的拓展問題[5]，針對CVRP問題，Simensen等[6]提出了一種混合元啟發式算法解決CVRP問題。梁彪等[7]提出了“一種求解CVRP問題的遺傳蟻群融合算法”，為解決帶容量約束的車輛路徑優化問題提供了一種解決辦法。針對大規模的多倉庫多車型車輛路徑問題（Multi-Depot Heterogeneous Fleet Vehicle Routing Problem，MDHFVRP），多數研究采取先聚類再優化的求解思路，此種方法可以縮小問題規模和降低求解難度。例如，Thangiah等[8]利用遺傳算法進行客戶分群，將問題轉變為旅行商問題，然后通過插入啟發式算法求解旅行商問題。Luo等[9]則改進了蛙跳算法，對客戶聚類后再進行優化，然后對總體進行調整以生成新的聚類，直到滿足設定的收斂標準為止，該方法被證明可以用來求解大規模的多車場車輛路徑問題。

針對三維裝載問題，王超等[10]提出三維裝載與CVRP聯合多目標優化問題（3LCVRPMO）模型，該模型在三維裝載約束下，CVRP問題（3LCVRP）的基礎上，考慮了配送車輛數目及路徑總距離2個目標函數，在權衡裝箱和路徑優化2個優化過程的基礎上，構建了多階段/兩層混合算法架構（MSOTLH）及其算法，并對路徑優化偏好的3LCVRPMO問題進行求解。那日薩等[11]針對7種現實約束的集裝箱三維多箱異構貨物裝載優化問題，提出了一種基于“塊”和“空間”的啟發式搜索算法，并基于Net平臺開發了一款3D裝箱布局優化可視化軟件，已在相關物流企業中得到推廣應用，驗證了算法的實用性。多數學者通過先聚類后裝載來提升車輛的裝載率[12-13]，為三維裝載約束下的路徑優化提供了決策參考和方法支持。王勇等[14]設計了集成k-means時空聚類的Clarke-Wright-非支配排序遺傳算法，為求解三維裝載路徑優化問題提供了方法。崔會芬等[15]探討了三維裝箱約束下的車輛路徑優化問題，引入多種約束，采用遺傳算法進行求解，提高了物流配送效率，降低了配送成本。

本文在車輛路徑優化模型的基礎上增加三維裝載約束限制，考慮帶三維裝載的路徑優化模型，建立質量體積雙約束的路徑優化模型以及車輛的三維裝載模型，并結合具體實例對模型和算法的可行性進行分析。利用聚類算法對站點進行分區，在遺傳算法求解過程中調用求解三維裝載的貪心算法和基于塊的啟發式算法，統籌進行三維裝載和規劃路徑。

1 問題描述

首先已知配送中心和各個配送站點的位置信息、各個站點的需求量信息，其中配送中心有一定數量的車可用于配送，同時配送中心只有一種車型用于配送；已知車輛的載質量和容量，在配送過程中每個車次所走路線裝載的貨物總質量不能超過車的最大載質量，同時每個車次所走路線裝載的貨物總體積不超過車輛容積，每個站點只被服務一次，在某一時刻所有負責配送的車同時從配送中心出發，分別完成各自配送任務之后回到配送中心。在車輛的裝箱問題上要求把一定數量的貨物放入車廂中，使得每個車廂中的貨物體積之和不超過車輛容量，并使車輛數量最少。基于以上條件，設計一個最優的方案，使得車輛配送總路線最短（如圖1所示）。針對該問題，建立了路徑優化模型和三維裝載模型，路徑優化模型的目標函數為車輛行駛的總距離最短，約束條件在經典VRP問題的基礎上添加車載質量約束和容量約束。三維裝載模型為個直方體貨箱在不相互干涉的情況下盡可能多地裝入貨車車廂內，使貨車車廂的空間裝載率最高。將三維裝載模型與路徑優化模型相融合，即在滿足裝箱約束的前提下，盡可能使車輛裝更多的站點的貨物，使配送車輛的總行駛距離最短，具體描述見圖2。

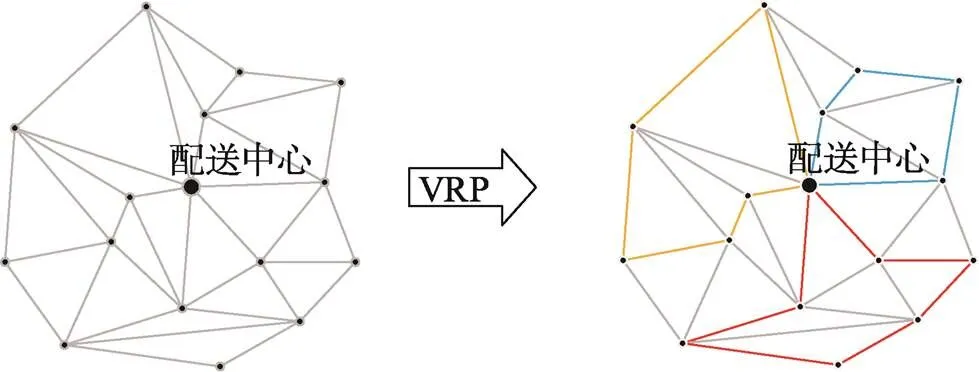
圖1 車輛配送路徑問題描述

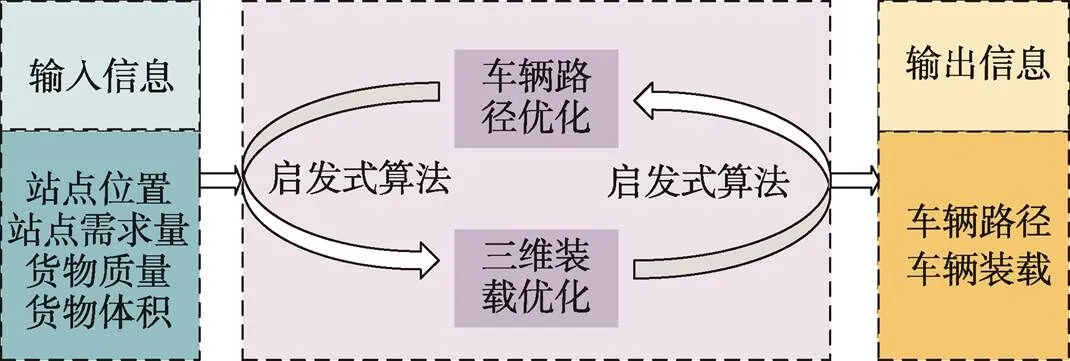
圖2 車輛路徑優化與三維裝載相融合描述

2 數學模型的構建

2.1 模型假設

根據現有條件，本文構建的模型做出以下假設：

假設1：配送中心庫存量可滿足所有客戶需求，且僅有一個配送中心。

假設2：配送中心只有一種車型的車，車輛數足夠完成配送任務。

假設3：車輛從配送中心出發，完成配送任務后再返回配送中心。

假設4：客戶的需求不可分割，每個客戶只能被一輛車服務，且只能被服務一次。

假設5：所有的客戶位置已知，車輛都可以配送到。

假設6：配送車輛只承擔送貨任務，不承擔取貨，配送完成后車輛返回配送中心。

假設7：配送車輛在路上不存在交通擁堵情況。

假設8：所有車輛的實際載重不能超過其額定載重。

假設9：所有車輛的實際載貨體積不能超過其額定容積。

假設10：客戶需求是靜態的，確定后將不會發生改變。

假設11：不考慮單個客戶的需求量多于一輛車的最大載質量的情況。

假設12：不考慮單個客戶的需求貨物體積大于一輛車的最大容積的情況。

假設13：貨物都是規則物體。

假設14：貨箱必須放置在車廂內部，不能夠超出車輛的邊界范圍。

假設15：貨箱的長寬高和質量信息都是已知的。

假設16：實際裝載過程中貨箱與貨箱之間的裝載間隙忽略或者可以看作車廂在計算空間的時候已經預留一部分作為裝載間隙。

假設17：貨箱不會由于堆積而產生變形，不是危險品等特殊貨物。

2.2 參數說明

本文建立的模型中所有參數說明如下。

2.3 模型的構建

2.3.1 路徑優化模型

數學模型建立如下：

目標函數：

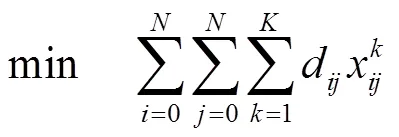
約束條件：

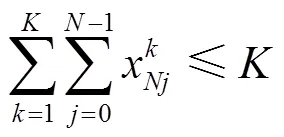
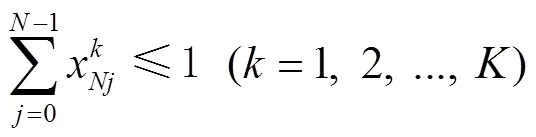
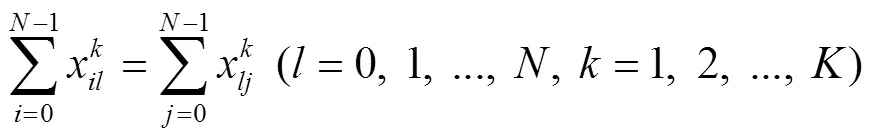
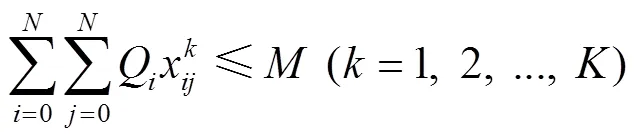
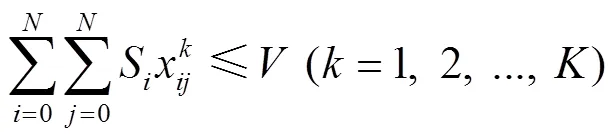
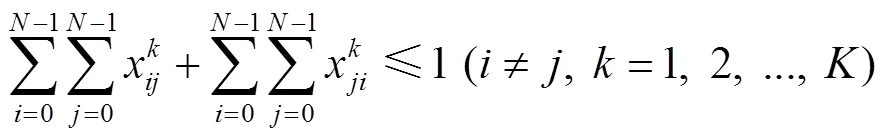
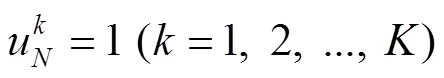
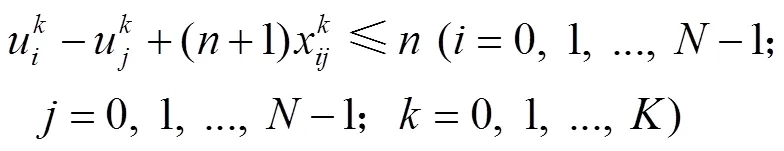
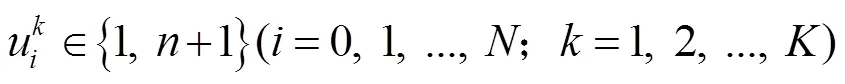
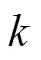
2.3.2 三維裝載模型

數學模型建立如下。

目標函數：

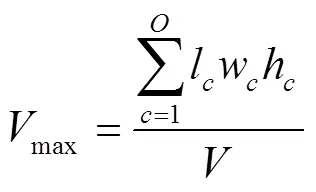
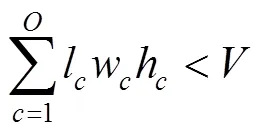
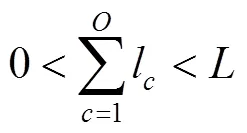
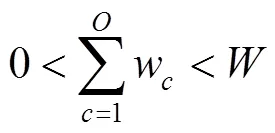
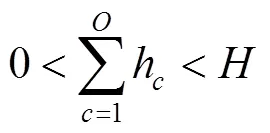
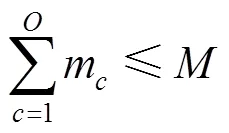
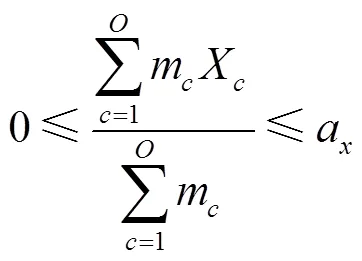
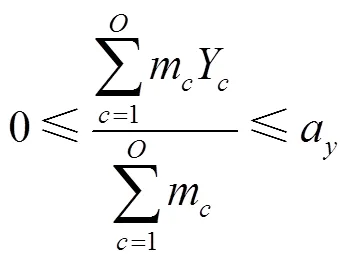
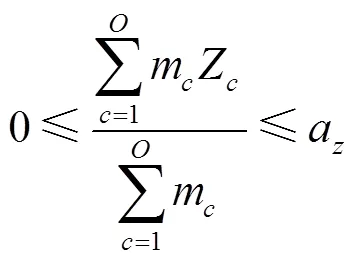
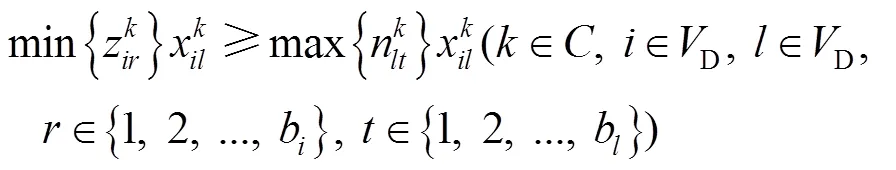
式（12）為車廂體積利用率最優，即在貨車車廂中對要裝入的貨箱1,2,3, ...,P尋找一個合適的貨物裝載順序，使得裝入的貨箱體積最大，車廂的剩余空間最小；式（13）表示貨箱總體積約束；式（14）、式（15）、式（16）表示貨箱三維尺寸長寬高約束；式（17）表示貨物總質量約束；式（18）、式（19）、式（20）表示集裝箱裝滿貨物后的重心范圍約束；式（21）表示貨物 “先進后出”的約束。

3 算法實現

在總體方案設計按照車輛路徑優化和三維裝載優化2個任務開展研究。車輛路徑優化方面，在考慮車型種類、商品質量和體積的基礎之上構建優化模型；在三維裝載優化中主要考慮的因素包括配送順序、體積、三維旋轉、質量等。2個任務的求解算法以元啟發式算法為主。框架如圖3所示。

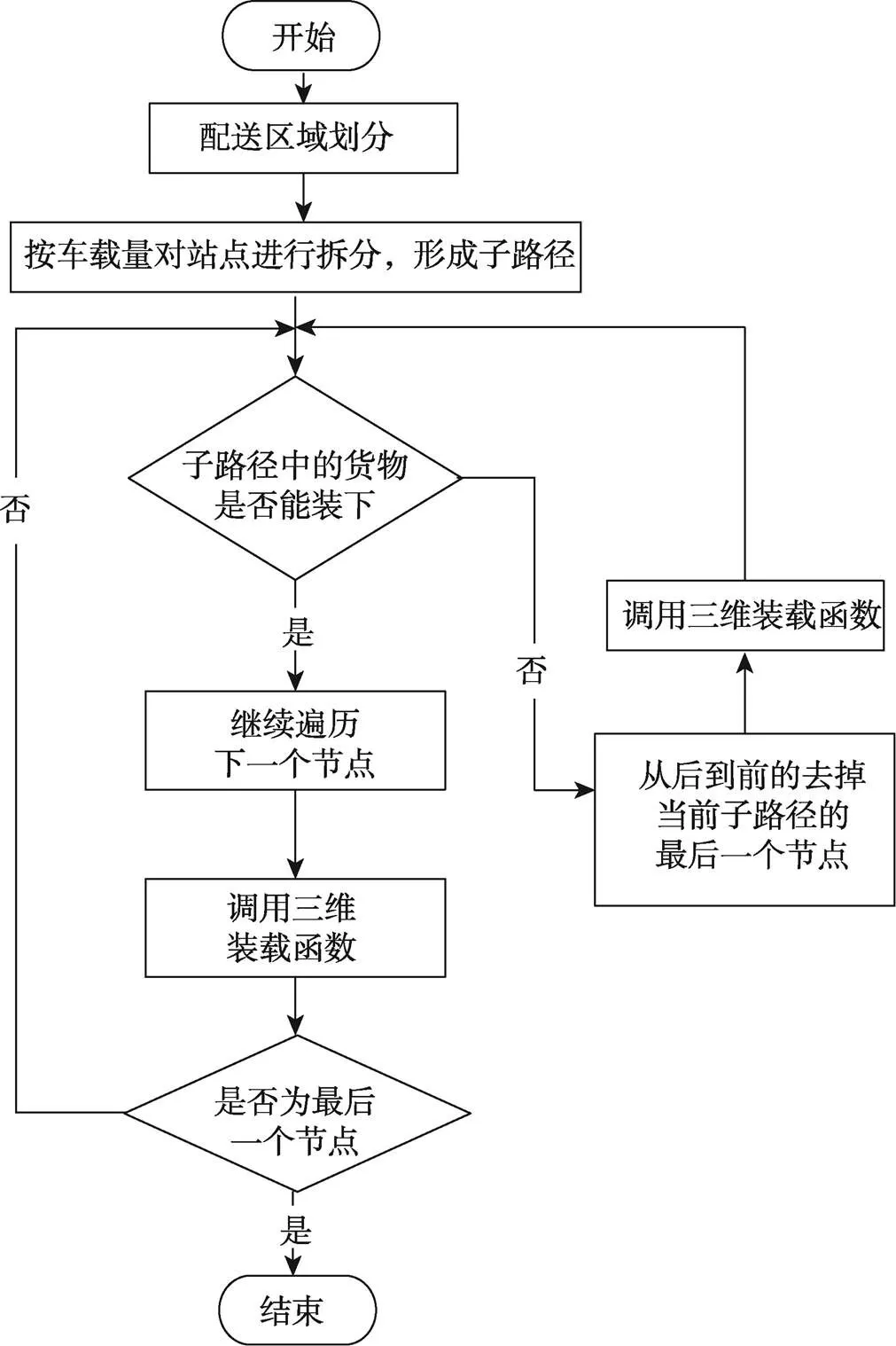
圖3 技術方案的設計框架

3.1 路徑優化算法

3.1.1 路徑優化模型

為使路徑規劃達到最優，配送區域劃分不僅可以節約資源，避免不必要的資源浪費，還可以更好地滿足顧客的需求，及時高效地完成配送計劃。配送區域劃分是根據臨近原則實施的，目的就是配送達到省時、省事、省力，給予顧客最優的體驗，滿足顧客最大的需求。為此在解決路徑優化問題時先使用聚類算法。K-Means聚類算法是一種迭代求解的聚類分析算法，其主要步驟如下：

1）選取個對象作為初始的聚類中心。

2）計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。利用K-means聚類算法的特點依據任意便利店的經緯度坐標進行聚類，對配送區域進行劃分，以得到最優的配送區域劃分。

本文主要運用平均輪廓系數法來求取最優的值。平均輪廓系數法衡量了聚類結果的質量，即衡量每個點被放到當前類簇有多合適，平均輪廓系數很高意味著聚類的結果很好。這種方法計算不同值下所有點的平均輪廓系數，能夠使平均輪廓系數最大的就是最優的類簇數量。

3.1.2 遺傳算法

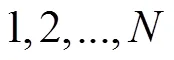
2）適應度的好壞直接影響著染色體的選擇，因文中的目標函數為車輛行駛總距離最短，故設定的適應度函數是目標函數最大值與當前目標函數值的差值，當前目標函數值越小，差值越大，則適應度值越大，染色體越好。

3）染色體的選擇、交叉、變異也會影響遺傳算法的結果。在染色體選擇方面，使用了二元錦標賽法進行選擇，通過隨機選擇2個個體，將適應度值好的留下，重復多次，直至選擇的種群規模達到預先設定的值。

4）交叉方面選擇了OX交叉法進行交叉，在程序編寫中，從種群中隨機選擇2個父代后，再隨機選擇2個交叉點，將父代的中間部分交叉生成子代。交叉后的子代會被添加到模型的解列表中，直到解的數量達到種群數量為止。

5）染色體的變異選擇了二元突變，隨機選擇2個交換位置。通過對染色體交叉、變異概率的改變，可以實現遺傳算法的優化。

將聚類算法與遺傳算法融合后的流程如圖4所示。

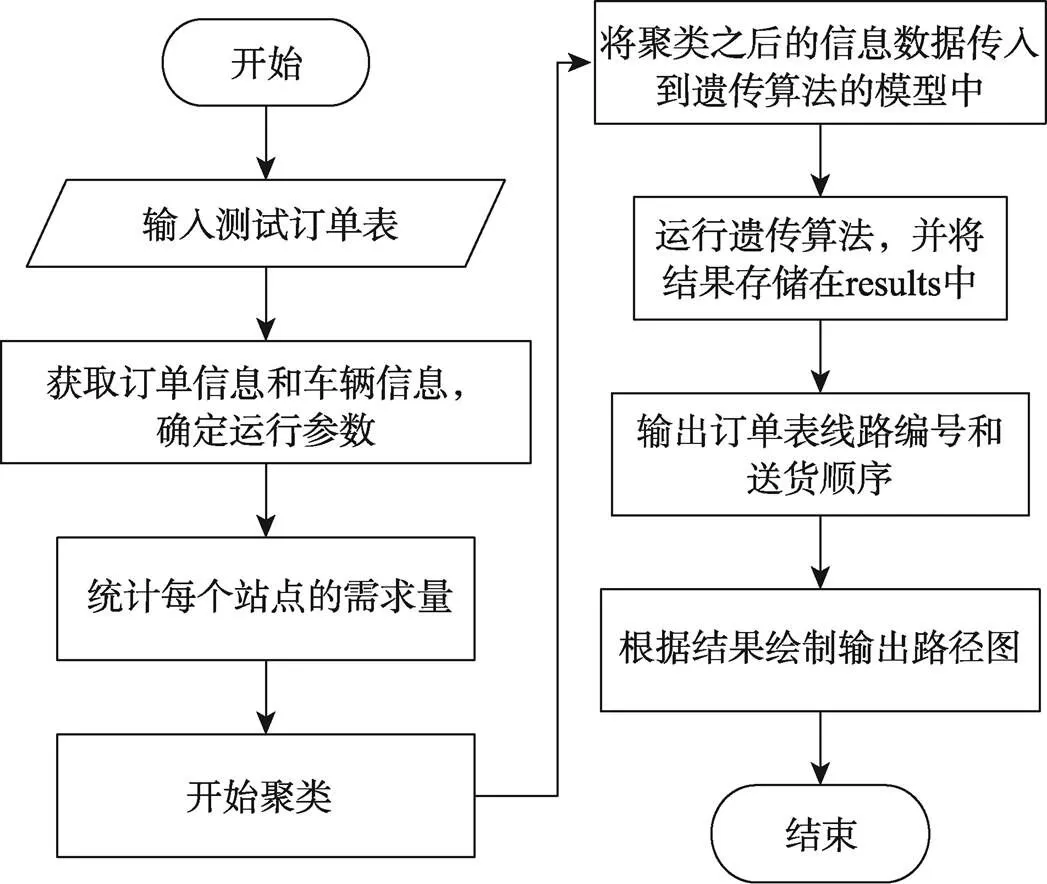
圖4 路徑規劃程序流程

3.2 三維裝載算法

3.2.1 貪心算法

貪心算法主要是在某種意義上的局部最優解。在三維裝載的設計上，對于裝載，首先將貨物按站點分類，一個站點的所有貨箱是一個箱子列表BoxList，每個箱子列表中所有的箱子都按照尺寸大小進行分類，并在每一類里進行質量降序，以便后續同種貨物或同等大小的箱子進行集中裝載。在裝載前需要計算貨車3個方向能放置的最大貨箱個數，判斷貨箱個數是否小于方向可放置個數，若小于則優先方向放置貨箱，否則判斷貨箱個數是否小于×方向可放置個數，若小于則優先×方向放置貨箱，否則優先××方向放置貨箱，以此優先選擇體積最大且寬最大的塊為最優塊chosen。

3.2.2 基于塊裝載的啟發式優化算法

簡單塊是由同一朝向的同種類型的箱子堆疊而成的，箱子和箱子之間沒有空隙，堆疊的結果必須正好形成一個長方體，其生成必須滿足3個條件：簡單塊的長寬高必須在集裝箱的體積范圍內；簡單塊的質量必須在集裝箱的承受范圍內；簡單塊使用的箱子數量必須符合該類箱子的剩余數量。

在每個裝載階段中根據剩余空間大小計算能使用的所有塊，然后從中選擇一個塊裝入剩余空間，這樣在裝載時不會考慮重心約束的條件。已知由貪心算法選出最優塊后，再判斷是否能放入Space空間。若可以放下，將塊放入并標記貨箱的位置，插入第1塊箱子后，每插入一個塊都有3個Space空間，并且每插入一個塊都更新空間列表，對每個塊都可以按照軸旋轉，所有貨箱的重疊部分是需要判斷的，以免出現懸空現象；若不能放下就判斷是否超過oversize的20%，若超過oversize的20%就判斷是否能放下單個貨箱，若不能放置就舍棄該空間，將貨箱放入備用空間，若能放下，判斷目標貨箱放置的位置是否可能被后面的貨物所遮擋，若被遮擋則舍棄該空間，將貨箱放入備用空間，否則放置貨箱并標記貨箱的位置。最后判斷是否為BoxList類里面的最后一個貨箱，若不是就循環BoxList類里面的貨箱，若是就判斷是否為BoxList列表里面的最后一個類，若不是就循環BoxList列表，若是就判斷是否為最后一個站點，若不是就循環站點，若是就判斷是否能全部放入貨車，如果可以放置就返回貨車已裝載的箱子具體位置和裝載率，如果不能就舍棄當前站點，再返回路徑規劃重新尋找可以再裝載的站點。重復上述步驟直至所有站點都可以裝載完成，返回最終車次。

將貪心算法與基于塊裝載的啟發式優化算法相結合后，具體裝載流程如圖5所示。

4 算法實例

本文以某連鎖便利店為例進行研究。該連鎖店共148個站點。配送中心負責向各個便利店運送所需貨物，部分站點的信息如表1所示。通過對連鎖便利店的現狀進行分析，發現在運輸過程中存在行駛道路迂回等情況，配送時人為因素干預較大，由人工隨機配送。根據訂單表中的日期篩選訂單，根據位置信息數據找到收貨人名對應的發貨地編碼，按某一天的車次和客戶單號編號順序計算當前車次的行駛距離，如表2所示。

對148個站點地理位置進行聚類，利用平均輪廓系數法求解的結果如圖6所示。由此可得，當聚類數=5時最優，最終148個站點共分為五部分。

將站點聚類后，利用遺傳算法進行求解，設車輛的最大載質量為5 t，用于配送的車輛足夠多，考慮貨物的體積時，基本參數設置如表3所示，迭代500次，得出的結果如圖7所示，運行時間及運行結果如表4所示。同理，使用另外3種啟發式算法進行求解。4種算法的基本參數設置如表3所示，設車輛的最大載質量為5 t，用于配送的車輛足夠多，考慮貨物的體積時，迭代500次的運行結果如圖7所示，運行時間及運行結果如表4所示。

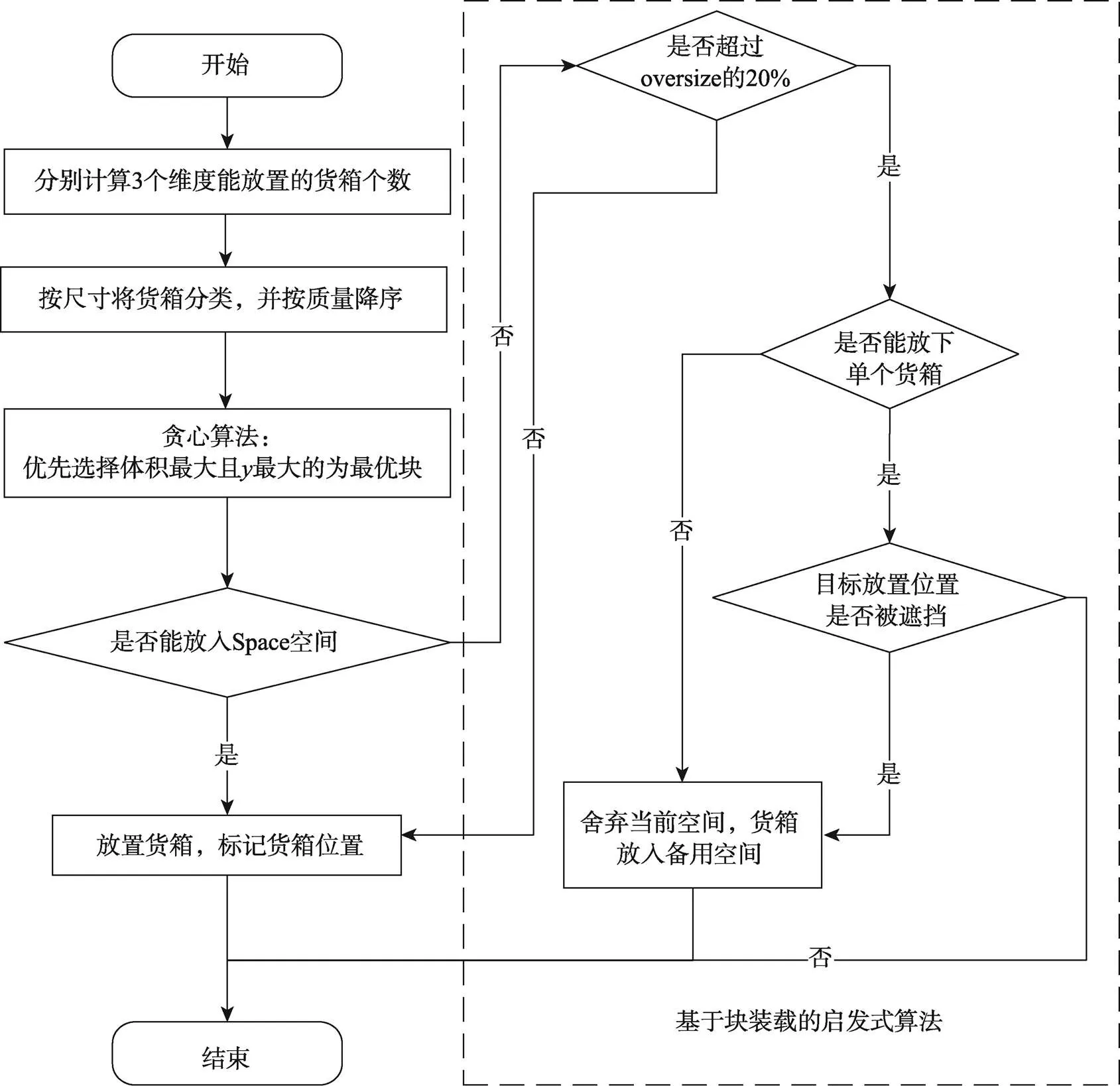
圖5 裝箱算法流程

表1 部分站點的坐標

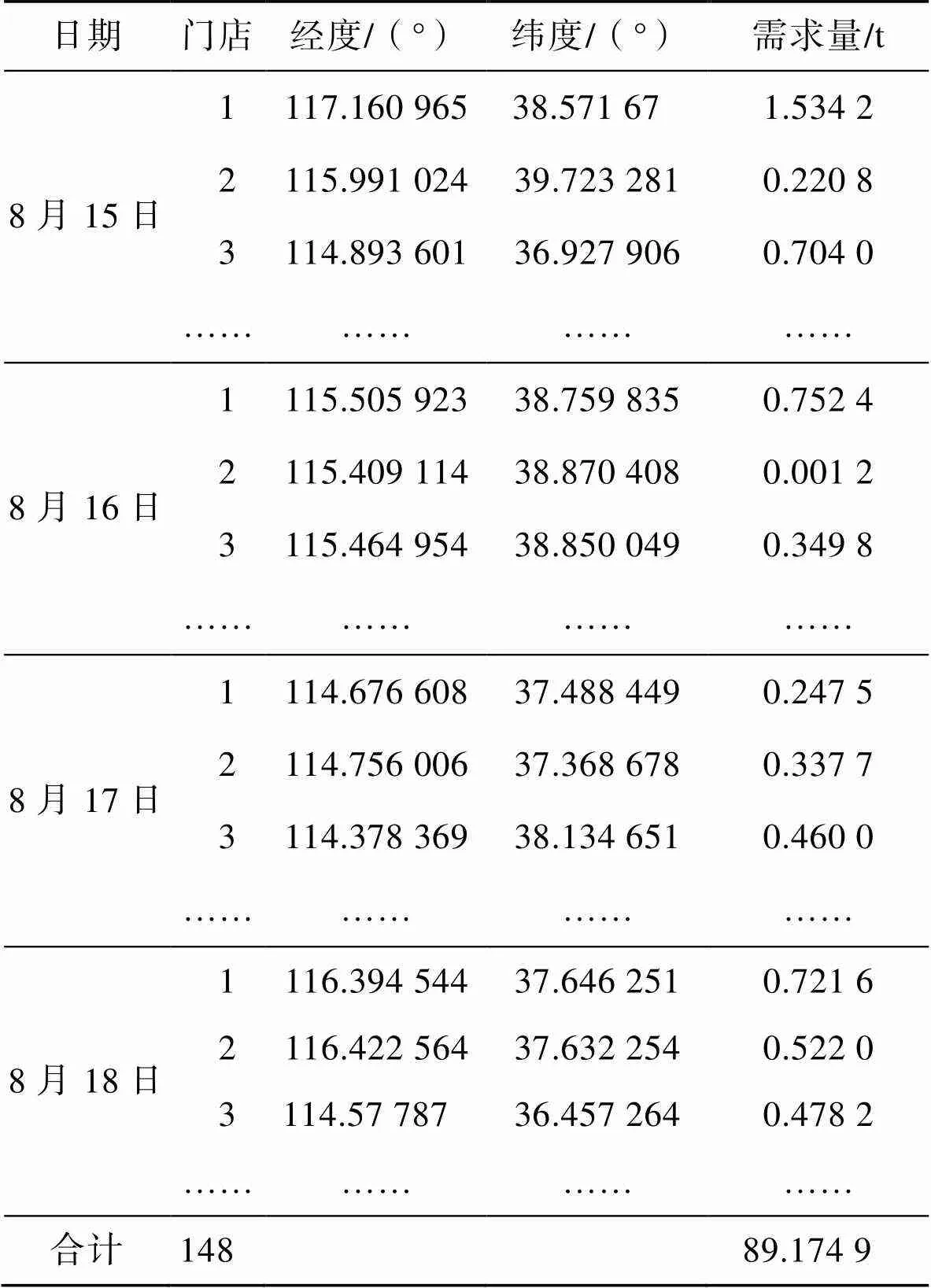
Tab.1 Coordinates of some sites

表2 車輛配送初始數據

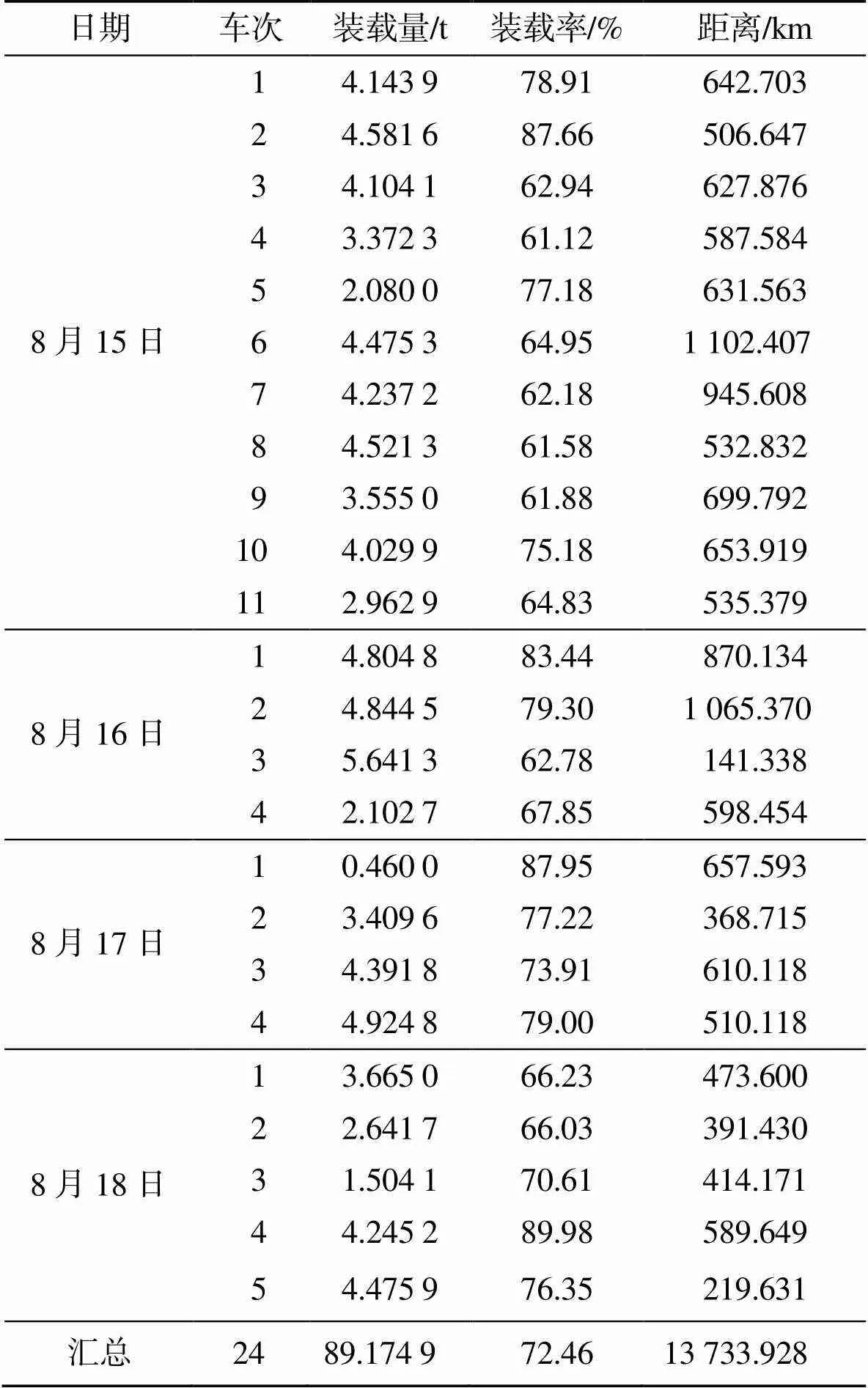
Tab.2 Initial data of vehicle delivery

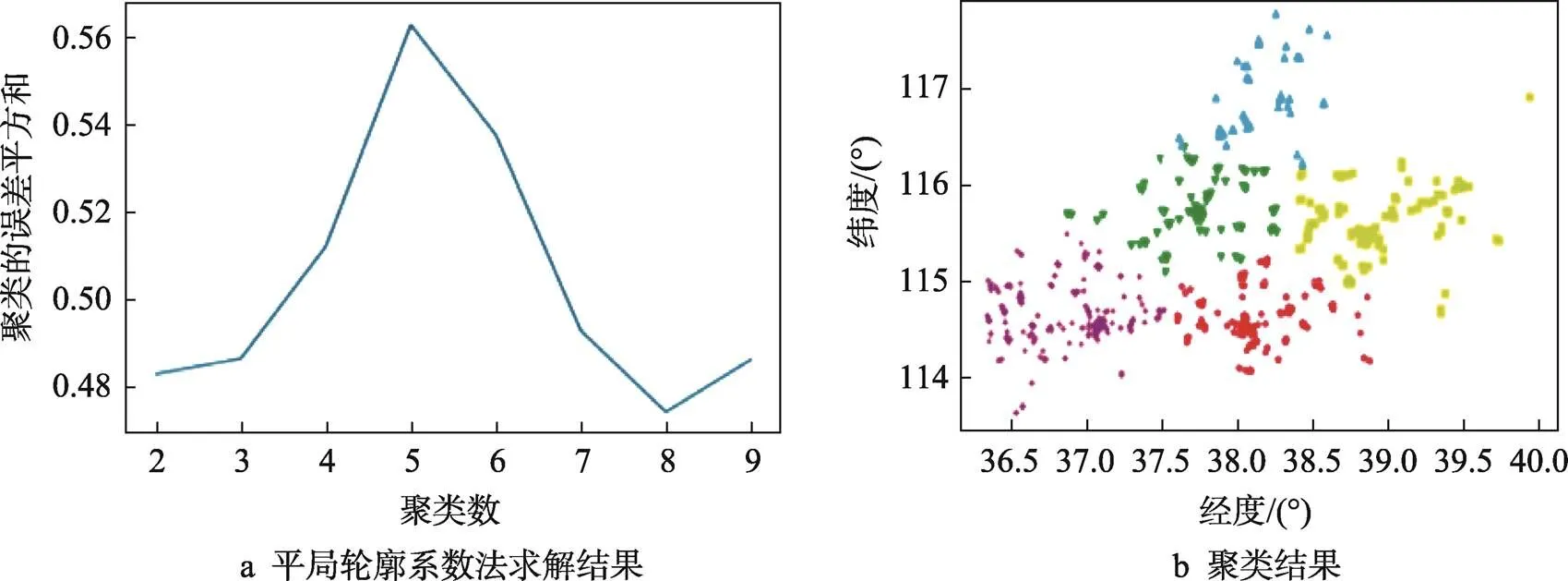
圖6 站點聚類結果

表3 4種啟發式算法參數說明

Tab.3 Parameters explanation of four heuristic algorithms

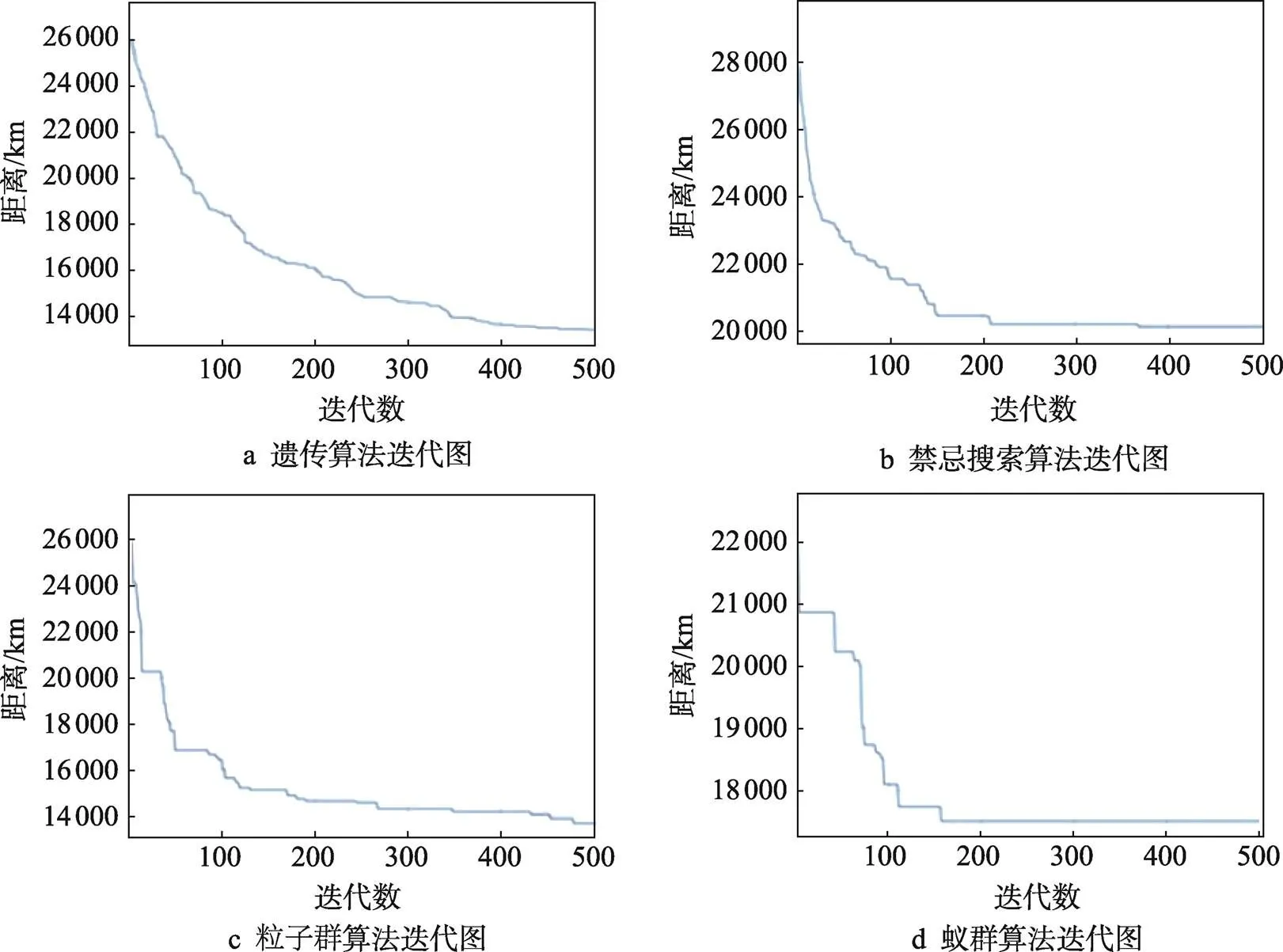
圖7 各算法迭代圖

通過對比4種算法的迭代圖，可以發現禁忌搜索算法和蟻群算法過早收斂的現象較為明顯，粒子群算法也有輕微的陷入局部最優的情況，而遺傳算法一直在向全局最優的結果收斂，雖然最后沒有穩定在某一個數值，但是比其他3種算法更優。

表4 4種啟發式算法運行結果

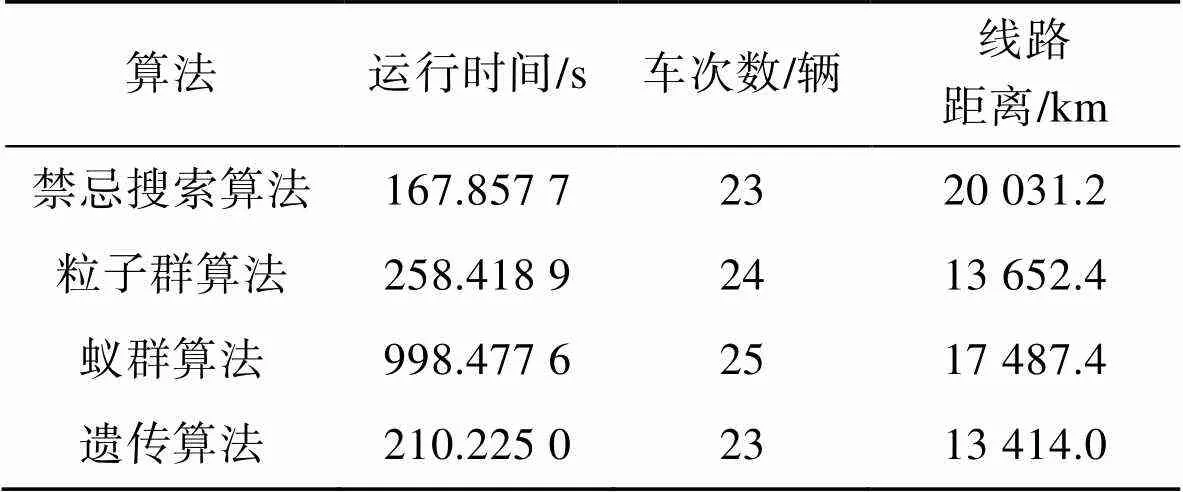
Tab.4 Running results of four heuristic algorithms

由表4對比分析，發現遺傳算法計算出的車次數和路線距離都更為理想，故后續程序設計時采用遺傳算法對構建的模型進行求解。

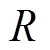
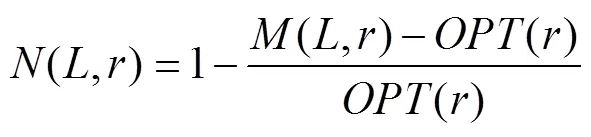
表5 4種啟發式算法性能分析

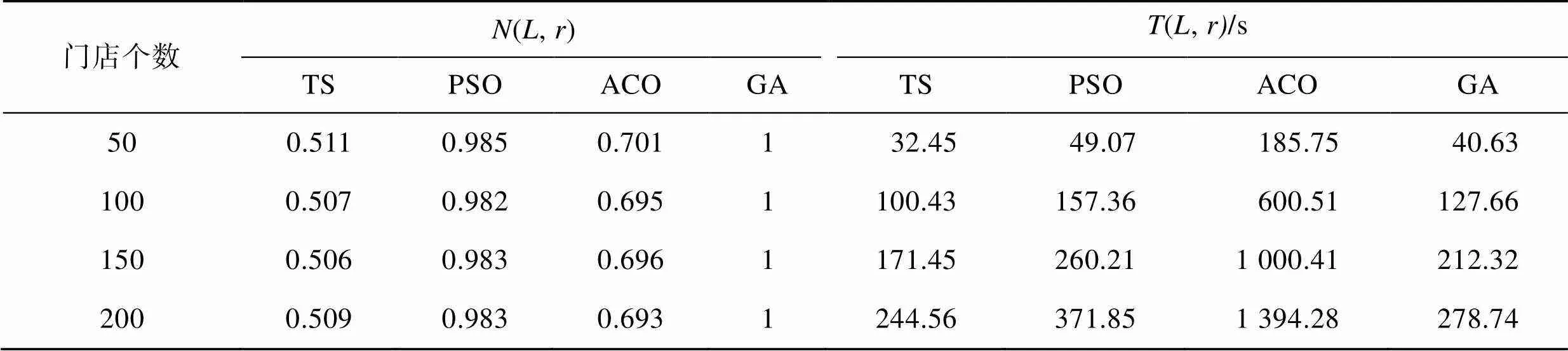
Tab.5 Performance analysis of four heuristic algorithms

由表5可知，隨著求解規模的變大，遺傳算法在性能參數和運行時間方面優勢更加明顯。采取不同的交叉、變異概率進行求解，所求解的行駛車次數均為23輛，具體的路線距離結果如表6所示。

表6 遺傳算法優化結果

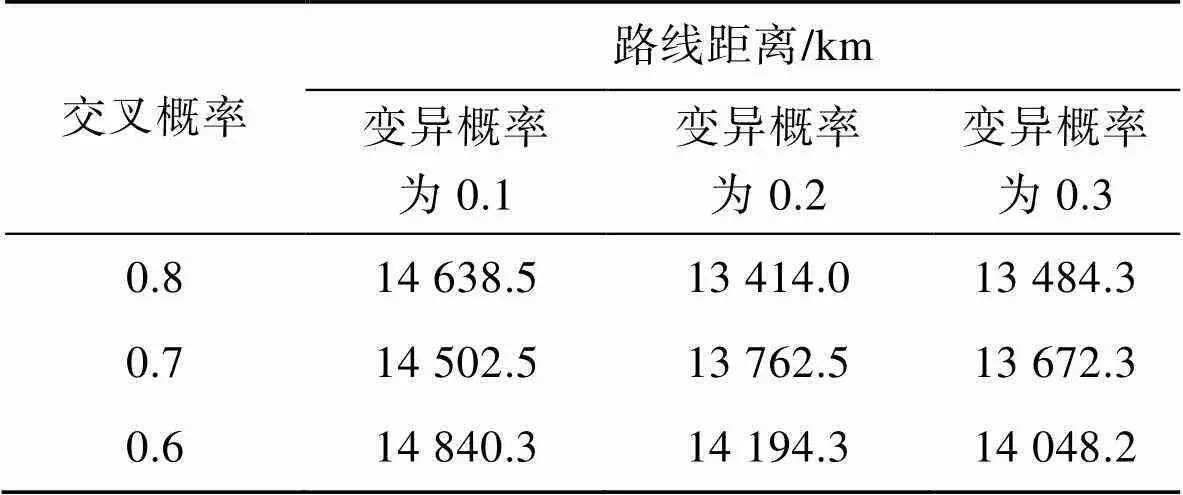
Tab.6 Genetic algorithm optimization results

由表6可知，當交叉概率為0.8，變異概率為0.2時，路線距離最短。

取車輛的最大載質量為5 t，將企業的初始數據利用路徑優化算法與三維裝載算法優化后形成的配送路線結果如表7所示，配送路徑如圖8所示。

4種優化算法與三維裝載算法相結合形成的三維裝載部分展示如圖9所示。表8展示了優化前后相關優化結果的變化情況，其中優化前指人工隨機配送的結果，優化后指利用遺傳算法為主的路徑優化算法和三維裝載算法的優化結果。

表7 優化結果

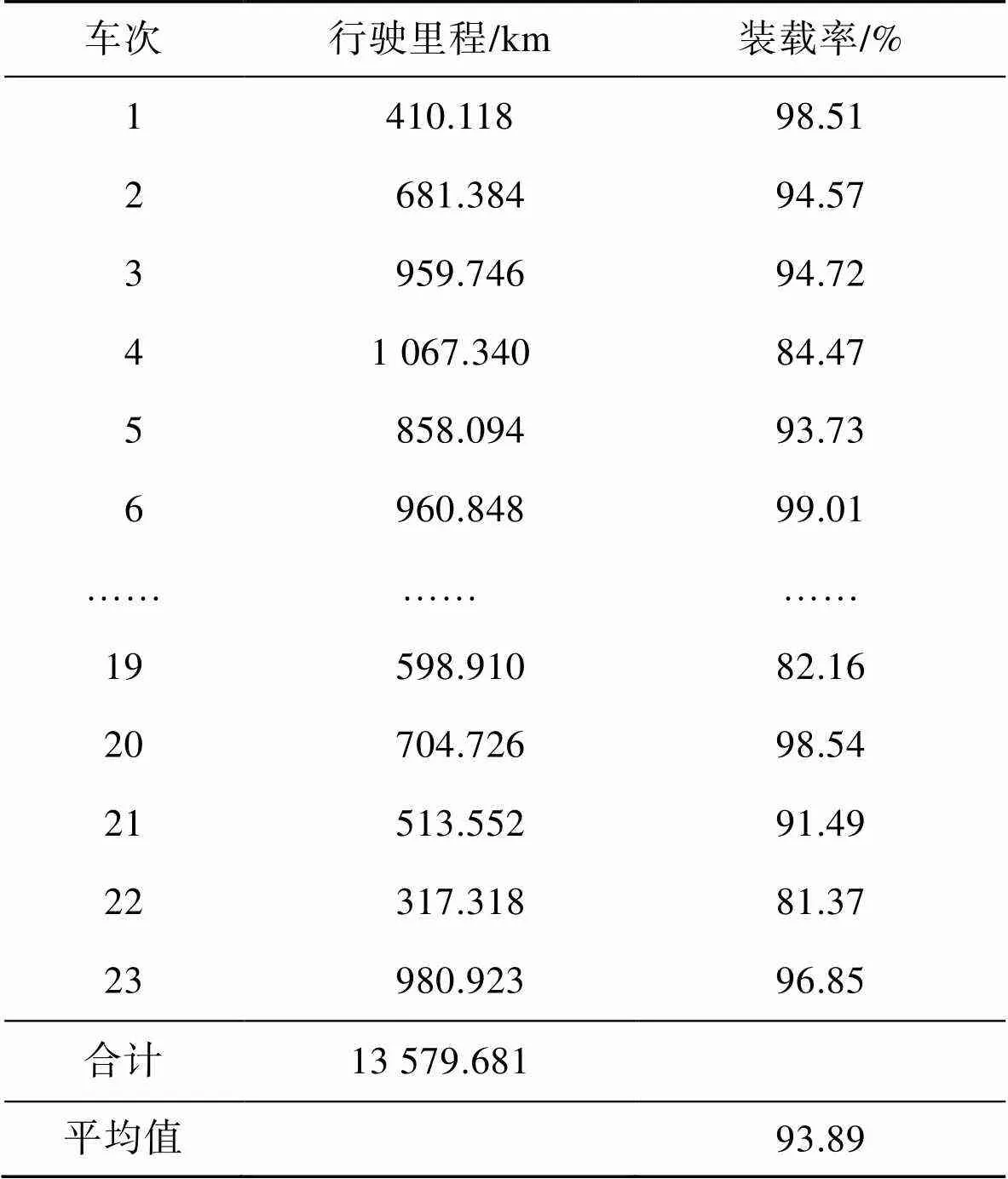
Tab.7 Optimal results

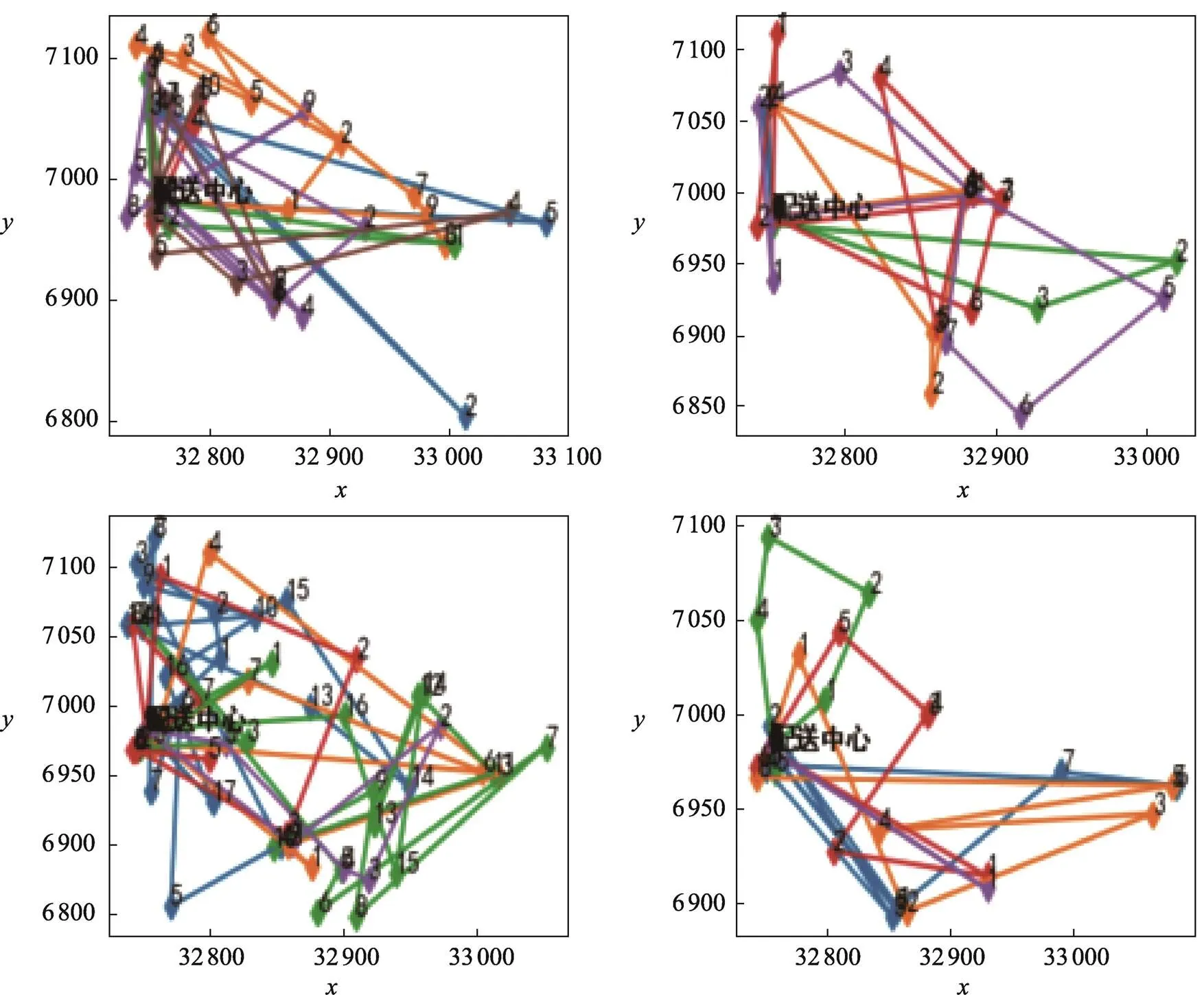
圖8 優化后的路線結果

圖9 三維裝載展示

表8 優化前后相關結果對比

Tab.8 Comparison of relevant results before and after optimization

優化后的車輛配送區間更加聚集，由圖10可以看出遺傳算法求解的裝載率最高。由表8可知，優化前后結果對比，配送的車輛減少了1輛，配送距離減少了154.247 km，使用聚類算法、遺傳算法、貪心算法、基于塊的啟發式算法4種算法相結合的方式，使得車輛達到了較高的裝載率，平均裝載率達到了93.89%，節省了企業的配送成本。

5 結語

配送路徑與連鎖便利店的生產經營有著密不可分的關系。本文根據存在的單一車型考慮質量與體積的配送路徑問題，建立了相應的路徑優化模型與三維裝載模型，并利用聚類算法和遺傳算法進行解決，在遺傳算法求解過程中調用解決三維裝載的貪心算法與基于塊的啟發式算法，通過前后對比發現該算法降低了車輛的使用數量，車輛的裝載率較高，為便利店節省了配送成本，優化的結果科學合理。

在算法的求解過程中還存在不足之處，未來三維裝載關于貨物的承重、貨物的重心與平衡以及如何優化貨物的裝載效率和裝載時間仍需繼續研究，進一步完善三維裝載的程序代碼，實現高效裝載。

[1] DANTZIG G B，RAMSER J H. The Truck Dispatching Problem[J]. Management Science, 1959, 6(1): 80-91.

[2] AGáRDI A, KOVáCS L, BáNYAI T. Mathematical Model for the Generalized VRP Model[J]. Sustainability, 2022, 14(18): 1639.

[3] JOANNA O, ANETA P, WITOLD M. Selected Genetic Algorithms for Vehicle Routing Problem Solving[J]. Electronics, 2021, 10(24): 3147.

[4] OLANIYI O S, JAMES A K, IBRAHIM A A, et al. On the Application of a Modified Genetic Algorithm for Solving Vehicle Routing Problems with Time Windows and Split Delivery[J]. IAENG International Journal of Applied Mathematics, 2022, 52(1): 1-9.

[5] 靳康飛, 閆軍, 梁云濤. 容量約束的車輛路徑問題研究現狀綜述[J]. 甘肅科技縱橫, 2022, 51(10): 52-56.

JIN K F, YAN J, LIANG Y T. A Review of the Current State of Research on the Capacited Vehicle Routing Problems[J]. Scientific & Technical Information of Gansu, 2022, 51(10): 52-56.

[6] SIMENSEN M, HASLE G, ST?LHANE M. Combining Hybrid Genetic Search with Ruin-and-Recreate for Solving the Capacitated Vehicle Routing Problem[J]. Journal of Heuristics, 2022, 28(5): 653-697.

[7] 梁彪, 嚴昌龍. 一種求解CVRP問題的遺傳蟻群融合算法[J]. 中國物流與采購, 2021(24): 34-35.

LIANG B, YAN C L. A Genetic Ant Colony Fusion Algorithm for Solving CVRP Problems[J]. China Logistics & Purchasing, 2021(24): 34-35.

[8] THANGIAH S R, SALHI S. Genetic Clustering: An Adaptive Heuristic for the Multidepot Vehicle Routing Problem[J]. Applied Artificial Intelligence, 2001, 15(4): 361-383.

[9] LUO J, CHEN M R. Multi-Phase Modified Shuffled Frog Leaping Algorithm with Extremal Optimization for the MDVRP and the MDVRPTW[J]. Computers & Industrial Engineering, 2014, 72: 84-97.

[10] 王超, 金淳, 韓慶平. 三維裝載與CVRP聯合多目標優化問題的模型及算法[J]. 控制與決策, 2016, 31(5): 929-934.

WANG C, JIN C, HAN Q P. Model and Algorithm for Multi-Objective Joint Optimization of Three-Dimensional Loading and CVRP[J]. Control and Decision, 2016, 31(5): 929-934.

[11] 那日薩, 韓琪瑋, 林正奎. 三維多箱異構貨物裝載優化及其可視化[J]. 運籌與管理, 2015, 24(4): 76-82.

NA R S, HAN Q W, LIN Z K. Optimization and Visualization of Multiple 3 D Container Loading Problem with Non-Identical Items[J]. Operations Research and Management Science, 2015, 24(4): 76-82.

[12] YAN X X, WANG G R, JIANG K S, et al. Multi-Objective Scheduling Strategy of Mine Transportation Robot Based on Three-Dimensional Loading Constraint[J]. Minerals, 2023, 13(3): 431.

[13] LIU Y, YUE Z C, WANG Y, et al. Logistics Distribution Vehicle Routing Problem with Time Window under Pallet 3D Loading Constraint[J]. Sustainability, 2023, 15(4): 3594.

[14] 王勇, 魏遠晗, 蔣瓊, 等. 三維裝載約束下基于運輸資源共享的車輛路徑問題[J]. 計算機集成制造系統, 2023, 29(9): 3153-3170.

WANG Y, WEI Y H, JIANG Q, et al. Vehicle Routing Problem Based on Transportation Resource Sharing under Three-Dimensional Loading Constraints[J]. Computer Integrated Manufacturing Systems, 2023, 29(9): 3153-3170.

[15] 崔會芬, 許佳瑜, 楊京帥, 等. 基于遺傳算法的3L-CVRP優化問題研究[J]. 交通信息與安全, 2018, 36(5): 124-131.

CUI H F, XU J Y, YANG J S, et al. An Optimization of 3L-CVRP Based on a Genetic Algorithm[J]. Journal of Transport Information and Safety, 2018, 36(5): 124-131.

Joint Optimization of Vehicle Loading and Distribution Routes under Dual Constraints of Quality and Volume

REN Zongwei1*, QIAN Zhijun2, ZHENG Wei2, PU Wei3, ZHANG Ning3,QI Binbin2

(1. School of Management, Harbin University of Commerce, Harbin 150028, China; 2. Kunlun Digital Intelligence Technology Co., Ltd., Beijing 100000, China; 3. China National Petroleum Corporation Hebei Sales Branch, Shijiazhuang 050000, China)

The work aims to constructa joint optimization model for vehicle loading and distribution routes with the shortest route and the highest loading rate, taking into account constraints such as the indivisibility of orders and the volume of goods, so as to address the delivery route problem with common limitations of quality and volume. In terms of solving the vehicle route optimization model, first the clustering algorithm was used to partition the distribution area, and then the load capacity of the vehicle was used to determine whether the station goods could be delivered. Finally, the genetic algorithm was used to obtain the optimal route. The greedy algorithm and the block based heuristic algorithm were used to solve the loading problem of goods in the 3D loading model. The feasibility of the model and the algorithm was verified based on a specific example of a company. After optimization, the number of vehicles for delivery was reduced by 1, the delivery distance was reduced by 154.247 km, and the average loading rate reached 93.89%, saving the company's delivery costs. The results indicate that the constructed model and the solved algorithm can improve loading rate and delivery efficiency, providing a theoretical basis for solving the joint optimization problem of vehicle loading and distribution routes.

route optimization; genetic algorithm; 3D loading; block based heuristic algorithm

TB485.3；F540

A

1001-3563(2024)09-0232-11

10.19554/j.cnki.1001-3563.2024.09.030

2023-10-20

國家自然科學基金（71371061）；國家重點研發計劃（2018YFB1402500）；黑龍江省哲學社會科學資助項目（23RKB134）；黑龍江省自然科學基金項目（LH2023G009）