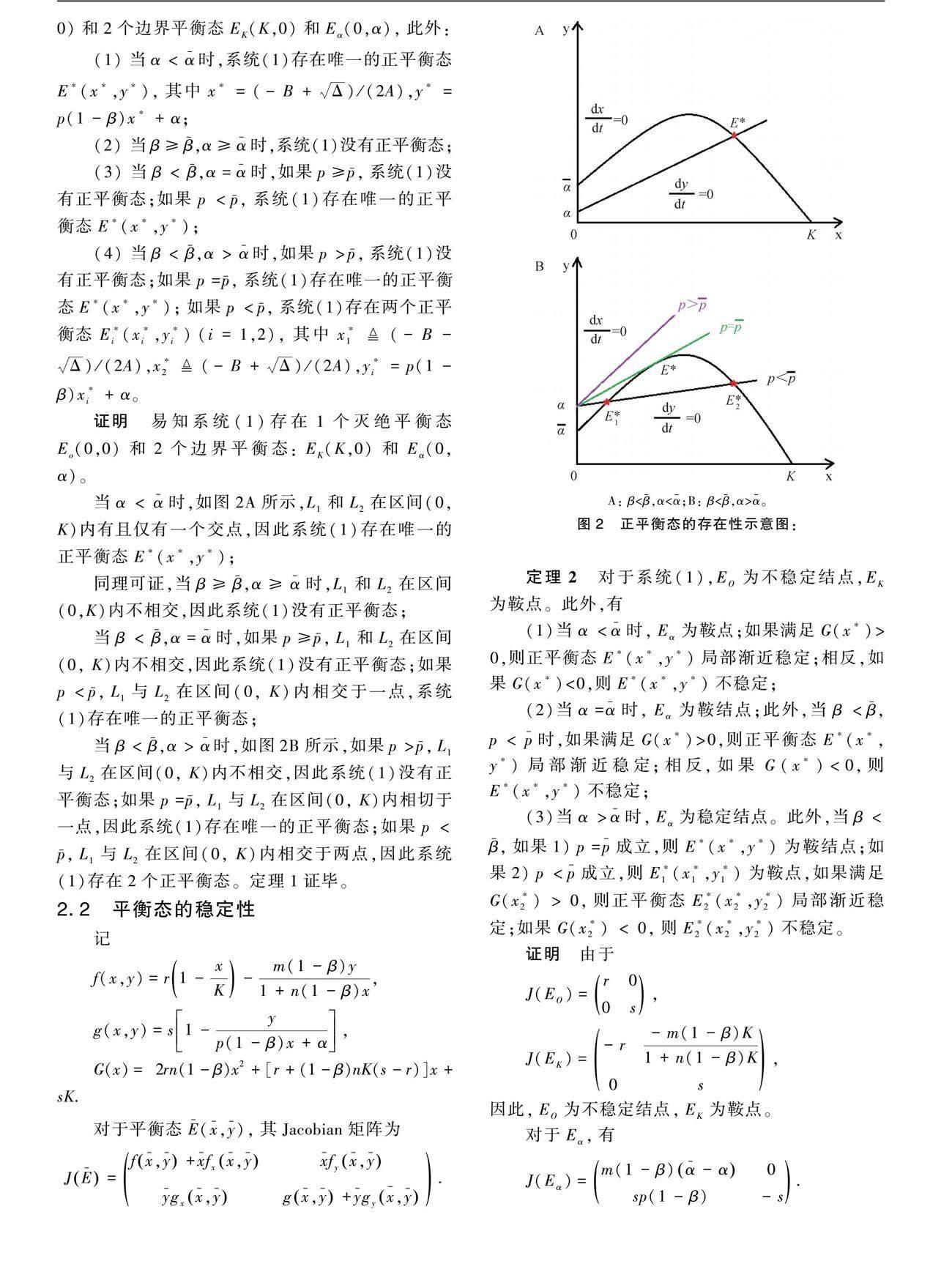
草履蚧綜合治理模型動力學(xué)性態(tài)分析

王靜雨 田源 勞永瀚 林佳雯 周呂佳

摘要：草履蚧在我國大部分地區(qū)都有分布， 通過吸食樹液致使樹勢衰弱， 甚至枝條枯死， 影響產(chǎn)量。本文在對草履蚧及其天敵大紅瓢蟲之間相互關(guān)系分析的基礎(chǔ)上， 首先建立了一個具有避難所效應(yīng)及額外食物來源的捕食-被捕食模型， 分析了系統(tǒng)平衡態(tài)及極限環(huán)的存在性和穩(wěn)定性。其次， 從控制草履蚧蔓延角度出發(fā)， 建立了一個具有狀態(tài)反饋的草履蚧綜合治理模型，利用后繼函數(shù)的方法證明了系統(tǒng)階-1周期解的存在性，并借助類似龐加萊準(zhǔn)則給出了階-1周期解軌道漸近穩(wěn)定性條件。最后，利用MATLAB對文中所取得的主要結(jié)論進(jìn)行了仿真驗證。本文研究為草履蚧綜合治理提供了新的思路和方法。

關(guān)鍵詞：草履蚧；避難所效應(yīng)；額外食物；Leslie-Gower模型；綜合治理

中圖分類號：O175文獻(xiàn)標(biāo)志碼：A文獻(xiàn)標(biāo)識碼

Dynamic analysis of a Drosicha corpulenta integrated management model

WANG? Jingyu，TIAN? Yuan*，LAO? Yonghan，LIN? Jiawen，ZHOU? Lüjia

（School of Science， Dalian Maritime University，Dalian，Liaoning 116026， China）

Abstract： Drosicha corpulenta is distributed in most areas of our country. It causes tree weakness， even branches dying， and affects yield by sucking tree SAP. In this paper， a predator-prey model with shelter effect and additional food source is established based on the relationship analysis between the Drosicha corpulenta and the Rodolia rufopilosaMuls. The existence and stability of equilibria and the limit cycle are analyzed. Secondly， from the point of view of controlling the spread of the Drosicha corpulenta， an integrated management model based on state-feedback is established. The existence of the order-1 periodic solution of the system is proved by the method of successor function， and the asymptotic stability condition of the order-1 periodic solution is given by means of Analogue Poincar criterion. Finally， the main results are verified by MATLAB simulations. The research in this paper provides a new idea and method for integrated management of Drosicha corpulenta.

Key words： Drosicha corpulenta;shelter effect;additional food;Leslie-Gower model;integrated management

在自然界中，不同生物種群以及同一種群中不同個體間相互依賴， 彼此之間形成了捕食、競爭、共生、寄生等相互作用關(guān)系。而捕食-被捕食關(guān)系作為自然界中普遍存在的生物關(guān)系，在促進(jìn)生物種間能量循環(huán)和維護(hù)生態(tài)系統(tǒng)穩(wěn)定性中發(fā)揮著十分重要的作用。因此，合理的利用生物種群之間的捕食與被捕食關(guān)系，可以達(dá)到有效控制害蟲種群數(shù)量增長的效果。

草履蚧是一種分布廣泛、危害嚴(yán)重的害蟲，其對植株生長以及人類生產(chǎn)生活均造成了嚴(yán)重的干擾［1］。大紅瓢蟲是草履蚧的自然天敵，對草履蚧的蔓延起到了一定的抑制作用［2］。因此，借助于捕食-被捕食關(guān)系對其進(jìn)行研究，可以指導(dǎo)草履蚧防治過程，具有重要應(yīng)用價值。針對生物種群中捕食者與食餌之間的關(guān)系，Leslie等［3］首次引入Leslie-Gower模型，自此開啟了對Leslie-Gower模型及其改進(jìn)的廣泛研究［4-13］，其中Chen等［4］在Holling-I型Leslie-Gower模型基礎(chǔ)上引入了避難所效應(yīng)，Guan等［5］在改進(jìn)Holling-II型Leslie-Gower模型基礎(chǔ)上引入了避難所效應(yīng)，Wang等［6］在Leslie-Gower模型中引入了恐懼效應(yīng)，Claudio等［9］和Fang等［10］在Leslie-Gower模型中引入了Allee效應(yīng)，Li等［11］和Liu等［13］ 在Leslie-Gower模型中引入了Allee和恐懼雙重效應(yīng)。此外，針對害蟲綜合治理問題，Song等［14］在改進(jìn)Holling-II型Leslie-Gower模型基礎(chǔ)上引入了周期脈沖控制，Nie等［15］在改進(jìn)Holling-II型Leslie-Gower模型基礎(chǔ)上引入了狀態(tài)依賴反饋控制，Xu等［16］在改進(jìn)比例依賴型Leslie-Gower模型基礎(chǔ)上引入了狀態(tài)依賴反饋控制，等等。

在長期自然進(jìn)化過程中，為了躲避大紅瓢蟲的捕食，部分草履蚧及幼蟲會選擇躲避在茂密的枝葉中，進(jìn)而降低被捕食的概率；另一方面，當(dāng)草履蚧種群數(shù)量較少時，大紅瓢蟲也可以通過攝食其它生物來補(bǔ)充自身生物量。基于以上考慮，本文建立了一個具有食餌避難所效應(yīng)以及捕食者額外食物來源的Leslie-Gower模型，分析額外食物數(shù)量和避難所系數(shù)對系統(tǒng)動力學(xué)的影響。同時在此基礎(chǔ)上，建立草履蚧綜合治理模型，探討反饋控制策略誘導(dǎo)的系統(tǒng)復(fù)雜動力學(xué)。

4 數(shù)值模擬

為了驗證文中所取得的主要結(jié)論，對于系統(tǒng)（1），主要參數(shù)取：r=1.2，s=0.4，K=100，m=0.8，n=0.4。由此可計算得β-=0.975。下面擬通過調(diào)整β，α和p的值來進(jìn)行驗證。

4.1 連續(xù)動力系統(tǒng)數(shù)值模擬

（1） 取α=0.3<α-，此時系統(tǒng)（1）存在唯一的正平衡態(tài)。

1） 取β=0.2<β-。當(dāng)p=0.25時，如圖4A所示，E* （67.43， 13.79）穩(wěn)定（G（67.43）>0）；當(dāng)p=0.5時，如圖4B所示，E*（37.25， 15.2）穩(wěn)定（G（37.25）>0）；當(dāng)p=0.625時，如圖4C所示，E*（24.33， 12.47）不穩(wěn)定，此時系統(tǒng)（1）存在極限環(huán)；當(dāng)p=2.5時，如圖4D所示，E*（1.1， 2.5）局部穩(wěn)定，在E*（1.1，2.5）外圍存在穩(wěn)定的極限環(huán)，即系統(tǒng)（1）存在雙穩(wěn)態(tài)。

此外，G（x*）>0等價于0

2） 取β=0.98>β-。當(dāng)p=0.5時，如圖5A所示，E*（69.87，35.23）局部漸近穩(wěn)定。此外，由圖5B可知，G（x）>0恒成立，即對于任意的p>0，正平衡態(tài)E*均局部漸近穩(wěn)定。

（2） α>α-。取β=0.5，此時有α-=3。取α=5。當(dāng)p=0.2時，如圖6A所示，此時E*1（5.99，6.2）為鞍點(diǎn)，E*2（55.68，16.14）為穩(wěn)定結(jié)點(diǎn)（G（55.68）>0）；當(dāng)p=0.32時，如圖6B所示，E*1（10.8，8.46）為鞍點(diǎn)，E*2（30.87，14.88）為穩(wěn)定結(jié)點(diǎn)（G（30.87）>0）；當(dāng)p=0.34時，如圖6C所示，E*1（13.33，9.53）為鞍點(diǎn)，E*2（25，13.5）為不穩(wěn)定結(jié)點(diǎn)（G（25）<0）。

4.2 綜合治理模型數(shù)值模擬

為了驗證定理4，取模型參數(shù)β=0.5，α=0.3，p=0.25。控制參數(shù)選取為：k1=0.5，k2=0.2。首先，對于xH=60％K

對于x-H

5 結(jié)論

針對草履蚧綜合治理問題，建立了一類具有避難所效應(yīng)及額外食物來源的捕食-被捕食模型，分析了系統(tǒng)的動力學(xué)性態(tài)。研究結(jié)果表明，避難所效應(yīng)和額外食物來源對系統(tǒng)正平衡態(tài)存在性及穩(wěn)定性有一定的影響：當(dāng)額外食物量較小時（即α<α-），系統(tǒng)肯定存在正平衡態(tài)，其局部穩(wěn)定性依賴于捕食者對食餌的依賴程度p；當(dāng)捕食者額外食物量較大時（即α>α-），如果選擇避難食餌比例超過一定閾值（即β≥β-），則系統(tǒng)不存在正平衡態(tài)；如果選擇避難的食餌比例低于某個閾值（即β<β-），則系統(tǒng)存在正平衡態(tài)，其數(shù)量及其穩(wěn)定性依賴于p的大小（定理1， 2）。

為了防止草履蚧數(shù)量過大對環(huán)境造成危害，通過對草履蚧數(shù)量進(jìn)行監(jiān)測，建立了基于狀態(tài)反饋的草履蚧綜合治理模型。利用后繼函數(shù)方法討論了系統(tǒng)階-1周期解的存在性（定理4，圖7），并利用類龐加萊準(zhǔn)則給出階-1周期解的穩(wěn)定性（定理5，圖7）。研究結(jié)果表明，為防止草履蚧數(shù)量過大而危害生態(tài)環(huán)境，通過人為向系統(tǒng)中投放天敵及噴灑殺蟲劑等方式，可以將草履蚧數(shù)量有效控制在可接受水平，進(jìn)而達(dá)到草履蚧綜合治理的目的和效果。

本文研究是對草履蚧綜合防治的理論探討，數(shù)值模擬僅限于驗證文中主要結(jié)論的正確性，而在實際的草履蚧防治過程中，需要結(jié)合實際情況以及統(tǒng)計數(shù)據(jù)來辨識模型參數(shù)以及控制參數(shù)，再結(jié)合文中主要結(jié)論來預(yù)測控制效果，進(jìn)而對草履蚧綜合防治提供理論方法和參考依據(jù)。

參考文獻(xiàn)（References）

［1］ 任善軍. 菊花桃上草履蚧的綠色防治方法［J］. 果農(nóng)之友， 2019（2）： 29.

REN S J. Green prevention and control methods of Drosicha corpulenta in chrysanthemum and peach［J］. Fruit Growers′ Friend， 2019（2）： 29.

［2］ 李曉云. 淺談楊樹草履蚧防治［J］. 農(nóng)家參謀， 2019（21）： 69.

LI X Y. Discussion on prevention and control of Drosicha corpulenta in poplar［J］. The Farmers Consultant， 2019（21）： 69.

［3］ LESLIE P H. Some further notes on the use of matrices in population mathematics［J］. Biometrika， 1948， 35 （3-4）： 213-245.

［4］ CHEN F D， CHEN L J， XIE X D. On a Leslie-Gower predator-prey model incorporating a prey refuge［J］. Nonlinear Analysis： Real World Applications， 2009， 10（5）： 2905-2908.

［5］ GUAN X N， WANG W M， CAI Y L. Spatiotemporal dynamics of a Leslie-Gower predator-prey model incorporating a prey refuge［J］. Nonlinear Analysis： Real World Applications， 2011， 12（4）： 2385-2395.

［6］ CHAKRABORTY K， DAS K， YU HG. Modeling and analysis of a modified Leslie-Gower type three species food chain model with an impulsive control strategy［J］. NONLINEAR ANALYSIS-HYBRID SYSTEMS， 2015， 15： 171-184.

［7］ SIVASAMY R， SATHIYANATHAN K， BALACHANDRAN K. Dynamics of a modified Leslie-Gower model with Crowley-Martin functional response and prey harvesting［J］. Journal of Applied Nonlinear Dynamics， 2019， 8（4）： 621-636.

［6］ WANG X Q， TAN Y P， CAI Y L， et al. Impact of the fear effect on the stability and bifurcation of a Leslie-Gower predator-prey model［J］. International Journal of Bifurcation and Chaos， 2020， 30（14）： 2050210.

［7］ GIN J， VALLS C. Nonlinear oscillations in the modified Leslie-Gower model［J］. Nonlinear Analysis： Real World Applications， 2020， 51： 103010.

［8］ LI L， ZHAO W C. Deterministic and stochastic dynamics of a modified Leslie-Gower prey-predator system with simplified Holling-type IV scheme［J］. Mathematical Biosciences and Engineering， 2021， 18（3）： 2813-2831.

［9］ ARANCIBIA-IBARRA C， FLORES J. Dynamics of a Leslie-Gower predator-prey model with Holling type II functional response， Allee effect and a generalist predator［J］. Mathematics and Computers in Simulation， 2021， 188： 1-22.

［10］ FANG K， ZHU Z L， CHEN F D， et al. Qualitative and bifurcation analysis in a Leslie-Gower model with Allee effect［J］. Qualitative Theory of Dynamical Systems， 2022， 21（3）：86.

［11］ LI Y J， HE M X， LI Z. Dynamics of a ratio-dependent Leslie-Gower predator-prey model with Allee effect and fear effect［J］. Mathematics and Computers in Simulation， 2022， 201： 417-439.

［12］ HE M X， LI Z. Global dynamics of a Leslie-Gower predator-prey model with square root response function［J］. Applied Mathematics Letters， 2023， 140： 108561.

［13］ LIU T T， CHEN L J， CHEN F D， et al. Dynamics of a Leslie-Gower model with weak Allee effect on prey and fear effect on predator［J］. International Journal of Bifurcation and Chaos， 2023， 33（1）： 2350008.

［14］ SONG X Y， LI Y F. Dynamic behaviors of the periodic predator-prey model with modified Leslie-Gower Holling-type II schemes and impulsive effect［J］. Nonlinear Analysis： Real World Applications， 2008， 9（1）： 64-79.

［15］ NIE L F， TENG Z D， HU L， et al. Qualitative analysis of a modified Leslie-Gower and Holling-type II predator-prey model with state dependent impulsive effects［J］. Nonlinear Analysis： Real World Applications， 2010， 11（3）： 1364-1373.

［16］ XU J， TIAN Y， GUO H J， et al. Dynamical analysis of a pest management Leslie-Gower model with ratio-dependent functional response［J］. Nonlinear Dynamics， 2018， 93（2）： 705-720.

［17］ 田源， 李春雪，劉婧. 基于線性依賴的競爭系統(tǒng)脈沖控制與優(yōu)化［J］. 應(yīng)用數(shù)學(xué)， 2023， 36（2）： 523-529.

TIAN Y， LI C X， LIU J. Impulsive control and optimization of a competing system based on linear dependence［J］. Mathematic Applicata， 2023， 36（2）： 523-529.

［18］ 田源， 李幻夢. 基于合作狩獵的捕食者-食餌系統(tǒng)定性分析與反饋控制［J］. 信陽師范學(xué)院學(xué)報（自然科學(xué)版）， 2023， 36（1）： 22-27.

TIAN Y， LI H M. Qualitative analysis and feedback control of predator-prey model based on cooperative hunting effect［J］. Journal of Xinyang Normal University （Natural Science Edition）， 2023， 36（1）： 22-27.

（責(zé)任編輯：編輯郭蕓婕）