“參數方程”的高三數學第一輪專題復習課例
? 上海市南匯第一中學 楊玉燦
1 考點分析
參數方程是理科數學選修4-4的內容,主要包括:參數方程的概念、直線的參數方程、圓的參數方程、橢圓的參數方程等.同時,參數方程也是高考數學理科考查的內容,題目出現在高考試卷的第22題.筆者對新疆2018年至2022年高考數學試卷中有關“坐標系與參數方程”考查的知識點列表(表1)統計如下:
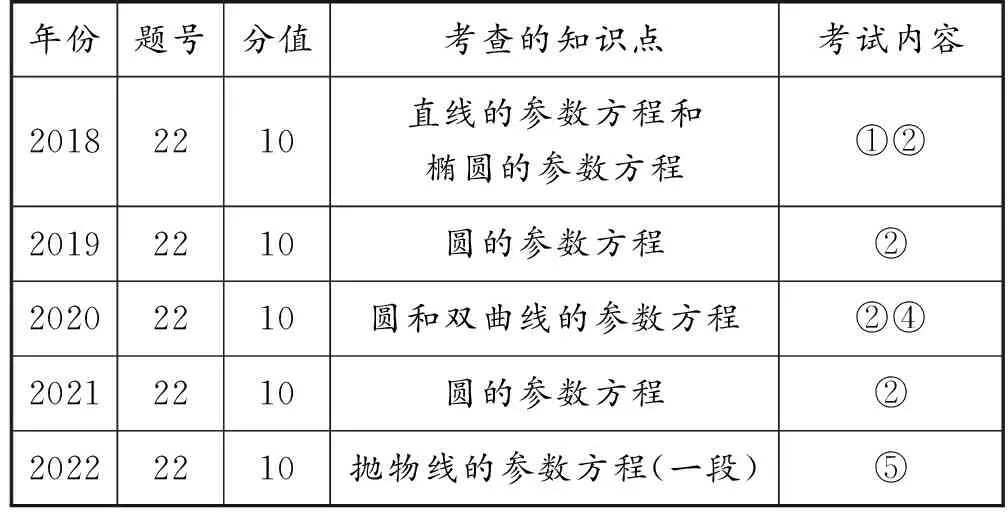
表1
新疆高考所用的試卷為新課標全國卷Ⅱ或全國乙卷.筆者研究了近五年的高考理科數學試卷第22題(1)(2),其中(1)考查曲線(包括直線)的參數方程,(2)考查曲線的極坐標方程.通過2018年至2022年五年的考卷,分析試卷的命題方向及其解題類型與方法,旨在為加高三第一輪復習提供幫助.
2 題型總結
在高三第一輪復習這部分內容時,一方面要了解參數的幾何意義,另一方面還要掌握參數方程的形式及其基本應用.筆者根據自己多年的教學經驗,總結出參數方程的基本應用有如下6種類型,僅供讀者參考.
2.1 類型1:參數方程與普通方程的互化
例1填空(參數方程化為普通方程):
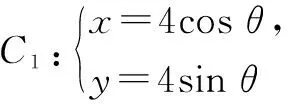
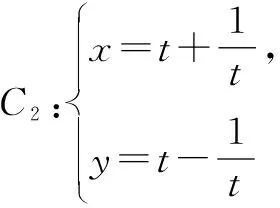
分析:本題為2020年高考第22題的改編,直接消去參數即可得普通方程.
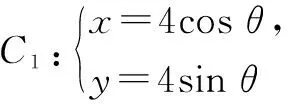
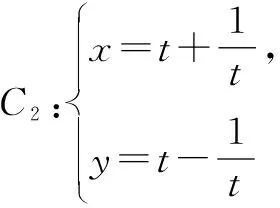
例2把下列的普通方程化為參數方程:
(1)x2+y2=9;
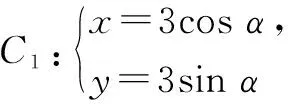
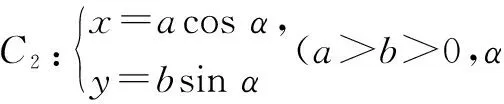
點評:參數方程與普通方程兩種形式的互化體現了等價轉化的數學思想.
2.2 類型2:求直線與曲線的參數方程
例3如圖1,設O為坐標原點,M是圓O:x2+y2=1上的任意一點,過點M作x軸的垂線,垂足為N,試求線段MN中點P的軌跡的參數方程,并指出它是什么曲線.
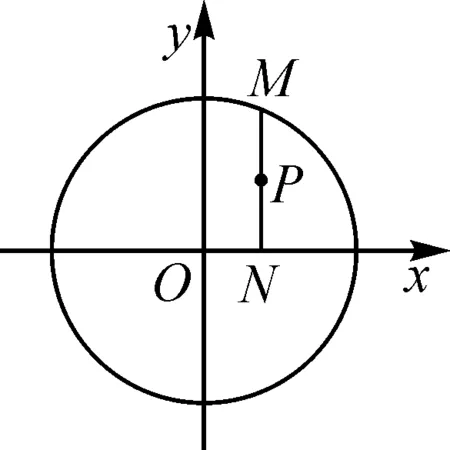
圖1
分析:本題可以利用求曲線方程的“五步法”求出曲線的參數方程.
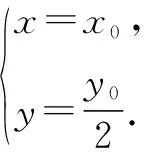
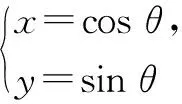
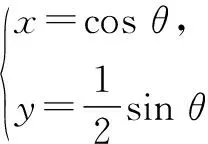
點評:本題是求曲線的參數方程,結合所給的圖形,設出參數θ,建立關于參數θ的方程,體現了數形結合的數學思想.
2.3 類型3:利用參數方程解決函數的最值問題
例4已知實數x,y滿足(x-2)2+(y-1)2=1,試求:(1)S=x+y的最值;(2)T=x2+y2的最值.
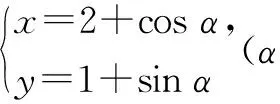
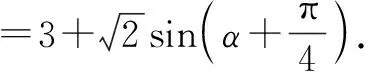
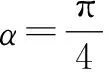
(2)結合(1)中的參數方程,得
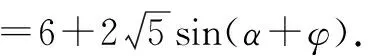
點評:本題是利用圓的參數方程,通過“三角換元”轉化為三角函數的最值問題.這也是我們求最值常用的三角換元法.對于(2)也可以用“幾何法”求解,式子x2+y2的幾何意義是原點到圓(x-2)2+(y-1)2=1上點的距離的平方.
2.4 類型4:利用參數方程解決曲線上的點到直線距離的最值問題
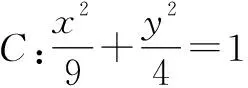
解析:利用橢圓C的參數方程可設點M的坐標為(3cosα,2sinα),則點M到直線l的距離
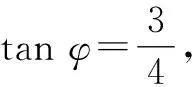
點評:先把橢圓的普通方程化為參數方程,再把點M到直線l的距離轉化為關于參數的三角函數的最值問題.本題也可以采用平移相切法來處理.本題采用三角換元法解題,體現了數學的化歸思想.
2.5 類型5:利用參數方程解決弦長問題
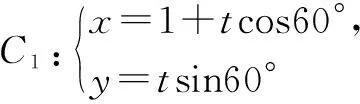
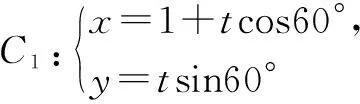
所以,截得的弦長為|t2-t1|=1.
點評:根據參數t的幾何意義,|t|為直線上的點到點(1,0)的距離,可知|t2-t1|為直線被圓截得的弦長.
2.6 類型6:曲線(包括直線)的參數方程的綜合性應用問題
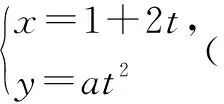
(1)求常數a的值;(2)寫出曲線C的普通方程.
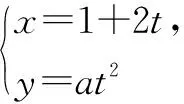
由點M(5,4)在曲線C上,得4×4=a(5-1)2,即a=1.
(2)由(1)知,曲線C的普通方程為(x-1)2=4y.
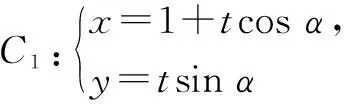
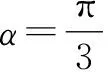
(2)過原點O作直線C1的垂線,垂足為A,P為OA的中點,當角α發生變化時,試求動點P的軌跡.
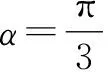
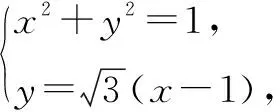
(2)因為C1的普通方程為
xsinα-ycosα-sinα=0,
①
所以過坐標原點且垂直于C1的直線方程為
xcosα+ysinα=0.
②
聯立①②,可得A(sin2α,-sinαcosα).
當角α發生變化時,點P的軌跡的參數方程為
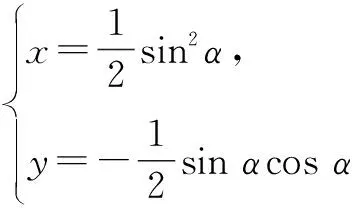
消去參數α,可得點P的軌跡的普通方程
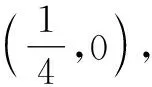
點評:本題考查了直線與圓的參數方程以及直線與圓的位置關系.
3 結束語
本課例列舉了參數方程的六種題型,通過本節課的教學,幫助學生厘清參數方程的題型特征與解題方法,學會分析與思考解參數方程相關問題的通性與通法.本文中根據近五年高考第22題列表統計與分析,幫助老師和學生了解高考有關參數方程命題的方向,另外,通過對這些題型的探究與解析,幫助學生學會分析其他數學難題,拓展參數方程的應用范圍.由于“參數方程”在高考數學中特殊而重要的地位,因此在第一輪復習時,要研究高考命題的難度和類型,從而有針對性地進行第一輪復習,且要注意復習的實效性,切實讓學生弄懂學會,在應對高考或“模考”時,信心滿滿,游刃有余!并在此過程中培養學生的數學運算與邏輯推理等核心數學素養.

