基于數據歸一化原點矩約束最大熵原理的小樣本數據測量不確定度評定
□ 鐘 浩 □ 張為民 □ 謝樹聯 □ 賈子瑋
同濟大學 機械與能源工程學院 上海 201804
1 研究背景
在生產制造中,測量檢驗是重要環節。然而,測量過程中的隨機因素會造成被測量量值具有分散性。測量不確定度是表征被測量量值分散性的非負參數,可以表明測量結果的可信程度,是測量結果不可缺少的參數[1-2]。隨著消費市場對產品的需求向個性化和多樣化轉變,越來越多的企業由大批量生產模式向多品種小批量生產模式轉變。由于生產效率的要求,小批量生產時往往不可能針對特定的尺寸與形位特征進行大量測量,所獲得的測量數據樣本較少,此時需要在小樣本測量數據下進行測量不確定度評定。
最大熵原理是Jaynes[3]提出的,核心思想是在推斷一個隨機變量的概率分布時,僅依靠已知信息,不對未知信息進行主觀假設,由此得到信息熵最大的隨機變量分布,能客觀反映隨機變量的分布情況。最大熵原理被應用到很多領域,并展現出巨大的實際價值和研究意義[4]。在機械制造的測量檢驗環節中,可以利用最大熵原理確定測量樣本數據的概率密度函數,進一步完成測量不確定度的評定[5-8]。
以原點矩為約束的最大熵原理是基本且應用廣泛的最大熵原理,求解概率密度函數的準確性受樣本量大小和原點矩階數影響。樣本量足夠大時,基于更高階的原點矩可以得到更準確的結果。但隨著階數的增加,求解過程越來越復雜,反而使計算結果不準確[9]。因此,選擇更高階的原點矩不能解決小樣本數據下基于原點矩約束最大熵原理求得的測量不確定度不可靠的問題。另一方面,當測量值較大時,基于原點矩約束最大熵原理在優化求解時有數值溢出風險[10-11]。筆者針對經典原點矩約束最大熵原理在小樣本測量數據情況下求出測量不確定度不夠準確可靠,存在數值溢出風險的問題,提出適用于小樣本測量數據的基于數據歸一化原點矩約束最大熵原理的測量不確定度評定方法,并驗證有效性,為基于最大熵原理的測量不確定度評定的研究與應用提供參考。
2 數據歸一化原點矩約束最大熵原理
設測量樣本數據x的樣本區間為[xmin,xmax],對其進行歸一化處理,歸一化處理后的隨機變量為y,區間為[0,1],歸一化公式為:
(1)
根據最大熵原理,隨機變量y唯一的概率密度函數p(y)可由最大熵H(y)確定,即:
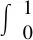
(2)
在原點矩約束條件下,有:
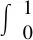
(3)
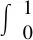
(4)
(5)
式中:mi為i階原點矩,i=1,2,3,…,n。
使用拉格朗日乘子法在熵函數中引入拉格朗日乘子λ0、λ1、…、λn,可得:
(6)
(7)
再由式(3)、式(4)和式(7),可得:
(8)
參數λi方程組為:
(9)
設殘差為ri,有:
(10)
當殘差的二次方和最小時,可以求解出λi的最優解,為:
(11)
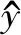
(12)
(13)
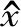
(14)
u=(xmax-xmin)σ
(15)
針對參數λi,可用非線性最小二乘法[14]、爬山搜索算法[6,13]、粒子群算法[15]、遺傳算法[16]等進行優化求解。筆者采用Nelder-Mead算法求解參數λi的最優解,確定測量樣本數據的概率密度函數。
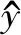
3 數值仿真
在Python軟件中先基于正態分布N(5,0.5)生成10個隨機數,表示加工結果真實值。再基于正態分布N(0,0.1)生成100個隨機數表示測量誤差,每10個為1組,分別與之前10個隨機數進行相加,形成10組數據。仿真隨機數據見表1。
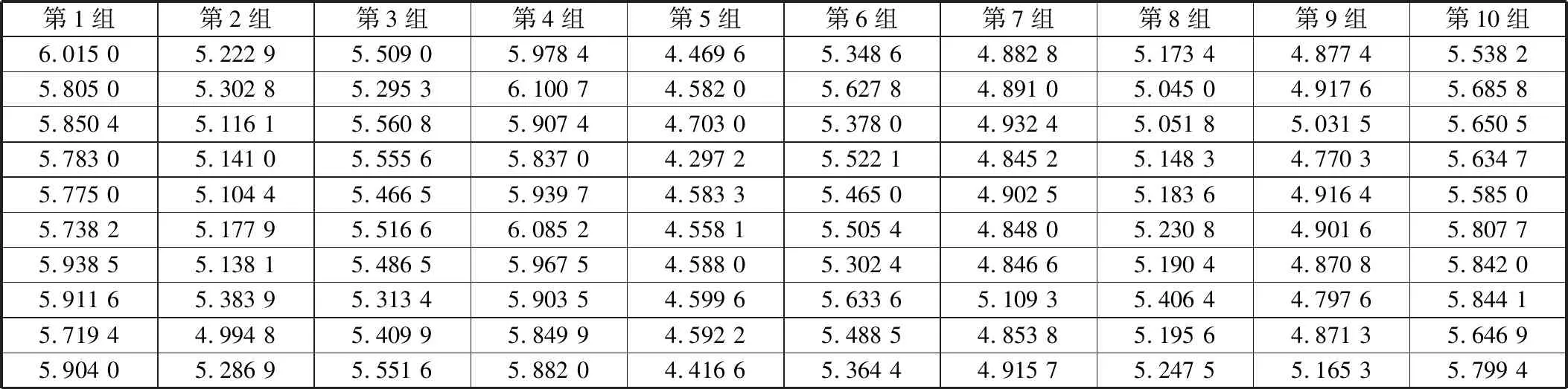
表1 仿真隨機數據
使用數據歸一化原點矩約束最大熵原理,對上述仿真隨機數據進行測量不確定度評定。以第1組數據為例,對數據進行歸一化處理,積分區間為[0,1],選擇3階矩,求得樣本原點矩m1為0.421 6,m2為0.272 9,m3為0.205 4。在Python軟件中編寫計算程序,使用Nelder-Mead算法進行優化求解,設定λ1、λ2、λ3的初始值依次為0.5、0.5、0.1,優化得到最優解λ1為-3.680 4,λ2為3.118 3,λ3為-0.262 2,代入式(8)可得λ0為0.813 2,由此得到歸一化后y的概率密度函數為:
p(y)=exp(0.813 2-3.680 4y+3.118 3y2-
0.262 2y3)
(16)
由式(12)~式(15)求得第1組數據的測量不確定度為0.091 2。以相同方式求出其它組測量不確定度。為進行比較,同時以原點矩約束最大熵原理[13]和概率權重矩約束最大熵原理[17]計算仿真隨機數據的測量不確定度,且同樣選擇3階矩。三種方法計算得到的測量不確定度結果見表2。三種方法計算的測量不確定度散布對比如圖1所示。
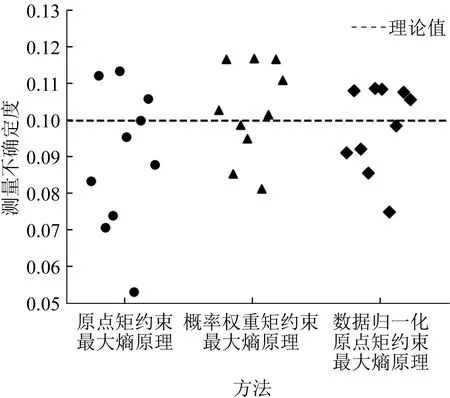
圖1 仿真隨機數據測量不確定度散布對比

表2 仿真隨機數據測量不確定度結果
從圖1中可以明顯看出,基于原點矩約束最大熵原理的評定結果中,有六組數據評定結果小于理論值,有三組數據評定結果大于理論值,整體評定結果分布偏于理論值下方。基于數據歸一化原點矩約束最大熵原理和基于概率權重矩約束最大熵原理的評定結果較均勻地分布在理論值上下,與理論相符。三種方法計算的10組仿真隨機數據的測量不確定度均值及與理論值偏差見表3。數據歸一化原點矩約束最大熵原理與概率權重矩約束最大熵原理一樣,更為接近理論值0.1,與理論值的相對偏差分別僅為1.9%和2.6%,而原點矩約束最大熵原理與理論值的相對偏差則達到了10.4%。三種方法中,所提的數據歸一化原點矩約束最大熵原理表現最佳。由仿真隨機數據的測量不確定度評定結果分析可得,數據歸一化原點矩約束最大熵原理能夠有效提高小樣本測量數據下基于原點矩約束最大熵原理測量不確定度評定的準確性。
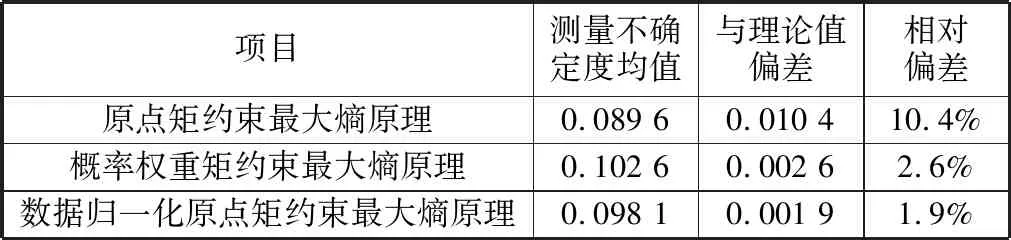
表3 仿真隨機數據測量不確定度均值及與理論值偏差
4 應用案例
以某一小批量閥塊零件為例,檢驗所提基于數據歸一化原點矩約束最大熵原理的測量不確定評定方法的應用效果。使用三坐標測量機進行測量,測量閥塊零件距離圓柱頂端5.5 mm處圓度,如圖2所示。先對一個零件重復測量100次,將其標準差0.61 μm作為理論值。之后分別測量十個閥塊零件的圓度,每個零件重復測量10次,獲得的圓度測量值見表4。

圖2 閥塊零件圓度測量
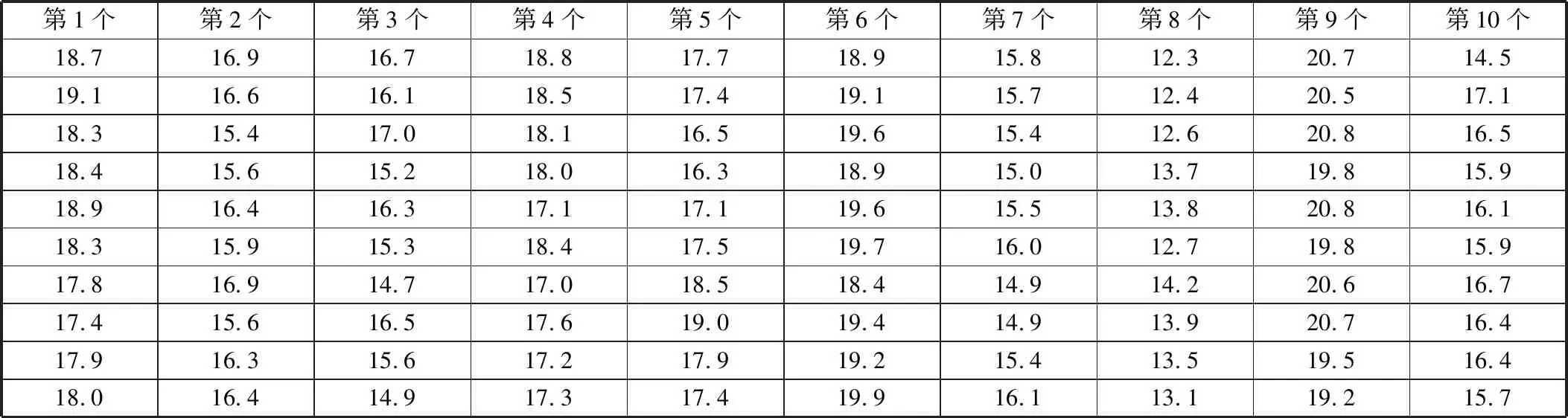
表4 閥塊零件圓度重復測量數據 μm
同樣采用三種方法分別計算閥塊零件圓度重復性測量不確定度,計算結果見表5。三種方法計算的閥塊零件圓度測量不確定度散布對比如圖3所示。

圖3 閥塊零件圓度測量不確定度散布對比

表5 閥塊零件圓度測量不確定度
從圖3中可以明顯看出,基于原點矩約束最大熵原理評定的十個閥塊零件的圓度測量不確定度分布偏于理論值下方,其中有七個閥塊零件的評定結果小于理論值。基于數據歸一化原點矩約束最大熵原理和基于概率權重矩約束最大熵原理的評定結果相對均勻地分布在理論值上下。這與仿真隨機數據的測量不確定度分析結果一致。三種方法計算的十個零件的圓度測量不確定度均值及與理論值偏差見表6。 原點矩約束最大熵原理與理論值0.61 μm相對偏差為14.75%,數據歸一化原點矩約束最大熵原理與理論值相對偏差為3.28%,概率權重矩約束最大熵原理與理論值相對偏差為1.64%。因此,應用案例分析再次證明了在小樣本測量數據下數據歸一化原點矩約束最大熵原理的有效性,能有效提升原點矩約束最大熵原理在小樣本測量數據下的測量不確定度評定的準確性。
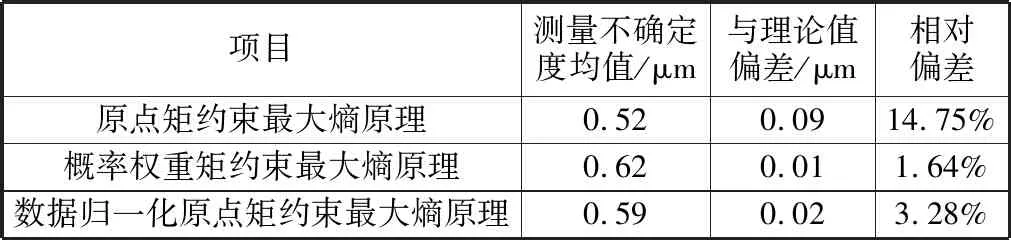
表6 閥塊零件圓度測量不確定度均值及與理論值偏差
5 結束語
筆者針對小樣本測量數據下基于原點矩約束最大熵原理評定的測量不確定度不準確問題,提出適用于小樣本測量數據的基于數據歸一化原點矩約束最大熵原理的測量不確定度評定方法,并進行數值仿真和應用案例驗證。數值仿真與應用案例驗證結果顯示,基于數據歸一化原點矩約束最大熵原理評定的測量不確定度均勻分布在理論值上下。在數值仿真驗證中,10組仿真隨機數據評定結果的均值與理論值的相對誤差僅為1.9%,而原點矩約束最大熵原理與理論值的相對誤差為10.4%。在應用案例驗證圓度測量不確定度評定中,對十個閥塊零件圓度的評定結果與大量重復測量的圓度測量不確定度理論值相比,相對誤差為3.28%,而原點矩約束最大熵原理與理論值的相對誤差為14.75%。由此,在小批量生產的測量檢驗環節中,對于只能獲得小樣本測量數據的情況,與原點矩約束最大熵原理相比,數據歸一化原點矩約束最大熵原理能夠準確有效評定測量不確定度,提高小樣本測量數據下基于原點矩約束最大熵原理測量不確定度評定的可靠性。

