考慮含水量循環滯回變化的非飽和土強度研究

姚科　易磊　郭胤徴　孟鑫　蔡啟航　李幻

摘 要：【目的】探討基質吸力和含水量對非飽和土抗剪強度的影響，總結其變化規律。【方法】基于Bishop非飽和土強度模型和毛細滯回內變量模型的方法，發展了一個考慮含水量循環滯回變化影響的非飽和土強度模型。通過對選取的試驗數據進行驗證分析，發現模型與實際情況吻合。【結果】隨著基質吸力的增加，非飽和土的抗剪強度會增加。當基質吸力達到極大值，即含水量極低時，土體的強度反而減小；隨著含水量的減小，土體的抗剪強度會增大。當非飽和土的含水量達到一定閾值后，土體的抗剪強度反而在一定程度上減小。【結論】以上僅為數值計算結果，其真實性還需要通過物理試驗進行驗證，以便更好地確定模型的適用性。

關鍵詞：非飽和土強度；Bishop模型；工程地質

中圖分類號：TU431? ? ?文獻標志碼：A? ? ?文章編號：1003-5168（2024）06-0100-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.06.020

Study on Strength of Unsaturated Soil Considering Cyclic Hysteretic of Water Content

YAO? Ke YI? Lei GUO Yinzheng MENG Xin CAI Qihang LI Huan

（School of Earth Science and Engineering， North China University of Water Resources and Electric Power， Zhengzhou 450046， China）

Abstract： [Purposes] The influence of matric suction and water content on the shear strength of unsaturated soil was discussed， and its variation rule was summarized. [Methods] Based on the Bishop unsaturated soil strength model and the capillary hysteretic variable model， an unsaturated soil strength model is developed， which considers the influence of cyclic hysteretic change of water content. Through the verification and analysis of the selected test data， it is found that the model is in good agreement with the actual situation. [Findings] With the increase of matric suction， the shear strength of unsaturated soil will increase. However， when the matric suction reaches the maximum value， that is， when the water content is very low， the strength of the soil decreases. In addition， the shear strength of soil increases with the decrease of water content. However， when the moisture content of unsaturated soil reaches a certain threshold， the shear strength of soil decreases to a certain extent. [Conclusions] The above results are only numerical results， and their authenticity needs to be verified through physical tests in order to better determine the applicability of the model.

Keywords： unsaturated soil strength; Bishop model; engineering geology

0 引言

非飽和土具有獨特的力學性質和行為特征，對其開展研究對工程實踐具有重要意義。土水特征曲線（Soil-water characteristic curve，SWCC）是非飽和土力學研究的基礎，它描述了土壤中含水量與吸力之間的關系。通過土水特征曲線，可以確定土壤的吸力-含水量關系，進而推導出土壤的各種力學參數。近些年，國際上土水特征曲線的研究主要集中在曲線的擬合方法和參數的確定。例如：VG模型［1］、Fledlund ＆ Xing模型［2］等。

剪切強度是土體最基本的物理特性之一，它在土體邊坡、基礎穩定性分析、土壓力計算等方面具有十分重要的意義。在此基礎上， Khalili等［3］提出了一種適用于非飽和土壤的有效壓力系數與其本體吸力的關系，并結合試驗資料，得出了相應的計算公式。Ng等［4］提出了雙變量體系。Vanapalli等［5］根據SWCC得到的非飽和土強度公式。盧肇鈞等［6］在試驗中采用了膨脹力的方法，對膨脹土作了相關的試驗。趙成剛等［7］從理論上分析，由于單一或雙重的應力不能很好地描述土壤的實際力學性質，因此，給出了一種適用于非飽和土壤的通用有效應力理論。林鴻州等［8］分析了吸力對非飽和土強度的影響。湯連生［9］提出了將非飽和土中的吸力細化為幾個部分，并提出了吸力與強度的關系式。趙成剛［10］從熱力學角度探討了非飽和土壤的極限狀態，給出了土壤在達到穩態時所需的限制條件。張常光等［11］給出了條狀基礎在主動土壓力、被動土壓力，以及在任何側壓因子下的極限荷載解析解。繆林昌等［12］通過三軸剪切試驗，研究了不同吸力和干密度條件下膨脹土的強度變化規律，得出了其強度與基質吸力呈雙曲形關系。

本研究以Bishop非飽和土強度模型和李幻等［13］的毛細滯回內變量模型為基礎，研究基質吸力和含水量對非飽和土抗剪強度變化的影響，并通過其變化趨勢總結強度隨吸力和含水量的變化規律。同時研究在吸濕、脫濕的不同路徑上，相同基質吸力條件下土體強度不同的現象，以及相同含水量條件下土體強度不同的現象，并解釋其產生機理。

1 Bishop模型與毛細滯回內變量模型的研究

1.1 Bishop非飽和土強度模型

Bishop提出了非飽和土體的有效應力公式，將飽和土的有效應力概念成功應用于非飽和土，這個公式可以用來計算非飽和土體的有效應力。之后結合摩爾—庫倫強度理論，Bishop推導出了非飽和土的抗剪強度模型［14］如式（1），該模型在非飽和土的研究中得到了廣泛應用。

1.2 毛細滯回內變量模型

毛細滯回內變量模型是韋昌富等建立起來的。該模型可以描述非飽和土的SWCC高階掃描線的基質吸力和含水量之間的變化規律。模型的主要公式如式（2）。

2 考慮含水量循環滯回變化的非飽和土強度模型

2.1 模型簡介

基于Bishop強度公式和毛細滯回內變量模型，發展了一個考慮含水量循環滯回變化影響的非飽和土強度模型。控制土體在吸濕、脫濕不同路徑下，土體的強度分別在相同基質吸力和相同含水量條件下不同的現象，并對非飽和土強度的變化規律進行探討。非飽和土的抗剪強度由兩個主要因素決定：一是土體的飽和強度，二是基質吸力引起的強度。因此，在非飽和土的力學行為研究中，需要考慮這兩個因素的影響。

2.2 模型計算

某砂土a的材料參數表見表1。基于文獻中的試驗數據，代入計算了某砂土a的SWCC。砂土的有效黏聚力為0，數據中沒有摩擦角和土體飽和強度的數值，但為了更好地模擬，表1中效摩擦角大小和土體飽和強度大小都是根據砂土屬性范圍內的值假定的。

某砂土a的脫濕、吸濕掃描線分別如圖1、圖2所示。其中，SWCC的邊界線包括主脫濕線和主吸濕線，是根據Feng和Fredlund提出的方程描述的；邊界線內部的脫濕掃描線和吸濕掃描線則是根據毛細滯回內變量模型來描述的。

3 基質吸力與含水量對非飽和土抗剪強度的影響

3.1 基質吸力對非飽和土強度的影響

一般來說，隨著基質吸力的增加，非飽和土的抗剪強度會增加。但當基質吸力極大，即含水量極其小時，土體的強度反而減小。砂土a邊界線強度隨基質吸力的變化曲線如圖3所示，砂土a脫濕、吸濕掃描線強度隨基質吸力的變化曲線分別如圖4、圖5所示。由圖3至圖5可知，非飽和土體在脫濕路徑上，土體的強度隨著基質吸力的增大和含水量的減小會增加，而當基質吸力達到某一極大值后，繼續增加反而會導致土體強度減小；在吸濕路徑上，隨著基質吸力的減小，土體的強度呈現先增大后減小的變化趨勢。這種變化與非飽和土強度變化的一般規律相符。

原因分析如下：一方面，增加基質吸力會導致非飽和土的水分含量減少，并增加土體顆粒間的接觸面積，進而提高土體的內摩擦角，從而增強其抗剪強度；另一方面，基質吸力的增加還會使得土壤中的氣體含量增加，氣體的存在會填充土壤顆粒間的空隙，增加土體的密實度，進一步提高抗剪強度。此外，基質吸力的增加還會引起土體內部的吸力應力分布的變化，改變土體內部的應力狀態，從而影響土體的抗剪強度。

相同基質吸力條件下砂土a的抗剪強度對比見表2。由表2可見，非飽和土在不同路徑上，即使基質吸力相同，其強度也會有較大差異。在脫濕過程中的含水量要高于吸濕過程中的含水量，并且在脫濕路徑上的抗剪強度也要高于吸濕路徑上的抗剪強度。這種差異是由非飽和土的基質吸力引起的。因此，在非飽和土的研究中，需要考慮吸濕和脫濕過程對土體強度的影響。

非飽和土的抗剪強度受到含水量的影響。當基質吸力相同時，含水量的不同是導致強度差異的主要原因。較高的含水量會使土體中的孔隙水增多，導致有效應力減小，從而使抗剪強度較低。相反，較低的含水量會減少孔隙水，增加有效應力，提高抗剪強度。因此，在相同基質吸力條件下，非飽和土的抗剪強度增加部分主要由含水量決定。然而，當含水量達到一定閾值后，總的毛細力減小，土體的抗剪強度反而在一定程度上會減小。

3.2 含水量對非飽和土強度的影響

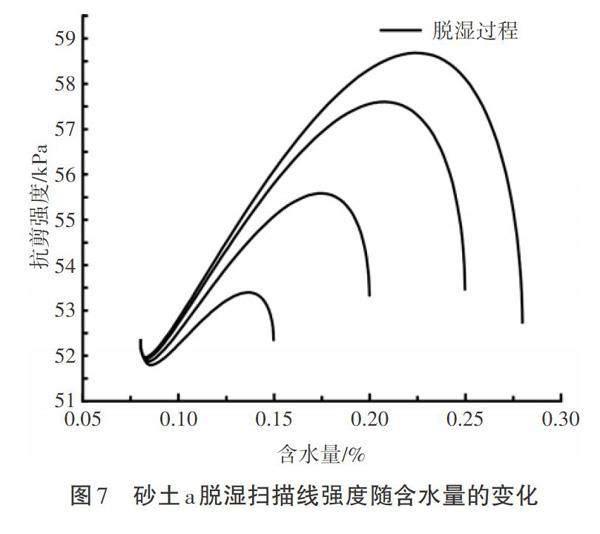
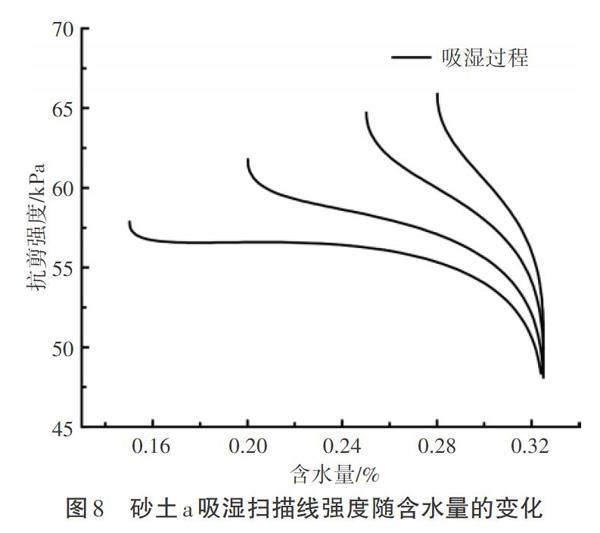
砂土a邊界線上的強度隨含水量的變化曲線如圖6所示，砂土a脫濕、吸濕掃描線強度隨含水量的變化曲線分別如圖7、圖8所示。由圖6至圖8可以看出，非飽和土的抗剪強度呈現出以下規律：隨著含水量的減小，土體的抗剪強度增大；當非飽和土的含水量達到一定閾值后，土粒間總的毛細力減小，土體的抗剪強度反而在一定程度上減小。

原因分析如下：一般來說，隨著含水量的減小，非飽和土的抗剪強度會增加。但是，這種關系并不是簡單的線性關系。在高含水量范圍內，土體中的孔隙水較多，對土體顆粒的支撐作用較弱，使得土體的有效應力減小，從而抗剪強度較低。而在低含水量范圍內，土體中的孔隙水較少，顆粒之間的接觸面積增多，摩擦力增加，使得有效應力增大，從而抗剪強度較大。在中間含水量范圍內，土體的顆粒間結構較松散，摩擦力較低，同時孔隙水的存在減小了有效應力，導致抗剪強度較低。但是，當非飽和土的含水量達到一定閾值后，總的毛細力減小，這就導致土體的抗剪強度在一定程度上反而會減小。

相同含水量條件下，砂土a的抗剪強度對比見表3。由表3可以看出，當含水量相同時，其抗剪強度也并不相同。這是因為在兩種路徑下，雖然其含水量相同，但是水分在土體中的賦存方式并不相同。簡單來說，在含水量相同的條件下，脫濕路徑下非飽和土體中的水分主要分布在較大孔隙中，而吸濕路徑下非飽和土體中的水分會逐漸填充較小孔隙。正是由于水分在土體內分布規律不同，導致即使土體含水量相同，其強度有較大的差異，這一點在土體處于脫濕、吸濕不同路徑上時可以很明顯看到。

出現基質吸力相同條件下，土體產生了非飽和土的強度差異這種情況，主要是由于基質吸力的變化。基質吸力導致土體抗剪強度差異的主要原因是孔隙水分子對土體顆粒之間的影響。當基質吸力較大時，孔隙水分子被吸附在顆粒表面，增加了顆粒間的接觸面積，從而增加了顆粒間的摩擦力，提高了土體的抗剪強度。相反，當基質吸力較小時，孔隙水分子較多，減少了顆粒間的接觸面積，降低了顆粒間的摩擦力，導致土體的抗剪強度降低。因此，基質吸力對土體的抗剪強度產生影響的機制是通過調控孔隙水分子對顆粒間接觸面積和摩擦力的影響。在含水量相同時，基質吸力大小決定了非飽和土的強度差異的主導地位。

4 結論

①本研究基于Bishop非飽和土抗剪強度模型和毛細滯回內變量模型，發展了一個考慮含水量循環滯回變化影響的非飽和土強度模型。該模型用來計算非飽和土在含水量任意變化條件下土體強度的變化規律。

②基質吸力對非飽和土的抗剪強度具有顯著影響。隨著基質吸力的增加，非飽和土的抗剪強度逐漸增大。這種影響主要是由于基質吸力導致土體水分含量減少、氣體含量增加和內部應力狀態的改變。

③含水量對非飽和土抗剪強度具有顯著影響。隨著含水量的減小，非飽和土的抗剪強度逐漸增大，當非飽和土的含水量達到一定閾值后，土粒間總的毛細力減小，非飽和土的抗剪強度反而在一定程度上減小。這種影響主要是由于含水量減小時，土體中的孔隙水較少，土壤顆粒之間的接觸面積增多，導致顆粒之間的摩擦力增加，這會增加土體的有效應力，從而提高了土體的抗剪強度。

④以上僅為數值計算結果，其真實性還需要通過物理試驗進行驗證，以便更好地確定模型的適用性。

參考文獻：

［1］VAN GENUCHTEN M T. A close-form equation for predicting the hydraulic conductivity of unsaturated soils ［J］. Soil Science Society of America Journal，1980，44：892-898.

［2］FREDLUND D G，XING A. Equations for the soil-water characteristic curve ［J］. Canadian Geotechnical Journal，1994，31（4）：521-532.

［3］KHALILI N，KHABBAZ M. A unique relationship of chi for the determination of the shear strength of unsaturated soils ［J］. Geotechnique，1998，48（5）：681-687.

［4］NG C W W，PANG Y W. Influence of stress state on soil-water characteristics and slope stability ［J］. Journal of Geotechnical and Geo environmental Engineering，2000，126（2）：157-166.

［5］VANAPALLI S K，FREDLUND D G，PUFAHL D E，et al. Model for the prediction of shear strength with respect to soil suction ［J］. Canadian Geotechnical Journal，1996，33（3）.

［6］盧肇鈞，吳肖茗，孫玉珍，等.膨脹力在非飽和土強度理論中的作用［J］. 巖土工程學報，1997，19（5） ：20-27.

［7］趙成剛，蔡國慶.非飽和土廣義有效應力原理［J］. 巖土力學，2009，30（11）：3232-3236.

［8］林鴻州，李廣信，于玉貞，等.基質吸力對非飽和土抗剪強度的影響［J］. 巖土力學，2007（9）：1931-1936.

［9］湯連生.從粒間吸力特性再認識非飽和土抗剪強度理論［J］. 巖土工程學報，2001（4）：412-417.

［10］趙成剛.熱動力學的穩態與非飽和土的臨界狀態［J］. 巖土工程學報，2012，34（4）：730-733.

［11］張常光，胡云世，趙均海.平面應變條件下非飽和土抗剪強度統一解及應用［J］.巖土工程學報，2011，33（1）：32-37.

［12］繆林昌，崔穎，陳可君，等.非飽和重塑膨脹土的強度試驗研究［J］. 巖土工程學報，2006（2）：274-276.

［13］李幻，韋昌富，顏榮濤，等.非飽和土毛細滯回內變量模型的修正［J］. 巖土力學，2010，31 （12）：3721-3726.

［14］ BISHOP A W，BLIGHT G E. Some aspects of effective stress in saturated and partly saturated soils ［J］.Geotechnique，1963，13（3）：177-197.

［15］ POULOVASSILIS A. Hysteresis of pore water in granular porous bodies ［J］. Soil Science，1970，109（1）：5-12.