雙種群協同演化的改進蜜獾算法

柴巖 王如新 任生

摘 要：針對蜜獾算法存在的局部搜索能力不足、易陷入局部最優值等問題，提出一種雙種群協同演化的改進蜜獾算法。在初始化階段采用Cubic混沌映射對種群進行初始化，擴大可行解的搜索范圍并提高種群的分布均衡性；引入融合黏菌算法和蜜獾算法的雙種群優化機制，依托兩者的更新優勢協同推進個體逼近目標位置，進而提高整個算法的搜索效率和優化性能；采用柯西隨機反向擾動策略對蜜獾種群最優位置進行擾動，以提高算法跳出局部最優的能力。通過評估單一策略的改進有效性實驗、與七種對比算法的不同高維實驗以及Wilcoxon秩和檢驗，結果表明該算法具有良好的收斂精度和求解速度。最后將改進算法應用于壓縮彈簧設計和壓力容器設計問題，進一步驗證了改進策略的有效性及該算法的工程實用性。

關鍵詞：蜜獾算法； Cubic混沌映射； 雙種群協同優化； 柯西隨機反向擾動； 工程應用

中圖分類號：TP301.6?? 文獻標志碼：A

文章編號：1001-3695（2024）03-014-0736-10

doi：10.19734/j.issn.1001-3695.2023.05.0293

Improved honey badger algorithm for dual population collaborative evolution

Chai Yan， Wang Ruxin， Ren Sheng

（College of Science， Liaoning Technical University， Fuxin Liaoning 125105， China）

Abstract：To address the weaknesses of the honey badger algorithm， specifically its limited capacity for local search and susceptibility to local optima， this paper proposed an enhanced version based on coevolution with two populations. This approach used Cubic chaotic mapping to initialize the population， thereby expanding the search space and improving its distribution. Moreover， it introduced a dual-population optimization mechanism that combined the slime mold algorithm with the honey ba-dger algorithm. By leveraging the strengths of both methods， the individuals could more effectively hone-in on the target location， resulting in improved search efficiency and optimization performance. To further improve the algorithms ability to escape local optima， it employed a Cauchy random reverse perturbation strategy to disturb the optimal position of the honey badger population. By means of the experiment of improving the effectiveness of a single strategy， different high-dimensional experiments with seven other algorithms and Wilcoxon rank-sum tests， experimental results demonstrate that the proposed algorithm has high convergence accuracy and fast solving times. Finally， this paper applied the improved algorithm to the design of compression springs and pressure vessels， which further confirmed the efficacy of improved strategy and the practical utility of the algorithm.

Key words：honey badger algorithm; Cubic chaotic mapping; double population cooperative optimization; Cauchy random reverse perturbation; engineering application

0 引言

隨著科技的不斷創新和發展，眾多工程問題需要進一步優化求解。由于傳統優化方法，如牛頓法［1］、梯度下降法［2］等存在易陷入局部最優、增加時間復雜度等問題，現已無法滿足實際需求。元啟發式算法利用仿生學或物理學現象來進行優化求解，因其框架簡單且搜索策略具有較好的可擴展性和魯棒性，所以在解決工程優化問題方面具有很大優勢。目前元啟發式算法主要包括模擬退火算法（simulated annealing，SA）［3］、禁忌搜索算法（taboo search，TS）［4］、粒子群優化算法（particle swarm optimization，PSO）［5］、灰狼優化算法（grey wolf optimizer，GWO）［6］、正余弦算法（sine cosine algorithm，SCA）［7］、變色龍算法（chameleon swarm algorithm，CSA）［8］、野狗優化算法（dingo optimization algorithm，DOA）［9］、黏菌算法（slime mould algorithm，SMA）［10］等。其中群體智能算法采用多個個體并行搜索的方式來實現分布式計算，適合處理大規模數據和高維問題且具有較好的魯棒性，在實際優化問題中具有一定優勢。

群體智能優化算法面臨的挑戰主要包括種群多樣性不足和收斂速度問題。為應對這些挑戰，學者們進行了相關研究并提出了多種解決方案：

a）在種群初始化階段，提出使用混沌映射，如Chebyshev［11］、tent［12］等來遍歷整個解空間，以增加種群的多樣性；同時，應用Halton序列［13］、Sobol序列［14］等方法調控種群的空間分布；此外采用反向學習策略［15］也可以提高種群的多樣性。

b）在位置更新階段，董奕含等人［16］提出了局部-全局信息共享策略，通過共享全局最優解的信息，使算法根據當前位置附近的信息進行更新和調整，然而該策略存在不同個體之間共享信息增加溝通成本的問題；Wang等人［17］采用領導者-跟隨者策略，其中跟隨者會根據領導者的位置和行為進行更新，但是跟隨者受領導者局限性的影響，可能無法得到理想的結果。

c）在最優位置處，有學者利用柯西變異因子［18］對最優位置進行擾動，然而這樣會增加搜索空間的復雜性，增加算法迭代次數；其次，階梯步進策略［19］可以保證當前優勢個體加快向全局最優前進的趨勢，但會導致過早收斂；此外，采用黃金萊維飛行策略和t-分布擾動策略來共同改進發現者位置的更新，其中動態調整參數的設置相比起簡單且固定的參數設置方法需要更多的計算量。

雙種群協同策略［20］相較于以上策略，在位置更新和確定最優位置處實現更高效的優化。一方面，兩個種群之間的信息交流提供了種群間的合作機制，可以獲得更好的解；另一方面，種群之間的競爭可以通過個體的適應度評估來加快進化進程，使種群更快地收斂到全局最優解。本文提出一種雙種群協同演化的改進蜜獾算法（improved honey badger algorithm for dual population collaborative evolution，DPHBA）。首先引入Cubic混沌映射策略，Cubic混沌映射具有良好的隨機性和廣泛的分布性，能夠有效提高算法的全局搜索能力；其次，將黏菌算法融合到蜜獾算法中，不同種群分別進行適應性調整，通過協同共享和競爭可以提高算法的搜索能力，并加速收斂速度；最后，引入柯西隨機反向擾動策略，有效避免算法陷入局部最優解，并提高了全局搜索的效果。通過四組數值實驗以及兩個工程應用問題驗證了DPHBA的尋優精度、收斂速度、穩定性均取得較大提升。

1 蜜獾算法

蜜獾算法（honey badger algorithm，HBA）是Hashim等人［21］提出的一種新型群智能優化算法，它以模仿蜜獾的覓食行為為基礎，旨在模擬蜜獾的兩種不同捕食行為，即挖掘和采蜜。前者依靠嗅覺以確定最佳的捕獲地點，從而實現最佳的捕獲效果；后者則依靠導蜜鳥的指引來捕獲更多的獵物。

1.1 強度

蜜獾根據氣味去尋找食物，獵物氣味強度越大，表示距離蜜獾越近，搜索加速。強度的定義為

3.2 雙種群協同優化機制

在蜜獾算法中，單一搜索模式限制了種群的搜索范圍，并且易發生早熟收斂的現象，主要是由于個體在尋優過程中僅向最優個體進行學習，一旦發現當前最優個體，所有的蜜獾都會向該方向搜索，導致算法探索的領域變小，難以找到更廣闊的搜索空間中潛在的最優解，從而削弱了算法的全局尋優能力。

由于黏菌算法和蜜獾算法產生新個體的方式不同，決定了它們在尋優時的效果也不同，黏菌算法對多峰函數和高維函數的搜索能力較強，蜜獾算法對連續函數和離散函數的搜索能力較強，兩者皆能夠在較短的時間內找到全局最優解。所以本文將其各自優勢相融合，提出了一種雙種群協同優化機制，將種群劃分為兩部分。第一部分采用黏菌算法更新個體位置，第二部分采用蜜獾算法更新個體位置。該算法通過同時演化兩個種群，不僅能夠維持種群的多樣性，還能夠提高算法的收斂速度。在計算復雜度可承受的情況下，該算法具有較強的全局尋優能力。在更新過程中，個體之間相互交換信息、學習經驗，使得全局最優解更容易被搜索到，進而提高算法的搜索效率和準確度。個體之間不僅有合作，還存在一定的競爭關系，以促進算法更好地演化。種群之間的競爭主要表現在個體的選擇上，每次更新結束后，僅保留適應度最好的個體，并將其作為下一次迭代的最優個體，其中最優個體可能來自于前者，也可能來自于后者。種群之間會相互影響來避免算法陷入局部最優解，使得搜索空間更加廣闊，持續保留適應度較高的個體，并更快地逼近全局最優解。

雙種群協同優化機制的偽代碼如下所示。

3.3 柯西隨機反向擾動策略

為了增強算法在局部尋優時的多樣性，同時提高種群逼近最優位置的速度，本文引入了柯西隨機反向擾動策略來交互擾動當前最優解，以增加搜索空間的多樣性和隨機性。具體來說，在種群尋優的過程中，會通過隨機概率發生柯西學習變異和隨機反向學習的交互擾動產生新的擾動解進行后續搜索，從而避免算法陷入局部最優解，并保證了算法的全局搜索能力。

柯西變異［18］具有突變幅度大、保持種群多樣性和適應不同問題的特性，從而能夠防止種群過早陷入局部最優解，并且縮短到達最優位置的時間。因此，將柯西變異算子引入HBA算法中，利用其強大的擾動能力來調控當前最優解。具體表達式如下：

3.5 時間復雜度

時間復雜度是評估算法優劣的重要指標之一，它反映了算法所需的計算資源，通常以輸入規模為函數的增長率來衡量。本文將對HBA和DPHBA的時間復雜度進行比較分析。

在HBA中，假設種群規模為N，搜索維度為D，最大迭代次數為T，適應度函數為f（x）。設在種群初始化階段的時間復雜度為O（N），更新種群位置的時間復雜度為O（TN），局部搜索階段的時間復雜度為O（TND）。標準HBA算法的時間復雜度為O（N）+O（TN）+O（TND）=O（TND）。

基于本文策略改進的 DPHBA，引入Cubic混沌映射初始化種群，未對全局探索階段的更新公式進行改進，所以此階段時間復雜度為O（N）。在全局搜索階段引入雙種群協同優化機制，此方法可以在全局搜索階段中起到加速收斂和提高全局最優解發現概率的作用，只是改變了種群的分配和算法的執行方式，并沒有改變算法本身的復雜度，此階段的時間復雜度為O（TN）。引入柯西隨機反向擾動策略中執行貪婪原則增加的O（T）計算量在同數量級下變化，其余環節復雜度同HBA算法，所以該階段時間復雜度為O（TND）。所以，DPHBA 總的時間復雜度為O（N）+O（TN）+O（TND）=O（TND）。

綜上所述，本文算法與標準的HBA算法的時間復雜度一致，改進后的算法并沒有使原算法的運行時間增加。

4 仿真實驗與結果分析

4.1 實驗設計與結果分析

為檢驗DPHBA求解性能的優越性，共設計了四組實驗：實驗1探究各策略對HBA性能改進的有效性；實驗2是在不同高維情形下與智能算法進行對比，驗證了DPHBA優越的尋優精度和優良的收斂速度；實驗3是不同高維情形下DPHBA與智能算法收斂曲線對比分析；實驗4是Wilcoxon秩和檢驗。使用20個標準測試函數對DPHBA進行性能測試。通過使用單峰測試函數F1～F6評估算法的局部性能，并確定它的收斂速度；使用多峰測試函數F7～F11評估算法的全局搜索能力以及跳出局部性能；F12～F20是固定維測試函數，可用于評估算法平衡探索與開發能力之間的表現。通過以上三種不同的測試函數對算法的求解和開發能力進行有效的評估。

為保證仿真實驗控制變量原則，本文使用的所有算法種群數設置為N=30，最大迭代次數T=500，單峰和多峰函數D=30/100/500/1000。為避免單次實驗運行的隨機性造成的誤差，將每組實驗迭代運行30次，以30次統計結果的平均值（mean）、標準差（std）、最小值（min）、最大值（max）作為評價指標。基準測試函數具體信息如表1所示，各算法的參數設置如表2所示。

4.2 不同策略的改進有效性分析

為驗證三種改進策略對蜜獾算法性能提升的有效性，本文設置僅融合Cubic混沌映射策略的改進蜜獾算法為HBA-1，僅融合黏菌算法的改進蜜獾算法為HBA-2，僅融合柯西隨機反向擾動策略的改進蜜獾算法為HBA-3。實驗參數設置同4.1節，并對基準測試函數進行30次尋優處理，其結果的平均值、標準差、最小值、最大值對比如表3所示，表中加粗數字表示每個函數各指標的最優值。

由表3可知，本文提出的Cubic混沌映射初始化種群、雙種群協同優化機制、柯西隨機反向擾動策略對標準蜜獾算法的尋優性能提升均有一定幫助，并且有利于提升種群整體質量。

HBA-1在各測試函數上的表現良好，其中在函數F1～F3上精度提高了10個數量級，且在復雜多峰函數和固定維度函數上的表現更優于簡單的單峰函數；在函數F7、F9上各項指標均達到了最優值，體現出了Cubic混沌映射生成的隨機序列具有高度的隨機性；在函數F12上各指標達到理論最優值，可以幫助算法跳出局部最優解，從而更快地收斂到全局最優解；在函數F13～F20上最小值達到理論最優值，說明HBA-1具有更高的搜索效率和更快的收斂速度。

HBA-2的指標值在標準HBA的基礎上提升多至數百個單位，且相對于HBA-1、HBA-3，其精度優勢突出。在函數F1和F3上達到了理論最優值，這表明采用融合黏菌算法的蜜獾算法提升了HBA的全局搜索性能，且符合在前期主要進行全局探索、在后期則主要進行局部開發的優化規律；在函數F4上HBA-2的標準差達到理論最優值，意味著算法搜索結果的波動性較小，反映了HBA-2相對于標準HBA算法的搜索結果的穩定性和可靠性更佳;在函數F7～F9上達到理論最優值，說明HBA-2相對于標準HBA有著更好的全局搜索能力和避免局部最優的能力；在函數F12～F20上HBA-2的最小值達到理論最優值，說明HBA-2具有更高的搜索效率和更快的收斂速度；在函數F15～F20上HBA-2的最大值優于其他對比算法，說明雙種群協調機制具有多樣性并行搜索和分布式求解的特點，在尋找最優解時具有較快的收斂速度。同時，HBA-2與DPHBA的收斂精度相對接近，雙種群協調機制能夠有效地避免算法陷入局部最優解，從而增強了算法的魯棒性和可靠性，也證明了該策略在算法精度提高中有著顯著貢獻。

HBA-3 相較標準HBA的尋優能力明顯增強，在函數F1、F3、F5上標準差達到最優值，在函數F7～F9上各項指標均達到理論最優值，同時在函數F13～F20上最小值達到理論最優值，說明HBA-3具有更好的魯棒性和泛化能力，同時具有較強的搜索能力和潛力。證實了柯西隨機反向擾動策略在算法協調全局與局部搜索能力中的重要作用，以幫助更好地預測改進算法在實際應用中的表現，反映出利用柯西隨機反向擾動策略對提升算法尋優有著積極影響。

DPHBA的指標值在各基準測試函數上均優于HBA，特別地，在函數F1～F4、F7～F11以及F14、F15、F18～F20上，DPHBA均可收斂到全局最優值，說明可以在最短時間內找到多數單多峰函數和固定維函數的最小值，并將其收斂到0點。同時說明DPHBA具有最優的收斂精度和魯棒性，從而綜合證明了三種改進策略對標準HBA算法的改進有效。

4.3 不同算法的尋優精度分析

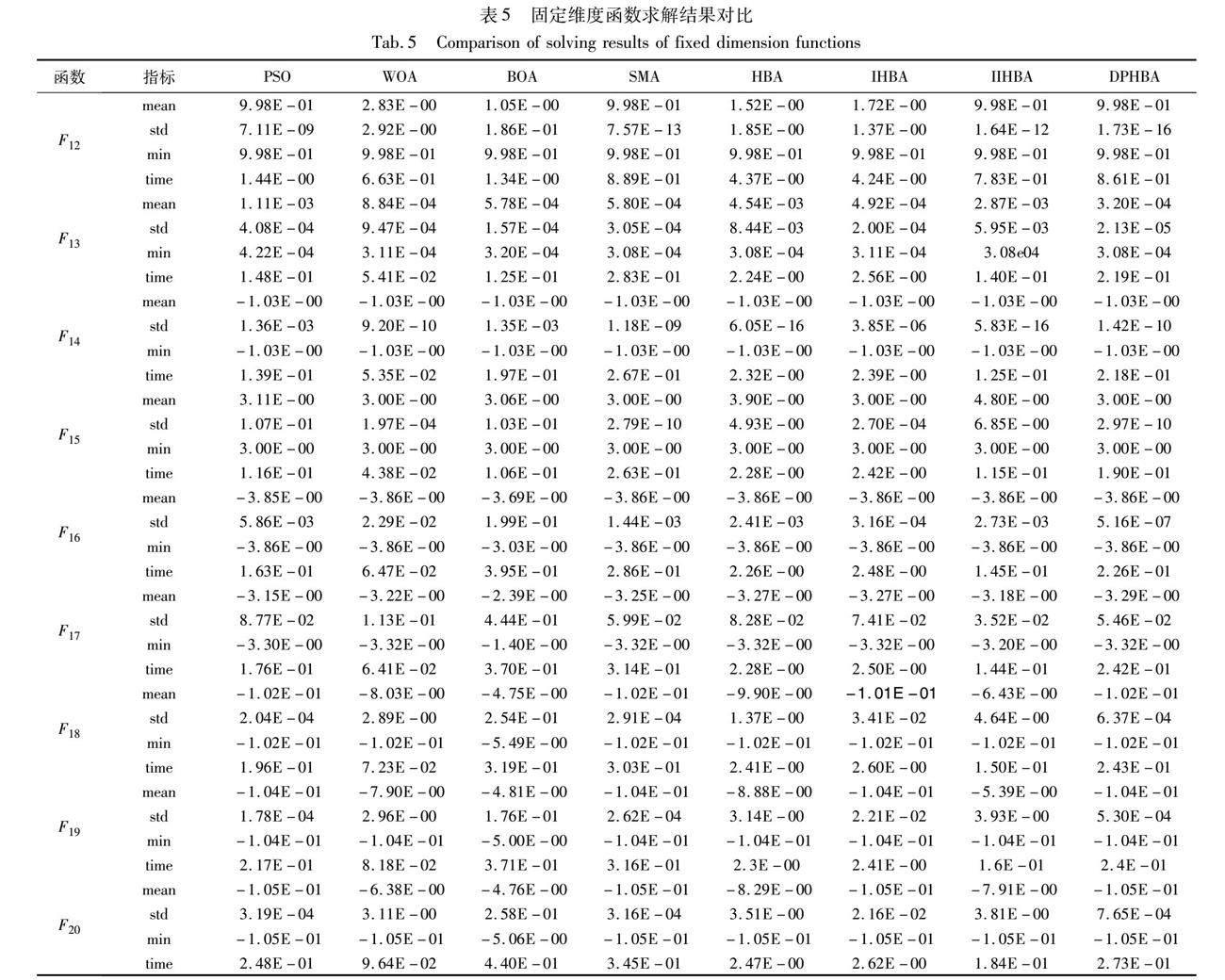
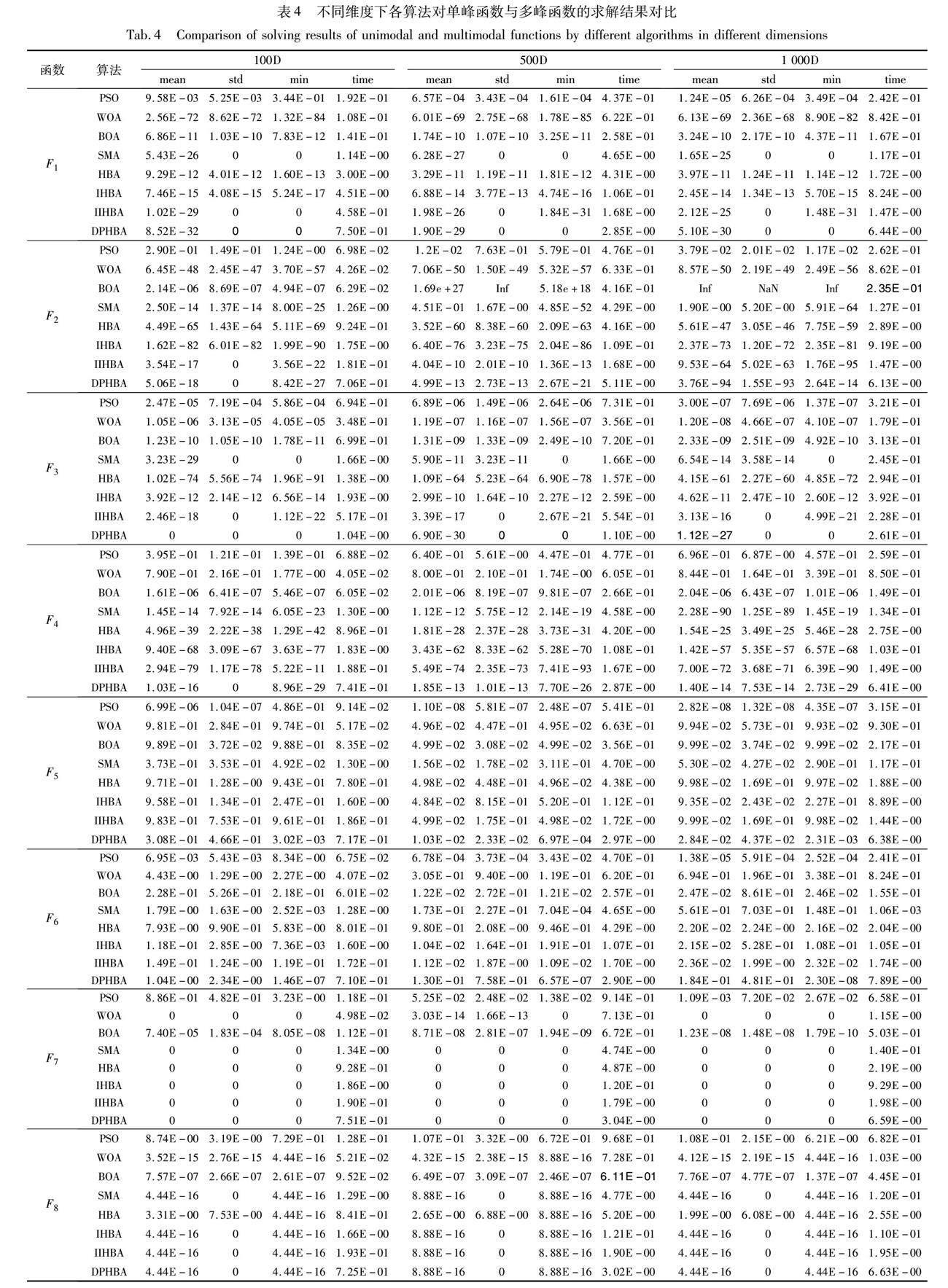
為驗證DPHBA優越的尋優性能，對比分析DPHBA與PSO、WOA［27］、BOA［28］、SMA、HBA、IHBA［11］、IIHBA［18］在測試函數上的尋優情況。實驗種群規模N和最大迭代次數T分別為30、500，單峰、多峰測試函數維度分別設置為100、500、1 000，固定維度函數的維度參照表1，各算法的其他參數設置同原文獻。30次獨立實驗的單、多峰測試函數結果如表4所示，固定維度函數結果如表5所示。

縱向分析表4可知，DPHBA相對于其他七種對比算法各項評價指標均表現最優，甚至在單峰測試函數上30次獨立實驗的平均最優值指標均已經高出其他對比算法數十個乃至上百個數量級，其中在函數F1～F4上，DPHBA的各項指標均達到理論最優值，反映了本文算法優異的收斂精度和良好的穩定性；對于單峰函數F5和F6，DPHBA只有標準差未能達到最優值，但仍優于對比算法，并在平均收斂精度方面高于HBA。對于復雜多峰測試函數，其解空間通常非常大且充滿峰值和局部最小值，DPHBA的尋優能力同樣突出。其中，在函數F7～F11上各項指標均達到理論最優值；對于多峰函數F10和F11，DPHBA雖未達到理論最優值，但是各項指標均已經高出其他對比算法數個數量級。說明DPHBA能夠有效地搜索整個空間，并在其中快速找到全局最優解而不會被卡在局部最優解中。

橫向分析表4可知，當函數的維度增加時，算法的搜索精度也會相應地減少，這是由于維度的擴大會導致種群的搜索范圍擴大，從而影響算法的搜索準確性。但無論在100 D、500 D還是1000 D的高維實驗中，DPHBA受維度升高的影響最小，仍然具有明顯的精度優勢，特別是在求解函數F1～F4、F7、F9時各項指標皆為理論最小值，始終保持各項指標最優的情形，對其他單峰和多峰函數尋優時的平均收斂精度也仍優于對比算法，表明DPHBA擁有更強的尋優能力，證明了DPHBA卓越的尋優競爭力和優異的高維問題適用性，并且在高維標準測試函數上表現出較強的魯棒性。

表5中，對于固定維度測試函數，DPHBA基本都能收斂到理論值附近，尤其在測試函數F12、F13、F16上各項指標表現最優，且在各函數上的最小值表現最佳，高出標準HBA數個數量級，表明DPHBA具有較強的搜索能力和潛力，在解決該測試函數問題時更有效或更準確，并提供了可能獲得更優解決方案的機會。在函數F12、F13、F16上DPHBA的標準差較對比算法表現更好，意味著算法搜索結果的波動性較小，反映了DPHBA搜索結果的穩定性和可靠性，并且說明DPHBA相較于標準HBA具有更好的全局搜索能力和收斂性。

分析表4可知，100 D中WOA的平均運行時間最短，500 D和1000 D中BOA的平均運行時間最短。分析表5可知，WOA的平均運行時間最短，這是由于WOA和BOA結構簡單，其中WOA主要包含更新“引領者”位置和更新“隨從者”位置兩個步驟，這種簡單的結構使得算法減少了計算的復雜性，從而降低了運行時間；同時BOA控制參數少且易于實現，能夠加速搜索過程并減少搜索空間，以快速收斂到較優解從而減少運行時間。而本文提出的DPHBA相較原始HBA能夠在一定程度上減少運行時間。

4.4 不同算法的收斂曲線分析

為更加直觀地觀測各算法的收斂速度、尋優穩定性和局部最優逃逸能力等情況，對各算法的收斂情況進行可視化，在D=100情況下的10個單多峰函數和2個固定維度函數獨立運行30次的收斂曲線對比如圖3所示。其中單峰函數選用F1、F3、F4、F5、F6，多峰函數選用F9、F10、F11、F12、F13，固定維度函數選用F14、F18。

從圖3可以看出，相較于對比算法，DPHBA的迭代趨勢表現更優，并且能夠以更快的收斂速度實現優化研究。由圖3（a）～（c）可見，DPHBA收斂曲線大致呈現冪函數下降，表明DPHBA在單峰函數上以勻速或勻加速進行迭代搜索，表現出強健的搜索穩定性，且算法的收斂速度較標準HBA增快了數倍，其效果源自于引入的柯西隨機反向擾動策略，其目的是以當前解為基礎，對當前最優解進行擾動處理并進行自適應調控，加速了算法收斂效率；同時圖3（d）（e）在迭代次數超過1/2就可以有效地捕捉到多峰函數的全局最佳解，遠遠超過其他算法，從而使得求解多峰函數變得更加容易、有效。各算法在求解多峰函數時，面對復雜的多極值測試函數，雙種群協同優化機制對算法的擾動成功率大大提升，特別是在函數F10、F12、F13上的擾動效果非常明顯，使得算法快速收斂到函數理論值附近。圖3（a）為求解固定函數的平均收斂曲線，各算法均出現了不同程度的停滯現象，而DPHBA具有顯著的優勢，不僅可以有效克服局部極值區的限制迅速從初始階段開始搜索，而且在最終階段的收斂精度也遠遠超過其他算法，表明其具備卓越的全局搜索能力。

綜上所述，不同算法在各測試函數上的動態尋優進程不同且以DPHBA的尋優性能和收斂速度表現最優。

4.5 Wilcoxon秩和檢驗

選取11個維度D=100的單峰和多峰函數以及9個固定維度函數進行Wilcoxon秩和檢驗，進一步比較DPHBA與對比算法的運行效果。其中，顯著性水平設置為0.05，將所有算法的結果運行30次。當檢驗的p＞0.05時，說明兩種算法的運行結果沒有顯著差異；否則，兩種算法運行結果存在顯著差異。表6為DPHBA與對比算法的Wilcoxon秩和檢驗結果。其中：“NaN”表示無法進行顯著性差異判 ，“+/=/-”表示DPHBA和對比算法之間性能的“優于/相當/劣于”。由表6可以看出，絕大多數的p都遠遠小于0.05，可以證明經過對DPHBA的優化，其結果表現出了顯著的優勢，且其統計學意義遠遠超出了其他對比算法。實驗表明，本文提出的雙種群協同演化的改進蜜獾算法的收斂速度、求解精度和魯棒性都有明顯提升。

5 DPHBA算法的工程應用分析

為驗證DPHBA在實際工程應用中的性能，選取了壓縮彈簧設計和壓力容器設計兩種經典的工程優化問題，并且與其他七種算法進行對比，證明了DPHBA在實際工程應用的優越性以及前景。實驗參數設置種群規模為30，最大迭代次數為500，獨立運行30次。

5.1 壓縮彈簧設計問題

壓縮彈簧設計是最小約束優化問題，其目的主要是減輕彈簧的重量。該優化問題根據最小撓度、剪切應力、振蕩頻率以及外徑限制四個約束條件來設計三個變量，即彈簧金屬絲直徑d（x1）、彈簧圈平均直徑D（x2）以及彈簧有效圈數N（x3）。

該問題的數學描述如下所示。

目標函數：

f（x）=（x3+2）x2x21

決策變量取值范圍：

0.05≤x1≤20.25≤x2≤1.32≤x3≤15

約束條件：

g1（x）=1-x32x371875x41≤0g2（x）=4x22-x1x212566（x2x31-x41）+15108x21-1≤0g3（x）=1-140.45x1x22x3≤0g4（x）=x1+x21.5-1≤0

表7列出了DPHBA與對比算法求解壓縮彈簧設計問題的實驗結果，其中加粗字體表示最優值。

根據表7的數據，DPHBA的平均值、最優值、最小值和最大值均為最低，表明本文提出的改進策略比HBA具有更強的搜索能力，為實際應用提供了可靠依據，可以有效地解決壓縮彈簧設計問題，從而證明了DPHBA在解決這類工程問題方面表現出色。

圖4展示了各算法的收斂曲線，可以看到DPHBA的收斂速度和尋優精度明顯優于其他算法， 并且在算法初期的全局搜索能力和后期的局部搜索能力上均具有明顯優勢。與HBA相比，DPHBA由于引入柯西變異，種群跳出局部最優能力增強，引入雙種群協同優化機制，算法的尋優速度大幅度增加。通過對收斂曲線的分析，DPHBA在很大程度上改善了HBA的缺陷，并且提升了尋優精度，在維持原有的優勢下提升了算法的性能。

5.2 壓力容器設計問題

壓力容器設計是經典的工程優化問題，通過降低壓力容器的耗材來降低控制工程成本，其中四個設計變量分別為外殼厚度Ts（x3）、封頭厚度Th（x4）、內半徑R（x1）以及容器長度L（x2，不包括頭部），其中Ts和Th為0.625的整數倍，R和L為連續變量。具體數學模型如下。

目標函數：

min f（x）=0.6224x1x3x4+1.7781x2x23+3.1661x21x4+19.84x21x3

約束條件：

g1（x）=-x1+0.0193x3≤0g2（x）=-x2+0.00954x3≤0g3（x）=-πx23x4-43πx23+1296000≤0g4（x）=x4-240≤0

邊界約束：

0≤x1≤99，0≤x2≤99，10≤x3≤200，10≤x4≤200

表8列出了DPHBA與對比算法求解壓力容器設計問題的實驗結果，其中加粗字數字表示最優值。

根據表8的數據，DPHBA的平均值、標準差、最小值、最大值都為最低，顯示出將SMA和HBA的優點相結合并采用柯西隨機反向擾動策略，使得算法的搜索效率得到極大的改善，從而使其在處理復雜的工程設計問題時能夠發揮出最佳效果。

通過觀察圖5可以發現，DPHBA的收斂速度和準確率都遠遠超過其他算法，這表明在引入HBA的改良策略后，其收斂能力和準確率都大大提升。此外，通過改善初始化種群的方式能夠提升種群的多樣性和遍歷能力，從而使得生成的初始值更接近全局最優。經過SMA和HBA的綜合運用，該算法的收斂速度大大提高，采用交叉操作能夠更加準確地找到局部最優解，從而為工程設計領域的求解帶來更多的可能性。

6 結束語

為了解決原始HBA在處理大規模問題時收斂速度慢、容易陷入局部最優的問題，本文提出雙種群協同演化的改進蜜獾算法。引入了Cubic混沌映射初始化蜜獾種群，使得個體分布更加均勻；同時提出了雙種群協同演化機制充分發揮不同算法的優點，提高了整個算法的搜索效率和優化性能；另外，柯西隨機反向擾動策略的引入也增加了算法的魯棒性。數值實驗表明，本文提出的DPHBA的不同改進策略均取得了顯著有效的效果，并且具有更高的競爭力。求解工程優化設計問題的實驗結果也表明該算法具有較好的應用潛力，能夠提供優秀的解決方案，在工程設計等復雜問題求解中具有廣泛的應用前景。今后將進一步拓寬DPHBA的應用領域，著重于數據挖掘、圖像處理、網絡優化等方面，這將為DPHBA在實際應用中的推廣和進一步研究提供更加廣闊的空間。

參考文獻：

［1］任潔， 彭建文. 求解多目標優化問題的非單調牛頓法的超線性收斂［J］. 應用數學， 2022，35（4）： 956-965. （Ren Jie， Peng Jianwen. Superlinear convergence of nonmonotone Newton method for solving multiobjective optimization problems［J］. Mathematica Applicata， 2022，35（4）： 956-965.）

［2］高偉男， 楊濤， 柴天佑. 基于自適應動態規劃和梯度下降法的自適應最優輸出調節［J］. 控制與決策， 2023，38（8）： 2425-2432. （Gao Weinan， Yang Tao， Chai Tianyou. Adaptive optimal output regulation based on adaptive dynamic programming and gradient descent method［J］. Control and Decision， 2023，38（8）： 2425-2432.）

［3］何慶， 吳意樂， 徐同偉. 改進遺傳模擬退火算法TSP優化中的應用［J］. 控制與決策， 2018，33（2）： 219-225. （He Qing， Wu Yile， Xu Tongwei. Application of improved genetic simulated annealing algorithm in TSP optimization［J］. Control and Decision， 2018，33（2）： 219-225.）

［4］Glover F W. Tabu search， part I［J］. ORSA Journal on Computing， 1989，1（3）： 190-206.

［5］Kennedy J， Eberhart R. Particle swarm optimization［C］//Proc of International Conference on Neural Networks. Piscataway， NJ： IEEE Press， 1995：1942-1948.

［6］Mirjalili S， Mirjalili S M， Lewis A. Grey wolf optimizer［J］. Advances in Engineering Software， 2014，69（3）： 46-61.

［7］Mirjalili S. SCA： a sine cosine algorithm for solving optimization problems［J］. Knowledge-Based Systems， 2016，96（3）： 120-133.

［8］Braik M S. Chameleon swarm algorithm： a bio-inspired optimizer for solving engineering design problems［J］. Expert Systems with Applications， 2021，174（7）： 114685.

［9］Peraza-Vázquez H， Pena-Delgado A F， Echavarría-Castillo G， et al. A bio-inspired method for engineering design optimization inspired by dingoes hunting strategies［J］. Mathematical Problems in Engineering， 2021，2021： article ID 9107547.

［10］邱仲睿， 苗虹， 曾成碧. 多策略融合的改進黏菌算法［J］. 計算機應用， 2023，43（3）： 812-819. （Qiu Zhongrui， Miao Hong， Zeng Chengbi. Improved slime mould algorithm with multi-strategy fusion［J］. Journal of Computer Applications， 2023，43（3）： 812-819.）

［11］董紅偉，李愛蓮，解韶峰. 多策略改進的蜜獾優化算法［J/OL］. 小型微型計算機系統.（2022-11-24）．http：//kns.cnki.net/kcms/detail/21.1106.TP.20221123.1326.032.html. （Dong Hongwei，Li Ailian，Xie Shao-feng， et al. Much honey badgers optimization algorithm of improvement［J/OL］.Journal of Chinese Computer Systems.（2022-11-24）.http：//kns.cnki.net/kcms/detail/21.1106.TP.20221123.1326.032.html.）

［12］劉威， 付杰， 周定寧， 等. 基于改進郊狼優化算法的淺層神經進化方法研究［J］. 計算機學報， 2021，44（6）： 1200-1213. （Liu Wei， Fu Jie， Zhou Dingning， et al. Research on shallow neural network evolution method based on improved coyote optimization algorithm［J］. Chinese Journal of Computers， 2021，44（6）： 1200-1213.）

［13］鐘華庚， 羅高生， 王芳. 一種Halton序列的HDRRT移動機器人融合規劃算法［J］. 控制與決策， 2023，38（6）： 1551-1559. （Zhong Huageng， Luo Gaosheng， Wang Fang. A Halton sequence fusion planning algorithm for HDRRT mobile robots［J］. Control and Decision， 2019，38（6）： 1551-1559.）

［14］張海林， 陳泯融. 基于混合策略的改進哈里斯鷹優化算法［J］. 計算機系統應用， 2023，32（1）： 166-178. （Zhang Hailin， Chen Minrong. Improved Harris hawks optimization algorithm based on hybrid strategy［J］. Computer Systems & Applications， 2019，32（1）： 166-178.）

［15］顧清華， 李學現， 盧才武， 等. 求解高維復雜函數的遺傳灰狼混合算法［J］. 控制與決策， 2020，35（5）： 1191-1198. （Gu Qinghua， Li Xuexian， Lu Caiwu， et al. Hybrid genetic grey wolf algorithm for high dimensional complex function optimization［J］. Control and Decision， 2020，35（5）： 1191-1198.）

［16］董奕含， 喻志超， 胡天躍， 等. 基于改進蜣螂優化算法的瑞雷波頻散曲線反演方法［J］. 油氣地質與采收率， 2023，30（4）： 86-97. （Dong Yihan， Yu Zhichao， Hu Tianyue， et al. Inversion of Rayleigh wave dispersion curve based on improved dung beetle optimizer algorithm［J］. Petroleum Geology and Recovery Efficiency， 2023，30（4）： 86-97.）

［17］Wang Chuang， Wang Zidong， Han Qinglong， et al. Novel leader-follower-based particle swarm optimizer inspired by multiagent systems： algorithm， experiments， and applications［J］. IEEE Trans on Systems， Man， and Cybernetics： Systems， 2022，53（3）： 1322-1334.

［18］徐碧陽， 覃濤， 魏巍， 等. 基于多策略改進的蜜獾優化算法［J/OL］. 小型微型計算機系統.（2023-02-07）. http：//kns.cnki.net/kcms/detail/21.1106.TP.2023.02.07.0901.005.html. （Xu Bi-yang， Qin Tao， Wei Wei， et al. Honey badger optimization algorithm based on multi-strategy improvement［J/OL］. Journal of Chinese Computer Systems.（2023-02-07）. http：//kns.cnki.net/kcms/detail/21.1106.TP.2023.02.07.0901.005.html.）

［19］李雅梅， 孟嗣博， 陳雪蓮. 多策略改進的天鷹優化算法及其應用［J］. 計算機應用研究， 2023，40（5）： 1352-1359. （Li Yamei， Meng Sibo， Chen Xuelian. Multi-strategy improved aquila optimizer and its application［J］. Application Research of Computers， 2023，40（5）： 1352-1359.）

［20］Liang Jianhui， Wang Lifang， Ma Miao. An adaptive dual-population collaborative chicken swarm optimization algorithm for high-dimensional optimization［J］. Biomimetics， 2023，8（2）： 210.

［21］Hashim F A， Houssein E H， Hussain K， et al. Honey badger algorithm： new metaheuristic algorithm for solving optimization problems［J］. Mathematics and Computers in Simulation， 2022，192（2）： 84-110.

［22］Palacios A. Cycling chaos in one-dimensional coupled iterated maps［J］. International Journal of Bifurcation and Chaos， 2002，12（8）： 1859-1868.

［23］Feng Junhong，Zhang Jie，Zhu Xiaoshu，et al. A novel chaos optimization algorithm［J］. Multimedia Tools & Applications， 2017，76： 17405-17436.

［24］錢敏， 黃海松， 范青松. 基于反向策略的混沌麻雀搜索算法［J］. 計算機仿真， 2022，39（8）： 333-339，487. （Qian Min， Huang Haisong， Fan Qingsong. Chaotic sparrow search algorithm based on opposition-based strategy［J］. Computer Simulation， 2022，39（8）： 333-339，487.）

［25］Long Wen， Jiao Jianjun， Liang Ximing， et al.A random opposition-based learning grey wolf optimizer［J］.IEEE Access， 2019，7：113810-113825.

［26］柴巖， 任生. 雙向經驗引導與極端個體調控的HHO算法［J］. 計算機科學與探索， 2023，17（9）： 2118-2136. （Chai Yan， Ren Sheng. HHO algorithm based on bidirectional experience guidance and extreme individual regulation［J］. Journal of Frontiers of Computer Science and Technology， 2023，17（9）： 2118-2136.）

［27］Mirjalili S， Lewis A. The whale optimization algorithm［J］. Advances in Engineering Software， 2016，95（5）： 51-67.

［28］Arora S. Butterfly optimization algorithm： a novel approach for global optimization［J］. Soft Computing， 2019，23（3）： 715-734.