中小型高技術企業創新效率研究

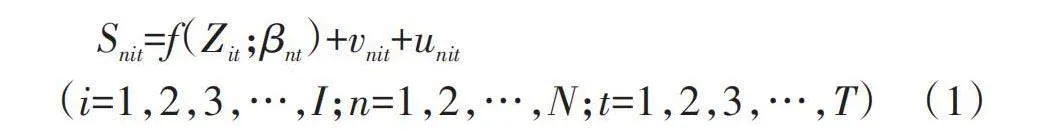
摘要：以68家新三板醫療儀器設備及儀器儀表制造業企業為樣本，采用三階段數據包絡分析（Data Envelopment Analysis，DEA）模型和Malmquist指數分解模型分別從靜態和動態層面對中小型高技術企業的創新效率進行測算。結果發現：在靜態層面，剝離了環境因素和隨機干擾后，新三板的醫療儀器設備及儀器儀表制造企業的整體綜合效率偏低，純技術效率被嚴重低估，規模效率被高估，主要的制約因素由純技術效率轉變為規模效率；在動態層面，全要素生產率（Total Factor Productivity，TFP）增速逐年下滑，后勁不足。因此，政府應與企業一起努力，擴大創新投入規模，深化“產、學、研”合作，保持企業創新效率的上升勢頭，實現中小型高技術企業的高質量發展。

關鍵詞：新三板；企業創新效率；三階段DEA模型；Malmquist指數

中圖分類號：F276.44" " " "文獻標識碼：A" " " 文章編號：1674-0688（2024）02-0034-07

0 引言

我國經濟發展已由高速增長階段轉向高質量發展階段，社會主要矛盾已經轉化為人民日益增長的美好生活需要和不平衡不充分的發展之間的矛盾，發展中的矛盾和問題集中體現在發展質量上，而高質量發展就是解決新時代主要矛盾的“鑰匙”。 習近平總書記在黨的二十大報告中指出，高質量發展是全面建設社會主義現代化國家的首要任務。要想實現高質量發展，就必須實現依靠創新驅動的內涵型增長，高技術企業作為推動我國技術創新與產業結構升級的中堅力量，在構建科技創新體系與促進經濟增長的過程中占有舉足輕重的地位。同時，高技術產業中的中小企業在支撐經濟增長、提升創新能力、擴大社會就業等方面發揮著重要作用。但是，當前我國的中小型高技術企業在發展過程中存在一系列問題，如創新效率有待提高、創業環境有待優化、融資渠道有待拓寬等［1］。

2013年，全國中小企業股份轉讓系統（NEEQ，簡稱新三板）市場正式接受全國中小型企業掛牌申請，為無法順利上市的眾多中小型企業創造了融資機會和途徑，為其提供了更廣闊的發展空間，在一定程度上解決了當前中小型企業融資難的問題。新三板的定位是為創新型、創業型、成長型中小型企業服務，涉及電子信息技術、新材料技術、新醫藥等知識和技術密集型產業，是創新生態系統中非常重要的一個環節，因此對新三板的中小型高技術企業的創新效率進行深入研究，對我國實現依靠創新驅動的經濟內涵型增長具有重要意義。

1 文獻綜述

AFRIAT［2］首先提出了“企業創新效率”的概念，并將它創造性地與“生產前沿”聯系在一起，之后國內外學者對企業創新效率展開了大量研究。例如，LEE 等［3］運用DEA-malmquist模型和聚類分析法考察了合作和合作類型對中小企業創新效率的影響，并提出相應的策略；VIPUT等［4］探究了企業對市場的控制權和企業創新效率之間的關系，實證得出更活躍的收購市場在很大程度上遏制了創新。國內對企業創新效率的研究大致可以歸納為兩類。一是研究企業內部和外部因素對企業創新效率的影響，例如陳習定等［5］認為管理層持股比例對企業技術創新效率具有顯著的正向影響，并表明管理層持股在技術創新實踐中具有激勵相容效應；許冠南等［6］基于社會網絡視角，探討了創新生態系統知識網絡嵌入連通度和支配度對企業技術創新績效的影響機制。二是對各行業的企業創新效率進行測算和評價，例如王乾宇等［7］運用三階段DEA模型，對北京中關村科技園的科技企業進行創新效率評價，認為中關村科技園中技術密集型企業比資源密集型企業的創新效率更高。徐書彬等［8］采用三階段DEA模型對人工智能企業的創新效率進行測算，得出多數人工智能企業的綜合效率和純技術效率處于較低水平。

目前，針對企業創新效率的研究成果眾多，但對新三板企業創新效率的研究成果較少，對其研究多集中于融資效率的分析方面［9-10］。新三板作為服務創新型中小企業的主陣地，其中的企業在很大程度上能代表目前我國中小型高技術企業的發展水平，所以對其開展研究具有重要的意義。但是，考慮到新三板的高技術企業眾多，數據獲取和整理難度大，因此選取高技術產業（制造業）六大類中于2022年投資增長最快的醫療儀器設備及儀器儀表制造業企業為例進行研究。綜上所述，本文采用三階段DEA模型和Malmquist指數分解模型，從靜態和動態兩個層面對新三板醫療儀器設備及儀器儀表制造業企業的創新效率進行測算和評價，并分析影響其創新效率的環境因素。

2 研究方法與數據說明

2.1 面板三階段DEA模型

三階段DEA模型由FRIED等［11］提出，是在傳統DEA模型的基礎上剔除環境因素和隨機干擾因素的影響，可以更加真實地反映決策單元的效率。但是，三階段DEA模型只適用于截面數據的效率測算，若將三階段DEA模型用于面板數據的效率測算，就會出現跨年效率值不在統一前沿面下的問題，從而無法對不同年份的效率值進行直接對比與分析。所以，本文借鑒劉自敏等［12］提出的面板三階段DEA模型，對新三板醫療儀器設備及儀器儀表制造業企業的創新效率進行測算，具體步驟如下。

第一階段：傳統DEA（Data Envelopment Analysis）-BBC（Banker-Charnes-Cooper）模型。本文構建投入導向下基于規模報酬可變的DEA-BCC模型，以原始的投入產出數據為基礎，將跨年的決策單元數據分解為橫截面數據，即將不同年份的同一決策單元看作不同的決策單元，從而測算出各自相應的效率值與投入松弛值。鑒于傳統DEA模型已經被學者廣泛地運用于各類效率測算，因此本文不再贅述其表達式。其中，測算的效率值包括綜合效率（TE）、純技術效率（PTE）和規模效率（SE），綜合效率為純技術效率和規模效率的乘積，即TE=PTE×SE。當TE、PTE、SE值均為1時，表示DEA有效；當PTE、SE僅有一個值為1時，表示DEA弱有效；當TE、PTE、SE都小于1時，表示DEA無效［13］。

第二階段：相似面板隨機前沿（SFA）模型。在第一階段得出的投入松弛值為原始投入值和投入目標值之差，其包含管理效率、環境因素和統計噪聲。然而，傳統的DEA模型未考慮到環境因素和隨機干擾因素對效率值的影響，造成最終測算結果失真。所以，第二階段利用SFA模型對投入松弛值進行分析，其計算公示如下：

Snit=f（Zit；βnt）+vnit+unit

（i=1，2，3，…，I；n=1，2，…，N；t=1，2，3，…，T）" " （1）

其中：Snit是第t年的第i個決策單位的第n項投入松弛值；Zit為環境變量集合；βnt為所選環境變量的待估參數；f（Zit；βnt）表示環境變量對松弛變量Snit的影響；vnit表示隨機干擾項，unit為管理無效率項，vnit+unit為混合誤差項。考慮到unit是否具有時變性，使用SFA模型時，首先估計時變衰退模型的管理無效率項，時變衰退模型的特征為uit= exp {-η（ t-Ti） } ui，η為衰退系數，Ti是DMUi的最后一個時期；其次對估計的衰退系數η進行檢驗，如果拒絕η=0原假設，則說明應使用時變衰退模型（Time-invariant Model），反之則使用非時變模型（Time Varying Decay Model）。

基于公式（1）計算環境變量、隨機干擾項和管理無效率項對投入松弛值的影響后，接下來對投入變量進行調整，使所有的決策單元都處于相同的環境條件和隨機干擾項下，調整公式如下：

[XAnit=Xnit+[max（f（Zit；βnt））-f（Zit；βnt）]+]

[[max（vnit）-vnit]]" " " " " " " " " " " " " " " " " " " " " " " " " " " " " "（2）

（i=1，2，3，…，I；n=1，2，…，N；t=1，2，3，…，T）

其中：[XAnit]和[Xnit]分別表示調整后的投入變量和調整前的投入變量，[[max（f（Zit；βnt））-f（Zit；βnt）]]表示對環境變量進行調整，[[max（vnit）-vnit]]表示對隨機誤差項進行調整。

第三階段：調整后的DEA-BCC模型。將調整后的投入變量替代原始的投入變量，產出變量保持不變，運用DEA-BCC模型對各個決策單元的效率進行測算，最終得到剝離了環境因素和隨機干擾項的實際效率值。

2.2 Malmquist指數分析模型

Malmquist指數又被稱為全要素生產率，是以DEA模型為基礎的動態效率分析方法［14］。Malmquist指數最早由Malmquist提出，此后有研究人員將其與DEA方法相結合，對全要素生產率進行分解，其具體表達式如下：

M（[t+1，yt+1][，xt，yt]）[ Dt（xt+1，yt+1）Dt（xt，yt）×Dt+1（xt+1，yt+1）Dt+1（xt，yt）1/2]（3）

其中：x表示投入變量，y表示產出變量，t表示時期數；Dt和Dt+1分別表示以t時期的技術為參照的t時期和t+1時期的距離方程。若M值大于1，表明從t時期到t+1期效率提升；若M值小于1，則表明從t時期到t+1時期效率下降；若M值等于1，則表明效率不變。

Malmquist指數分析模型將全要素生產率（TFP）進一步分解為綜合技術效率變化（EFFCH）、技術進步變化（TECHCH）、純技術效率變化（PECH）和生產規模變化（SECH），其關系公式如下：

TFP=EFFCH×TECHCH" " " " " " " " " " " （4）

EFFCH=PECH×SECH" " " " " " " " " " " "（5）

TFP=TECHCH×PECH×SECH" " " " " " " " "（6）

2.3 樣本選取

本文主要研究新三板高技術企業的創新效率，由于新三板的高技術企業數量眾多，因此根據國家統計局印發的《高技術產業（制造業）分類（2017）》，選取醫療儀器設備及儀器儀表制造業企業作為研究對象。由于企業技術創新具有一定的滯后性，本文采取已有研究的做法［15］，將產出做1年的滯后處理，即需要收集2016—2020年的投入數據和相關環境數據及2017—2021的產出數據。對原始數據進行清洗剔除：①ST（Special Treatment）、PT（Particular Transfer）類企業；②年報信息嚴重缺失的企業；③年度專利申請數為0的企業；④2016—2021年退出新三板的企業。最終，選取剩余的68家醫療儀器設備及儀器儀表制造業企業作為樣本企業。

2.4 變量選取

2.4.1 投入和產出變量

根據以往學者的研究［16］，投入指標一般從勞動力及資本兩個角度考慮。借鑒以往學者的研究經驗及數據的可得性，本文選取研發技術人員數量和研發費用作為投入指標。創新產出有很多種類，根據屬性不同，可以將其分為知識產出和經濟產出。知識產出水平一般采用專利數量衡量，而專利數量又分為專利申請數量和專利授權數量，但由于專利授權周期較長，受其他因素影響較大，所以選取專利申請數量對創新知識產出水平進行衡量。醫療儀器設備及儀器儀表制造業企業定位為高技術企業，其主要業務與高技術類產品相關，所以選取企業的主營業務收入對經濟產出水平進行衡量。因此，本文選取的產出指標為專利申請數量和主營業務收入。DEA模型要求投入和產出指標符合“同向性”假定，即投入量增加時，產出量也增加。所以，為了保證選取指標的科學性，需采取Pearson相關系數法對其進行檢驗。利用Stata16.0軟件計算，得到專利申請數量與研發技術人員數量和研發費用的相關系數分別為0.255和0.335，主營業務收入與研發技術人員數量和研發費用的相關系數分別為0.474和0.545。各投入指標與產出指標之間的相關系數均在1%水平上顯著為正，符合“同向性”假定，指標選取合理。

2.4.2 環境變量

根據SIMAR等［17］提出的“分離假設”，環境變量為能夠對企業創新效率產生顯著影響但企業難以主觀控制或者短時間改變的因素。根據以往學者的研究［7-8，16］，環境變量通常包括外部經濟因素、企業內部因素、政府政策因素等。結合新三板的高技術企業發展的實際情況，本文選取如下環境變量。

（1）外部經濟因素：區域經濟結構的不同導致經濟發展不平衡的問題一直存在，企業所處的區位不同，其經濟發展水平差異也較大。地區經濟發展水平較高的地區往往能夠吸引更多的人才和資金，協同創新的引領作用更強，企業也能享受更好的信息和基礎服務，更有利于企業開展創新。因此，本文選取地區發展水平和對外開放水平兩個變量分析外部經濟因素。

（2）企業內部因素：隨著企業的發展，企業的領導、戰略、規模和融資能力等因素都會對企業創新效率產生影響。因此，本文選取企業規模、股權集中度、資產負債率和企業所處市場層級分析企業內部因素。

（3）政府政策因素：中小型高技術企業開展創新面臨的一大難題就是融資能力弱，但企業研發需要長期、大量且穩定的資金支持，離不開政府的財政補貼和支持。因此，本文選取政府補助金額分析政府政策因素。

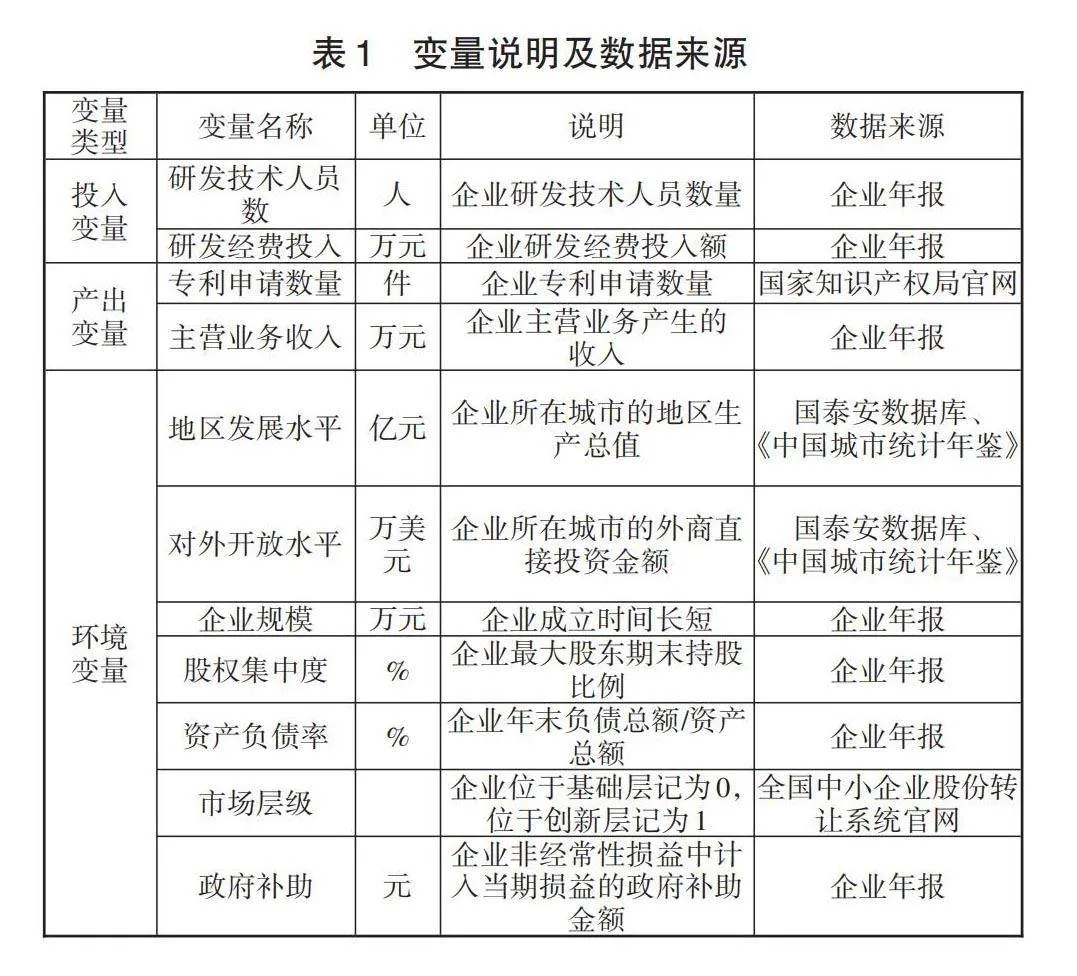
各變量的具體說明及數據來源見表1。為了使環境變量具有可比性，本文將其進行標準化處理，使第二階段的結果更加準確。

3 實證結果分析

3.1 三階段DEA的實證結果分析

3.1.1 第一階段的傳統DEA-BCC模型測量結果

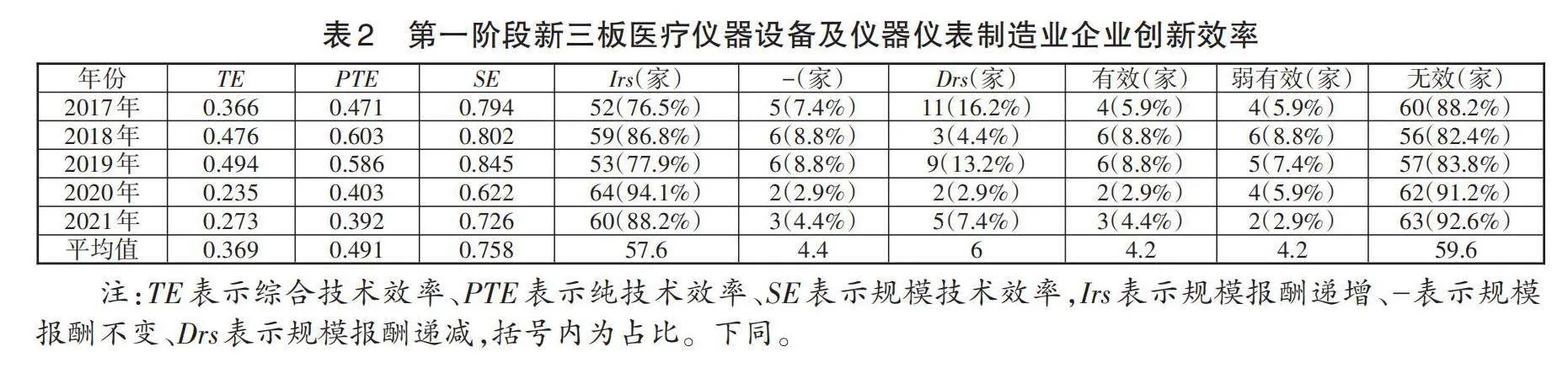
根據68家新三板醫療儀器設備及儀器儀表制造業企業5年的原始投入和產出數據，利用DEAP2.1軟件對第一階段的創新效率進行測算（見表2）。從總體上來看，綜合技術效率、純技術效率、規模效率的平均值分別為0.369、0.491、0.758，說明樣本企業的創新效率不高，有較大的上升空間，并且主要受純技術效率的制約，即企業的資源配置和管理水平都有待提高。規模報酬遞增的企業數量明顯多于規模報酬遞減的企業數量，達到DEA有效的企業數量為2～6家，達到DEA有效的企業數量占總樣本企業數量的比例不到7%，多數企業DEA無效，平均占比達到87.6%。從變化趨勢來看，在觀察期內，樣本企業2017—2019年的綜合技術效率平均值呈上升趨勢，2020年的下降趨勢較明顯，2021年有略微上升，可能是受新型冠狀病毒感染疫情的影響。規模報酬遞增和DEA有效的企業數量呈輕微波動變化，沒有明顯增加或減少。但是，由于本階段的測算結果沒有考慮到環境噪聲和隨機干擾項的影響，存在各企業創新效率測算失真的可能性，因此需要對投入變量進行調整。

3.1.2 第二階段的SFA模型的回歸結果

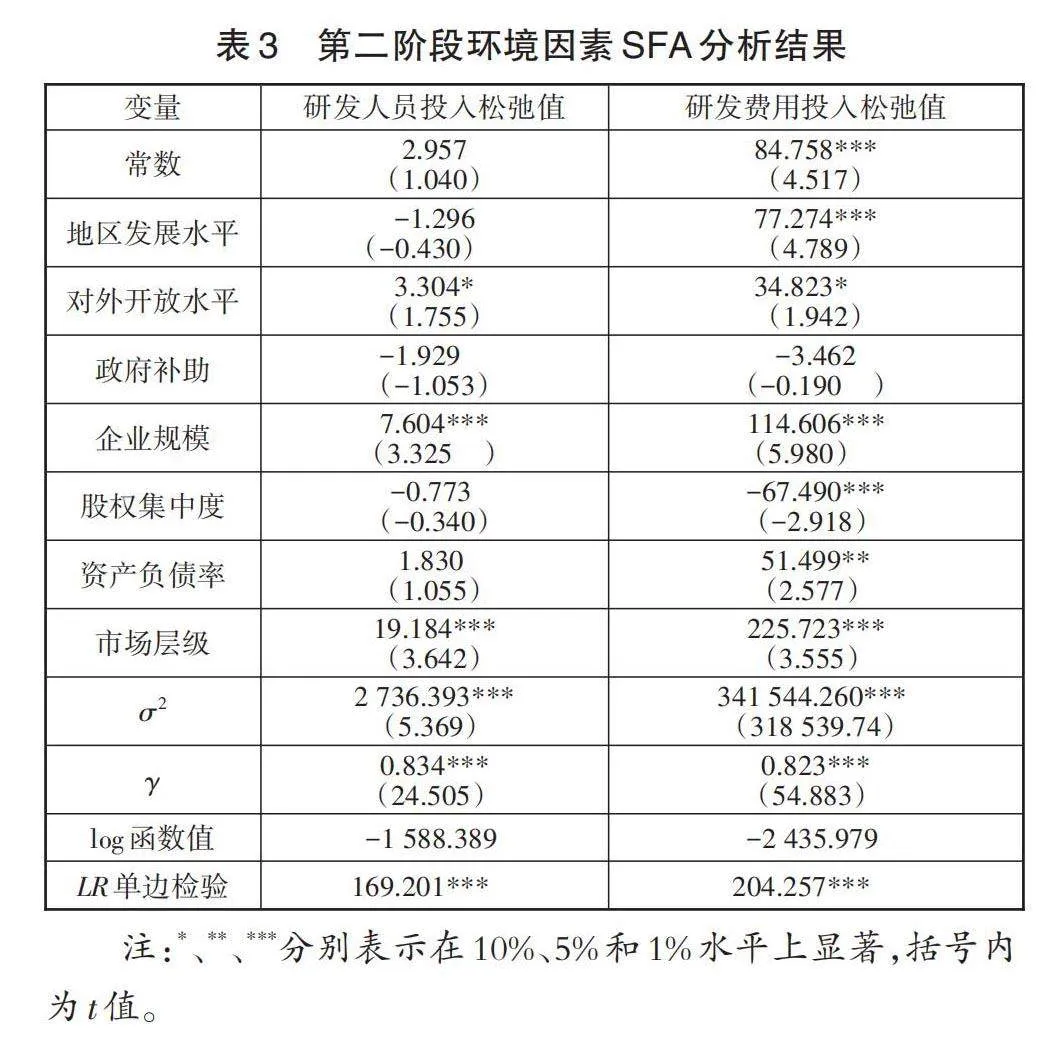
本階段運用Frontier4.1軟件，將第一階段測量結果中得到的研發人員及研發費用投入的投入松弛值作為被解釋變量，7個環境變量作為解釋變量，得到環境因素SFA模型分析結果（見表3）。研發人員投入和研發費用投入的單邊誤差似然比檢驗LR值均在1%水平下顯著。拒絕了不存在管理無效率項的原假設，表明模型設置合理，可以運用SFA模型進行回歸分析。γ值分別為0.834和0.823，表明在混合誤差項中管理無效率的影響占主導地位。研發人員投入和研發費用投入的單邊誤差似然比檢驗LR值均在1%水平下顯著。拒絕了不存在管理無效率項的原假設，表明模型設置合理，可以運用SFA模型進行回歸分析。若回歸系數為負，則表示該環境變量的增加會導致松弛變量降低，對投入冗余的降低起正向作用，有利于提高企業的創新效率。據此，本文對表3中對投入松弛變量具有顯著影響的環境變量做出如下分析。

（1）地區發展水平。該變量與研發人員投入松弛值呈負相關但不顯著，與研發費用投入松弛值存在正向影響且在1%水平下顯著。說明隨著地方發展水平的提高，研發費用投入冗余也會相應增加，造成了資金浪費，從而導致企業創新效率降低。較高的發展水平能為高技術企業提供更好的市場環境和融資環境，但是也意味著企業將會要面臨更大的競爭壓力，從而導致企業盲目增加研發費用。從樣本企業中也可以發現，人均GDP較高地區的企業的綜合效率普遍低于人均GDP較低地區的企業，但產出指標卻相反，表明了處于經濟發達地區的企業仍沒有逃脫高技術產業“高產出，低效益”的陷阱［18］。

（2）對外開放水平。該變量與研發人員和研發費用的投入松弛值均存在正向影響且在10%水平下顯著。對外開放水平高可以破除區域間的壁壘，意味著該地區進入壁壘低，進入的企業多，從而導致市場競爭更加激烈，導致企業盲目增加研發資金，研發人才的引進和研發資金的投入導致投入冗余，降低了企業創新效率。

（3）企業規模。該變量與研發人員和研發費用的投入松弛值均存在正向影響且在1%水平下顯著。企業規模擴大意味著企業有更多的資金及更強烈的意愿進行研發，那么對于研發人員和研發費用的投入就會增大，從而容易造成投入冗余。

（4）股權集中度。該變量與研發人員投入松弛值呈負相關但不顯著，與研發費用投入松弛值存在反向影響且在1%水平下顯著。說明股權集中度越高，越有利于減少投入冗余，提高企業創新效率，這與已有的研究結論一致。郭玉晶等［19］認為，在一定的界限下，大股東持股比例越高，企業創新效率也會越高，起到了一定的促進作用。從傳統的委托代理理論視角進行分析，大股東持股能夠減輕股東與經理之間的代理沖突，更有利于大股東對管理層的控制，降低代理成本，有利于企業綜合創新效率的提升。

（5）資產負債率。該變量與研發人員投入松弛值呈正相關但不顯著，與研發費用投入松弛值存在正向影響且在5%水平下顯著。盡管資產負債率的上升意味著企業負債增多，償債能力下降，但說明了企業是通過舉借外債籌集資金，企業有更多的資金用于發展和研發，導致研發費用投入冗余增加，不利于企業創新效率的提升。

（6）市場層級。該變量與研發人員和研發費用的投入松弛值均存在正向影響且在1%水平下顯著，說明企業位于創新層會顯著加重研發人員和研發費用的投入冗余情況。企業進入創新層后，能夠獲得資本市場各參與方更多的關注，自身的融資能力得到增強，從而可以投入更多的人力、物力進行研發，導致冗余現象的可能性增大。

各環境變量對于不同投入的影響方向和作用強度不同，從而造成測算結果存在一定的偏差，導致得到的結果缺乏真實性和科學性。因此，必須對原始投入變量進行調整，使得各決策單元處于同樣的環境條件和隨機干擾項下，保證效率測算的準確性。

3.1.3 第三階段調整后的DEA模型測量結果

第二階段應用 SFA對原始投入變量進行環境因素和隨機因素剝離分析后，利用DEAP2.1軟件對原始產出變量和修正后的投入變量重新進行創新效率的測算（見表4）。對比第一階段和第三階段的數據，做出如下分析。

（1）總體創新效率分析。投入調整后，綜合效率平均值從0.369下降至0.332，降幅為10.0%左右，按年份來看，2017—2019年的綜合效率有所下降，但2020—2021年受剝離環境因素和隨機因素的影響，綜合效率有所上升，再一次證實了新型冠狀病毒感染疫情導致的外部環境變差，進而對綜合效率造成影響。純技術效率平均值從0.491上升至0.913，增幅為85.9%左右，表明受外部環境影響，純技術效率被嚴重低估。規模效率由0.758下降至0.368，降幅為51.5%左右，同理可得，受外部環境的影響，規模效率被高估。綜上可以看出，新三板醫療儀器設備及儀器儀表制造業企業的整體創新效率不高，其主要制約因素由純技術效率轉變為規模效率，這與實際情況相符。新三板主要面向中小微型企業，企業規模普遍較小，再加上中小型高技術企業普遍面臨融資難等問題，難以形成規模優勢。

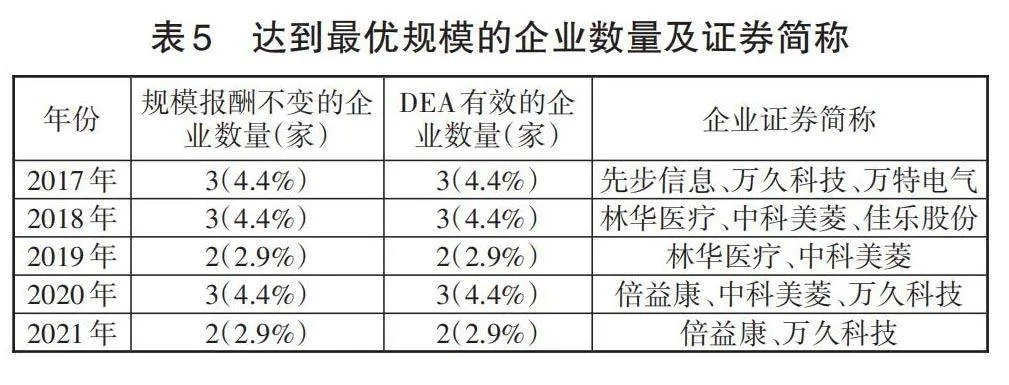
（2）規模報酬分析。投入調整后，規模報酬遞增企業數量的平均值由57.6上至64.8，增幅為12.5%左右，規模報酬遞增的企業數量占總樣本企業數量的比例高達95.3%。說明絕大部分的企業未達到最優規模，限制了其總體創新效率的提升，與上文總體創新效率的分析結論相符。規模報酬不變企業數量的平均值由4.4下降至2.6，降幅為40.9%左右，數量在2～3家的范圍內浮動，達到最優規模企業的數量及證券簡稱見表5。

（3）DEA有效性分析。投入調整后，達到DEA有效和規模報酬不變的企業數量下降。達到弱有效的企業數量上升，平均值由4.2上升至9，增幅為114.3%左右。并且，第一階段和第三階段的弱有效企業均為純技術效率有效，規模效率無效，再次說明了受環境因素的影響，純技術效率被低估，也說明了提升規模效率可以讓弱有效的企業達到DEA有效，但仍有82.9%（平均值）的企業處于DEA無效的狀態，表明大部分企業沒有處于生產前沿面，仍有提升的空間。

3.2 基于面板數據Malmquist指數的動態分析結果

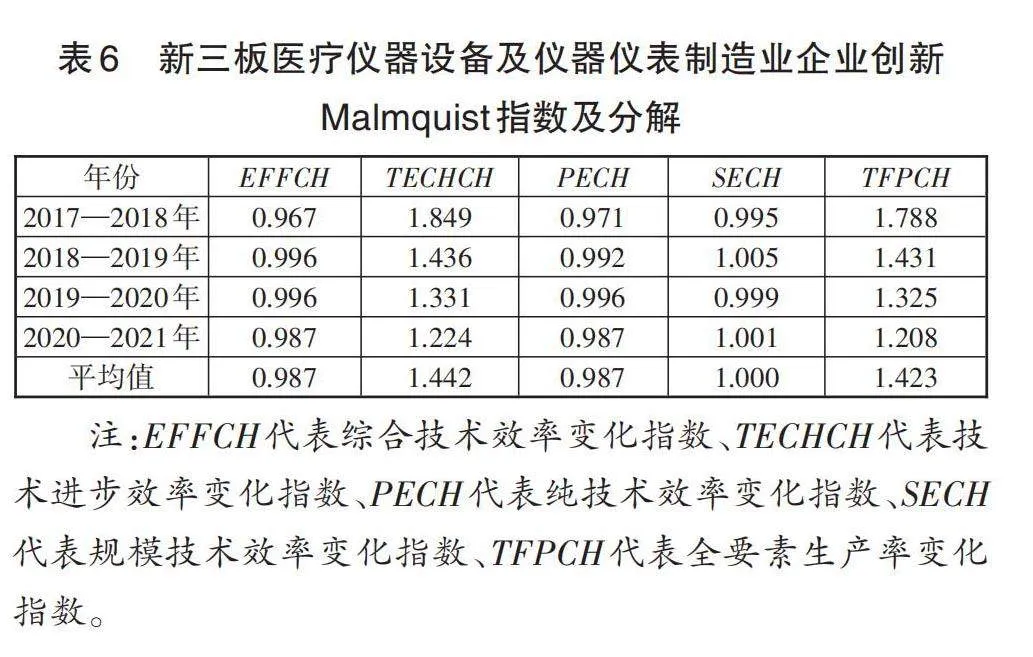
由于三階段DEA模型測算的效率值僅能反映某一年份決策單元的靜態效率情況，不能進行動態的效率變動時間序列比較分析，所以運用DEAP2.1軟件，將剝離了環境影響因素和隨機干擾項后的投入變量和原始產出變量帶入Malmquist指數模型進行測算，結果見表6。表6中的數據反映了新三板醫療儀器設備及儀器儀表制造業企業的整體變動情況。

從整體來看，全要素生產率變化每年都處于增長的狀態，變化指數均大于1，但增長的比率逐年下降，說明樣本企業的創新效率逐步上升，但是后勁不足。綜合技術效率變化整體較平穩，變化指數均小于1，呈平均值-1.3%的負增長趨勢，純技術效率與綜合技術效率一致，表明了企業管理水平從整體上降低了企業的創新效率。規模效率變化指數均接近1，整體變化也較平穩，再次暴露了新三板高技術企業規模小、研發實力弱的缺陷。創新效率的增長基本是由技術進步帶來的，技術進步平均增長率為44.2%，增長率和全要素生產率逐年下降。總的來說，技術進步對于創新效率的貢獻更顯著，技術效率和規模效率都在一定程度上降低了企業的創新效率。

表6 新三板醫療儀器設備及儀器儀表制造業企業創新Malmquist指數及分解

[年份 EFFCH TECHCH PECH SECH TFPCH 2017—2018年 0.967 1.849 0.971 0.995 1.788 2018—2019年 0.996 1.436 0.992 1.005 1.431 2019—2020年 0.996 1.331 0.996 0.999 1.325 2020—2021年 0.987 1.224 0.987 1.001 1.208 平均值 0.987 1.442 0.987 1.000 1.423 ]

注：[EFFCH]代表綜合技術效率變化指數、[TECHCH]代表技術進步效率變化指數、[PECH]代表純技術效率變化指數、[SECH]代表規模技術效率變化指數、[TFPCH]代表全要素生產率變化指數。

4 研究結論與建議

本文運用面板三階段DEA模型以及Malmquist指數分解模型分別從靜態和動態層面對我國68家新三板的醫療儀器設備及儀器儀表制造業企業進行創新效率分析。在剝離了環境因素和隨機干擾后，創新效率發生明顯變化，結論如下：①樣本企業整體的綜合創新效率不高，純技術效率被嚴重低估，規模技術效率被高估，主要的制約因素由純技術效率轉變為規模技術效率。②對外開放水平、企業規模、市場層級會增大研發技術人員投入冗余，地區發展水平、對外開放水平、企業規模、資產負債率、市場層級會增大研發費用投入冗余，限制企業創新效率的提升；而股權集中度會減少研發費用投入冗余，有利于企業創新效率的提升。③68家樣本企業絕大部分沒有達到最優規模，表明大部分企業沒有處于生產前沿面，仍有提升的空間。④在動態層面，全要素生產率的增長率逐年下降，說明樣本企業的創新效率雖然上升，但是后勁不足；技術進步對創新效率的提升有較大的促進作用。

綜上，本文從企業和政府兩個方面提出如下建議：①在企業層面，應在適度擴大創新投入規模的同時，減少資源浪費。只有合理配置創新投入資源，才能優化創新效率，實現企業高質量發展。②在政府層面，近年政府對新三板企業的扶持力度逐年增大，但實證發現，直接的政府補助未對樣本企業的研發技術人員和研發費用投入冗余產生顯著影響，未來可以考慮通過加大對企業的間接補貼力度對新三板的高技術企業予以扶持，例如加大稅收優惠、金融支持力度等。此外，政府應積極優化創新環境，鼓勵新三板的高技術企業進行“產、學、研”合作，提高創新實力，構建長遠的創新戰略，保持企業創新效率的上升勢頭。

5 參考文獻

［1］劉成坤，張秀武.中小型高技術企業Ramp;D效率的評價與分析——基于三階段DEA模型［J］.科技與經濟，2017，30（6）：41-45，50.

［2］AFRIAT N S.Efficiency Estimation of Production Functions［J］. International Economic Review，1972，13（3）：568-598.

［3］LEE J，KIM C，CHOI G.Exploring data envelopment analysis for measuring collaborated innovation efficiency of small and medium-sized enterprises in Korea［J］. European Journal of Operational Research，2019，278（2）：533-545.

［4］VIPUT O，Pattanaporn C，Pornsit J.Does the market for corporate control impede or promote corporate innovation efficiency？ Evidence from research quotient［J］. Finance Research Letters，2022，46（PA）：102212.

［5］陳習定，戴曉震，張芳芳.管理層持股對企業技術創新效率的影響研究［J］.科研管理，2018，39（5）：11-18.

［6］許冠南，胡偉婕，周源，等.創新生態系統雙重網絡嵌入對企業創新的影響機制［J］.管理科學，2022，35（3）：73-86.

［7］王乾宇，薛彪，崔靜靜.基于三階段DEA的中關村科技企業創新效率研究［J］.內蒙古大學學報（自然科學版），2022，53（6）：652-659.

［8］徐書彬，黎新伍，李果.基于三階段DEA的人工智能上市企業創新效率評價［J］.科技管理研究，2020，40（5）：165-172.

［9］沈忱.中小企業在新三板市場融資效率研究——基于三階段DEA模型定向增發研究［J］.審計與經濟研究，2017，32（3）：78-86.

［10］馬莉莉，李湘晉.分層制度、做市商制度與企業融資效率——基于我國新三板掛牌企業的實證研究［J］.經濟問題，2019（3）：56-64.

［11］FRIED O H，LOVELL K A C，SCHMIDT S S， et al. Accounting for environmental effects and statistical noise in data envelopment analysis［J］. Journal of Productivity Analysis，2002，17（1/2）：157-174.

［12］劉自敏，張昕竹，楊丹.我國省級政府衛生投入效率的時空演變——基于面板三階段DEA模型的分析［J］.中央財經大學學報，2014（6）：97-104.

［13］胡麗娜.基于DEA的區域科技創新效率測算與評價［J］.數學的實踐與認識，2019，49（17）：95-101.

［14］陳杰，許朗.基于面板三階段DEA-Malmquist模型的中國農業綠色水資源利用效率研究［J］.地理科學，2023，43（4）：709-718.

［15］王慶金，王強，周雪.區域高技術產業研發活動效率評價及影響因素研究［J］.科技進步與對策，2018，35（23）：59-65.

［16］馮琳潔.基于三階段DEA的創業板企業創新效率評價研究［J］.中國注冊會計師，2022（3）：49-54.

［17］Simar L，Wilson W P.Estimation and inference in two-stage，semi-parametric models of production processes［J］.Journal of Econometrics，2005，136（1）：31-64.

［18］陳凱華，官建成，寇明婷.中國高技術產業“高產出、低效益”的癥結與對策研究——基于技術創新效率角度的探索［J］.管理評論，2012，24（4）：53-66.

［19］郭玉晶，朱雅玲，張映芹.股權結構與上市公司技術創新效率研究——基于三階段DEA與Tobit模型［J］.技術經濟，2020，39（7）：128-139.