基于相關性分析的不完整數據函數依賴挖掘方法

尹詩寧 張安珍 夏秀峰

摘 要：函數依賴（FD）挖掘方法通常專注于發現所有滿足函數依賴語法特征的結果，在數據不完整的情況下常導致大量成立但無意義的FD。針對挖掘無效FD的問題，提出基于相關性分析的不完整數據FD挖掘方法。利用概率圖模型構建具有缺失值屬性的概率分布，通過相關性分析捕捉屬性之間的關聯關系，避免枚舉所有可能性，以挖掘具有統計學意義的FD。實驗結果表明，該方法可以更準確地定位到有意義的FD，與最先進的FD發現方法相比，F1分數平均提高1.5倍。

關鍵詞：函數依賴；相關性分析；不完整數據

中圖分類號：TP301?? 文獻標志碼：A??? 文章編號：1001-3695（2024）05-013-1368-06

doi： 10.19734/j.issn.1001-3695.2023.09.0451

Correlation analysis for discovering functional dependencies in incomplete data

Abstract：Function dependency （FD） discovery methods typically focus on identifying all results that satisfy the syntax features of function dependencies. In the case of incomplete data， it often results in a significant number of established but meaningless FD. In response to the issue of discovering invalid FD， this paper proposed a method for incomplete data FD discovery based on correlation analysis. It constructed a probability distribution with attributes containing missing values using a probability graph model， captured the relationships between attributes through correlation analysis， avoided enumerating all possibili-ties， to discover FD with statistical significance. The experimental results show that the proposed method can more accurately pinpoint meaningful FD， more accurately， with an average F1-score improvement of 1.5 times compared to state-of-the-art FD discovery methods.

Key words：functional dependency; correlation analysis; incomplete data

0 引言

函數依賴（functional dependency，FD）是數據庫管理系統中的一個關鍵概念，用于描述數據庫表中字段之間的關系，在許多領域有著廣泛應用，如數據庫設計、數據清洗、特征選擇等。近年來，研究人員圍繞FD挖掘展開了大量研究工作，這些研究工作通常假設數據是完整的。然而，真實應用中的數據通常存在大量的缺失值，如何在不完整數據中挖掘出正確的FD是一個亟待解決的問題。

不難發現，不完整數據上的FD挖掘比完整數據上的FD挖掘更具挑戰性。一方面，若直接使用現有的完整數據上的FD挖掘方法在不完整數據上進行挖掘，將導致結果中出現大量過擬合的FD規則。這是由于現有的FD挖掘方法通常根據FD的語法特征進行挖掘，導致所有滿足左部取值相同時右部取值也相同的規則出現在結果集中。例如，在只有幾十個屬性的數據集上，會找出成百上千條FD［1］，這些FD中大部分沒有任何統計學意義。另一方面，現有的不完整數據上，FD挖掘方法［2］通常將所有滿足近似度閾值的FD規則挖掘出來，然后再根據缺失值的概率分布驗證每個FD規則的真偽。然而，為了保證在不完整數據上所有真實FD規則都被挖掘出來，需要設置一個很大的近似度閾值，最壞情況下，閾值等于缺失的元組數量，此時，結果中將出現大量假的FD規則。

為此，本文提出基于相關性分析的不完整數據FD挖掘方法，利用FD的語義特征指導挖掘過程，在處理缺失值的同時，挖掘出具有統計學意義的函數依賴。具體過程如下：首先，采用概率圖模型建立各個屬性的概率分布，給出缺失值填充方案正確性概率的計算模型。其次，利用相關性分析捕捉每對屬性之間的關聯關系，保留具有強關聯性的屬性，并組合中度關聯的屬性形成新的候選FD集合。最后，對候選FD進行細化，通過檢查互補的、未經驗證的依賴候選項，直到找到所有最小FD。

綜上所述，本文的主要貢獻如下：

a）提出了一種基于相關性分析的近似函數依賴挖掘方法，利用統計學概念快速定位具有相關性的屬性，使得發現的FD結果可解釋性更好。

b）建立了一種針對缺失值的概率模型，計算缺失值的取值概率，從而避免了缺失值解釋的單一性可能引發的誤差。

c）通過對候選FD細化，檢查互補的、未經驗證的依賴候選項，直到找到所有最小FD，確保輸出的結果是最小且有意義的。

1 相關工作

常見的完整性約束包括函數依賴規則［3～5］、包含依賴規則［6］、順序依賴關系［7］等，其中最常用的是函數依賴規則，得到了學術界的廣泛研究。它有許多應用，如維護數據質量［8］、模式標準化［9］、修復數據不一致［10，11］等。

以TANE［12］為代表的行高效算法，使用分層搜索策略將FD的搜索空間建模為屬性格。晶格從較小的屬性集到較大的屬性集逐級遍歷，并使用剪枝技術縮減搜索空間，以發現精確和近似的FD。后續算法Fun［13］、FD-mine［14］、DFD［15］引入了不同的剪枝和格遍歷策略。該類方法對數據量有良好的擴展性。

列高效算法FDep［16］、DepMiner［17］和FastFDs［18］，通過計算元組的不一致集確定FD的屬性組合，以便生成兩組不同的屬性子集，從這些屬性子集派生候選FD。這類方法對屬性數量有良好擴展，但復雜度是數據量的平方。

混合算法［19，20］在行高效算法和列高效算法之間切換，結合前兩種算法的優點，具體地說，采樣后利用列高效算法得到非函數依賴，使用行高效部分進行驗證，在元組和屬性數量都增加的情況下有更好的伸縮性，但它不適用于近似函數依賴關系。

CORDS考慮相關性以獲得軟FD［21］，只研究LHS上具有單一屬性的FD，提出了一種基于示例的方法，該方法使用系統編目檢索列中不同值的數量。然而，CORDS中考慮的共現度量發現了邊際依賴，而不是對應于真正FD的條件獨立。

上述方法都是基于共現頻率的，當左部屬性多時容易出現過擬合的情況。為此提出了結構學習方法FDX［22］，依賴于稀疏回歸，對樣本進行結構學習，通過從原始數據獲取采樣的元組對的值差異。假設屬性之間有一個全局優先級，通過逆協方差矩陣得到FD。

當數據中有缺失值時，現有FD挖掘方法通常采用以下三種策略。第一種策略是忽略不完整的元組［23］，直接在完整元組集合上挖掘FD規則。然而，這種方法存在一個嚴重問題，結果中可能包含大量虛假的FD規則。這些虛假規則在完整元組集合上成立，但在對應的不完整元組集合上不成立。第二種策略是根據給定的缺失值語義來挖掘FD規則［24］。常見的缺失值語義有兩種：缺失值取值都相同（NULL-EQ）和缺失值取值都不同（NULL-NOT-EQ）。然而，真實的缺失值取值通常更加復雜，可能部分相同、部分不同，這導致在采用NULL-EQ語義時可能會挖掘出大量虛假的FD規則，而采用NULL-NOT-EQ語義時可能會錯過真正的FD規則。第三種策略是首先填充缺失值，然后在填充后的完整數據上進行FD挖掘。然而，這種方法的準確性嚴重依賴于缺失值填充方法的準確性，不準確的填充可能導致錯誤的FD規則。

為了應對這些問題，Berti-quille等人［2］提出了一種方法，利用現有的近似FD挖掘方法在不完整數據上找出所有可能的近似FD規則，然后計算每個規則的概率，只保留概率較高的FD規則。然而，這種方法需要挖掘出所有近似度的FD規則才能保證真實FD規則不會被遺漏，而且后續的概率驗證階段代價非常大。之前關于FD發現的工作并沒有試圖分析缺失值數據上有意義的函數依賴，找出大量近似成立但無效的FD。

現有的解決方案沒有充分利用屬性之間的關聯關系，而是系統地枚舉有可能的FD規則并逐一驗證，導致候選FD挖掘結果效率低且沒有找到有意義的依賴關系。本文引入了相關性分析的方法提高函數依賴挖掘的準確性，大大減少候選FD的規模，有效避免了屬性數量過多導致的過擬合現象。通過對缺失值建立概率模型，規避了僅考慮缺失值解釋的單一性可能帶來的誤差問題。

2 預備知識及問題定義

定義1 函數依賴（functional dependency，FD）。給定屬性集D上的關系模式R。R上的一個FD表示為X→Y，其中XR，Y∈R，表示X中的所有元組唯一地決定Y中的值。更正式地說，設ti［Y］是屬性Y中的元組ti的值；t，t′∈r，t［X］=t′［X］t［Y］=t′［Y］，稱X為FD的左部（LHS），Y為FD的右部（RHS）。

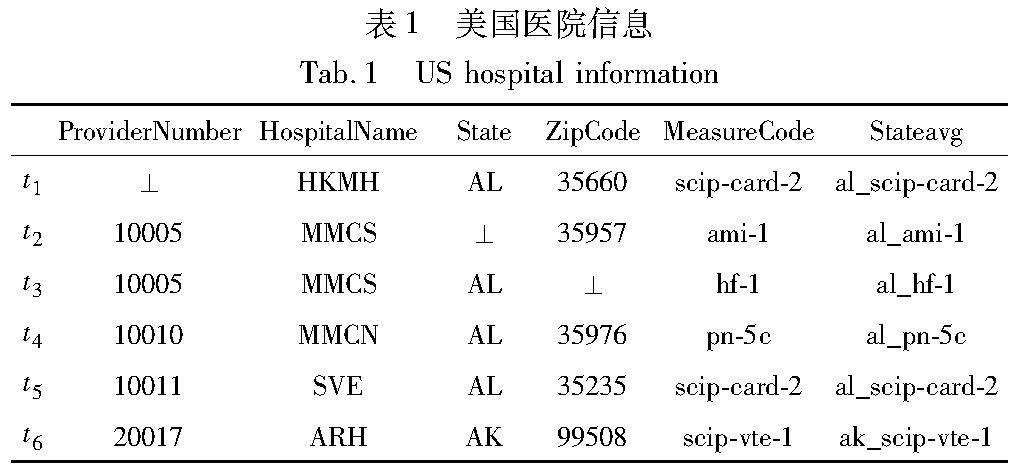
例1 以表1為例，表1為部分美國醫院信息，主要包括醫院編號、名稱所在地、代碼等，假設有FD：ProviderNumber→HospitalName，表示數據集中所有ProviderNumber取值相同的元組，對應屬性HospitalName的取值一定相同。如果不相等，則該數據違反函數依賴規則。

定義2 空語義。將數據集中的缺失值表示為NULL值，用⊥表示。如前所述，在處理NULL值時，傳統上提出了兩種語義：第一種解釋，NULL-EQ，表示為（⊥=⊥），認為所有缺失值都是相同的；第二種語義，NULL-NOT-EQ，表示（⊥≠⊥），認為每個缺失值都是不同的。這兩種語義有不同的動機，并導致發現不同的FD集合。

定義3 卡方檢驗。卡方檢驗是一種用于檢驗兩個分類變量之間是否存在顯著關聯性的統計方法，基于觀察值與期望值之間的差異來判斷兩個變量是否獨立。卡方檢驗的原假設是兩個變量是獨立的，備擇假設是兩個變量之間存在關聯。

定義4 Cramers V系數。Cramers V是用于衡量兩個分類變量之間關聯性強度的指標。它是從卡方統計量中派生出來的，用于標準化卡方統計量，以便在不同的表格尺寸和自由度下進行比較。Cramers V的取值在0～1，值越接近1，表示兩個變量之間的關聯性越強。Cramers V的計算公式為

其中：χ2是卡方統計量；n是樣本總數；k是第一個分類變量的類別數；r是第二個分類變量的類別數。卡方檢驗用于檢驗分類變量之間的關聯性是否顯著，而Cramers V則是一種衡量分類變量關聯性強度的標準化指標。

3 不完整數據上近似函數依賴挖掘方法

針對不完整數據的函數依賴挖掘問題，本文提出基于相關性分析的近似函數依賴挖掘框架，旨在提高不完整近似函數依賴挖掘的效率和可解釋性，緩解過擬合問題。

3.1 不完整數據上近似函數依賴挖掘框架

本文提出的不完整數據上近似函數依賴挖掘方法包括建立概率模型、相關性分析和候選FD規則驗證與細化三個步驟，如圖1所示。輸入為帶有缺失值的數據集D和錯誤閾值，輸出為最小且非平凡的函數依賴集合。

a）建立概率模型：首先，在給定的不完整數據集上訓練貝葉斯網，學習屬性之間的相關關系以及條件概率分布；其次，建模缺失值填充方案正確性概率為P（A|E），即給定完整部分屬性取值時，有缺失值屬性取值的概率；最后，利用貝葉斯推理預測不完整數據的所有取值概率。

b）相關性分析：利用上一步輸出對屬性之間進行相關性分析，對相互獨立的屬性進行剪枝，減小候選FD的規模，剩下的屬性進行逐層搜索，從底層單個節點開始，快速定位候選的FD。

c）候選FD規則驗證與細化：如果LHS和RHS之間有強相關性，則認為這樣的節點是最小的決定集。對于其他的節點進行組合，進一步驗證相關性。如果不滿足閾值，就繼續添加屬性細化，直到滿足閾值或者無法繼續添加屬性，得到完整的FD集合。

3.2 統計學習與推理

本節給出了缺失值概率模型和概率推理方法，目的是根據缺失值取值的概率分布分析屬性之間的相關性。

為了推斷缺失值的概率，使用了一個廣泛使用的概率圖模型——貝葉斯網絡，它提供了一種簡潔地描述屬性的概率分布方法。根據貝葉斯網絡中的局部馬爾可夫性質，每個變量在其父變量的條件下都與非子變量無關。因此，影響一個變量取值分布的變量都在馬爾可夫毯中，通過觀察有缺失值的屬性A的馬爾可夫毯上的屬性，可以推斷出屬性A的可能取值范圍，其他屬性對屬性A的取值不會產生直接影響。將有缺失值的屬性A作為查詢屬性，其他屬性E=attr（R）＼A為證據屬性集，通過證據屬性集預測查詢屬性各個取值的概率。

對于有缺失值屬性A的元組t，有t［E］=t［E1，E2，…，EL］和t［A］。設SE=DOM（E1）×DOM（E2）×…×DOM（EL）表示t的證據屬性的空間，SA=DOM（A）表示t的查詢屬性的空間。假設根據SA×SE上的概率分布P（A，E）隨機生成元組。將t的缺失值概率建模為給定證據屬性值的查詢屬性值的條件概率，即P（A=t［A］|E=t［E］）（簡稱P（t［A］|t［E］）），根據貝葉斯定理可得

給定總體上的貝葉斯網絡，網絡中所有變量的聯合分布都可以因式分解為以其父變量為條件的單個密度函數的乘積。式（2）中的分子P（t［A］，t［E］），可以用式（3）來近似：

其中：父節點（Ej）表示Ej的父節點集。注意，由于所有屬性的值都是已知的，所以P（t［A］|parent（A））和P（t［Ej］|parent（Ej））是貝葉斯網絡中條件概率表（CPT）中的常量。當涉及式（2）中的分母P（t［E］）時，推理變得有點復雜。注意，P（t［E］）是證據屬性的邊際分布，可以通過邊際化查詢屬性上的聯合分布來計算，如式（4）所示。

P（t［E］）=P（A，t［E］）（4）

當同一元組t上存在多個缺失值的情況，每個查詢屬性Ai的分布通常不獨立于其他屬性。事實上，Ai的分布取決于其馬爾可夫毯中屬性的聯合分布。因此，提出在Ai的馬爾可夫毯的基礎上對Ai的域進行剪枝。具體地說，使用MB（A）表示A的馬爾可夫毯，且MB（A）=MB（A1）∪MB（A2）∪…∪MB（Ak）是所有查詢變量的馬爾可夫毯的交集。然后使用MB（A）中的證據屬性對A的域剪枝，即考慮與E∪MB（A）的值在數據集中同時出現的查詢屬性值。

算法1 不完整數據概率推理算法

在算法1中，輸入為關系模式R上的不完整數據集D，輸出為帶有概率的完整數據集D′。首先在不完整數據集D上訓練貝葉斯網絡，得到屬性之間的關系和概率表，并初始化查詢屬性集合Q、證據屬性集合E以及帶概率的完整數據集D′（第1、2行），判斷t［Ai］是否為空，并將空值屬性添加到查詢屬性Q中（第4、5行），其次查找Q中所有屬性的馬爾可夫毯屬性使其相交，得到共同馬爾可夫毯屬性MB（Q），并篩選出t［Ai］的所有可能填充的值V（第6～9行），然后將t［E∩MB（Q）］在D中至少出現一次的查詢屬性值添加到q_set，并利用式（3）計算P（t［E］）（第10～14行），遍歷V中屬性值利用式（2）計算P（t［Q］，t［E］）（第15～17行），最后計算P［ti］，將其和ti添加到D′中（第18、19行）。

3.3 相關性分析

本節介紹了一種基于卡方分布和Cramers V的方法，用于量化屬性之間的相關性，卡方統計量衡量了觀察值與期望值之間的偏離程度，當兩個屬性相互獨立時，卡方值接近于零。Cramers V是一種用于衡量兩個分類變量之間關聯性強度的標準化指標，派生自卡方統計量，其目的是使不同表格尺寸和自由度下的卡方統計量可進行比較。Cramers V值為0～1，數值越接近1，說明兩個變量之間的關聯性越強。卡方檢驗用于驗證分類變量之間的關聯性是否具有顯著性，而Cramers V則進一步提供了這種關聯性的強度度量。

定理1 在干凈數據集中，X→Y是一個FD，則Cramers V值為1。

當X和Y的頻數分布集中在一個單元時，會導致偏離程度較大。定理1解釋了隨機變量之間的相關性可以用Cramers V來表示，因此求解屬性之間的函數依賴關系等同于求解Cramers V的值，而這可以從觀察到的數據樣本中獲取。FD發現，問題可以看作是在屬性之間尋找強相關的屬性，當屬性之間存在強相關性時，則稱它們是一個函數依賴。通過計算屬性之間的關聯關系，而不是直接遍歷整個搜索空間，可以將函數依賴的發現問題簡化為尋找屬性之間的相關性。隨后，進行逐層搜索，從底層開始，即單個屬性節點，計算給定右部屬性與其他屬性的Cramers V值，并選取了大于給定閾值的屬性對作為候選的函數依賴項。為了提高挖掘效率，采取了剪枝策略，即排除相互獨立的屬性；當Cramers V值超過給定閾值時，將這兩個屬性視為強相關屬性，從而減小了候選函數依賴項的數量。

例2 圖2表示美國醫院數據集所有屬性之間的相關性分析熱圖，當ProviderNumber和HospitalName完全獨立時，總體上的分布和某個取值上的分布情況應該是相同的，當ProviderNumber和HospitalName完全相關時，也就是說， ProviderNumber的值就可以唯一地確定一個HospitalName，這就是Cramers V可能出現的最高值，也就是函數依賴關系。

3.4 候選FD規則驗證與細化

本節將詳細介紹對候選FD規則驗證與細化的過程，其目的是找到所有最小的函數依賴集合。當左部是多個屬性時，可以進行細化操作而不會引入額外的誤差。為實現這一目標，該過程執行以下步驟：首先，對于關系模式R的每個屬性A，尋找以A為RHS的最小AFDs。其次，計算屬性A與attr（R）＼A的每個屬性的Cramers V值。如果屬性A與某個屬性之間存在強相關性，確定該屬性為FD并報告它。如果屬性之間是中度相關關系，則將它們存入候選項中進行組合，直到無法從候選集中添加屬性。在此過程中，不斷剪枝相互獨立的屬性，并組合中度關聯的屬性，以確保找到的屬性集合都具有相關性。

在分析關系模式R時，每個候選RHS屬性A都需要被過濾，以確定是否有關聯關系。該過濾需要計算Cramers V值，以確定每個候選左部屬性是否適合作為FD的左部候選項。如果某個候選左部屬性被中度關聯的屬性作為細化候選，則可以使用算法2來執行細化，用于生成給定關系數據集D′的下一層級的FD。逐步增加屬性組合的規模，繼續計算它們之間的相關性，直到滿足閾值或不能繼續添加屬性。

算法2 候選FD規則驗證與細化算法

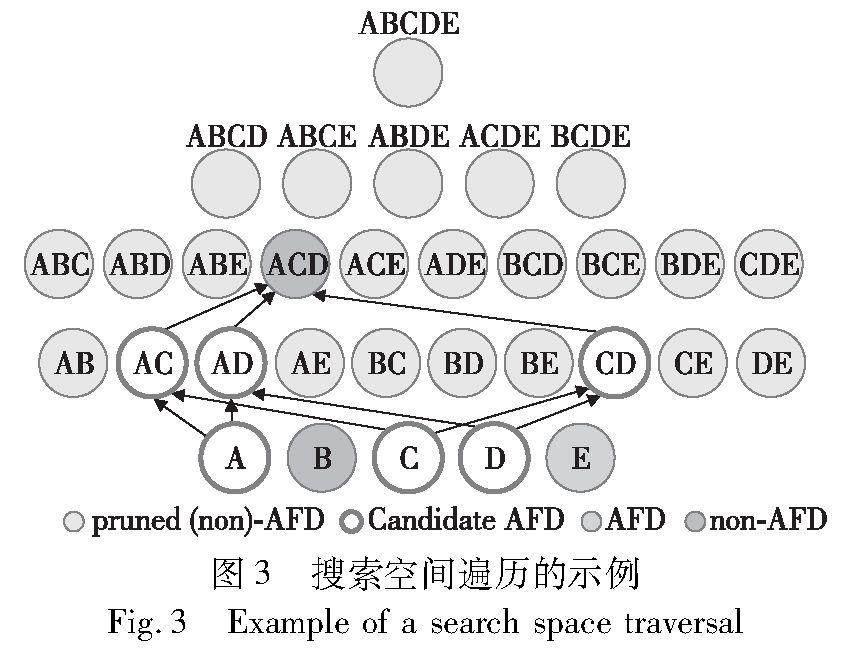
算法2接受一個帶有概率的完整數據集D′作為輸入，并輸出一組形式為X→Y的FD。在算法的開始，初始化一個用于存儲候選依賴項的新字典結構M以及一個空集合FD，用于存儲最終的FD集合（第1行）。接下來，算法遍歷關系模式R中的每個屬性，并針對每個屬性A遍歷attr（R）＼A中的屬性X（第2行）。通過調用函數計算X和A屬性之間的Cramers V（第6行），與上限閾值Vupper比較確保是一個FD，并將它儲存在集合FD中（第7、8行），例如圖2中的屬性B為依賴項，因此可以將B的超集剪枝。如果計算得到的Cramers V在上限閾值Vupper和下限閾值Vlower之間，則將屬性X添加到候選依賴項M中，就像圖2中的屬性{A，C，D}，只需要對中度關聯的屬性進行細化，這是潛在的最小依賴項，如果遞歸產生最小的函數依賴項，則會立即報告它。

對于候選依賴項進入細化部分，從候選依賴項M中選擇一個沒有被修剪的候選組合，向它添加M中單個屬性，組成一個沒有被修剪過的新候選項（第11行），在圖3中細化訪問的ACD是一個函數依賴項，并將它儲存在集合FD中（第14～16行）。如果錯誤地假設ACD是一個依賴項，將ACD添加到候選項M中，并繼續對ACD進行細化（第18行），直到無法從候選項中添加屬性，返回最終函數依賴項FD。與遍歷所有搜索空間相比，從單一屬性開始，對相互獨立的屬性剪枝，并對于中度關聯的屬性進行組合，大大減少了候選FD的規模。

例3 對于表1，當Stateavg作為右部屬性時，與State和 MeasureCode存在相關關系，且并非強相關性，將它們存入候選項中進行組合。通過驗證，確認{State，MeasureCode}與Stateavg為強相關關系，因此State，MeasureCode→Stateavg是一個FD。繼續驗證所有候選項，直到滿足預設閾值或無法繼續添加屬性。

4 實驗分析

本章通過實驗，評估了在不完整數據上挖掘近似函數依賴的方法，并展示了在合成數據集上的性能實驗結果。具體而言，本章將深入分析算法的準確率（P）、召回率（R）以及F1分數。

4.1 實驗設置

實驗采用Java實現了優化方法的編寫，命名為SFD，并與最先進的挖掘語義FD的方法FDX進行對比。

a）對比方法：FDX［20］是最先進的查詢有意義的函數依賴，從統計學角度出發，將FD發現轉換為線性結構化方程模型上的結構學習問題，在處理噪聲數據集時更具有魯棒性。參數保留其默認設置。

b）數據集：實驗數據使用合成數據集，給定一個具有r屬性的關系模式。考慮類別型和數值型兩種常見模式的函數依賴。對于類別型的FD，首先為LHS中的每個屬性分配一個域dom（X），并將RHS的域分配為dom（Y）。然后，對于每個值x∈dom（X）隨機選擇一個值y∈dom（Y）作為其對應的RHS值。如果LHS中有多個屬性，則將它們視為一個整體，并遵循與上述相同的流程。生成的樣本數量由分配給元組數量的參數t的值決定；對于數值型的FD，首先為LHS屬性分別分配一個域，dom（X1）和dom（X2）。屬性Y是FD的右部，使得X1+X2=Y。由于數值型函數依賴的可逆性質，X1+X2→Y、Y－X1→X2、Y－X2→X1也成立。

c）缺失值：使用Uniform和Pareto兩種模式，注入從5%到30%的缺失值百分比。在Uniform模式下，將隨機注入的缺失值均勻分布在屬性集上；對于Pareto模式，在80%的屬性中隨機注入20%的缺失值，在其余20%的屬性中隨機注入80%的缺失值。

d）實驗評價：為了評估算法對數據集檢測的準確性，實驗使用準確率（P）定義在所有識別的FD中正確檢測到的真實FD的百分比，召回率（R）定義在所有實際FD中正確發現的真實FD的百分比；而F1分數計算為2PR/（P+R），同時考慮了準確率和召回率。F1分數可以看作是模型準確率和召回率的調和平均值，最大值為1，最小值為0。

4.2 實驗分析

在本章實驗中，通過改變輸入數據的不同關鍵因素，評估了提出的不完整數據上的近似函數依賴挖掘方法和其他方法在合成數據集中挖掘FD的性能。

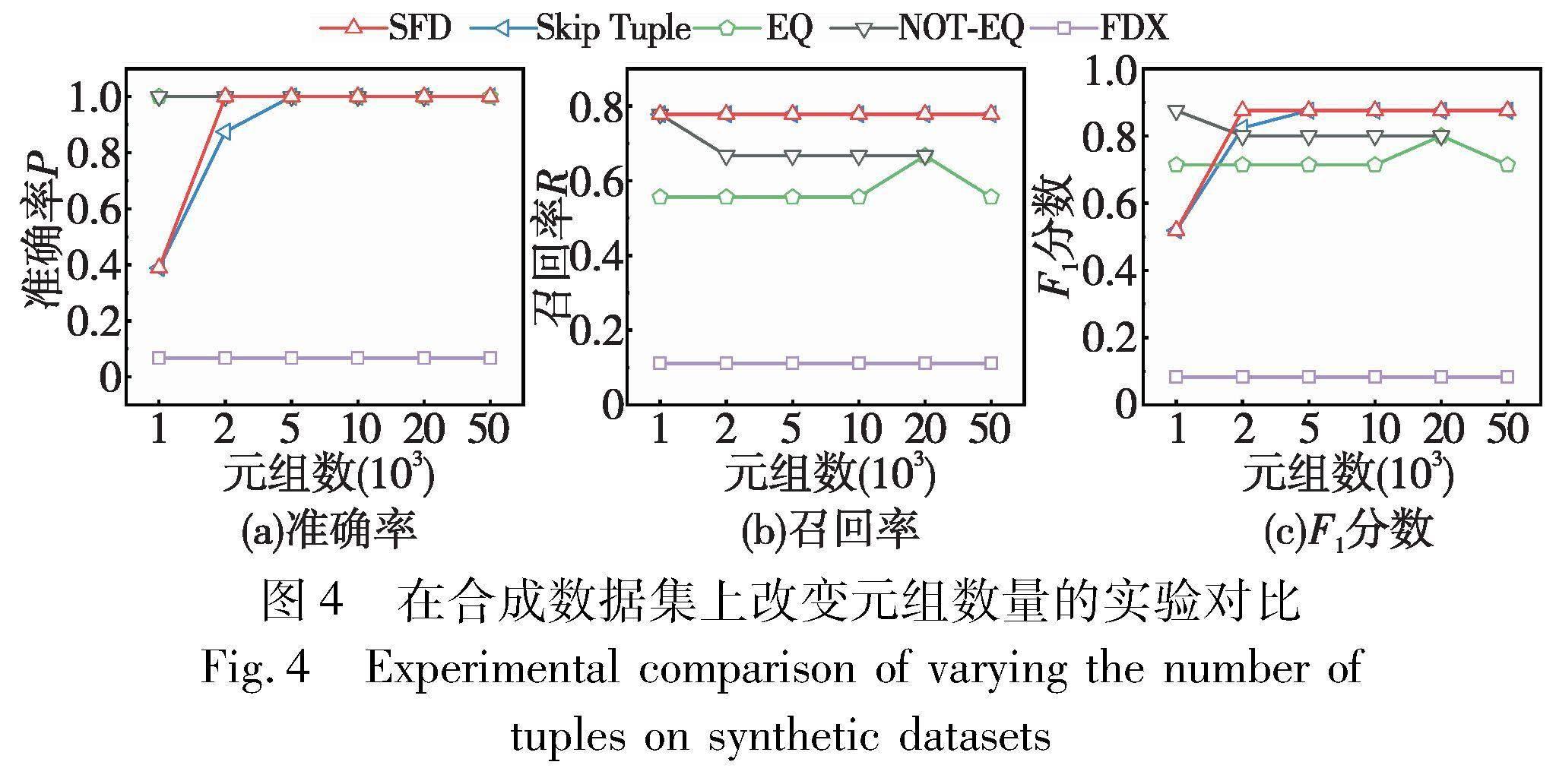
4.2.1 評估FD挖掘方法對元組數量的拓展性

實驗評估了元組數量對方法的擴展性，生成了一組合成數據集，并比較了不同元組數量下的性能。為了確定算法在行數上的可擴展性，使用了一個包含17列，缺失率為10%的合成數據集，在具有{1000、2000、5000、10000、20000、50000、100000}不同元組數量的數據集上進行了實驗，并在圖4中描述了結果。SFD在處理更多元組時展現出可擴展性，隨著元組數量的增加，在準確率、召回率和F1分數上呈現出更好的表現。同時，兩種缺失值語義和跳過缺失元組的變化相對穩定，相比之下，FDX無法識別具有環形結構的依賴，即同一屬性既出現在一個規則的左部，又出現在另一個規則的右部，導致準確率和召回率較低。

4.2.2 評估FD挖掘方法對缺失率的魯棒性

在Uniform模式下，實驗評估了缺失值的百分比對方法的影響。使用了一個包含17列，10 000行合成數據集，并隨機將與參與真實函數依賴的屬性對應的單元格翻轉為空值，以模擬高缺失率環境。通過控制“缺失率”設置來調整翻轉單元格百分比，并測量在{0.01，0.05，0.1，0.15，0.2，0.25，0.3}不同缺失率下各方法的性能表現。對比了兩種缺失值語義（⊥=⊥）和（⊥≠⊥），跳過缺失值所在的行與FDX方法，實驗結果如圖5所示，在高缺失率的情況下，所有方法都受到影響而性能惡化。SFD始終保持相對穩定且F1分數優于其他方法；對于兩種缺失值語義和跳過缺失元組，會挖掘出大量虛假的FD規則或錯過真正的FD規則，導致準確率、召回率和F1分數偏低。FDX總體上仍有非常低的準確率和召回率。

4.2.3 評估FD挖掘方法對缺失值分布的影響

現實世界中缺失值的分布通常是不均勻的，使用Pareto模式注入缺失值以模擬真實世界上的缺失值分布，如圖6所示。通過比較實驗結果發現，與Uniform模式相同，當缺失率過高時，所有方法的準確率、召回率和F1分數都會明顯降低。但提出的方法在F1分數上優于其他方法，并且在保持高召回率方面表現出色。由于FDX的列排序限制了屬性之間的優先級，無法挖掘具有環形結構的FD，可能會錯過一些依賴關系，導致無法完整挖掘到所有存在的函數依賴，使得準確率和召回率偏低。SFD通過基于相關性分析和概率模型的思想，更加靈活地捕捉屬性之間的關聯關系。

所提算法存在一些限制，其中最主要的限制是它無法發現數值型的FD。該算法專注于識別LHS和RHS之間的相關性，并且它不能進行逆向推導，找到數值型的函數依賴。然而，在實際應用中，用于數據清洗的函數依賴大多具有語義關系。未來的研究可以進一步完善算法，以更好地滿足實際數據清洗的需求。

5 結束語

本文提出了一種語義FD發現方法，探討了現有的函數依賴挖掘方法在面對缺失值和語義關系時的局限性。為了克服這些問題，本文提出了一種基于統計學的FD挖掘方法，考慮屬性之間的關聯性，并利用概率圖模型對不完整數據進行建模，可以在不完整數據上挖掘出有意義的函數依賴規則。利用屬性之間的關聯關系而不是遍歷所有的搜索空間來提高FD發現的準確率和召回率。測試表明，提出的方法在合成數據集上得到了高準確率和召回率。但當數據集中的缺失率較高時，存在大量缺失信息，使得通過概率建模難以準確捕捉屬性之間的真實語義關系。在處理大規模真實數據集時，算法的計算開銷較大。未來的研究可以致力于應對這些挑戰，優化算法以適應高缺失率情況，并尋找更有效的方法來處理大規模真實數據集。

參考文獻：

［1］Kruse S，Naumann F. Efficient discovery of approximate dependencies ［J］. Proceedings of the VLDB Endowment，2018，11（7）： 759-772.

［2］Berti-quille L，Harmouch H，Naumann F，et al. Discovery of genuine functional dependencies from relational data with missing values ［J］. Proceedings of the VLDB Endowment，2018，11（8）： 880-892.

［3］張安珍，司佳宇，梁天宇，等. 規則與概率相結合的不一致數據子集修復方法 ［J/OL］. 軟件學報，2023. https：//doi. org/10. 13328/j.cnki.jos.006972. （Zhang Anzhen，Si Jiayu，Liang Tianyu，et al. Subset repair method combining rules and probabilities for inconsistent data ［J/OL］. Journal of Software，2023. https：//doi. org/10. 13328/j. cnki. jos. 006972.）

［4］Zheng Zheng，Zheng Longtao，Alipourlangouri M，et al. Contextual data cleaning with ontology functional dependencies ［J］. ACM Journal of Data and Information Quality，2022，14（3）： 1-26.

［5］Song Shaoxu，Gao Fei，Huang Ruihong，et al. Data dependencies extended for variety and veracity： a family tree ［J］. IEEE Trans on Knowledge and Data Engineering，2020，34（10）： 4717-4736.

［6］Kaminsky Y，Pena E H M，Naumann F. Discovering similarity inclusion dependencies ［J］. Proceedings of the ACM on Management of Data，2023，1（1）： 1-24.

［7］Schmidl S，Papenbrock T. Efficient distributed discovery of bidirectional order dependencies ［J］. The VLDB Journal，2022，31（1）： 49-74.

［8］Fan Wenfei，Geerts F. Uniform dependency language for improving data quality ［J］. IEEE Data Engineering Bulletin，2011，34（3）： 34-42.

［9］Papenbrock T，Naumann F. Data-driven schema normalization ［C］//Proc of the 20th International Conference on Extending Database Technology. 2017： 342-353.

［10］夏秀峰，劉朝輝，張安珍. 基于馬爾可夫毯的近似函數依賴挖掘算法 ［J］. 沈陽航空航天大學學報，2023，40（4）： 8-18. （Xia Xiufeng，Liu Zhaohui，Zhang Anzhen. Approximate functional depen-dence discovering algorithm based on Markov blanket ［J］. Journal of Shenyang Aerospace University，2023，40（4）： 8-18.）

［11］Beskales G，Ilyas I F，Golab L. Sampling the repairs of functional dependency violations under hard constraints ［J］. Proceedings of the VLDB Endowment，2010，3（1-2）： 197-207.

［12］Huhtala Y，Krkkinen J，Porkka P，et al. TANE： an efficient algorithm for discovering functional and approximate dependencies ［J］. The Computer Journal，1999，42（2）： 100-111.

［13］Novelli N，Cicchetti R. Functional and embedded dependency infe-rence： a data mining point of view ［J］. Information Systems，2001，26（7）： 477-506.

［14］Hong Yao，Hamilton H，Butz C. FD-Mine： discovering functional dependencies in a database using equivalences ［C］// Proc of IEEE International Conference on Data Mining. Piscataway，NJ： IEEE Press，2002： 729-732.

［15］Abedjan Z，Schulze P，Naumann F.DFD： efficient functional depen-dency discovery ［C］// Proc of the 23rd ACM International Confe-rence on Information and Knowledge Management. New York： ACM Press，2014： 949-958.

［16］Flach P A，Savnik I. Database dependency discovery： a machine learning approach ［J］. AI Communications，1999，12（3）： 139-160.

［17］Lopes S，Petit J M，Lakhal L. Efficient discovery of functional depen-dencies and Armstrong relations ［C］// Proc of International Confe-rence on Extending Database Technology. Berlin： Springer，2000： 350-364.

［18］Wyss C，Giannella C，Robertson E. FastFDs： a heuristic-driven，depth-first algorithm for mining functional dependencies from relation instances extended abstract ［C］// Proc of International Conference on Data Warehousing and Knowledge Discovery. Berlin：Springer，2001： 101-110.

［19］Papenbrock T，Naumann F. A hybrid approach to functional depen-dency discovery ［C］// Proc of International Conference on Management of Data. New York： ACM Press，2016： 821-833.

［20］Wei Ziheng，Link S. Discovery and ranking of functional dependencies ［C］// Proc of the 35th IEEE International Conference on Data Engineering. Piscataway，NJ： IEEE Press，2019： 1526-153.

［21］Ilyas I F，Markl V，Haas P，et al. CORDS： automatic discovery of correlations and soft functional dependencies ［C］// Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press，2004： 647-658.

［22］Zhang Yunjia，Guo Zhihan，Rekatsinas T. A statistical perspective on discovering functional dependencies in noisy data ［C］// Proc of ACM SIGMOD International Conference on Management of Data. New York： ACM Press，2020： 861-876.

［23］Badia A，Lemire D. Functional dependencies with null markers ［J］. The Computer Journal，2015，58（5）： 1160-1168.

［24］Badia A，Lemire D. On desirable semantics of functional dependencies over databases with incomplete information ［J］. Fundamenta Informaticae，2018，158（4）： 327-352.