兩種高效局部搜索算法求解RB模型實例

楊易 王曉峰 唐傲 彭慶媛 楊瀾 龐立超

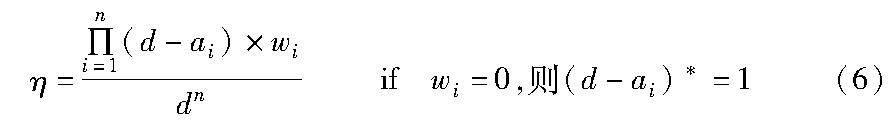
摘 要：RB （revised B）模型是一種在約束可滿足問題中具備精確相變增長域的隨機實例模型，提出兩種高效的啟發式局部搜索算法用于解決RB模型生成的大值域約束可滿足問題。首先為基于權重指導搜索的W-MCH算法，該算法通過約束判斷和違反約束數計分來進行搜索，并引入了基于約束違反概率的權重計算公式，根據其關聯的約束權重進行修正，再對變量進行迭代調整。然后提出最小化值域的MDMCH算法，該算法通過記錄違反約束和逐步消除已違反約束變量的啟發式策略來減少搜索空間，并在最小化后的變量域內重新校準變量賦值，進而有效提高算法的收斂速度。此外，還提出了融入模擬退火策略的WSCH和MDSCH算法，這兩種算法都能根據變量的表征特點對變量域進行針對性的搜索。實驗結果表明，與多種啟發式算法相比，這兩種算法在精度與時間效率方面均呈現明顯提升，在復雜難解的實例中能夠提供高效的求解效率，驗證了算法的有效性和優越性。

關鍵詞：RB模型；約束滿足問題；局部搜索算法；模擬退火；最小沖突啟發式

中圖分類號：TP301?? 文獻標志碼：A??? 文章編號：1001-3695（2024）05-017-1394-08

doi： 10.19734/j.issn.1001-3695.2023.09.0415

Two efficient local search algorithms for solving RB model examples

Abstract：The RB （revised B） model is a stochastic instance model with an accurate phase change growth domain in constraint-satisfiable problems. This paper proposed two efficient heuristic local search algorithms to solve the large-value domain constraints generated by the RB model. The first is the W-MCH algorithm based on weight-guided search. This algorithm searched through constraint judgment and constraint violation score， and introduced a weight calculation formula based on constraint violation probability， which was modified according to its associated constraint weight， and iteratively adjusted then variables. Then it proposed the MDMCH algorithm for minimizing the value range， this algorithm reduced the search space by recording the heuristic strategy of constraint violations and gradually eliminating the violated constraint variables， and recalibrated the variable assignments within the minimized variable domain， thereby effectively improving the algorithms convergence speed. In addition， it also proposed the WSCH and MDSCH algorithms that incorporate simulated annealing strategies. Both algorithms can perform targeted searches in the variable domain based on the characterization characteristics of the variables. Experimental results show that compared with various heuristic algorithms， these two algorithms have significantly improved accuracy and time efficiency， and can provide efficient solution efficiency in complex and difficult instances， verifying the effectiveness and superiority of the algorithms.

Key words：RB model; constraint satisfaction problem; local search algorithm; simulated annealing; minimum conflict heuristic

0 引言

約束可滿足問題（constraint satisfiability problem，CSP）作為人工智能科學領域的一個關鍵研究方向，在實際優化問題中具有重要地位。許多現實世界中的優化難題都能以CSP形式建模，這使得CSP通過不同編碼方式的可滿足性判定問題（satisfiability，SAT）公式相對于隨機SAT公式更自然地刻畫了約束之間的關系。約束編程在諸如機器設計［1］、電路設計［2］、汽車變速器設計［3］、調度與規劃［4］等領域得到成功應用。因此，對CSP的深入研究變得愈加意義非凡。在CSP的生成模型、可滿足性相變和求解算法等方面，學者們都展開廣泛探討。最初，Achlioptas等人［5］發現了CSP的A、B、C、D四種初始模型存在嚴重缺陷，隨著變量數量的增加，并沒有出現漸進性的相變現象，即平凡漸進不可滿足性。為了彌補這些傳統模型的不足，E模型［5］和廣義模型［6］相繼被提出。然而，E模型無法靈活地調整實例的密度，而廣義模型則在引入概率分布后變得復雜。隨后，Xu等人［7］在2000年提出了一種新的隨機CSP模型，名為RB（revised B）模型。RB模型以其精確的相變特性，成為了一種增長域實例模型，完美地彌補了前述模型的不足。此后，Fan等人于2011年在RB模型基礎上提出了K-CSP［8］和d-K-CSP［9］兩個改進模型。趙春艷等人［10］則提出了p-RB模型。盡管這些模型都是基于RB模型的改進，但都存在一定的局限性。Huang等人［11］通過一階矩方式，推導出以RB模型生成的Max-CSP和Min-CSP的上下限。Xu等人［12］采用嚴格的一階和二階矩方法，證明了在可解階段接近可滿足的轉變，解會以指數數量的良好分離簇的形式聚合，每個簇包含亞指數數量的解，呈現出了聚類動態躍遷，而不是凝聚躍遷。最近，Zhou 等人［13］研究了模型RB的強制實例空間，并嚴格地證明了RB實例強迫解的期望數目與非強迫解的期望數目漸近相等。Xu等人［14］探究了RB模型解空間的結構，發現隨著約束密度的增加，模型呈現出獨立相變、聚類相變、可滿足性相變以及隔離相變四種相變特性。RB模型因其兼具上述模型的優點并彌合其缺陷，被廣泛應用于該領域。然而，RB模型生成隨機實例的求解難度在變量規模達到僅為102量級時變得極具挑戰性［15］。綜上所述，RB模型在CSP研究中扮演著重要角色，為該領域的研究人員提供了一種常用且多特性的隨機實例模型。

針對RB模型生成的大值域CSP實例的求解方法可以分為兩大類。首先是完備性算法，例如回溯技術、約束傳播和變量排序啟發式，這些方法雖然能確保解的準確性，但在處理大規模的RB模型實例時，時間復雜度呈指數級增長；其次是不完備性算法，包括局部搜索、自然啟發式和近似概率求解。雖然這些方法可能無法獲得精確解，但它們旨在可接受的時間內尋找近似解。2016年，王曉峰等人［16］探究了置信傳播算法在RB模型上的收斂性。同年，Xu等人［17］研究了局部搜索算法，提供了隨機游走算法的閾值界，并給出了隨機游走結合最小沖突啟發式算法。此外，2017年，原志強等人［18］引入了基于模擬退火的改進方法RSA（revised simulated annealing algorithm）和結合遺傳算法的GSA（genetic simulated annealing algorithm），用于求解RB模型實例。2018年，Bouhouch等人［19］將二元CSP建模為0-1二次規劃，提出了基于離散化神經網絡和局部搜索最小沖突啟發式MCH（minimum conflict heuristic algorithm）啟發式的方法，用于求解RB模型生成的二元CSP實例。2022年，Tnshoff等人［20］提出了一個可以訓練的通用圖神經網絡架構作為任何約束滿足問題的搜索啟發式方法，通過實驗證明該方法優于神經組合優化。同年，Korani等人［21］提出兩種離散群智能算法離散母樹優化（mother tree optimization，MTO）和離散的粒子群（discrete particle swarm optimization，PSO）求解RB模型生成的CSP實例。2023年，Hossain［22］根據CSP的約束條件對所有變量進行變量排序的啟發式策略，求解CSP實例。

本文基于RB模型生成的CSP問題實例，對CSP中的最大約束可滿足問題（MAX-CSP）的求解算法進行了深入研究。主要關注局部搜索算法，并提出了兩種高效的局部搜索算法：基于權重搜索的W-MCH（weight-based minimum conflict heuristic algorithm）局部搜索算法和最小化變量域的 MDMCH（minimizing variable domain-minimum conflict heuristic algorithm）算法。通過收斂性和求解效率等實驗結果的驗證，這兩種算法各自展現了獨特的優勢。相較于MCH和WMCH（random walk minimum conflict heuristic algorithm），這兩種算法在收斂性上有了顯著提升。此外，在兩種局部搜索的基礎上提出了融入退火策略［18］的變體WSCH（weight-based simulated annealing minimum conflict heuristic algorithm）和MDSCH（minimizing variable domain simulated annealing minimum conflict heuristic algorithm）算法。而與文獻［17，18］中提到的RSA、GSA、WMCH等啟發式算法相比，這兩種算法在各變量規模上的求解時間至少縮短了30%，且在減少不可滿足約束數方面取得了顯著進展。與多組啟發式算法相比，實驗結果表明，這兩種局部搜索算法在求解RB模型生成的CSP實例時，呈現出高效的求解效率。

1 RB模型

RB模型是從著名的CSP模型B改進而來，RB模型的一類隨機CSP實例表示為P∈RB{k，n，α，r，p}，其中對于每個實例的符號定義［11］如表1所示。由表1定義可以看出，隨著RB模型變量數xn的增長，取值域dn規模是呈多項式級增長。生成一個實例P∈RB（k，n，α，r，p），具體步驟如下：

a）設置模型RB的主要參數n、p、α和r。其中n是變量數量，p是約束緊度，r和α是兩個自定義的常數。

b）重復隨機選擇m個約束條件，每個約束都是通過從n個變量中獨立隨機地選擇k個變量形成。

c）對于每個約束C，從完整的dkn個賦值中隨機選取pdkn 種不同的k元賦值，形成一個不相容賦值的集合Qa，當約束C的變量取值不屬于這些不相容賦值集合Qa時，該約束滿足。

在文獻［23］中給出控制參數p，臨界值pcr，可確定RB模型的可滿足性相變現象，并給出以下定理。

利用上述定理公式，根據RB模型的參數取值可確定出相變點pcr。更準確地說，變量數接近無窮時，若ppcr，則CSP實例高概率接近0，無解。

2 局部搜索算法

2.1 MCH算法

局部搜索是解決約束滿足問題復雜計算組合問題的基本范式之一。盡管系統、完整的搜索算法已經取得了進步，但在大多情況下，局部搜索方法是解決這些大型復雜實例的優秀可行方法。在解決CSP時，傳統的局部搜索算法通常從一個初始解s出發。在算法的迭代過程中，它會反復在當前解的鄰域（s） 中尋找比當前解更優的解，并將找到的更優解替代當前解s*，直到在當前鄰域（s）中無法找到比當前解更好的解為止。如果在整個搜索過程中無法找到比解s*更優的解，則該解被視為局部最優解。

MCH迭代地修改單個變量的賦值，使違反約束的數量最小化。假設給定一個CSP實例P，通過為P中的每個變量賦值來初始化搜索過程，該值是從其域中統一隨機選擇的。在每個局部搜索步驟中，首先從沖突集中均勻地隨機選擇一個CSP變量x，然后從x的值域中選擇一個新值d，將d賦值變量x，使不滿足的約束沖突的數量最小化。如果有多個具有該屬性的沖突變量x值，則隨機選擇。當找到解決方案或超過搜索步驟數限制時，終止搜索。這種傳統的局部搜索策略在尋找解決CSP的最優解時，一般都是通過持續地在搜索空間中尋找更優解，逐步單個地改善當前解，以達到更好的問題解決效果。MCH求解RB模型實例的偽代碼如算法1。

算法1 MCH算法

2.2 W-MCH算法

與MCH算法不同，基于約束權重的概率選擇變量賦值的W-MCH算法是一種可變深度搜索策略，同時引導多個變量的搜索過程。在這一算法中，首先仍以CSP問題的違反約束記錄值作為算法的求解評價標準，即評估函數。對于RB模型實例，一組賦值解為X={x1，x2，…，xn}，對該組賦值進行約束檢查，若違反約束時標記1分，否則計0分。通過對一組賦值進行約束檢查并計算評估分值，MAX-CSP問題的目標在于最小化評估函數的目標分值S，具體函數如下所示。

其中：m為約束的數量，通過檢查賦值是否滿足約束集Cm，使得評估分值S為0或最小，特別是在處理復雜實例的可滿足相變區域時，求解算法的主要目標是在合理的時間范圍內尋找到違反約束最少的解。

當k=2，n=3，α=1，r=2，p=0.25時，考慮圖1中的RB模型實例P（k，n，α，r，p）。圖中綠色圈中，表示變量X={x1，x2，x3}，而紅色框中（參見電子版）表示的是變量約束，由r×n×ln n可得出約束數m為7，則約束C={c1，c2，…，c7} ，每個變量x映射的dn域大小為nα，計算結果為3，即值域d={0，1，2}，圖1中下方為不相容賦值Qa。W-MCH算法開始于隨機初始化多組解，并為每組解進行評估得分。隨后，記錄初始賦值中得分最低的解，記為sol。假設初始解為sol={1，1，0}，接下來進行約束檢查，以c1約束為例，涉及變量（x2，x3），當x2賦值為1，x3賦值為0時，檢查其約束對應的不相容賦值Q1={（1，2），（2，2）}，可以發現約束c1是滿足的，如圖1用實線表示滿足約束。依次檢查完所有的約束，在此實例中，初始解sol={1，1，0}違反約束c2、c3、c5，如圖1用虛線表示。同時，在檢查的過程中，初始化一個變量索引數組，記為C_values，在索引數組中存儲其違反約束的變量索引，如違反約束c2的變量對應索引值為（1，2），累計存儲在C_values數組中。

此時，在MCH算法中的做法是記錄違反的不相容賦值中的Q，記為沖突集，對違反的單個變量進行賦值修改。然而當實例復雜時，MCH算法在單個變量上的修改可能效果有限。相比之下，W-MCH算法采用一種基于權重的方法，不同于MCH的是，W-MCH以C_values變量索引數組尋找其違反約束值，在每次循環中對賦值sol，通過權重指導實現多變量修改的算法策略。分析得到的索引變量集C_values，在該數組中發現索引的次數恰好代表了其變量的違反次數，故可對C_values進行統計排序，并對應地計算在數組中的占比概率pi。

pi=C（indexicount）/C_valueslength（4）

其中：C（indexicount）表示對應索引值的計數頻次；C_valueslength為索引數組長度。事實上使用頻次計算出頻率pi或者其他概率，并不能有效地進行概率選擇。原因是隨著變量的增加，單純的概率值并不能完全反映出變量的優劣程度。如C_values中最大的P1 =0.5，但實際C_values數組中的x1已是最差的賦值變量。需要將概率值進行映射以便更好地表征好壞程度，或者按照概率值的大小給予不同的權重來進行選擇，對此提出了以下的權重公式。

其中：s=0.05為一個常數，控制著權重公式與映射曲率的大小，圖2為s取不同數值對其曲率的影響。由于s參數控制權重值的大小，又因在上述公式中，若indexicount值越大，表明當前的賦值違反約束的數量越多，違反概率也相應增大，所以需要更大的權重值來調整當前賦值中的差值變量。理論上，當存在概率值時，都必須修改違反約束的變量，然而變量之間的相互約束，必須固定一部分違反約束較少的賦值變量，對于違反約束多的賦值，使之以更高的權重去修改變量賦值。然而整體權重值不能過大，以免導致算法過于隨機化。經過多次實驗和分析，取參數值s=0.05。由于權重值是以約束的違反概率進行計算的，所以并不會影響變量修正的準確性，可以看出，隨著變量數的增加，C_valueslength的違反約束數也會增加，當indexicount=0，即違反約束為0時，權重也為0，而當約束違反時，權重也會隨之增加。但當變量增多時，整體的權重值在迭代修正后會陷入一個局部值，從而影響算法的收斂速度。利用此策略得到一組最優賦值后再利用MCH算法，所以此操作并不會影響算法的準確性。如在圖1 C_values中，變量x1的賦值違反約束頻次為index1count=3，同理index2count=2，index3count=1，代入上述公式可以計算出weight1=0.99，weight2=0.96，weight3=0.56。以此權重對sol的所有變量重新賦值，假設賦值x1=2，x2=0，x3未能修改，則得到的解為solbest={2，0，0}，重新檢查約束集，則只有c3和c6違反，重復上述操作即可有效地降低算法的違反約束。

從圖2中可以看出，實際上在當Pi>20% 時，權重已經大于0.6，能滿足大多數違反變量的修改，在實際操作中若以weight>0 時的權重賦值，會造成算法過于隨機化，導致算法不能有效收斂。當weight為0.3左右時，變量的原始概率值基本處于5%之上，為了使初始權重大多數變量都能被優化，則取weight>30%為每次迭代的賦值概率。

Q1={（1，2），（2，2）}，Q2={（0，0），（1，1）};

Q3={（1，1），（2，0）}，Q4={（2，1），（1，1）};

Q5={（1，0），（2，2）}，Q6={（0，1），（0，0）};

Q7={（1，2），（2，1）}

C_values=［1，2，1，2，1，3］

為了驗證以上取值，分析算法的權重初始值與迭代后的權重值。在圖3中可以看出變量數n=100，在經過200次迭代計算，得到的藍色區域（參見電子版）為迭代后的權重與初始權重的差值，可以看到，經過權重指導搜索后，絕大多數變量的權重已經小于初始權重值。此操作可以根據權重的不同分配，對不同的概率值造成不同程度的影響，從而實現根據權重調整的效果。經過權重調整后，可以得到一組優秀賦值解，再以MCH算法逐步搜尋單個變量進行修改。W-MCH算法的偽代碼如算法2所示。

算法2 W-MCH算法

2.3 MDMCH算法

若能以高效策略為MCH算法提高一組出色的起始賦值，那么在相變區域內或許將獲得優越的可行解。在分析W-MCH算法的權重圖之后，可觀察到在迭代之末，大約有20%的權重值仍保持較高水平。然而，對于這些過于突出的權重值，有時一個變量可能違反多個約束。為解決這一問題，引入MDMCH算法，此算法基于權重思想構建，旨在通過消除違反約束的變量，從而有力地縮減搜索空間。

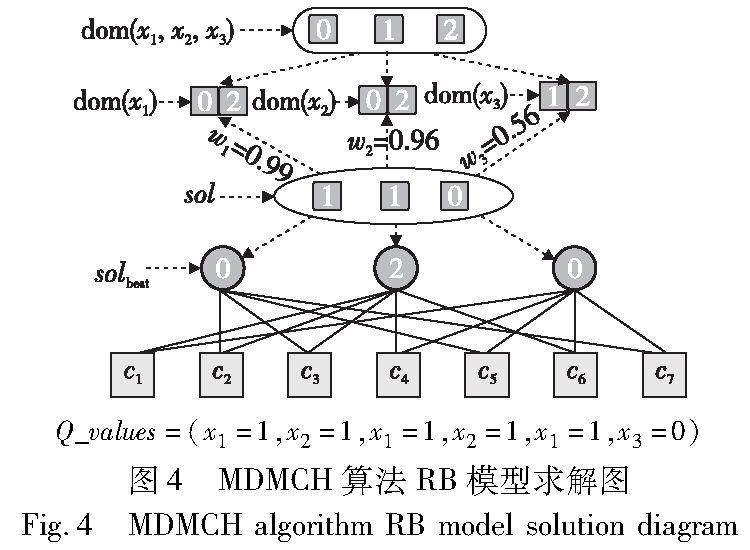
首先同W-MCH算法初始步驟基本一致，先進行初始的約束檢查，記錄C_values數組，同時記錄沖突變量集Qc，但MDMCH算法對于沖突集Qc的處理方式與MCH算法不同，MCH是在沖突集Qc中隨機選擇變量進行變量修改，最小化沖突數量。而MDMCH算法是在沖突集中尋找變量對應的違反變量值，然后將尋找出的變量與變量值累計存儲到Q_values數組中。如圖4所示，假設現在初始賦值還是sol={1，1，0}。可檢查出每個變量的違反約束值，在該組賦值中，x1、x2、x3三個變量取值都與約束沖突。然后將沖突值依次在各自的變量域中消除沖突的變量，分別得到變量域dom（x1）=（0，2），dom（x2）=（0，2），dom（x3）=（0，1），再利用權重公式進行指導搜索。通過權重值和消除后的各個變量域，可計算出此操作后的搜索空間為2×0.99×2×0.96×2×0.56≈4.25，而最初的基本搜索空間為33，此實例中搜索空間降低了85%。假設變量數為n，對應的變量域為d，而對應每個變量域消除的沖突變量數為ai（a∈d－1），每個對應的修改權重為wi，可計算出最小化值域與搜索空間dn的有效比值，計算公式如下：

若以各自的權重得到新賦值solbest={0，2，0}，并未違反約束進而高效地尋找出可行解。在最小化值域的策略中，每次消除的變量都是在隨機初始賦值的基礎上找出違反約束的賦值變量進行消除。每次消除違反賦值變量后，在剩余的值域內進行重新賦值。顯然，由于變量之間的相互約束性，此操作一定會過于刪除搜索空間，導致無法針對性求解，但會加快尋找局部最優解的速度；然而在簡單易解實例上，容易陷入局部最優；相反，在難解實例上，能高效地降低違反約束數，但在迭代后期也會陷入局部最優。雖然最小化值域的策略充分地減少了搜索空間，導致無法精確求解，但此操作的目的并不是最終求解，而是快速地得到一組較優賦值，在此賦值的基礎上再利用MCH算法在整個搜索空間進行針對性的精確搜索，不但不會影響MDMCH算法的精確性，反而這一策略加快了算法的收斂速度。由于在循環消除變量域的過程中，此操作無法考慮多組變量之間的約束相互影響的變量域，所以當變量增加時，在實驗中發現變量域中會被消除為空，這也是導致在此操作陷入局部最優的一個原因，這時取當前變量域中違反約束最小的賦值解，記為當前最優解。對此，以0.2的概率對變量域為空的變量在其原有的變量域中進行隨機賦值，跳出局部最優值，然后進行MCH算法的單個變量尋優。最后，通過權重差值實驗發現，同樣對100個變量進行200次迭代，分析初始權重，與迭代末的權重進行對比。權重值的優化如圖5所示，可以看出，MDMCH算法只有極個別權重值超過了初始權重值，對于大多數權重值都進行了優化處理。該操作利用最小化變量域的方式，極大地增強了算法的局部搜索能力。MDMCH算法的偽代碼如算法3所示。

算法3 MDMCH算法

2.4 WSCH與MDSCH算法

由于在后期的搜尋中，基于權重和最小化值域的兩種算法策略都會縮小搜索空間，陷入局部最優，而MCH算法的收斂效果較差。故而在W-MCH與MDMCH迭代后尋得一組最優賦值，可融入模擬退火策略的MCH算法再進行尋優，并以1-3/T的概率進行選擇擾動，利用最小約束數及當前退火溫度T以 exp［－（Fnow－Fbest）］ 概率來接受新的賦值，在退火初期，需要使賦值進行擾動后接受新賦值的概率較大。此賦值在大范圍的賦值空間中對變量賦值能夠進行隨機擾動。在退火后期，隨著T值的減少，擾動概率減小，則對較優賦值進行針對性擾動。這樣在求解實例時，開始退火時期算法有優秀的能力來逃避局部最優值，從而快速找到簡單實例解。在求解復雜實例時，前期雖然過于隨機化，但隨著退火溫度的下降，算法在退火后期又可以進行針對性的尋優。避免以傳統退火策略中盲目性的隨機擾動降低求解效率，以此來提升算法的求解精度。引入退火策略算法具體的WSCH與MDSCH偽代碼如算法4。

算法4 WSCH、MDSCH算法

2.5 算法時間復雜度分析

兩種改進的局部搜索策略中都涉及到了約束檢查與后續MCH算法的尋優，對此首先分析約束檢查的時間復雜度，在W-MCH算法迭代的主循環內部會依次遍歷其約束數m，則時間復雜度為O（m）。對于內部約束檢查中每次在解sol中取出k個變量x的時間復雜度為O（k） ，然后將取出的變量與每組約束C中的t個具體約束集進行判斷的時間復雜度為O（t），該操作的時間復雜度為O（m×k×t）。即約束檢查的時間復雜度為

T1（m，t，k）=O（m×t×k）（7）

而約束數r×n×ln n=m，pdkN=t，dN=nα，則T1為

記錄索引數組與權重計算涉及的操作相對較少，從約束集中取出不滿足約束索引為O（k），而對于C_values數組索引排序的最大操作時間復雜度為數組長度，與賦值操作都為常數級。

MCH算法的時間復雜度主要取決于兩個因素。首先是算法的迭代次數，算法通過迭代多次來尋找解，迭代次數可以通過設置參數來控制。通常情況下，迭代次數與問題的規模和復雜性無關，因此可以視為常數。其次是單次迭代中的局部搜索復雜度和沖突減少的效率與具體問題局部搜索實現算法相關。

綜合考慮以上因素，最小沖突啟發式算法的時間復雜度可以表示為

T2（n）=O（f（n，M，m））（9）

其中：n為問題規模；M為迭代次數；m為局部搜索的復雜度，而MCH的局部搜索主層循環時間復雜度為O（maxSteps），內部搜索操作的搜索復雜度和沖突減少的效率主要取決于循環中約束檢查不滿足變量的時間復雜度T1，而對于每次變量修改的時間復雜度為O（k），所以MCH的時間復雜度為

T3（maxSteps，T1）=O（maxSteps×T1×k）（10）

MDMCH比W-MCH算法多一步消除變量域的中間處理操作，實際處理的主要時間復雜度為O（nα），而nα為變量域的大小，為常數級。兩種局部搜索的主要時間復雜度都為

WSCH與MDSCH算法外層循環主要為降溫次數，時間復雜度為O（log（T0/T）） ，內層循環為嘗試產生新的解并決定是否接受新解，主要的迭代次數由馬爾可夫鏈長度L參數控制，約束檢查與上述復雜度T1一致。兩類變體算法的主要時間復雜度為

T5（T0，T，L，T1）=O（log（T0/T）×L×T1×k）（12）

由于RB模型為二元約束，k為常數取2，其中α取0.8，r和約束緊密度P為常數。即當RB模型參數確定時， 兩種局部搜索W-MCH、MDMCH與兩種退火策略的WSCH與MDSCH變體算法的主要復雜度為T=O（n×ln n）。

3 實驗分析

為了驗證基于權重和最小化值域兩種算法策略的效率，分別進行了收斂性與求解概率實驗。此次實驗取文獻［17，18，24～27］中參數明確，且為同類型的隨機啟發式算法作為對比實驗。實驗環境為Windows 11，64位操作系統，CPU為AMD Ryzen 7 5800H，主頻為3.20 GHz，內存16 GB；RB模型參數取與文獻［18］中相同的參數，k=2，α=0.8，r=3，n=［20∶20∶100］由定理1計算，可滿足性相變點為Pcr=0.234。對于不同的n取約束密度p=［0∶0.01∶0.2］，由上述數值生成的RB模型的具體參數如表2所示。

3.1 收斂性分析

首先，對W-MCH、MDMCH與MCH，和文獻［17］中隨機游走最小沖突啟發式WMCH算法的收斂曲線進行對比分析。隨后與文獻［18］中RSA和GSA算法進行收斂曲線對比，而GSA和RSA算法都是以退火策略為循環。由于迭代次數與RSA和GSA不一致，為了方便比較，實驗的收斂性比較以時間為橫軸。

在圖6（a）～（d）中，分別展示了這四種算法隨著變量數和約束密度的增加，其收斂曲線的變化趨勢。在圖6（a）中，展示了變量數n=20 以及約束密度p=0.14時的收斂曲線。在這種情況下，WMCH表現出最佳的收斂性能。這歸因于隨機游走搜索方法的盲目性，使其在簡單實例上尋找可行解空間時的表現較優。盡管期望步數在隨機給定初始分配后非常大，即（1-p）-rnln n，但WMCH在一定概率下執行隨機游走，具有一定程度跳出局部最優的效果，因此，在較為簡單的實例中，WMCH的優越性明顯。而W-MCH與MDMCH表現一般，由于在本身策略下縮小解空間，得到的一組較優賦值后再由MCH算法處理，與MCH、WMCH在簡單實例上隨機賦值相比有一定的隨機性，當WMCH與W-MCH和MDMCH的初始賦值違反約束數相差不大時，相對于WMCH與MCH，W-MCH與MDMCH增加了算法的復雜度，故收斂性較差。

不過隨機實例的復雜性上升，在n=60，p=0.14時，兩種局部搜索的搜索優勢體現出來，在圖6（b）中可以看到，W-MCH的收斂速度最快，在100次迭代后，最小不可滿足約束數相對比于MCH、WMCH與MDMCH至少降低了34%左右。而WMCH有一定概率的隨機游走步驟，在實例稍復雜時，則是四種算法中收斂速度最差的。值得注意的是，在較復雜的實例中，MDMCH算法的效率與MCH、WMCH相當，這是因為其中違反約束的數量相對較少，約束密度較小導致的不相容賦值稀疏，indexicount 違反的頻次與C_valueslength的比值較小，處于一個權重低位值，然而此實例下也不是難解實例，復雜約束較少，故最小化值域策略的效果不明顯。

進一步增加模型實例的復雜度，當n=100和p=0.14 時，兩種局部搜索方法的收斂速度顯著增快，如圖6（c）所示，大約在50次迭代后，這兩種方法的最少不可滿足約束數位于［40，60］，而MCH和WMCH算法的最少不可滿足約束數則在［130，140］。在相同的迭代次數下，相對于其他三種算法最少不可滿足約束數至少降低了70%。在此實例下，MDMCH算法的優勢十分明顯，其最小化變量域的策略有助于更快地獲得一組初始賦值，加快算法的收斂速度。此外，隨著實例的復雜程度增加，似乎在接近實例的可滿足相變點附近，MDMCH算法更具有快速收斂的趨勢。對于最具挑戰性的實例，即n=100和p=0.20 的情況下，復雜約束增大，如圖6（d）所示，MDMCH算法在難解實例上的收斂速度最佳，這是由于無論算法處于哪種實例，在每次迭代求解中，C_valueslength 為一次約束檢查數組長度的定值，然而當實例復雜時，即weight 與indexicount成正比，若賦值變量的違反約束數越大，則導致該變量的indexicount越大，則權重的值也相應增大，故而在復雜難解實例上算法的收斂速度越快，而實例簡單時，該值影響的權重值較小，故而收斂速度無難解實例上那樣明顯，但由于變量約束的相互影響，又不能將概率權重映射過度放大，會造成多組賦值變量都需要以高權重進行修正，導致算法難以收斂，而該組實驗的收斂圖像正好驗證了筆者的預期。需要指出的是，MDMCH算法引入了0.2概率的隨機賦值策略，從而在對比實驗圖（b）～（d）中復雜實例上的MDMCH算法的最少不滿足約束數最小。

圖6（e）（f）分別為n=60，p=0.14和n=100，p=0.14引入退火策略的兩種算法與GSA和RSA算法的時間收斂對比。可以看出，融入基于權重搜索和最小化值域搜索策略的WSCH與MDSCH算法能迅速收斂到局部最優值，在圖6（e）中兩種算法在10 s之內已達到個位數的最少不可滿足約束數，比其他兩種算法的時間效率最高提升70%，進而有效地給退火策略的MCH提供一組有效賦值，能盡早地搜索最優解。隨著實例的復雜度增加，在圖6（f）中，WSCH與MDSCH算法的收斂速度似乎更加明顯，而MDSCH相比于其他三種算法能更早地跳出局部最優，收斂速度大幅提升。此實驗中更加清晰地驗證了兩種改進方法對于變量迭代修正的效率遠遠高于RSA、GSA、MCH和WMCH改進算法。

3.2 求解效率對比分析

圖7中分別對比WSCH、MDSCH算法與RSA、GSA在RB模型各維度10組實例上的求解概率。圖7（a）～（d）分別展示了RSA、GSA、WSCH和MDSCH四種算法在不同約束密度下的收斂概率。其中RSA在p≤0.07時，GSA在p≤0.1時兩種算法在各組RB模型變量實例上以概率1收斂，W-SCH在p≤0.11時以概率1收斂，而MDSCH在p≤0.12時可有效求解。在低維實例上n為20、40時，WSCH表現出最佳的求解效率，在相變區域內依然有高概率可解，其次為MDSCH，在變量n取20，WSCH和MDSCH算法求解概率的約束密度p都達到了0.16，RSA與GSA算法分別為0.1和0.13。WSCH和GSA算法在臨近相變點0.20時依然有0.1概率求解，但求解概率高于GSA。在變量n取40時，MDSCH在p取0.14，0.15 時，求解概率分別為0.9和0.5，WSCH求解概率都為0.6，RSA和GSA算法分別在p取0.14和0.15時失效，而MDSCH和WSCH算法的求解概率分別達到了0.16和0.17。綜上分析，在低維實例上，WSCH稍優于MDSCH，兩種算法都優于RSA和GSA的求解效率。隨著實例變得復雜，MDSCH的求解能力在n取60、80、100的高維實例上體現了出來。在n為60時，WSCH在p=0.15 有0.1的概率收斂，而MDSCH算法有0.5的概率收斂，RSA和GSA求解失敗。在n取80時，WSCH在p=0.14有0.3的概率求解，RSA和GSA均已失效，而MDSCH依然有0.6的高概率求解。MDSCH在n取100時，將求解概率的約束密度提升到了0.12。綜合分析實驗結果，相比于其他三類算法，MDSCH在高維復雜實例上表現出色，其求解概率均高于對比算法，與此同時，WSCH在低維實例中表現出了良好的性能。

圖8中對比了四種算法在不同變量規模下的總運行時間。可以觀察到，每個規模下MDSCH和WSCH算法的總運行時間都明顯優于GSA和RSA算法，時間效率最大提升了50%左右。值得注意的是，隨著變量規模的增加，尤其是在復雜可解實例中，MDSCH的時間效率開始優于WSCH算法，MDSCH的最小化值域策略開始發揮作用，這使得它能更快地為退火策略的MCH算法提供一組出色的賦值，從而提高了求解的時間效率。綜上所述，MDSCH和WSCH算法在不同規模的變量下都表現出良好的性能，特別是在高維度和復雜實例中，MDSCH算法在求解效率方面表現出色。

為了進一步驗證WSCH和MDSCH算法的有效性，圖9（a）（b）分別在變量n取80、100，約束密度為［0.11，0.17］，進行50個隨機實例的求解概率對比。其中BP-RSA-1（belief propagation-revised simulated annealing algorithm-1）［24］、 BP-RSA-2（belief propagation-revised simulated annealing algorithm-2）［24］、禁忌搜索TS（Tabu search）［25］、TS-SA（Tabu search-simulated annealing algorithm）［25］都為啟發式隨機搜索算法。而回溯BT（backtracking algorithm）［26］、基于度啟發式的HBT（heuristic backtracking algorithm）［26］、動態度的ddeg-MAC（dynamic degree-maintaining arc consistency）［27］都為基于回溯的完備性求解算法，基礎的BT與TS算法在高維難解

實例中并不具有求解能力。從圖9（a）可以看到，當變量取80時，WSCH與MDSCH在同組算法中，p為0.12～0.14時展現的高概率求解，均優于對比算法，在p=0.14時，表現最好的MDSCH與對比算法中最優的BP-RSA-2相比，求解概率高出32%。而在p>0.14時，由于實例的復雜度增加，各算法均不能高效求解。如圖9（b），當變量n取100，在p=0.14時，實例的復雜度上升，MDSCH算法稍弱于BP-RSA-2、HBT。在p=0.13時，WSCH求解概率僅次于MDSCH，而MDSCH與對比算法中最優的TS-SA相比，求解概率高出16%。在變量n取100時，MDSCH算法在p=0.12時以概率1求解，為所有對比算法中最佳值。而無論變量n取80、100，在p取0.11、0.12時，兩種算法的求解效率均表現最佳。綜上分析，WSCH與MDSCH算法在高維難解實例中，對比各類啟發式算法表現出了高效的求解性能。

表3為RSA、GSA、WSCH和MDSCH四種算法在隨機的RB模型實例上，在各變量維度中分別運行10次，取約束密度0.16～0.20在接近可滿足性相變的實驗結果。ANVC表示平均不可滿足約束數，time為平均運行時間。在平均運行時間方面，對于復雜且難解的RB模型實例，WSCH和MDSCH算法的運行時間基本相當，相比之下，RSA和GSA算法的平均運行時間至少增加了近30%。在不可滿足約束數量方面，當變量維度較低（如n 取20或40）時，WSCH表現最佳。但在高維實例中，尤其是在變量維度較高（如n取60、80或100）且實例較復雜的情況下，MDSCH表現出色。值得注意的是，在復雜但可解的區域中，當約束密度為0.16時，MDSCH的平均不可滿足約束數量提高的效率最多。綜上所述，這些實驗結果表明，MDSCH在高維度和復雜RB模型實例上的性能表現優越，特別是在可滿足性相變點附近的情況下，其平均不可滿足約束數量顯著減少。

4 結束語

對大值域CSP的求解探索是極其有意義的，如在一些實際應用中，CSP的問題參數如域大小、變量數量、約束數量等可能不確定，RB模型可以用于生成多個實例，以測試不同參數下算法的表現。通過分析在不同參數配置下算法的性能表現，為實際應用中的問題選擇最佳參數設置以提高問題求解的效率和準確性。其次在自動化調度和資源分配問題中，RB模型可用于生成不同場景下的調度問題，這有助于評估自動化調度算法在處理多種不同場景下的性能。通過對多個場景下的調度問題進行建模和求解，可以優化資源分配，提高效率，最大程度減少成本。 本文提出了基于權重指導搜索的W-MCH和最小化值域MDMCH的兩種局部搜索方式，顯著提高了MCH算法在整體規模接近可滿足相變區域的求解效率。此外，融入退火策略的WSCH和MDSCH算法進一步增強了算法的局部搜索能力。這些算法在求解RB模型生成的CSP問題實例方面表現出色，尤其在高約束密度和復雜性下具有明顯的優勢。然而，這些算法仍有待優化。例如，對于高維實例，可以進一步優化權重處理，采用自適應權重調整策略，在迭代一定次數后重新映射各個變量的權重，實現更精確的搜索引導。未來的研究可以繼續探索這些算法在其他領域的應用，并優化它們以提高求解效率。

參考文獻：

［1］Frayman F，Mittal S. COSSACK： a constraint-based expert system for configuration tasks［M］//Knowledge-Based Expert Systems in Engineering： Planning and Design.Berlin：Springer，1987： 143-166.

［2］De Kleer J，Sussman G J. Propagation of constraints applied to circuit synthesis［J］. International Journal of Circuit Theory and Applications，1980，8（2）： 127-144.

［3］Nadel B A，Lin J. Automobile transmission design as a constraint satisfaction problem： modelling the kinematic level［J］. AI EDAM，1991，5（3）： 137-171.

［4］Mackworth A K. On seeing things，again［C］//Proc of IJCAI. 1983： 1187-1191.

［5］Achlioptas D，Kirousis L M，Kranakis E，et al. Random constraint satisfaction： a more accurate picture［C］//Proc of International Conference on Principles and Practice of Constraint Programming. Berlin： Springer，1997： 107-120.

［6］Molloy M. Models and thresholds for random constraint satisfaction problems［C］//Proc of the 34th Annual ACM Symposium on Theory of Computing. New York：ACM Press，2002： 209-217.

［7］Xu Ke，Li Wei. Exact phase transitions in random constraint satisfaction problems［J］. Journal of Artificial Intelligence Research，2000，12： 93-103.

［8］Fan Yun，Shen Jing. On the phase transitions of random k-constraint satisfaction problems［J］. Artificial Intelligence，2011，175（3-4）： 914-927.

［9］Fan Yun，Shen Jing，Xu Ke. A general model and thresholds for random constraint satisfaction problems［J］. Artificial Intelligence，2012，193： 1-17.

［10］趙春艷，范如夢，劉雅楠. 不同緊度下約束滿足問題的相變現象 ［J］. 計算機應用研究，2020，37（9）： 2739-2743. （Zhao Chunyan，Fan Rumeng，Liu Yanan. Phase transitions in random constraint satisfaction problem with various constraint tightness ［J］. Application Research of Computers，2020，37（9）： 2739-2743.）

［11］Huang Ping，Yin Ming Hao. An upper （lower） bound for Max （Min） CSP［J］. Science China Information Sciences，2014，57（7）：1-9.

［12］Xu Wei，Zhang Pan，Liu Tian，et al. The solution space structure of random constraint satisfaction problems with growing domains［J］. Journal of Statistical Mechanics： Theory and Experiment，2015，2015（12）： P12006.

［13］Zhou Guangyan. Hiding solutions in model RB： forced instances are almost as hard as unforced ones［EB/OL］. （2021-3-15）. https：//arxiv.org/abs/2103.06649.

［14］Xu Wei，Zhang Zhe. The solution space structure of planted constraint satisfaction problems with growing domains［J］. Journal of Statistical Mechanics： Theory and Experiment，2022，2022（3）： 033401.

［15］Cai Shaowei，Su Kaile，Chen Qingliang． EWLS： a new local search for minimum vertex cover［C］//Proc of the 24th AAAI Conference on Artificial Intelligence． Menlo Park： AAAI Press，2010： 45-50

［16］王曉峰，許道云. RB模型實例集上置信傳播算法的收斂性 ［J］. 軟件學報，2016，27（11）： 2712-2724. （Wang Xiaofeng，Xu Daoyun. Convergence of the belief propagation algorithm for RB model instances ［J］. Journal of Software，2016，27（11）： 2712-2724.）

［17］Xu Wei，Gong Fuzhou. Performances of pure random walk algorithms on constraint satisfaction problems with growing domains［J］. Journal of Combinatorial Optimization，2016，32（1）： 51-66.

［18］原志強，趙春艷. 兩種改進的模擬退火算法求解大值域約束滿足問題 ［J］. 計算機應用研究，2017，34（12）： 3611-3616. （Yuan Zhiqiang，Zhao Chunyan. Two improved simulated annealing algorithms for solving constraint satisfaction problems with large domains ［J］. Application Research of Computers，2017，34（12）： 3611-3616.）

［19］Bouhouch A，Bennis H，Loqman C，et al. Neural network and local search to solve binary CSP［J］. Indonesian Journal of Electrical Engineering and Computer Science，2018，10（3）： 1319-1330.

［20］Tnshoff J，Kisin B，Lindner J，et al. One model，any CSP： graph neural networks as fast global search heuristics for constraint satisfaction［EB/OL］. （2022-08-22）. https：//arxiv.org/abs/2208.10227.

［21］Korani W，Mouhoub M. Discrete mother tree optimization and swarm intelligence for constraint satisfaction problems［C］//Proc of ICAART. 2022： 234-241.

［22］Hossain M S. Constraint propagation and variable ordering heuristics for solving Constrained Partial CP-nets［D］. ［S.l.］：University of Regina，2023.

［23］Xu Ke，Boussemart F，Hemery F，et al. Random constraint satisfaction： easy generation of hard （satisfiable） instances［J］. Artificial Intelligence，2007，171（8-9）： 514-534.

［24］吳撥榮，趙春艷，原志強. 置信傳播和模擬退火相結合求解約束滿足問題 ［J］. 計算機應用研究，2019，36（5）： 1297-1301. （Wu Borong，Zhao Chunyan，Yuan Zhiqiang. Combining belief propagation and simulated annealing to solve random satisfaction problems ［J］. Application Research of Computers，2019，36（5）： 1297-1301.）

［25］李飛龍，趙春艷，范如夢. 基于禁忌搜索算法求解隨機約束滿足問題 ［J］. 計算機應用，2019，39（12）： 3584-3589. （Li Feilong，Zhao Chunyan，Fan Rumeng. Solving random constraint satisfaction problems based on tabu search algorithm ［J］. Journal of Computer Applications，2019，39（12）： 3584-3589.）

［26］范如夢，趙春艷，李飛龍. 啟發式回溯算法求解約束滿足問題 ［J］. 計算機應用研究，2021，38（5）： 1438-1442. （Fan Rumeng，Zhao Chunyan，Li Feilong. Heuristic backtracking algorithm to solve constraint satisfaction problems ［J］. Applied Research of Compu-ters，2021，38（5）： 1438-1442.）

［27］張學才，趙春艷. 基于動態度的回溯算法求解大值域約束滿足問題 ［J］. 計算機應用研究，2022，39（5）： 1427-1431. （Zhang Xuecai，Zhao Chunyan. Dynamic degree based backtracking algorithm to solve constraint satisfaction problems with large domains ［J］. Application Research of Computers，2022，39（5）： 1427-1431.）