基于圖嵌入和多標簽傳播的重疊社區檢測算法

高兵 宋敏 鄒啟杰 秦靜

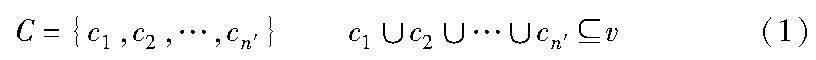
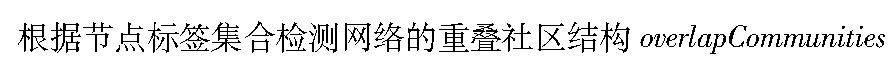
摘 要：為進一步優化重疊社區檢測算法，提出了一種新的基于度和節點聚類系數的節點重要性定義，按照節點重要性降序更新節點，固定節點更新策略，提高社區檢測的穩定性。在此基礎上，提出了一種基于圖嵌入和多標簽傳播的重疊社區檢測算法（overlapping community detection based on graph embedding and multi-label propagation algorithm，OCD-GEMPA）。該算法結合node2vec模型對節點進行低維向量表示，構建節點之間的權重值矩陣，根據權重值計算標簽歸屬系數，據此選擇標簽，避免了隨機選擇問題。在真實數據集和人工合成數據集上對該算法進行實驗驗證。實驗結果表明，與其他重疊社區檢測算法相比，OCD-GEMPA在EQ和NMI這兩個指標都有明顯提升，具有更好的準確性和穩定性。

關鍵詞：多標簽傳播；圖嵌入；重疊社區檢測；節點重要性；節點更新策略

中圖分類號：TP391?? 文獻標志碼：A??? 文章編號：1001-3695（2024）05-021-1428-06

doi： 10.19734/j.issn.1001-3695.2023.09.0423

Overlapping community detection based on graph embedding and multi-label propagation algorithm

Abstract：In order to further optimize the overlapping community detection algorithm， this paper proposed a new definition of node importance based on degree and node clustering coefficient， and the nodes were updated in descending order of node importance， and the node update strategy was fixed to improve the stability of community detection. On this basis， this paper proposed an OCD-GEMPA. The algorithm combined the node2vec model to represent the nodes in a low-dimensional vector， constructed a matrix of weight values between nodes， calculated the label attribution coefficient according to the weight values， and selected labels accordingly， avoiding the problem of random selection. Experimental verification of the algorithm on real data sets and synthetic data sets shows that compared to other overlapping community detection algorithms， the OCD-GEMPA algorithm has significant improvements in both EQ and NMI indicators， with better accuracy and stability.

Key words：multi-label propagation; graph embedding; overlapping community detection; node importance; node update strategy

0 引言

現實生活中，各類網絡隨處可見，例如社交網絡、道路交通網絡、文獻引用網絡，以及生物蛋白質網絡［1］等。這些大規模的復雜網絡有著巨大的潛在價值信息。社區結構［2］作為復雜網絡的重要特征，通常表現為社區內部節點聚集，社區間節點分散的特點。然而在真實世界中，社區結構呈現出一定的重疊性，即某些節點可能同時屬于多個社區。挖掘重疊社區結構對于理解網絡中的多重歸屬性、揭示隱藏的關系、精細化社區劃分以及實現個性化推薦和定制服務具有重要的意義。

近年來，重疊社區檢測［3］的研究已經取得了重大進展，涌現了各種算法。其中具有代表性的算法包括基于局部擴展優化的算法［4］、基于派系過濾的算法［5］和基于鏈接劃分的算法［6］等。上述算法對于挖掘網絡社區結構有一定效果，但其運算優化能力較弱，針對大規模網絡的社區劃分問題較為乏力。相比之下，標簽傳播算法的思想簡單易于實現，無須優化預定義的目標函數和社區的先驗信息就能夠以接近線性的時間復雜度挖掘出復雜網絡中的社區結構。Gregory［7］提出的COPRA就是標簽傳播算法中的典型代表。COPRA是標簽傳播算法LPA［8］的擴展版，其最大的優勢在于采用多標簽策略從而可以挖掘網絡中的重疊社區結構，但仍未解決標簽傳播算法的節點執行順序所帶來的不穩定性問題。在執行COPRA算法時，每次的社區劃分結果相差較大，劃分質量高低不均，算法的穩定性較差。另外，基于COPRA執行過程的分析可知，因為COPRA無差別對待節點，所以標簽傳播過程中存在標簽隨機選擇的問題，從而使得算法準確度不高。

針對COPRA存在的不足，很多學者對其做了改進。Lu等人［9］提出了一種改進的重疊社區檢測算法LPANNI，引入了鄰居節點影響指標NMI，在更新節點標簽時計算不同鄰居節點的NMI值，以更好地衡量不同節點的重要程度，解決了無差別對待節點的問題。將NMI值作為標簽選擇的依據，極大地避免了節點標簽的隨機選擇。為了進一步提高社區發現的準確率，劉繼等人［10］提出了一種基于圈結構的LPANNI優化算法，該算法采用了一種新的指標（圈比）來衡量節點重要性，并按照節點重要性固定節點序列，進一步增加標簽傳播過程的穩定性。但是以上兩種改進算法在計算鄰居節點影響力的時候僅考慮了節點的局部拓撲結構，忽略了不相鄰的節點之間也存在著一定的關聯。

為了更好地利用網絡的全局拓撲結構，已有許多學者將圖嵌入［11］應用到復雜網絡社區發現問題上，其中最常見的就是圖嵌入與傳統聚類算法的融合。Yang等人［12］提出了一種基于節點相似性和網絡嵌入的復雜網絡社區發現算法。該算法結合node2vec［13］獲取節點間的相似性值，并據此建立偏好網絡，完成初始社劃分。然后按照度量指標篩選出中心節點，利用K-means完成最終的社區劃分。Hu等人［14］提出了一種結合node2vec和譜聚類的社區發現算法。該算法首先利用node2vec獲取節點的嵌入向量，然后利用這些向量構建譜聚類算法的相似性矩陣，以對數據點進行聚類操作，從而得到社區劃分的結果。圖嵌入可以更好地利用網絡中的全局結構信息，為下游任務提供良好的基礎，但是傳統聚類只能用于非重疊社區結構的檢測。因此，需要進一步研究和開發適用于重疊社區檢測的圖嵌入社區發現算法。

目前，研究人員提出了許多基于節點相似性和節點重要性的社區檢測算法，旨在能夠進一步提高算法的準確性和穩定性。文獻［9］提出標簽傳播算法引入了節點重要性NI和基于Jaccard改進的相似性度量sim。但是，該算法在相似性度量上需要使用路徑長度閾值α以控制計算復雜度，且sim并未充分利用網絡中的全局拓撲結構信息。文獻［12］將圖嵌入引入到社區檢測領域，提出了無參數社區劃分算法，解決了文獻［9］超參數設置問題，同時也提高了節點相似性的準確度。但是，圖嵌入與傳統聚類的結合卻不能挖掘出更復雜的重疊社區結構。

綜上所述，基于標簽傳播的改進算法并沒有兼顧穩定性和全局拓撲結構的綜合考量。本文提出的基于圖嵌入模型的標簽傳播改進算法，結合了改進的節點重要性排序方法以及更高階的相似性度量，以進一步提高社區劃分的準確性和穩定性。

本文貢獻主要包括以下幾個方面：

a）提出了一種新的節點重要性定義，通過綜合考慮節點度和鄰居節點間關聯程度這兩個因素，可以更全面地評估節點的重要性；

b）設計了一種帶權重的社區歸屬系數公式，相對于傳統的隨機選擇方法，降低節點標簽的隨機選擇性，從而更準確地捕捉節點的歸屬關系；

c）提出了一種基于圖嵌入和多標簽選擇的重疊社區檢測算法OCD-GEMPA，與傳統重疊社區檢測算法相比，算法的準確度得到了顯著提升。

1 基本概念

G=（V，E）表示無向無權圖，其中V={v1，v2，…，vn}表示圖的頂點集合，E={e1，e2，…，en}表示圖的邊集合，n和m分別表示圖中節點和邊的數量。

定義1 重疊社區。網絡中的重疊社區集合C定義為

其中：n′表示重疊社區數量；C中的元素表示為一個重疊社區，重疊社區之間可能包含多個相同的節點。

定義2 圖嵌入。圖嵌入是一種將圖形數據映射到低維向量空間的技術，能夠將復雜的圖結構轉換為連續的向量表示，從而便于進行機器學習和數據分析任務。具體過程如圖1所示。

2 OCD-GEMPA算法的設計與實現

本文提出了基于圖嵌入和多標簽傳播的重疊社區檢測算法（overlapping community detection based on graph embedding and multi-label propagation algorithm，OCD-GEMPA），如圖2所示，該算法的核心部分主要包括節點更新順序和標簽更新策略兩個方面。下面從這兩個方面闡述算法的思想以及具體的實現過程。

2.1 節點更新順序

目前存在的一些多標簽傳播算法在初始化階段平等看待每個節點，并按照隨機順序對節點進行更新，這使得算法極具不穩定性。對節點進行重要性評估，并將其作為節點更新的依據，能夠極大地降低標簽傳播過程中所發生的不確定性。在OCD-GEMPA中，根據節點重要性值的大小對節點更新序列進行降序排列。節點重要性越大，節點成為潛在社區中心的可能性越大。重要性大的節點先更新在一定程度上能夠加快算法的收斂速度。

針對于節點的重要性評估問題，目前存在著許多衡量方法。其中，最為常用的方法主要包括度中心性、k-shell算法以及PageRank算法等。但是以上算法在評估節點重要性時，僅考慮節點本身的重要程度，卻忽略了其鄰居節點之間的緊密程度。節點本身的連接數量固為重要，但是鄰居節點之間的鏈接緊密度不容忽視，因為它衡量了整體的鏈接關系，能夠更加準確地評估一個節點的重要程度。

基于以上分析，在描述節點重要性方面，綜合考慮了節點的度和局部聚類系數，提出了一種新的基于度和節點聚類系數的節點重要性定義，不但考慮了節點本身的連接數，還考慮了節點的鄰居之間的連接緊密度。節點i的重要性NI（i）定義為

其中：ki表示與節點i存在鏈接關系的節點數量；CC（i）表示節點i的局部聚類系數；Ri表示與節點i存在鏈接關系的鄰居節點之間的鏈接數量（可借助經過i的三角形數得到）。

以圖3的無向無權圖為例，計算節點3的重要性NI（3）的值。其中k3=3，R3=5（虛線部分表示通過節點3的三角形個數）， CC（3）=1.67，那么NI（3）=3×（1+1.67）=8.01，同理，節點5的NI值為4×（1+0.1.33）=9.32，通過計算可知節點5的重要性大于節點3。

2.2 標簽更新策略

根據文獻［8］提出的多標簽傳播策略，算法能夠檢測到網絡中的重疊社區結構，其中每個節點可以擁有多個社區標簽，即節點可被劃分到多個社區。然而在算法中，當節點接收到來自鄰居節點的標簽并去除掉無效標簽的時候，會存在以下兩種隨機選擇的情況：

a）當待選擇的鄰居節點標簽具有同樣的歸屬系數值時，節點就會隨機選擇其中一個；

b）如果所有標簽的歸屬系數都小于閾值也會隨機選擇其中一個。

為了盡可能避免這種隨機選擇的情況，算法采用圖嵌入模型node2vec對節點進行低維向量表示，然后構建節點間相似性矩陣，并將其作為歸屬系數權重，使得節點更偏重選擇跟它最具相似性的節點標簽。

目前存在許多關于節點相似性的計算方法，比如Jaccard相似性、Dice相似度、katz指標等，但是它們都有一定的局限性。例如，Jaccard沒有充分利用網絡拓撲結構信息，僅考慮節點一階鄰居共同數量，Katz指標權重衰減因子的最優值只能通過大量的實驗驗證獲得等。

圖嵌入是一種深度學習方法，它將復雜的圖數據映射為低維稠密的向量，相較于其他相似性度量，向量空間有更豐富的方法工具集。目前，基于圖嵌入的標簽傳播算法較少，大都是基于圖嵌入做傳統聚類（K-means）的非重疊社區發現算法，將圖嵌入結合到標簽傳播算法中，不僅能夠極大程度地保留網絡的拓撲結構信息，獲取更高階的相似性度量，提高算法的準確度，同時還能夠檢測出網絡中的重疊社區結構，更加符合真實的結構劃分。

在OCD-GEMPA算法中使用node2vec模型進行網絡表示學習。不同于基于DFS鄰域的DeepWalk［15］和基于BFS鄰域的LINE［16］，node2vec是一種綜合考慮DFS鄰域和BFS鄰域的圖嵌入方法，可以看作是DeepWalk的一種擴展。它采用了有偏的隨機游走算法并結合 skip-gram 算法學習圖嵌入，通過參數設置來控制搜索策略，從而有效地平衡了 embedding 的同質性和結構有效性。 相比于DeepWalk，node2vec優化了采樣方式與序列生成方式，提高效率的同時也提升了效果。

以圖4（a）為例，采用node2vec模型學習網絡拓撲結構，獲取節點的低維向量表示。通過對節點做embedding，節點之間的相似度就轉換成了向量之間的相似度。采用余弦相似度去衡量兩個向量之間的相似性，即為兩個向量的點積除以兩個向量大小的乘積，具體公式如下：

其中：A、B表示兩個向量，Ai表示向量A的第i個元素。

基于以上方法獲得圖2的節點相似性矩陣W如式（5）所示，其中行列表示節點ID。

為了避免標簽過多從而造成傳播過程的復雜性，本文算法采用主導標簽策略，只傳播社區歸屬系數最大的主導標簽，為保證主導標簽的唯一性，當出現多個時隨機選擇一個，節點u的主導標簽具體表示如下：

當節點u更新其標簽時，它從其鄰居節點接收多個主標簽，并形成標簽集如下所示。

LND={l（Dl1，b1），l（Dl2，b2），…，l（Dlv，bv）}（7）

其中：v∈N（u），N（u）表示節點u的鄰居節點集合；bv表示節點v對社區Dlv的社區歸屬系數。

構建的節點相似性矩陣作為社區歸屬系數的權重值。從上述構建的矩陣可以看出，節點間的相似值均不相同，從而極大地避免歸屬系數相同而導致的節點隨機選擇標簽的現象，其中帶權重的新歸屬系數計算如下：

2.3 算法設計

2.3.1 算法步驟描述

首先，根據本文提出的基于度和節點聚類系數的節點重要性定義，計算所有節點的節點重要性值，并將它們降序排列，以確定節點更新的順序；然后，初始化節點的標簽，將其默認設置為主導標簽；接下來，使用帶權重的社區歸屬系數來更新節點的標簽，將具有較大歸屬系數的標簽設置為節點的主導標簽；選擇相鄰節點的主導標簽，并過濾掉具有較小社區歸屬系數的無效標簽，從而形成節點的主導標簽集合；最后，當節點的主導標簽集合不再發生變化或達到最大迭代次數T時，算法停止，從而得到最終的重疊社區結構。

算法1 OCD-GEMPA

2.3.2 節點更新與標簽傳播示例

圖4介紹了OCD-GEMPA算法的節點更新和標簽傳播過程，對節點NI值進行降序排序從而獲得的節點更新順序為1→5→9→2→4→6→8→3→7。

以圖4（a）為給定的簡單無向無權圖為例，首先，初始化節點標簽為每個節點對應的ID并將所有節點的歸屬系數設置為1，如圖4（b）所示。按照節點更新順序進行節點標簽傳播，以節點1為例，其相鄰節點2，4，5，6，8，9的標簽為（2，1）（4，1）（5，1）（6，1）（8，1）（9，1），然后根據給定的帶權重的歸屬計算公式計算出標簽的新歸屬系數值，從而得到新的節點標簽集合{（2，0.160），（4，0.165），（5，0.178），（6，0.169）， （8，0.167），（9，0.170）}，按照標簽長度的倒數去掉無效標簽，即去掉（2，0.160）（4，0.165）這兩個標簽，最后對剩下的標簽進行標準化處理從而得到節點1最終的標簽集合為{（5，0.249），（6，0.251），（8，0.247），（9，0.253）}，主導標簽為（9，0.253），其余節點標簽傳播過程與節點1相同，得到的最終節點標簽集結果如圖4（c）所示。經過兩次迭代，每個節點的標簽集合不再發生變化，算法結束，整個網絡劃分成兩個社區，其中節點1為重疊節點，劃分結果如圖4（d）所示。

2.4 時間復雜度分析

假設n代表網絡中節點的個數，m代表邊的個數，k代表網絡節點的平均度數，T代表最大迭代次數。在固定節點更新順序階段，節點重要性計算的時間復雜度是O（kn+nk2），節點重要性排序采用基數排序算法，時間復雜度是O（n），那么在固定節點更新順序階段的總時間復雜度為O（kn+nk2）。在標簽傳播階段，生成節點相似性矩陣的時間復雜度是O（n2），標簽傳播的時間復雜度取決于算法的迭代次數，對于第一次迭代，它的時間復雜度是O（kn），則第一次迭代的總時間復雜度為O（n2+kn），那么標簽傳播階段的總時間復雜度是O（T（kn+n2）。

3 實驗分析

本文使用了7個不同規模的真實數據集和4個人工合成數據集對OCD-GEMPA算法進行了實驗。所有實驗都在一臺搭載3.20 GHz的AMD Ryzen 7 5800H處理器和16 GB內存的筆記本電腦上進行。實驗代碼均采用Python 3.8編寫。

3.1 真實數據集和人工數據集

3.1.1 真實數據集

表1詳細列出了實驗所需的7個真實網絡數據集，n表示網絡的節點個數，m表示網絡中邊的數量，k表示網絡中的平均度數。

3.1.2 人工數據集

LFR benchmark基準程序是近年來較為廣泛使用的人工基準網絡程序，因為其生成的網絡可以很好地表示出節點度和社區規模分布的異質性，通過調節參數來生成不同網絡，主要參數說明如表2所示。

本實驗使用LFR基準程序生成了四組網絡，為了更好地驗證算法的準確性，每一組都會設置一個可變參數，以LFR1為例，u設置為0.1～0.5，其他參數保持不變，詳細的參數設置如表3所示。

3.2 對比算法介紹及參數設置

為了能夠更好地驗證OCD-GEMPA的性能，將其與DEMON［17］、LFM_EX［18］、SLPA［19］、COPRA四種重疊社區檢測基線算法進行對比實驗，下面是算法介紹以及參數設置。

a）LFM_EX：一種基于適應度函數和社區相似性的改進LFM算法，解決了LFM算法由于其回溯步驟所產生的不歸屬任何一個社區的離散節點問題。

b）DEMON：一種以局部優先的方法發現分層和重疊社區的算法。

c）SLPA：基于說話人-聽眾規則的標簽傳播重疊社區檢測算法。

d）COPRA：基于標簽傳播的重疊社區檢測算法，RAK的改進算法。

本文對比算法的參數設置如下：COPRA算法中v的范圍為3～8;對于SLPA算法，在合成網絡中，標記概率閾值r從0.01～0.1變化，間隔為0.01，而在真實網絡中，r從0.05～0.5變化。

3.3 評價指標

3.3.1 模塊度EQ

模塊度EQ［20］用于評價社區劃分結果的優劣。模塊度值越接近1，則表示社區劃分的質量越高；反之模塊度越小，表明社區劃分結果較差。模塊度的定義如下：

其中：m為網絡中邊的總數；c為劃分得到的社區的數目；Oi為節點i所屬的社區個數；ki為節點i的度；Aij用于判斷節點i和j之間是否存在連接，若存在連接則Aij為1，否則為０。

3.3.2 標準化互信息NMI

標準化互信息（normalized mutual information，NMI）［21］是用于測量兩種數據分布之間吻合程度的一種方法，可以作為網絡社區劃分結果的評價指標。其公式如下：

其中：CA為標準社區劃分的結果；CB為算法所得到社區劃分的結果；矩陣Ｎ的行對應標準社區結果，列對應算法得到的社區檢測結果；Ni.為第i行的總和；N.j為第j列的總和。NMI值越大，說明算法劃分社區的效果越好。

3.4 真實數據集上的實驗結果

3.4.1 EQ

圖5為OCD-GEMPA與其他四種基線算法在7個真實數據集上的實驗結果。從圖中可以看出，OCD-GEMPA除在netscience數據集上EQ值略低于SLPA之外，在其他真實數據集上的EQ值均高于另外四種基線算法。另外，與SLPA和COPRA這兩種多標簽傳播算法相比較，OCD-GEMPA總體上表現更好，這說明引入圖嵌入模型計算節點相似度矩陣作為歸屬系數的權重值能夠更好地指導標簽選擇，在一定程度上提高了算法的準確度。

3.4.2 穩定性分析

為了驗證算法的穩定性，將OCD-GEMPA算法與COPRA、SLPA這兩個經典的標簽傳播算法在六個真實數據集上進行20次模塊度方差值的實驗。表4列出了穩定性實驗的結果，可以看出，節點之間的權重極大地降低了標簽隨機選擇的可能性，算法的穩定性更好。

3.5 人工合成網絡上的實驗結果

3.5.1 混合參數mu變化對算法的影響

圖6給出了隨著混合參數mu的不斷增加，各算法在LFR1網絡上的EQ值和NMI值變化。mu值不斷增加，社區相互混合，網絡結構就會越復雜。以COPAR為例，在mu從0.3增加到0.4這個過程中，EQ和NMI兩值的下降幅度最大。這是因為在社區結構相互混合的情況下，每個社區都受到鄰居社區噪聲的影響，那么在標簽傳播過程中鄰居節點的選擇就是關鍵，COPRA隨機選擇鄰居節點，而OCD-GEMPA是根據節點權重值選擇，所以從整體上看，OCD-GEMPA的下降趨勢較小，整體性能相對較好。

3.5.2 重疊節點參數on變化對算法的影響

圖7展示的是在重疊節點參數on的不斷增加的情況下，各算法在LFR2上的EQ值和NMI值變化。重疊節點的增加也就意味著社區之間的重合越多，網絡結構越復雜。由圖7（a）知，on與EQ值呈負相關。從整體上看，OCD-GEMPA無論是EQ還是NMI值均優于其他算法，變化幅度最小。這是因為圖嵌入學習網絡拓撲，通過考慮高階臨近度獲取節點之間更好的相似性，即便網絡結構復雜，依舊可以選擇當下最相似的鄰居節點，為標簽傳播奠定良好的基礎。

3.5.3 重疊節點的社團隸屬數om變化對算法的影響

如圖8（a）所示，隨著om值的增加，各算法在LFR3數據集上的EQ值呈現下降趨勢。COPRA整體波動較大，這是因為算法在執行過程中存在鄰居節點隨機選擇的問題，使得準確度較低，穩定性較差。OCD-GEMPA采用節點相似性矩陣作為標簽歸屬系數的權重極大地避免了鄰居隨機選擇，在準確度和穩定度上都有了很大提高。整體表現優于其他四類基線算法。

3.5.4 節點數量n變化對算法的影響

圖9展示的是隨著網絡規模的不斷擴大，各算法在LFR4數據集上的具體表現。很明顯，COPRA、SLPA和OCD-GEMPA整體波動性較小且EQ值和NMI值較高，說明標簽傳播算法在大規模網絡重疊社區發現問題上也具有良好的性能。而局部擴展優化算法LFM_EX的EQ值和NMI值呈現下降趨勢，這說明該算法不適合大規模網絡的社區檢測。從整體看，OCD-GEMPA在網絡節點n不斷增加的情況下依然能夠很好地檢測重疊社區，主要原因是固定的節點更新順序和節點依據權重值選擇鄰居標簽這兩方面使算法的準確度和穩定性都得到了很大的提高。

表5列出了節點數量由1 000～10 000組成的不同人工網絡上各算法劃分的重疊社區數量對比情況，true表示真實劃分結果。從表5可以清楚地看出，隨著網絡規模的不斷擴大，OCD-GEMPA仍能夠正確地劃分社區。

4 結束語

本文提出了一種基于圖嵌入和多標簽傳播的重疊社區檢測算法OCD-GEMPA。該算法采用固定節點更新策略，提出了一種新的度量節點重要性的衡量方法和帶權重的社區歸屬系數公式，極大地避免了節點隨機選擇，提高了算法的準確度。節點屬性對于節點的相似性度量也有著很重要的參考價值，下一步將繼續研究帶有節點屬性的重疊社區發現問題。

參考文獻：

［1］Li Meizi，Lu Shuyi，Zhang Lele，et al. A community detection method for social network based on community embedding ［J］. IEEE Trans on Computational Social Systems，2021，8（2）： 308-318.

［2］Acman M，Van Dorp L，Santini J M，et al. Large-scale network analysis captures biological features of bacterial plasmids ［J］. Nature Communications，2020，11（1）： 2452.

［3］Gao Yang，Yu Xiangzhan，Zhang Hongli. Overlapping community detection by constrained personalized PageRank ［J］. Expert Systems with Applications，2021，173： 114682.

［4］郭娜，鄭曉艷. 基于最大生成樹的重疊社區發現算法 ［J］. 計算機應用研究，2020，37（S2）： 170-172，180. （Guo Na，Zheng Xiao-yan. Overlapping community discovery algorithm based on maximum spanning tree ［J］. Application Research of Computers，2020，37（S2）： 170-172，180.）

［5］Gupta S K，Singh D P，Choudhary J. A review of clique-based overlapping community detection algorithms ［J］. Knowledge and Information Systems，2022，64（8）： 2023-2058.

［6］Gabardo A C，Berretta R，Moscato P. M-link： a link clustering memetic algorithm for overlapping community detection ［J］. Memetic Computing，2020，12： 87-99.

［7］Gregory S. Finding overlapping communities in networks by label pro-pagation ［J］. New Journal of Physics，2010，12（10）：103018.

［8］Li Chunying，Tang Yong，Tang Zhikang，et al. Motif-based embedding label propagation algorithm for community detection ［J］. International Journal of Intelligent Systems，2022，37（3）： 1880-1902.

［9］Lu Meilian，Zhang Zhenglin，Qu Zhihe，et al. LPANNI： overlapping community detection using label propagation in large-scale complex networks ［J］. IEEE Trans on Knowledge and Data Enginee-ring，2018，31（9）： 1736-1749.

［10］劉繼，賈芳弟. 基于圈結構的 LPANNI 優化算法 ［J］. 計算機應用研究，2022，39（9）：2717-2722，2744. （Liu Ji，Jia Fangdi. LPANNI optimization algorithm based on circle structure ［J］. Application Research of Computers，2022，39（9）：2717-2722，2744.）

［11］Wang Xiao，Bo Deyu，Shi Chuan，et al. A survey on heterogeneous graph embedding： methods，techniques，applications and sources ［EB/OL］. （2022）. https：//arxiv.org/abs/2011.14867.

［12］Yang Xuhua，Wang Lei，Ye Lei，et al. Complex network community detection algorithm based on node similarity and network embedding ［J］. Computer Science，2022，49（3）： 121-128.

［13］Grover A，Leskovec J. node2vec： scalable feature learning for networks ［C］// Proc of the 22nd ACM SIGKDD International Confe-rence on Knowledge Discovery and Data Mining.New York：ACM Press，2016： 855-864.

［14］Hu Fang，Liu Jia，Li Liuhuan，et al. Community detection in complex networks using node2vec with spectral clustering ［J］. Physica A： Statistical Mechanics and its Applications，2020，545： 123633.

［15］Berahmand K，Nasiri E，Rostami M，et al. A modified DeepWalk method for link prediction in attributed social network ［J］. Computing，2021，103： 2227-2249.

［16］Zhang Zhengyan，Yang Cheng，Liu Zhiyuan，et al. Cosine： compressive network embedding on large-scale information networks ［J］. IEEE Trans on Knowledge and Data Engineering，2020，34（8）： 3655-3668.

［17］Coscia M，Rossetti G，Giannotti F，et al. DEMON： a local-first disco-very method for overlapping communities ［C］// Proc of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York：ACM Press，2012： 615-623.

［18］Zhang Lingxiao，Yan Xuefeng. An improved LFM algorithm based on fitness function and community similarity ［C］//Proc of IEEE International Conference on Parallel & Distributed Processing with Applications，Big Data & Cloud Computing，Sustainable Computing & Communications，Social Computing & Networking. Piscataway，NJ：IEEE Press，2019： 9-15.

［19］Xie Jierui，Szymanski B K，Liu Xiaoming. SLPA： uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process ［C］// Proc of the 11th IEEE International Confe-rence on Data Mining Workshops. Piscataway，NJ：IEEE Press，2011： 344-349.

［20］Chattopadhyay S，Basu T，Das A K，et al. A similarity based genera-lized modularity measure towards effective community discovery in complex networks ［J］. Physica A： Statistical Mechanics and Its Applications，2019，527： 121338.

［21］Hesamipour S，Balafar M A. A new method for detecting communities and their centers using the Adamic/Adar Index and game theory ［J］. Physica A： Statistical Mechanics and Its Applications，2019，535： 122354.