一種基于離散時間一致性理論的多機器人分布式巡邏算法

張鵬超 李宗剛

摘 要：在多機器人巡邏任務中，由于通信距離的限制，單個機器人很難獲得全局信息。然而，現有的大多數多機器人分布式巡邏算法都要求每個機器人獲得其巡邏區域的全局信息進行決策。因此，考慮到通信半徑約束和局部信息約束，為了通過相鄰機器人之間的交互完成巡邏任務，基于離散時間一致性理論提出了兩種巡邏算法。算法1使用全局信息進行決策，算法2基于離散時間一致性理論實現局部信息對全局信息的預測進行決策。通過模擬器Stage對所提算法與對比算法在不同機器人數量、通信半徑、地圖環境下進行了對比。實驗驗證了所提出的基于局部信息的分布式多機器人巡邏算法具有與原算法類似的特性和性能，能夠使機器人在沒有全局信息的情況下判斷全局狀態，并基于鄰居之間的協商完成巡邏任務。

關鍵詞：巡邏；多機器人系統；分布式協同；離散時間一致性

中圖分類號：TP242?? 文獻標志碼：A??? 文章編號：1001-3695（2024）05-027-1470-10

doi： 10.19734/j.issn.1001-3695.2023.08.0421

Distributed patrol algorithm for multi-robot systems based on discrete-time consensus theory

Abstract：In the multi-robot patrol task， it is difficult for a single robot to obtain global information due to the limitation of the communication distance. However， most existing multi-robot distributed patrol algorithms require each robot to obtain global information of its patrol area for decision-making. Therefore， this paper addressed on the communication radius constrain and the local information constrain to completes patrol tasks through the interaction between neighbor robots， and proposed two solution algorithms based on discrete-time consensus theory. Algorithm 1 used global information for decision-making. Algorithm 2 used discrete-time consensus theory to predict and make decisions based on local information. Through the simulator Stage， the proposed algorithm and the comparison algorithm were simulated and compared under different robot numbers， communication radii and map environments. The simulation verifies that the proposed fully distributed multi-robot patrol algorithm based on local information has similar characteristics and performance to the original algorithm， enabling robots to judge the global state without global information and complete patrol tasks based on the negotiation between neighbors.

Key words：patrolling; autonomous multi-robot system; distributed coordination; discrete-time consensus theory

0 引言

多機器人巡邏問題（MRPP）是指多個機器人在目標區域內或周圍移動，以保護或監督目標區域，達到安全目的的活動［1］。多機器人巡邏應用廣泛，例如城市安保巡邏、邊境巡邏、海岸線巡邏、化工廠集群安保巡邏［2］、森林火災預防巡邏等。通常，巡邏可以分為常規巡邏和對抗巡邏兩類［1］，常規巡邏指的是通過頻繁到訪目標區域內部以掌握該區域，對抗巡邏旨在通過檢測入侵者來保護目標區域。

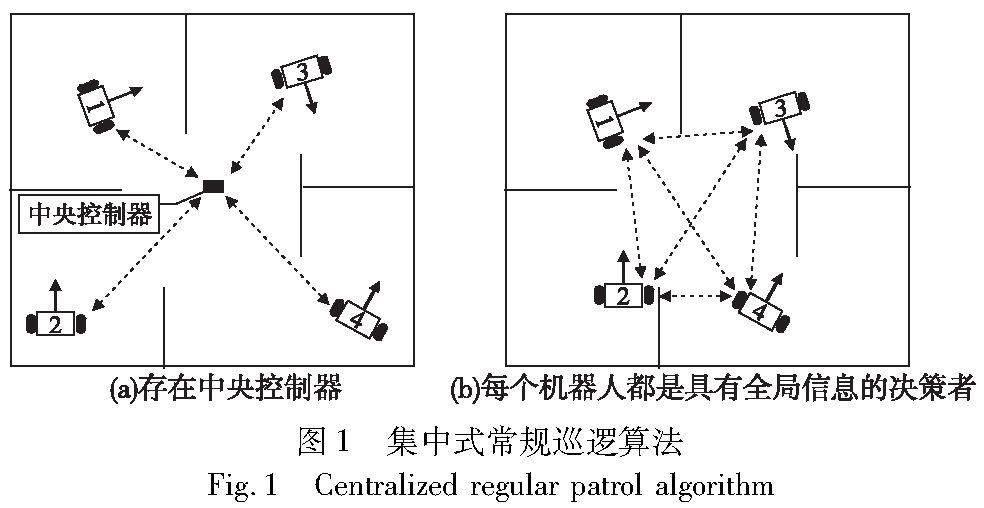
常規巡邏問題廣泛研究的算法有兩種類型：a）集中式算法。如圖1所示，其中要么存在一個中央控制器，要么每個機器人都可以獲得全局信息并獨立決策。集中式算法易于應用，適用于小規模巡邏任務。但是受中央控制器宕機和全局信息獲取的影響較大，因此魯棒性較差。b）分布式算法。如圖2所示，每個機器人收集周圍的環境信息并與鄰居進行交換，即每個機器人只使用局部信息來作出決策。分布式算法具有更好的可擴展性和容錯性，適用于大規模巡邏任務。出于本文的研究目的，僅將分布式算法的文獻總結如下。

現有的分布式多機器人巡邏算法主要包括反應式策略、基于學習的方法和基于拍賣的方法。反應式策略是指每個機器人選擇效用值最高的鄰居節點作為目標節點。因此，通常采用拓撲圖對環境進行建模。效用函數和評價標準可以通過空閑時間［3］、平均空閑時間［4，5］、全局平均最大空閑時間［6］、節點重要度［7］、期望空閑時間［8］、周圍鄰居的意圖［9］、不確定度［10］等因素來構建。評價指標采用空閑時間、不確定度等因素構造。但是，現有反應策略大都采用將到達和意圖信息發送給所有其他機器人的方式。因為每個機器人都需要拿到全局信息，所以不是完全的分布式策略。基于學習的方法通過積累歷史經驗幫助機器人適應動態環境。文獻［9，11］提出了GBS、SEBS和CBLS算法，以貝葉斯算法實現機器人的學習，并通過空閑時間對算法進行評估。全局信息（包括到達信息和意圖信息）通過無線自組織網絡（MANET）發布和傳輸。仿真分析了不同通信故障率對巡邏效果的影響。然而沒有考慮通信距離和機器人具體位置因素。基于長短期記憶網絡的RLPM是在集中式算法HPCC上訓練的，并在機器人之間沒有通信的情況下工作。雖然RLPM算法不需要全局信息就可以實現接近于被學習的原始算法的性能，但是需要對特定地圖和算法進行大量的訓練。在基于拍賣的方法中，每個節點都被視為一個要分配的任務。每個機器人獨立地求解其投標值并同所有其他機器人完成競標以判斷是否將競標節點加入任務清單［12，13］。DTAP和EDCP都要求每個機器人將投標值發送給所有其他機器人進行投標，以確定是否將投標節點添加到其任務列表中。因為競標過程中需要將出價信息發送到所有其他機器人，所以其集群大小和巡邏范圍受到了限制，算法不是完全的分布式巡邏算法。

綜上所述，現有文獻中的大多數分布式巡邏算法雖然實現了線上自主決策，但是大都需要所有其他機器人的信息來作出決策，也就是說巡邏問題是基于全局信息來解決的。隨著機器人規模的增加和巡邏范圍的擴大，機器人在有限的硬件資源下傳輸、獲取、存儲全局信息的難度隨之上升［14］。多機器人系統的通信要求、存儲要求和計算要求也隨著機器人數量的提高而提高，導致系統成本升高。因此有必要研究基于機器人自身局部信息的完全分布式的巡邏算法。例如對于有限通信范圍內考慮連通性保持因素的巡邏算法研究［15～17］。一致性算法使得機器人在沒有全局信息的情況下只需要相鄰機器人之間的協商，就能夠達成狀態信息的一致。一致性算法在分布式多機器人系統協同控制中的理論優勢使得設計基于局部信息的多機器人分布式巡邏算法成為可能。

基于以上分析，本文做了以下工作：

a）建立了機器人之間的關系拓撲描述；

b）提出了一種基于全局信息的巡邏算法；

c）提出了一種基于局部信息的完全分布式巡邏算法，使得機器人通過鄰居間通信協商、自身局部信息存儲、局部信息計算求解完成巡邏任務。

1 問題描述

考慮用多個移動機器人對給定環境進行巡邏，實現對環境狀態變化的實時監控。由于所考慮環境的結構特征已知，故采用無向圖G1（V1，E1）對環境進行建模。其中頂點集V1={v1，v2，…，vn}表示在環境中所選取的若干關鍵節點，邊集E1={eij}表示節點之間所存在的路徑，如圖3所示。頂點vi的相鄰點的集合稱為頂點vi的鄰居，記為NG1（vi），NG1（vi）={vq∈V1：ei，q∈E1}。從而所考慮巡邏問題可視為多機器人通過合作對頂點集的遍歷。

多機器人之間的關系也采用圖G2（V2，E2）表示，其中V2={r1，r2，…，rm}表示用于巡邏的機器人，E2={cij}表示機器人之間的關系。當cij=1時，機器人ri可以接收到機器人rj的信息，反之不能。機器人ri相鄰機器人的集合稱為機器人ri的鄰居，記為NG2（ri），NG2（ri）={rq∈V：ci，q∈E}。所有機器人在巡邏任務開始前已知拓撲地圖G1（V1，E1），并建立了初始關系G2（V2，E2）。

本文將機器人之間的關系G2（V2，E2）分為基于固定拓撲的關系和基于距離的關系兩種類型。前者通過固定機器人之間的關系實現固定的拓撲結構，后者預先設計機器人的通信半徑，通過機器人的移動實現關系變化。本文在分析中采用固定關系分析機器人關系對巡邏效果的影響，在實驗中考慮通信半徑實現的關系變化，每個機器人具有相同的通信半徑。

需要說明的是，多個機器人能否實現對環境的有效巡邏，取決于多機器人系統獲取、傳遞并利用環境信息的方式。現有文獻中，機器人到達目標節點后，向所有其他機器人廣播巡邏節點到達信息、目標巡邏節點信息等其他信息。每個機器人在進行決策時所使用信息均為巡邏環境所有節點的信息。也就是說，巡邏問題的解決是基于全局信息解決全局問題。考慮到單個機器人難以獲取全局信息的情況，有必要設計一種基于局部信息和鄰居間的通信的完全分布式巡邏算法。

利用一致性理論在局部信息估計全局信息的理論基礎，選取合適的狀態信息和一致性算法，能夠實現完全分布式巡邏算法。總的來說，一致性理論有以下三個好處：a）隨時都可以獲得最新的協商結果，而不需要判斷所獲取的全局信息是否完整；b）保密性和擴展性較好，因為協商信息是鄰居機器人之間相互協商的結果，而且是局部信息，受群體中單個機器人的影響小；c）能夠在巡邏算法中考慮通信半徑等實際因素，從而建立機器人之間的關系。因此，本文將一致性理論作為理論依據。

由于被協商的狀態量與時間無關，采用離散時間一致性理論建立協同算法。離散時間一致性理論的迭代公式為

其中：xki代表機器人i第k次協商的狀態信息和協商變量。通過設計不同的函數f實現不同的一致性。如果所有機器人的狀態最終趨于一致，則稱達成了離散時間一致性，如式（2）所示。

因此，本文研究了如何基于離散時間一致性理論實現鄰居機器人之間的協商行為。從而實現了一種基于局部信息和通信半徑約束的分布式巡邏算法。

所提算法的評價包括巡邏效果的評價以及一致性算法的協商效率兩個部分。通過空閑時間評價多機器人常規巡邏的巡邏效果。頂點vi在t時刻的瞬時空閑時間定義如式（3）所示。

Ivi（t）=t－tlast（3）

其中：tlast表示頂點最近一次被訪問的時刻。頂點vi在t時刻的平均空閑時間定義如式（4）所示。

此外，定義了全圖空閑時間標準差IGstddev、全圖空閑時間最大值IGmax。用干擾率Ifrate（每分鐘的干擾次數）評價兩個機器人距離過近產生的沖突。

多機器人系統離散時間一致性算法的協商效果通常用協商次數k評價。首先定義機器人ri第k次協商的收斂誤差εki如式（6）所示。

當收斂誤差εki在誤差限Δ以內時稱協商收斂，如下所示。對應的協商次數稱為收斂協商次數kconv。

|εki|<Δ（7）

結合巡邏算法和一致性算法，機器人可以通過局部信息來解決全局問題。本文感興趣的是通過鄰居機器人之間的通信來建立一個完全分布式的多機器人巡邏算法。問題陳述如下：

考慮使用多個機器人G2（V2，E2）對目標區域G1（V1，E1）進行巡邏。機器人關系G2由通信半徑約束R形成，每個機器人只能得到相鄰機器人的局部信息。目標是設計一種完全分布式巡邏算法，使機器人團隊以局部信息、局部決策和局部執行完成巡邏任務。

2 基于離散時間一致性理論的分布式巡邏算法

根據基于一致性算法的分布式多機器人協同控制設計思路，構建算法需要兩步：a）設計一個具有全局信息的集中式策略；b）基于一致性算法將全局信息轉換為局部信息，建立分布式算法［18］。

因此，本文從離散時間一致性算法的實現、集中式多機器人巡邏算法和分布式多機器人巡邏算法三個方面描述所建立的分布式巡邏算法。

2.1 離散時間一致性算法

2.1.1 離散時間一致性算法

根據最終收斂一致狀態值的不同，一致性可分為平均一致、最大一致、最小一致等［19］。

平均一致指的是收斂值為各個機器人初始值的平均值，采用文獻［20］提出的離散時間一致性算法，其形式如下：

其中：p［k］ij為第k次迭代的信息權重。式（8）可寫成矩陣形式，如式（9）所示。

其中：L［k］是拉普拉斯矩陣，它表示第k次協商時機器人之間的關系。當機器人之間的關系由無向圖表示時收斂條件有兩個［20～22］。首先，機器人之間的關系拓撲是連通的或聯合連通的。其次，ε∈（0，1/dmax），dmax=maxilii表示圖G2的最大出度。dmax也表示機器人的通信對象上限，即機器人的通信對象越多，系數ε越小，收斂越慢。

最大一致指的是收斂值為各個機器人初始值的最大值。離散時間一致性迭代形式如下：

x［k+1］i=max（a［k］i1×x［k］1，…，a［k］im×x［k］m） ?i=1，…，m（13）

x［k+1］i=max（A［k］×x［k］i） i=1，…，m（14）

其中：A［k］代表第k次協商時的鄰接矩陣。當機器人之間存在信息交換時aij=1，否則aij=0。經過多次協商，所有協商變量即可收斂到最大值。類似地，可以收斂到所有機器人初始狀態的最小值。

2.1.2 離散時間一致性算法實現

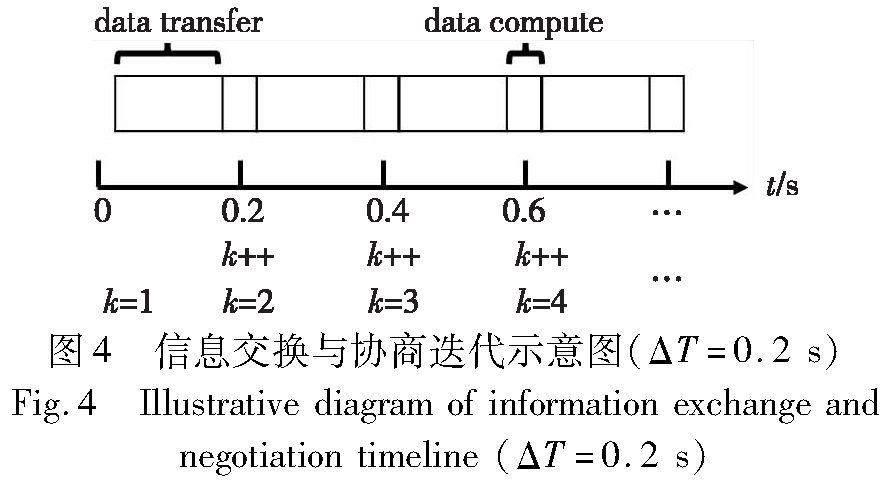
在現實過程中，巡邏機器人之間的關系與其空間位置密切相關，需要考慮其關系的變化。當兩個機器人很接近時，它們應該能夠直接建立關系。為了使機器人之間完成信息交換，給每一次迭代預留單位時間ΔT，定義為單位協商時間。單位協商時間的大小通常與多機器人系統的通信狀況和計算能力相關。此外，迭代計算時刻由獨立于機器人的壁鐘時間決定，通過網絡獲得、判斷和校正壁鐘時間。因此，將機器人迭代計算時刻序列定義為tk=k×ΔT（k=1，2，…）。

基于上述過程，只要機器人在單位協商時間ΔT內完成信息交換，那么就確認機器人在該次計算中存在信息傳輸。這也意味著表示機器人之間關系的拓撲G2（V2，E2）在不同的ΔT內可以不同。因此，上述迭代過程能夠適應機器人關系的變化。

2.1.3 重復進行的協商過程

因為節點被訪問，所以需要刷新收斂值以預測最新全局信息。循環協商即以ktotal為周期指定協商次數重復進行的協商。ktotal是所有機器人已知的。每個重復的協商都被稱為一個循環。當k=ktotal時，協商的狀態信息達成一致，從而用于估計全局信息并重新開始一輪新的協商。

協商算法收斂的協商次數稱為收斂協商次數kconv。為了確保拿到收斂值，收斂協商次數必須小于給定的協商次數，kconv

ttotal=ktotal×ΔT， tconv=kconv×ΔT（15）

因為單位協商時間ΔT取決于多機器人系統的通信與計算能力，所以在具體系統中往往為一定值。減少協商次數ktotal或總協商時間ttotal能夠快速獲取收斂值，但是有不收斂的風險。提高協商次數ktotal或總協商時間ttotal有利于獲取準確的收斂值但是協商結果刷新的速度變慢。因此需要根據實際情況綜合決定ktotal與ttotal。

在重復進行的協商過程中，ktotal在任務開始前已經給定。然而，達到平均一致性所需的協商次數K1通常大于達到最大一致性所需的協商次數K2。因此，設計K1=ktotal而且K1=q×K2（q為正整數）來組合不同類型的協商結果。

為了確保所有機器人在給定的時刻執行一致性計算，即迭代時刻相等tki=tkj，同時確保完全分布。k值通過掛鐘時間求取，即指定第k次協商的協商迭代時刻，如式（16）所示。

2.2 集中式多機器人巡邏算法EAIG

本節設計了一種集中式多機器人巡邏算法。當機器人到達起始節點或目標節點時，它將采用以下三步選擇目標點。首先，計算該節點所有鄰接節點NG1（vi）的效用度U1。然后，遍歷所有其他機器人的意圖節點序列It，如果存在意圖節點是該節點的鄰居節點，則該鄰居節點效用度歸零。從而得到決策用的效用度U并且避免機器人之間的沖突。最后，從鄰接節點中選擇效用度最高的節點作為目標節點。從而使得每個機器人基于全局信息獨立在線決策。機器人在決策后也會向所有其他機器人發送到達信息和意圖信息，使每個機器人獲知全局信息。整個過程如圖5所示。

采用期望平均空閑時間和期望瞬時空閑時間構造效用函數。基于瞬時空閑時間定義，期望瞬時空閑時間定義為

Iviexp（t）=t－tlast+cost/VEL（17）

其中：cost代表前往目標點的距離；VEL代表機器人的平均速度。

根據平均空閑時間定義，用訪問次數表示如下：

其中：ttotal表示機器人總計巡邏時間。用Δtexception表示機器人宕機、充電等行為所占的時間，那么ttotal可以表示為

ttotal=t－t0－Δtexception（19）

其中：t0代表頂點第一次被訪問的時刻，也代表機器人的啟動時刻。定義期望平均空閑時間如下：

期望瞬時空閑時間和期望平均空閑時間反映了機器人未選擇頂點vi作為目標點時可能發生的平均空閑時間和瞬時空閑時間。因此機器人傾向于前往潛在空閑時間更高的目標點。效用值U1表示為

其中：U1為大于零的正數；α，β為比例因子。

采用意圖信息避免兩個機器人訪問同一個節點，減小機器人之間的沖突，得到最終決策用的效用度U。當機器人ri的意圖節點為vj時，Itri=vj，反之Itrivj。當一帶機器人的其中一個對某節點存在意圖時，其向所有巡邏機器人發布意圖信息Itri=vj。當其他機器人收到該信息后，其在決策時將該節點效用度歸零。由于效用度是由期望平均空閑時間和期望瞬時空閑時間構造的大于零的值，所以鄰居機器人會選擇其余節點作為目標節點，避免了兩個機器人之間的潛在沖突。機器人ri存儲著所有其他機器人的意圖節點序列It={Itr1=vi1 Itr2=vi2 … Itrm=vim}，簡記為It={vi1 vi2 … vim}。用于決策的機器人ri對鄰居節點vi的效用值U最終表示為

本文所提的集中式巡邏算法稱為基于全局信息的期望平均空閑和期望瞬時空閑算法（expected average idleness and expected idleness of global information，EAIG），算法偽代碼如下所示。

算法1 基于全局信息的期望平均空閑和期望瞬時空閑的算法

2.3 分布式多機器人巡邏算法EAIL-C

2.3.1 算法描述

基于上述離散時間一致性算法的實現和集中式多機器人巡邏算法EAIG建立完全分布式多機器人巡邏算法。與EAIG的不同點有兩個：a）機器人隨時都在同鄰居機器人進行協商以刷新收斂信息，替代了到達目標節點時向所有機器人的廣播行為;b）決策所用的信息是局部信息而不是全局信息。機器人的協商過程和決策過程是相互關聯的兩個過程，整個過程如圖6所示。

在協商過程中，當k=0時，機器人通過本地信息初始化其協商值。用列向量表示所有的協商值，并設計在一條協商消息中。在每個單位協商時間ΔT期間，此協商消息是唯一的。協商消息將向鄰居機器人多次廣播，等待一致性迭代計算。然后通過離散時間一致性計算得到下一個單位協商時間更新的協商值和收斂值。最后，在k=ktotal時刷新協商結果并儲存在收斂值中。當需要進行決策時，機器人基于收斂的協商信息對全局信息進行估計，采用估計信息替代全局信息并計算效用值。與EAIG類似，機器人從鄰接節點中選擇效用值最大的節點作為目標點。

EAIG的全局信息和EAIL-C中基于協商信息預估的全局信息對比于表1中。協商信息預估全局信息的過程見下節。

式（23）～（27）與式（17）～（22）類似，設計了分布式多機器人巡邏算法EAIL-C計算各節點效用值的公式。與EAIG的決策邏輯相同，效用值最高的鄰居節點將成為目標節點。

采用最近一次訪問時刻估計值替代基于全局信息的最近一次訪問時刻，期望瞬時空閑時間定義為

Ivi exp（t）=t－testj+cost/VEL（23）

采用節點訪問次數估計值替代節點總訪問次數，平均空閑時間表示為

定義期望平均空閑時間如下：

效用值U1如式（26）所示，一般情況下，U1為大于零的正數。

采用節點意圖估計值序列Itest替代每個機器人的意圖序列It。機器人ri對節點vj的二元的意圖估計值Itesti_j，簡記為Itestj。當Itestj=1時，存在機器人對該節點的訪問意圖。當Itestj=0時，沒有機器人計劃訪問該節點。當一帶機器人的其中一個對某節點存在意圖時，其意圖協商信息通過鄰居機器人之間的相互協商影響到這一帶的所有機器人的協商信息，并進一步影響到這一帶機器人對全局信息的預估值Itestj。當其余機器人根據協商信息預估值判斷該節點時，該節點的效用度歸零。由于其他節點的效用度大于零，所以機器人不再選擇該節點作為目標節點，避免了機器人之間的潛在沖突。機器人存儲并通過協商信息預估著整張地圖所有節點的意圖估計序列Itest={Itestv1 Itestv2 … Itestvn}。該估計序列由協商信息估計得到并經由協商過程不斷刷新，與機器人數量無關，是局部信息。用于決策的機器ri對鄰居節點vj的效用值U最終表示如下：

上述完全分布式巡邏算法稱為基于局部信息的期望平均空閑和期望瞬時空閑的算法，簡稱為EAIL-C（expected average idleness and expected idleness of local information-cycled negotiation）。該算法的偽代碼如算法2所示。一致性協商包括時間檢查程序（time check）、一致性消息發布程序（publish consensus message）、一致性消息接收程序（receive consensus message）和節點到達程序（goal reached）。時間檢查過程在給定時間通過ROS掛鐘時間回調來計算新的協商值，而另外兩個過程用于信息傳輸。巡邏行為包含在節點到達程序中，當機器人到達一個節點時被觸發。

算法2 基于局部信息的期望平均空閑和期望瞬時空閑的算法

2.3.2 協商信息設計與全局信息預估

本節介紹了協商過程和估計全局信息的過程。鑒于固定拓撲能夠可重復地描述信息的協商過程，本節示意圖中機器人之間的關系均由固定拓撲描述，如圖7所示。

為了預估EAIG的全局信息，設計機器人ri對節點vj的協商信息。EAIL-C的協商信息初始值、協商值、收斂值如表2所示。其中，協商信息初始值由每個機器人根據自身的節點訪問情況賦值。經過一致性計算得到協商值，協商完成后保存收斂值。每當機器人需要決策時，基于協商值和收斂值計算全局信息的估計值。

采用最大一致性協商K2次得到機器人最近一次訪問節點的時刻tlastj的收斂值t_delastj。機器人之間的協商過程如圖8所示，用收斂值代表預估的最近訪問時刻，即testj=t_delastj。

當節點vj是機器人ri的目標節點時Itj=1，否則Itj=0。采用平均一致性協商K2次獲取節點意圖收斂值Itcoj，易知，0≤Itcoj≤1。當且僅當Itdej=0并且Itcoj=0時沒有機器人計劃訪問該節點。從而通過式（28）得到估計的意圖信息Itestj。最大一致性也在這里有效。協商過程如圖9所示。

采用平均一致性協商K1次得到節點vj的訪問次數kj的收斂值kdej，kdej反映了節點的平均訪問次數。然而，平均一致性協商需要更多的協商時間來獲得節點訪問次數的收斂值，而在協商期間節點可能被訪問。這將導致協商值無法及時刷新。因此，有必要設計一個輔助協商變量以估計更新的全局信息，即設計一種基于收斂協商和趨勢協商相結合的雙重協商策略。結合收斂協商和趨勢協商的價值，準確地估計全局信息。設計節點訪問次數趨勢ktrj作為機器人ri關于節點vj的協商變量，表示在協商期間節點是否被訪問。在一輪kj協商初始化之后，如果機器人ri訪問節點vj，那么ktrj=1，否則ktrj=0。采用平均一致性協商K2次獲取節點訪問次數趨勢收斂值ktrdej。與Itcoj和Itdej類似，節點是否被訪問是由ktrcoj和ktrdej來確定。因為節點訪問趨勢不能反映多次訪問，例如在同一協商中訪問了節點兩次，所以協商周期ttotal需滿足

ttotal

其中：Imin表示最小空閑時間。

為了結合kdej和ktrdej，需要估計機器人數量。機器人ri的協商變量mi_k表示機器人rk是否存在于協商中，通過式（30）初始化。采用平均一致性協商K2次獲取協商值mcoi_k，最大一致性也可以通過收斂值mdei_k是否等于0判斷機器人rk是否參與了協商。進而可以由式（31）得到參與協商的機器人數量mi。

其中：「·表示向上取整。因此，機器人數量的協商過程如圖10所示。

因此節點訪問次數由式（32）估計，節點訪問次數的協商過程如圖11所示。

Itcoj、ktrcoj和mcoi_k只需要確定收斂值是否等于零，因此最大一致性和平均一致性都有效。

2.3.3 信息協商中的延遲

離散時間一致算法的實現過程具有延遲效應，包括延遲開始和延遲結束。以意向協商為例，如圖12（a）所示，當機器人4計劃訪問節點0并在第566.2 s以1初始化其Itco4_0時，其鄰居的協商信息依次受到影響，需要3個單位協商時間（0.6 s）才能影響到最遠的鄰居1號機器人Itco1_0。即Itco1_0在第566.8 s時受到影響。考慮到協商值會周期性初始化，實際延遲可能會更長。當兩個機器人同時到達相鄰的目標節點時，延遲開始會導致兩個機器人選擇與目標節點相同的節點，從而導致沖突。另一方面，如圖12（b）所示，當意圖信息在第584.2 s消失后，延遲效應阻止了協商意圖在第585.2 s前返回到零。延遲結束阻止機器人選擇剛剛被另一個機器人訪問的節點，從而對計劃的路徑造成影響。由于機器人的沖突，延遲開始的影響遠遠超過延遲結束。所以，應盡量避免延遲開始。

解決延遲協商意圖引起沖突的一種可能的解決方案是將鄰居意圖和協商意圖結合起來。其原因是，機器人選擇了一個相鄰的節點作為目標節點，因此該潛在的沖突機器人位于其目標節點的相鄰節點上。只要機器人的通信半徑能夠覆蓋相鄰節點的相鄰節點，它就可以直接與潛在的沖突機器人通信，獲取它們的本地意圖信息。

另一方面，考慮到跟隨行為的風險，不能不考慮鄰居意圖而單獨使用協商意圖。跟隨行為意味著兩個機器人總是一個接一個作出相同的選擇，導致巡邏效果降低。其原因在于，鄰居離開某節點的局部意圖是準確的，而鄰居剛剛訪問該節點的信息是延遲的。因此，跟隨者機器人不知道這個節點剛剛被訪問，并且總是用相同的決策信息作出與前一個機器人相同的選擇。當機器人之間的關系固定，如圖7所示，且地圖拓撲的各邊長度相等時，跟隨問題變得更加明顯，特別是在機器人1和4之間。通信半徑內鄰居間的通信使得可能沖突的兩個機器人之間產生了直接的意圖信息交互，提高了意圖傳輸的速度，從而解決了協商信息延遲的問題。當機器人進行決策時，如果協商信息指示目標節點存在訪問意圖（Itestj=1），或者接收到鄰居機器人意圖訪問該節點的信息，那么機器人的效用值歸零，不會將該節點作為目標節點。

3 仿真實驗與結果

仿真實驗的目的是通過模擬一個真實的環境從而比較不同的多機器人巡邏算法，并確認EAIL-C是否具有與EAIG相似的特性。文獻［23］設計了基于ROS和Stage的patrolling_sim功能包以進行多機器人巡邏策略的仿真開發驗證，不斷添加新的巡邏算法并更新平臺。功能包采用ROS開源導航包進行導航，可直接部署在基于ROS的機器人上實現應用。本文基于patrolling_sim功能包添加了EAIG、EAIL-C兩個新算法并對相關文件進行了修改以適應算法，從而驗證算法，并同功能包已有算法進行對比。以ROS移動機器人為對象模擬實際環境應用場景進行相關仿真實驗。

3.1 仿真設置

采用兩種地圖（cumberland和grid）對巡邏算法進行評價對比，如圖13和表3所示，在實驗開始前地圖及其拓撲已知，其中，grid地圖連通性更好且所有節點之間的距離相等。

考慮到機器人之間的關系變化，基于通信半徑約束確定機器人之間的關系。雖然較低的通信半徑意味著對巡邏機器人的要求較低，但應考慮鄰居的意圖以避免發生沖突。因此機器人的通信半徑應至少覆蓋到鄰居節點的鄰居節點。不同地圖的實驗通信半徑Rset應大于最小值Rmin，如表4所示。

基于通信半徑建立了兩種機器人關系。第一個名為EAIL-C1，機器人只使用協商信息，因為當兩個機器人基于通信半徑建立關系時，延遲啟動引起的沖突與固定拓撲相比并不明顯。第二個名為EAIL-C2，同時考慮了通信半徑以內的鄰居意圖和協商意圖，以最大程度減少沖突。一個固定的拓撲結構有利于滿足一致性的收斂條件。因此，本文認為由固定拓撲所描述的機器人之間的關系是基于通信半徑的交換拓撲的弱化，在實驗中不考慮固定拓撲。

另外：a）EAIL-C1只采用協商信息進行決策；b）EAIL-C2采用協商信息以及通信半徑以內的鄰居意圖信息共同決策。

采用四個機器人進行實驗，機器人的平均速度VEL取值1 m/s。算法參數設置為：α=1、β=1、ε=1/5、K1=35、K2=5。每組仿真實驗持續1 h并重復三次。在通過方差分析檢驗（ANOVA）的條件下，為每個算法選擇三個仿真結果。各算法的p值均大于0.1，表示相同分布的概率較高。采用監控節點收集信息和求解評價指標。

用于對比的算法包括SEBS、DTAP，這兩種算法都可以反映EAIG和EAIL-C的特性。算法對比如表5所示。

3.2 巡邏過程及巡邏算法對比

多機器人巡邏過程如圖14所示，圖中四個機器人在各自執行巡邏任務。通過記錄單個機器人巡邏過程中的位置，繪制其1 h軌跡圖，如圖15所示。

cumberland地圖的實驗結果如表6所示，EAIG算法的全圖空閑時間平均值IGavg均介于SEBS和DTAP之間，接近于SEBS。而EAIG的全圖空閑時間標準差IGstddev、全圖空閑時間最大值IGmax大于SEBS和DTAP。EAIL-C繼承了EAIG的算法特性，它的平均空閑時間略有增加，但總體上與EAIG處于同一水平。由于協商信息的延遲效應，EAIL-C1和EIAL-C2的干擾率均略高于EAIG。在鄰居意圖的影響下，EAIL-C2的干擾率低于EAIL-C1。

grid地圖的結果如表7所示，EAIG的全局平均空閑時間IGavg優于DTAP，略優于SEBS。EAIG的全圖空閑時間標準差、全圖空閑時間最大值與SEBS和DTAP處于同一水平。因此，EAIG的性能優于SEBS和DTAP。因為grid地圖的連通性比cumberland地圖更好，所以grid地圖的干擾率比cumberland高，其性能受到的影響更大。EAIL-C1和EAIL-C2的全局平均空閑時間IGavg與EAIG的水平相同。EAIL-C1和EAIL-C2的空閑時間標準差IGstddev和最大空閑時間IGmax均高于EAIG，而EAIL-C2的性能優于EAIL-C1，這是由于EAIL-C2具有更準確的意圖信息，帶來更低的干擾率和更好的性能。總體來說，EAIL-C的巡邏效果與EAIG非常接近。

使用箱線圖分析不同節點的平均空閑時間，如圖16、17所示。在cumberland和grid地圖中，SEBS的平均空閑時間都低于DTAP，但存在許多異常值。DTAP以增加節點的平均空閑時間為代價減少了異常值。EAIG在保持了較低的平均值水平的基礎上異常值較少，因此節點的平均空閑時間表現更好。同時，EAIL-C具有與EAIG相似的特征，而EAIL-C2在grid地圖的表現優于EAIL-C1。

綜上所述，在本地信息和鄰居協作的支持下，EAIL-C取得了與EAIG相似的性能。避免了全局信息，并考慮了通信約束。當地圖的拓撲連通度較低時，EAIL-C就可以基本反映EAIG的算法特征，并在一定程度上取代原算法EAIG。當圖的拓撲連通性較高時，EAIL-C的干擾率越高。在通信半徑內鄰居的局部意圖的幫助下，EAIL-C2取得了比EAIL-C1更穩定的巡邏效果。

3.3 一致性算法的性能確認

一致性算法的收斂性對性能起著重要作用。因此，本節使用cumberland地圖中EAIL-C1的數據來確定其收斂性。本小節分析了協商K2次的意圖信息和協商K1次的節點訪問次數。

機器人并不總是能保持完全的連接。機器人之間連邊的數量對收斂結果有不可否認的影響，因此，監控節點每秒鐘記錄一次每個機器人的位置。不同數量的連接邊對應的時間比例如表8所示，大約30%的時間有3條或更多的邊，這意味著這四個機器人保持完全連接，可以準確地估計全局信息。大約35%的時間里，有兩條邊，即兩個或三個機器人連接起來，它們的信息被用來估計全局信息。

意圖協商是趨勢協商，其目標是確定協商值是否等于零，并估計對應的全局信息。通過在每個單位協商時間ΔT處存儲估計的全局信息和真實的全局信息并進行比較，確認所估計的意圖是否準確。估計的全局意圖Itestj受到信息協商延遲和機器人之間關系的影響。結果顯示，94.32%的數據與全局信息一致，如表9所示。這超過了準確估計全局信息的時間35%。原因是單個節點超過85%的時間是沒有機器人訪問的意圖的。

節點訪問次數的協商是收斂協商，其目標是得到收斂值kdej。收斂性受到一致性收斂速度和機器人之間關系的影響。當k=K1時計算kconvi_j，以檢查協商收斂情況，如式（33）所示。

如果kconvi_j< 0.25，則認為它是收斂的。結果表明，95%的協商滿足收斂條件，如表10所示。

3.4 不同機器人數量和通信距離下的性能驗證

本節對EAIL-C2算法進行進一步性能驗證。考慮2，4，6，8四種機器人數量進行對比。考慮避免沖突的最小通信半徑、覆蓋全圖的最大通信半徑以及介于兩者之間的通信半徑。grid地圖對12 m、24 m、36 m三種通信半徑進行對比，cumberland地圖對16 m、40 m、64 m三種通信半徑進行對比，其余參數與上節仿真設置相同。考慮grid、cumberland兩種地圖環境。

圖18、19分別展示了SEBS、DTAP、EAIG和EAIL-C2算法在grid和cumberland兩種地圖中的全圖空閑時間平均值IGavg和標準差IGstddev隨時間的變化，其在1 500 s以內穩定。因此，本節仿真時間為60 min。每組仿真實驗至少重復3次，取其平均值進行對比。

grid地圖的結果如表11、12所示。其中，表11對比了EAIL-C2在不同機器人數量和通信半徑條件下的巡邏效果。在同一通信半徑下，隨著機器人數量的提升，全圖平均空閑時間、全圖空閑時間標準差下降，機器人之間的干擾率上升。全圖空閑時間最大值在機器人數量為2時出現。因此，機器人數量對巡邏效果有重要作用。而隨著機器人通信半徑的增加，全圖平均空閑時間、全圖空閑時間標準差、機器人之間的干擾率沒有明顯區別。因此，算法EAIL-C2受通信半徑的影響較小。

表12展示了不同機器人數量下對比算法的評價指標。在不同機器人數量下，EAIG和EAIL-C2的全局平均空閑時間均優于DTAP，接近于SEBS。隨著機器人數量的增加，各個算法的全圖空閑時間標準差隨之下降。在干擾率方面，隨著機器人數量的增加，機器人之間的干擾率不斷上升。相比之下，SEBS的干擾率上升明顯，而DTAP、EAIG、EAIL-C2基本處于同一水平。EAIL-C2的干擾率高于原算法EAIG。因此，EAIL-C2在各個條件下的評價指標均略弱于基于全局信息的EAIG算法，但差距不大。

EAIL-C2在cumberland地圖的實驗結果如表13所示，機器人數量對實驗結果的影響大于通信半徑的影響。在同一通信半徑下，隨著機器人數量的提升，全圖平均空閑時間、全圖空閑時間標準差下降，機器人之間的干擾率上升。全圖空閑時間最大值出現在機器人數量為2時，隨著機器人數量的增加呈現遞減趨勢。而隨著機器人通信半徑的增加，全圖平均空閑時間、全圖空閑時間標準差、機器人之間的干擾率沒有明顯區別。因此，算法EAIL-C2受通信半徑的影響較小。

表14展示了對比算法的評價指標。在不同機器人數量下，EAIG和EAIL-C2的全局平均空閑時間均優于DTAP，略弱于SEBS。EAIG和EAIL-C2的全圖空閑時間標準差大于SEBS和DTAP。隨著機器人數量的增加，所有算法的全圖平均空閑時間、全圖空閑時間標準差下降，機器人之間的干擾率上升。最大干擾率出現在八個機器人的SEBS算法中，而EAIG的干擾率介于DTAP和SEBS之間。EAIL-C2的干擾率高于EAIG，其余指標和EAIG接近，基本處于同一水平。

圖20展示了不同機器人數量和不同通信半徑下的各個節點的平均空閑時間箱線圖。在grid地圖中，SEBS的平均空閑時間都低于DTAP，但存在許多異常值。EAIG的平均值接近于SEBS，同時異常值較低。因此節點的平均空閑時間表現更好。同時，EAIL-C在不同半徑下具有與EAIG相似的分布。在cumberland地圖中，EAIG的效果介于SEBS和DTAP之間，接近于SEBS，其異常值同樣較少。EAIL-C2的效果與EAIG類似，受通信半徑影響較小。

綜上所述，EAIG相比DTAP具有更低的平均空閑時間，相比SEBS異常值更少，具有一定優勢。EAIL-C具有和EAIG類似的算法特點，能夠基本達到EAIG的算法性能。

4 結束語

本文采用離散時間一致的方法實現了完全分布式多機器人巡邏算法EAIL-C，并與原有的集中式巡邏算法EAIG等巡邏算法進行了比較。算法考慮了通信半徑和局部信息的約束條件。在每個周期中都可以獲得最新的協商結果，并且協商信息獨立于特定的機器人。機器人之間的關系會根據通信半徑和機器人位置的變化而變化。采用仿真器Stage對算法進行了仿真和比較，驗證了所提算法EAIL-C具有與原算法EAIG相似的特性和性能。EAIL-C算法為后續實現更大規模的機器人集群提供了思路，所提出的趨勢協商和收斂協商的協商方法可以擴展到其他集中式巡邏算法，以實現完全分布。所提算法適用于巡邏范圍大且通信半徑有限的情況。例如：森林火災實時監控、海洋污染防控、邊境線巡邏等。

在未來的多機器人分布式巡邏算法的研究中，可以考慮以下兩個方向：采用更優秀的離散時間一致性算法來加速協商速度，這意味著更低的Ktotal；綜合考慮機器人的位置和通信半徑、機器人之間的關系維持和巡邏任務的完成，設計出與實際情況關聯更緊密的完全分布式巡邏算法。

參考文獻：

［1］Huang Li，Zhou Mengchu，Hao Kuangrong，et al. A survey of multi-robot regular and adversarial patrolling［J］. IEEE/CAA Journal of Automatica Sinica，2019，6（4）： 894-903.

［2］Chen Feiran，Chen Bin，Zhu Zhengqiu，et al. A cost-beneficial area-partition-involved collaborative patrolling game in a large-scale chemical cluster［J］. Process Safety and Environmental Protection，2021，145： 71-82.

［3］Machado A，Ramalho G，Zucker J D，et al. Multi-agent patrolling： an empirical analysis of alternative architectures［J］. Lecture Notes in Computer Science，2003，2581（1）： 81-97.

［4］武麗霞. 多機器人系統分布式巡邏算法設計及實驗驗證［D］. 蘭州： 蘭州交通大學，2019. （Wu Lixia. Distributed patrol algorithm design and experimental verification for multi-robot system［D］. Lanzhou： Lanzhou Jiaotong University，2019.）

［5］史天伊. 多機器人系統巡邏分布式算法研究［D］. 蘭州： 蘭州交通大學，2021. （Shi Tianyi. Research on distributed patrol algorithm of multi-robot system［D］.Lanzhou：Lanzhou Jiaotong University，2021.）

［6］趙云濤，李宗剛，杜亞江. 基于最大空閑時間的分布式巡邏機器人數量優化［J］. 模式識別與人工智能，2020，33（4）： 375-382. （Zhao Yuntao，Li Zonggang，Du Yajiang. Team size optimization for distributed patrol of multi-robot systems based on maximum idle time［J］. Pattern Recognition and Artificial Intelligence，2020，33（4）： 375-382.）

［7］霍耀彥，李宗剛，高溥. 基于節點重要度的多機器人分布式巡邏策略［J］. 計算機應用研究，2022，39（2）： 510-514. （Huo Yaoyan，Li Zonggang，Gao Pu. Distributed multi-robot patrolling stra-tegy based on importance of nodes［J］. Application Research of Computers，2022，39（2）： 510-514.）

［8］Yan Chuanbo，Zhang Tao. Multi-robot patrol： a distributed algorithm based on expected idleness［J］. International Journal of Advanced Robotic Systems，2016，13（6）： 1-12.

［9］Portugal D，Rocha R P. Distributed multi-robot patrol： a scalable and fault-tolerant framework［J］. Robotics and Autonomous Systems，2013，61（12）： 1572-1587.

［10］王通，黃攀峰，董剛奇. 啟發式多無人機協同路網持續監視軌跡規劃［J］. 航空學報，2020，41（S1）： 723-753. （Wang Tong，Huang Panfeng，Dong Gangqi. Cooperation path planning of multi-UAV in road-network continuous monitoring［J］. Acta Aeronautica et Astronautica Sinica，2020，41（S1）： 723-753.）

［11］Portugal D，Rocha R P. Cooperative multi-robot patrol with Bayesian learning［J］. Autonomous Robots，2016，40（5）： 929-953.

［12］Farinelli A，Iocchi L，Nardi D. Distributed on-line dynamic task assignment for multi-robot patrolling［J］. Autonomous Robots，2017，41（6）： 1321-1345.

［13］Huang Li，Zhou Mengchu，Hao Kuangrong，et al. Multirobot cooperative patrolling strategy for moving objects［J］. IEEE Trans on Systems，Man，and Cybernetics Systems，2023，53（5）： 2995-3007.

［14］Ahmadian N，Lim G J，Torabbeigi M，et al. Smart border patrol using drones and wireless charging system under budget limitation［J］. Computers & Industrial Engineering，2022，164： 107891.

［15］Aggravi M，Sirignano G，Giordano P R，et al. Decentralized control of a heterogeneous human-robot team for exploration and patrolling［J］. IEEE Trans on Automation Science and Engineering，2022，19（4）： 3109-3125.

［16］Scherer J，Schoellig A P，Rinner B. Min-max vertex cycle covers with connectivity constraints for multi-robot patrolling［J］. IEEE Robotics and Automation Letters，2022，7（4）： 10152-10159.

［17］Caraballo L E，Diaz-banez J M，Fabila-monroy R，et al. Stochastic strategies for patrolling a terrain with a synchronized multi-robot system［J］. European Journal of Operational Research，2022，301（3）： 1099-1116.

［18］Ren W，Beard R W. Distributed consensus in multi-vehicle cooperative control： theory and applications［M］. London： Springer-Verlag，2008.

［19］紀良浩，王慧維，李華青. 分布式多智能體網絡一致性協調控制理論［M］. 北京： 科學出版社，2015. （Ji Lianghao，Wang Huiwei，Li Huaqing. Multi-agent networks distributed consensus cooperative control theory［M］. Beijing： Science Press，2015.）

［20］Olfati-Saber R，Murray R M. Consensus problems in networks of agents with switching topology and time-delays［J］. IEEE Trans on Automatic Control，2004，49（9）： 1520-1533.

［21］Moreau L. Stability of multiagent systems with time-dependent communication links［J］. IEEE Trans on Automatic Control，2005，50（2）： 169-182.

［22］Ren W，Beard R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies［J］. IEEE Trans on Automatic Control，2005，50（5）： 655-661.

［23］Portugal D，Iocchi L，Farinelli A. A ROS-based framework for simulation and benchmarking of multi-robot patrolling algorithms［M］// Koubaa A. Robot Operating System. Cham： Springer，2019： 3-28.