基于Vine-Copula的高土石壩變形監(jiān)控模型研究

陳天賜 李艷玲 張芳 陳梟

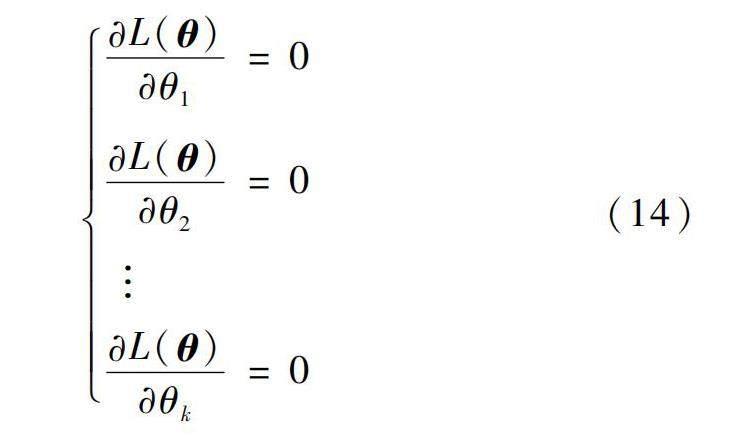
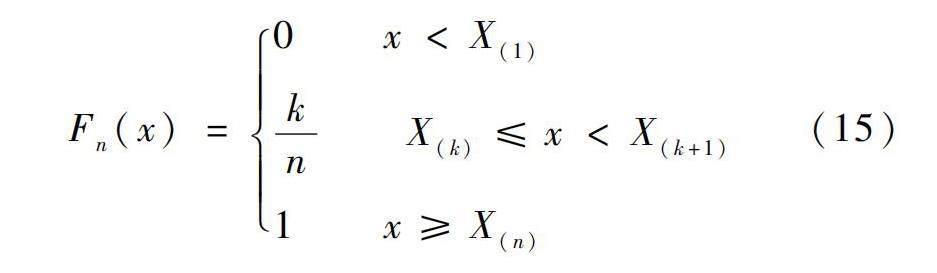
摘要：針對高土石壩變形監(jiān)控模型主要基于單一測點，無法定量考慮測點空間關聯(lián)性的問題，構建了基于Vine-Copula的變形監(jiān)控模型，并提出了基于蒙特卡洛隨機抽樣法的空間置信域預警閾值設置方法。在模型構建過程中，充分考慮了多測點之間的時序特性和空間相關性，利用Vine-Copula方法對變形數據進行精確建模和分析，以揭示高土石壩變形的整體趨勢。同時，通過蒙特卡洛隨機抽樣法確定了空間置信域，為預警閾值的設定提供了科學依據。工程實踐表明：該模型模擬結果能夠準確反映高土石壩變形的整體趨勢，具有較高的合理性和精度，有效實現(xiàn)了監(jiān)測效應量向高土石壩空間全域的拓展。研究成果可為高土石壩安全監(jiān)控提供新的思路和方法，具有重要的理論意義和實踐價值。

關 鍵 詞：高土石壩；變形監(jiān)控模型；Vine結構；Copula函數；空間置信域

中圖法分類號：TV698.1

文獻標志碼：A

DOI：10.16232/j.cnki.1001-4179.2024.05.027

0 引 言

高土石壩變形是科學分析大壩安全性態(tài)的基礎，合理構建高土石壩變形監(jiān)控模型是實現(xiàn)大壩運行安全在線監(jiān)控的關鍵。統(tǒng)計模型、確定性模型和混合模型^［1-3］是最常用的3種變形監(jiān)控模型。近年來，隨著機器學習技術的發(fā)展，神經網絡^［4-5］、支持向量機^［6-7］等方法相繼應用于土石壩變形監(jiān)控模型構建，單點監(jiān)控模型的合理性和適用性得到了較大提升。但單點監(jiān)控模型僅能反映測點所在位置的局部變形性態(tài)，無法反映變形整體趨勢，且易因設備故障、測量誤差等出現(xiàn)局部偏離而導致對大壩整體安全性態(tài)的誤判和虛警。

因此，國內外不少學者開始對大壩變形監(jiān)控模型進行探索，一些結合多測點的監(jiān)控模型開始出現(xiàn)。任秋兵等^［8］考慮到空間中任意兩個測點存在一定的關聯(lián)度，提出了基于門控循環(huán)單元神經網絡結合軟注意力機制的大壩變形動態(tài)監(jiān)控模型；蔡忍等^［9］運用投影尋蹤法給多測點賦予不同的權重，建立了綜合大壩變形監(jiān)控模型，實現(xiàn)了對大壩斷面變形性態(tài)的監(jiān)控；王少偉等^［10］融入同類多測點數據，構建了基于主成分分析法的變形監(jiān)控模型，實現(xiàn)了對大壩整體變形的快速診斷。總的來說，多點空間監(jiān)控模型能夠實現(xiàn)對大壩整體的監(jiān)控，具有一定優(yōu)勢，但已有的方法還不夠成熟，有待進一步研究。目前Vine-Copula模型已經應用于水文、金融、投資等^［11-13］各個領域，但在大壩變形監(jiān)控模型領域應用還較為少見，具有較大研究價值。

本文考慮多測點時序特性和空間相關性，引入Vine-Copula聯(lián)合分布函數構建高土石壩多測點變形監(jiān)控模型，并將其運用于SBX高面板堆石壩變形監(jiān)控。

1 高土石壩變形監(jiān)控模型構建

1.1 基本原理

綜合考慮同類同部位測點變形的相關性和協(xié)調性，本文引入了“藤”（Vine）結構和“連接函數”（Copula）的概念，將具有空間一致性的多測點利用Vine結構和Copula函數連接起來，建立測線或斷面多測點聯(lián)合的變形監(jiān)控模型，并通過監(jiān)控其聯(lián)合分布函數變化特性，實現(xiàn)對大壩同一測線或斷面的整體變形特性監(jiān)控。一般地，大壩變形正常時，其同一測線或斷面的多測點聯(lián)合分布函數在其空間置信域內，而當其出現(xiàn)整體變形時，其多測點聯(lián)合分布函數將偏離空間置信域。因此，構建Vine-Copula土石壩變形監(jiān)控模型的基礎是計算多測點的空間聯(lián)合分布函數。

Sklar^［14］指出，一系列隨機變量組成的聯(lián)合分布可以分解成單一變量的邊緣分布和單一變量間的Copula連接函數。由于單一變量的邊緣分布是一定的，因此一個聯(lián)合分布的相關性完全取決于Copula函數。傳統(tǒng)的Copula函數對于聯(lián)合高維變量費時費力且不宜開展，因此Aas等^［15］提出了Pair Copula的概念，利用鏈式法可將多個隨機變量的聯(lián)合概率密度函數（PDF）分解為所有單個變量的邊緣PDF和對應幾個Copula 密度函數的乘積。

假定{x₁，x₂，…，x_n}是一變形單測點歷史實測值序列，利用核密度估計法計算單測點測值的概率密度函數，如式（1）所示。

式中：x為單測點測值；x_i為測點歷史實測值；n為單測點歷史測值的數量；K為一個非負函數，稱為核函數，引用最常用的Gussian核函數進行計算；h為核密度估計的帶寬，利用經驗公式進行計算；σ^為單測點歷史測值序列的標準差。

對式（1）積分可得到式（4），計算出各測點歷史實測值的概率邊緣分布函數F₁（x₁），F(xiàn)₂（x₂），…，F(xiàn)_n（x_n），分別用u₁，u₂，…，u_n表示。

根據Sklar定理，存在連接函數C（·）使得各測點聯(lián)合分布F（x₁，x₂，…，x_n）滿足式（5），各測點多元聯(lián)合密度函數f（x₁，x₂，…，x_n）可表達為式（6）。

為連接函數C（·）的密度函數；f₁，f₂，…，f_n為F₁（x₁），F(xiàn)₂（x₂），…，F(xiàn)_n（x_n）各測點邊緣分布的密度函數。

根據條件概率乘法公式，式（6）可以轉化為式（7），結合式（6）和式（7），可得兩個變量的聯(lián)合概率密度f（x₁|x₂），如式（8）所示，任何一個條件密度函數可分解為式（9）。

式中：v_j代表n維向量v中的分量，v_-j代表v中去除v_j后的n-1維分量。

一個n維的Vine-Copula模型結構由n-1棵樹和n（n-1）/2條邊組成，為了將Pair Copula函數之間的關系及各個變量的相關結構更好地表達出來，引入“正則藤”（R-Vine）^［16］概念。結合式（7）和式（9）得到R-Vine 模型的聯(lián)合概率密度公式：

式中：x_i為測點歷史實測值，n表示節(jié)點數，即變量個數；e表示邊；E=［E₁，E₂，…，E_n-1］，E_i代表第i棵樹中所有邊組成的集合；j（e）、k（e）為邊e的兩個節(jié)點；D（e）為j（e）和k（e）之間的連接條件；c_{j（e），k（e）|D（e）}為第i棵樹中j、k的邊e對應的Pair Copula密度函數；F（x_j（e）|x_D（e））和F（x_k（e）|x_D（e））表示條件分布函數。

1.2 模型構建流程

基于Vine-Copula的變形監(jiān)控模型構建可使用同一測線或斷面的多測點歷史監(jiān)測數據，假設大壩某測線或斷面上有n個變形測點，利用這n個變形測點的歷史實測值建立變形監(jiān)控空間模型，大壩Vine-Copula變形監(jiān)控模型的建模流程見圖1。

1.2.1 單測點概率分布計算

依據n個變形測點的歷史實測值，利用1.1節(jié)中式（1）和式（4）計算單測點測值的概率分布函數。

1.2.2 Vine Copula模型結構優(yōu)選

常用的Vine結構有R-Vine結構、D-Vine結構和C-Vine結構3種。R-Vine結構適用于任何相關結構，具普適性，但當測點數量較大時，R-Vine結構的數量呈現(xiàn)急速增漲^［17］，計算復雜程度高且效率低。D-Vine結構和C-Vine結構是R-Vine結構的特殊類型，能夠在一定程度上提高計算效率。C-Vine為一個變量發(fā)散關聯(lián)其他變量的結構，適用于具有主導變量的結構；D-Vine為串聯(lián)的直線型結構，適用于描述有臨近關系的相關結構。以六維Vine結構為例，R-Vine、C-Vine和D-Vine的結構，如圖2所示。

為充分考慮各測點的關聯(lián)性，同時盡量使模型簡單高效，實際應用中常采用最大生成樹（MST）法和計算測點間的肯德爾相關系數（τ）來確定變形監(jiān)控空間模型的最優(yōu)Vine結構。首先計算Kendall系數τ，對各測點間的相關性進行初步分析，選用較優(yōu)R-Vine結構建模；然后利用最大生成樹（MST）法選擇每一棵樹結構。最優(yōu)Vine結構則能保證每棵樹Kendall系數τ的絕對值之和最大。Kendall系數τ是相關性度量指標，介于-1～1之間，其絕對值越接近1，表示相關程度越強。

設X={x₁，x₂，…，x_n}和Y={y₁，y₂，…，y_n}分別為兩測點的歷史實測值序列，（x_i，y_i）和（x_j，y_j）分別為i、j時刻兩測點的監(jiān)測數據對，若x_ij且y_ij，或x_i>x_j且y_i>y_j，則稱（x_i，y_i）和（x_j，y_j）一致；若x_ij且y_i>y_j，或x_i>x_j且y_ij，則稱（x_i，y_i）和（x_j，y_j）非一致。X、Y兩測點共有C²_n種不同的監(jiān)測數據對，令c表示一致的監(jiān)測數據對，d表示非一致的監(jiān)測數據對，則c+d=C²_n，Kendall系數τ的計算公式如式（11）所示。

1.2.3 Copula函數類型選擇與參數計算

Vine結構確定之后，需要對每棵樹中的每一對隨機變量選擇一個合適的Copula函數，然后利用赤池信息準則（AIC）^［18-19］作為標準進行函數類型選擇，遍歷Gussian、t、Frank、Clayton和Gumbel 5種常用的Copula函數^［20-21］，當AIC值最小時，所對應的Vine-Copula模型即為最優(yōu)模型。

AIC=2K-2lnL（12）

式中：K為參數的數量，對于以上所選5種Copula函數，除t-Copula函數的K為2以外，其余類型函數的K均為1；L為似然函數的最大值，對于R-Vine Copula的聯(lián)合密度函數，其對數似然函數為

式中：N表示樣本數量，θ=（θ₁，θ₂，…，θ_k）表示Vine-Copula模型的參數向量，其余符號含義同式（10）。設θ^為θ的極大似然估計值，則有L（θ^）=max{L（θ）}，根據式（14）的似然方程組，即可求解出模型參數。

1.2.4 模型擬合優(yōu)度檢驗

模型構建后需對其擬合優(yōu)度進行檢驗，常采用K-S（Kolmogorov-Smirnov）檢驗和CvM（Cramér-von Mises）檢驗兩種方法。它們均屬于非參數檢驗，用于判斷樣本與預先給定的分布是否一致，或者兩個樣本的概率分布是否相同。設樣本的經驗累計概率為F_n（x），建模所得到的理論分布累計概率為F（x）。對于n個樣本序列X₁，X₂，…，X_n，對其升序排序為X_（1），X_（2），…，X_（n），k為X_（k）的排列名次，經驗累計概率為F_n（x）可以表達為

式中：k和k+1為樣本次序；n為樣本個數。

假設檢驗的問題：H₀為空間多測點實測值的分布服從所建Vine-Copula模型；H₁為空間多測點實測值的分布不服從所建Vine-Copula模型。

結合式（16）～（17），可得K-S檢驗和CvM檢驗統(tǒng)計量D：

D（n，α）是顯著性水平為α且樣本容量為n時的拒絕臨界值（查表可得），當D>D（n，α），則拒絕H₀，反之則接受H₁。

P為實際的顯著性水平（00.05時，認為所建的大壩變形安全監(jiān)控模型合理。

1.2.5 空間置信域確定

單點監(jiān)控模型預警閾值的設置多采用基于PauTa準則的置信區(qū)間方法，即認為測值的累計概率落入（0，0.13%］和（99.87%，1］區(qū)間是異常的，落入（0.13%，99.87%）區(qū)間則是正常的。為合理確定多測點空間置信域，本文運用蒙特卡洛（Monte Carlo）隨機抽樣法對空間上每個測點測值的累計概率進行隨機抽樣，計算并分析聯(lián)合累計概率的分布，以及統(tǒng)計落入異常域的概率。

選取同一測線的10個測點，利用蒙特卡洛抽樣法分別在10，9，8，…，3，2，1，0個測點異常的情況下對每個測點的累計概率進行隨機抽樣，每組樣本抽取100萬次，并利用已建好的空間Vine-Copula模型計算聯(lián)合累計概率，聯(lián)合累計概率柱狀散點圖見圖3，聯(lián)合累計概率頻率分布見圖4。由圖3～4可知，當所有測點均異常時，樣本聯(lián)合累計概率的頻率均接近0或1。根據統(tǒng)計得知，聯(lián)合累計概率集中在（0，0.001 3］和［0.998 3，1）區(qū)間，再分別統(tǒng)計當異常點個數為9，8，…，3，2，1，0時落入此區(qū)間的頻數。經過計算，（0，0.001 3］和［0.998 3，1）區(qū)間為空間模型異常域，因此置信域為（0.001 3，0.998 3），和PauTa準則基本一致，因此實際應用中可采用PauTa準則設置多測點的空間置信域。

2 工程案例

以SBX高面板堆石壩為例，基于前述變形監(jiān)控模型構建步驟及空間置信域確定方法，提出適宜的SBX高面板堆石壩變形監(jiān)控模型。

2.1 工程概況

此大壩是一座以發(fā)電為主，兼有防洪、航運、梯級補償等綜合效益的Ⅰ等大（1）型工程。主壩變形監(jiān)控內容包括外觀觀測、內觀觀測和面板觀測。對于表面變形，在上游面板、壩頂及下游壩坡的各層馬道布置了6條測線，共計43個測點；對于內部變形，在主壩左0+008.20斷面及主壩右0+071.80斷面的346.00，379.00，404.00 m及445.00 m高程各設置1條內部變形測線，共計布置48支水管式沉降儀和40支引張線式水平位移計；主壩面板設周邊縫、水平縫和垂直縫進行觀測，共計32支測縫計和8支裂縫計。一般而言，大壩同一測線或同一斷面上的測點具有一定關聯(lián)性^［22］。如圖 5所示，SBX主壩壩頂下游側測線（5號測線）上各測點（SA5-1～ SA5-10）變形規(guī)律相似，變化趨勢一致，具有一定的相關性，說明所構建的測線空間模型是合理的。本文以該測線為例，詳細介紹多測點Vine-Copula變形監(jiān)控模型的建模步驟。

2.2 基于測線的空間監(jiān)控模型構建及空間置信域確定

根據1.2節(jié)變形監(jiān)控模型構建流程，構建SBX壩頂5號測線變形監(jiān)控模型，測點布置見圖6。

計算所選取的建模時段為2010年1月至2020年1月，監(jiān)測頻次為每2個月1次，每個測點獲取57個樣本數據。

2.2.1 單測點歷時測值概率分布確定

利用核密度估計法計算各測點測值的概率密度函數，各測點測值的概率密度分布見圖7，累計概率分布見圖8。

2.2.2 Vine-Copula模型結構選擇

（1）Kendall相關系數τ計算。為定量分析測點間的相關性，計算了每兩測點之間的相依性度量指標（Kendall相關系數τ），如圖9所示。可以看出，除邊緣測點SA5-1與其他測點的相關系數相對較低外，其余各測點之間的相關系數都在0.9以上。每對相鄰測點之間的相關系數基本是最大的，說明該測線測點具有“串聯(lián)”的關聯(lián)結構，因此可選用D-Vine-Copula模型建模。

（2）最大生成樹法確定模型結構。測線中10個測點共生成9棵樹，利用最大生成樹（MST）法，使每層結構（Tree）中的Kendall系數τ之和最大。本次分析采用R語言編程，自動對第一棵樹所有連接結構進行遍歷，找到使τ之和最大的結構，確定Tree1結構，再依據Tree1結構進行同樣的遍歷，得到Tree2結構，以此類推。最終確定的Vine結構見圖10。

2.2.3 Copula函數類型選擇與參數計算

利用AIC準則最小原理和極大似然估計法（MLE）確定每層結構中兩兩結點之間的最優(yōu)Copula連接函數類型，并計算其參數，結果見表1。

2.2.4 模型擬合優(yōu)度檢驗

采用K-S檢驗和CvM檢驗對構建的D-Vine-Copula模型進行擬合優(yōu)度檢驗，其P值均接近1，說明模型合理，能較好地擬合測線上各測點之間的聯(lián)合分布，結果見表 2。

2.2.5 空間置信域確定

采用蒙特卡洛隨機抽樣法確定空間監(jiān)控模型置信域。經計算，該測線變形監(jiān)控空間模型的置信域為（0.001 3，0.998 3），因此異常域為（0，0.001 3］和［0.998 3，1）。

3 結 論

（1） 構建了基于多測點實測值的Vine-Copula高土石壩變形監(jiān)控模型，提出了單點歷史測值累計概率計算、Vine結構優(yōu)選、Copula連接函數選擇及其參數計算、模型擬合優(yōu)度檢驗等關鍵步驟的計算方法。

（2） 經蒙特卡洛隨機抽樣法驗證，多測點空間置信域的設置可采用PauTa準則，實際工程中可通過監(jiān)控多測點聯(lián)合分布函數，來實現(xiàn)對大壩同一測線或斷面整體變形特性的監(jiān)控。

（3） SBX高面板堆石壩工程應用表明，Vine-Copula變形監(jiān)控模型能合理考慮多測點時序特性和空間關聯(lián)性，其K-S檢驗和CvM檢驗的P值均大于0.9，模型的合理性和精度均較高，能較好地實現(xiàn)大壩整體變形特性的實時監(jiān)控。

參考文獻：

［1］李智錄.大壩安全監(jiān)控統(tǒng)計模型研究［D］.西安：西安理工大學，2006.

［2］WEI B，YUAN D，XU Z，et al.Modified hybrid forecast model considering chaotic residual errors for dam deformation［J］.Structural Control and Health Monitoring，2018，25（8）：1-16.

［3］裴亮，吳震宇，崔萌，等.高土石壩安全監(jiān)測位移混合模型研究及應用［J］.四川大學學報（工程科學版），2012，44（增1）：42-47.

［4］林智艷.基于BP神經網絡的土石壩變形預測模型研究［J］.人民珠江，2020，41（6）：74-78.

［5］郭芝韻，李丹，劉炳銳.基于改進ABC-BP的大壩變形監(jiān)控模型研究［J］.人民長江，2016，47（6）：1001-4179.

［6］張柯，楊杰，程琳.基于ABC-SVM的土石壩變形監(jiān)測模型［J］.水資源與水工程學報，2017，28（4）：199-204.

［7］萬凱.基于支持向量機的土石壩安全監(jiān)測數據分析及其應用研究［D］.南昌：南昌大學，2020.

［8］任秋兵，李明超，沈揚，等.耦合時空相關特性的大壩變形動態(tài)監(jiān)控模型［J］.水力發(fā)電學報，2021，40（10）：160-172.

［9］蔡忍，黃耀英，萬智勇，等.基于投影尋蹤-云模型法的碾壓混凝土壩綜合變形監(jiān)控指標擬定［J］.武漢大學學報（工學版），2019，52（3）：194-200.

［10］王少偉，包騰飛，胡坤.基于PCA的高混凝土壩變形空間融合監(jiān)控模型［J］.水利水電技術，2018，49（8）：123-127.

［11］劉章君，郭生練，許新發(fā)，等.Copula函數在水文水資源中的研究進展與述評［J］.水科學進展，2021，32（1）：148-159.

［12］何敏園，李紅權.全球股市間的相依結構與極值風險溢出：基于藤Copula的金融復雜性分析［J］.管理評論，2020，32（7）：102-110.

［13］于文華，楊坤，魏宇.基于高頻波動率模型與R-Vine Copula的行業(yè)資產組合風險測度研究［J］.運籌與管理，2021，30（6）：132-138.

［14］SKLAR M.Fonctions de répartition én dimensions et leurs marges［J］.Annales de I′ISUP，1959，8（3）：229-231.

［15］AAS K，CZADO C，F(xiàn)RIGESSI A.Pair-copula constructions of multiple dependence［J］.Mathematics and Economics，2009，44（2）：182-198.

［16］BEDFORD T，COOKE R M.Vines：a new graphical model for dependent random variables［J］.The Annals of Statistics，2002，30（4）：1031-1068.

［17］CZADO C.Analyzing dependent data with vine copulas：a practical guide with R［M］.Switzerland：Springer，2019.

［18］GENEST C，MACKAY J.The joy of copulas：bivariate distributions with uniform marginals［J］.The American Statistician，1986，40（4）：280-283.

［19］FANG K T，KOTZ S，NG K W.Symmetric multivariate and related distributions［M］.Virginia：Chapman & Hall，2018.

［20］SHIH J H，LOUIS T A.Inferences on the association parameter in copula models for bivariate survival data［J］.Biometrics，1995，42：1384-1399.

［21］AKAIKE H.A new look at the statistical model identification［J］.IEEE Transactions on Automatic Control，1974，19（6）：716-723.

［22］WANG S，XU Y，GU C，et al.Two spatial association-considered mathematical models for diagnosing the long-term balanced relationship and short-term fluctuation of the deformation behaviour of high concrete arch dams［J］.Structural Health Monitoring，2020，19（5）：1421-1439.

（編輯：胡旭東）

Research on deformation monitoring model for high earth-rock dams based on Vine-Copula

CHEN Tianci^1，2，LI Yanling^1，2，ZHANG Fang³，CHEN Xiao⁴

（1.State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China；2.College of Water Resources and Hydropower，Sichuan University，Chengdu 610065，China；2.Power China Guiyang Engineering Corporation Limited，Chengdu 610065，China；3.Zhenxiong County Water Bureau，Zhaotong 657200，China）

Abstract：Aiming at the problem that the deformation monitoring model for high earth-rock dams is mainly based on a single measuring point and cannot quantitatively consider the spatial correlation of measuring points，a deformation monitoring model based on Vine-Copula was constructed，and a spatial confidence domain early warning threshold setting method based on Monte-Carlo random sampling method was proposed.In the process of the model construction，the time series characteristics and spatial correlation between multiple measuring points were fully considered，and the Vine-Copula method was used to accurately model and analyze the deformation data to reveal the overall trend of high earth-rock dam deformation.At the same time，the spatial confidence region was determined by Monte-Carlo random sampling method，which provided a scientific basis for the setting of early warning threshold.The engineering practice showed that the model simulation results can accurately reflect the overall deformation trend of high earth-rock dam，with high accuracy and rationality，and effectively realize the expansion of monitoring effect-quantity to the whole space of high earth-rock dams.The research results can provide new ideas and methods for the safety monitoring of high earth-rock dams，and have important theoretical significances and practical values.

Key words：high earth-rock dam；deformation monitoring model；Vine structure；Copula function；spatial confidence domain