基于接觸單元的穿越施工管線變形數值模擬方法

摘要 新建盾構隧道穿越施工將引起既有地下管線產生變形,在采用數值模擬方法進行管線變形計算時可采用接觸單元模擬管土相互作用,但現有方法未對接觸單元計算參數的選取進行討論,不能保證計算結果的可靠性。文章采用有限元軟件Ansys對新建盾構隧道穿越既有地下管線的數值模擬方法進行了研究,其中,管線與土體的相互作用通過接觸單元進行模擬。為選擇合適的接觸單元計算參數,對管線與土體復雜的接觸問題進行了力學簡化,分析了有限元軟件中接觸剛度與工程中常見力學參數的聯系,給出了接觸剛度的試算過程及其他接觸單元計算參數的選取依據。將管線變形和彎矩計算結果與既有文獻中理論計算結果及離心模型試驗數據進行了對比,并選取實際工程進行了案例計算。
關鍵詞 數值模擬;接觸單元;盾構隧道;地下管線;管土相互作用
中圖分類號 U455文獻標識碼 A文章編號 2096-8949(2024)08-0001-04
0 引言
隧道開挖引起的管線變形問題為管線與土層的相互作用問題,數值模擬能夠較為真實地反映管土相互作用,且能直觀地模擬隧道開挖與支護的過程,相較于模型試驗又具有成本較低的優點,在學術界及工程界得到大量應用[1-5]。
目前管土相互作用的有限元模擬方法主要包含三種類型:一類是地基彈簧,其中彈簧一端與管線單元共用節點,另一端施加土體位移荷載;一類是采用Abaqus中的管土相互作用單元,需土體位移荷載作為模型的輸入數據;最后一類為接觸單元,能夠較為全面地模擬管線與土體之間法向、切向的相對運動與力學行為。根據現有的大多數研究報道可知,在使用接觸單元模擬管土相互作用時,一般采用軟件默認的接觸單元計算參數,并未對接觸單元的參數選取進行討論,也未實現接觸單元計算參數與常用管土相互作用參數的對應。
該文采用接觸單元模擬管土相互作用,建立了隧道穿越既有管線的有限元模型。為選擇合適的接觸單元計算參數,通過研究地基系數與接觸剛度的關系,給出了接觸剛度的試算過程,并詳細介紹了其他接觸單元計算參數的選取依據。依托實際工程施工參數進行了案例計算,對該文方法的正確性進行了驗證。
1 模型建立
1.1 模型假設
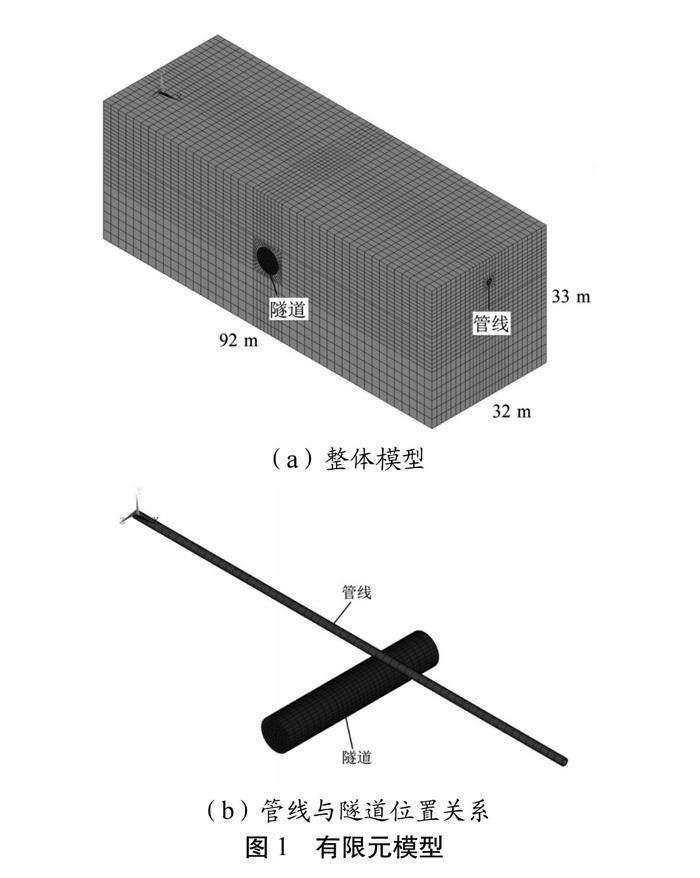
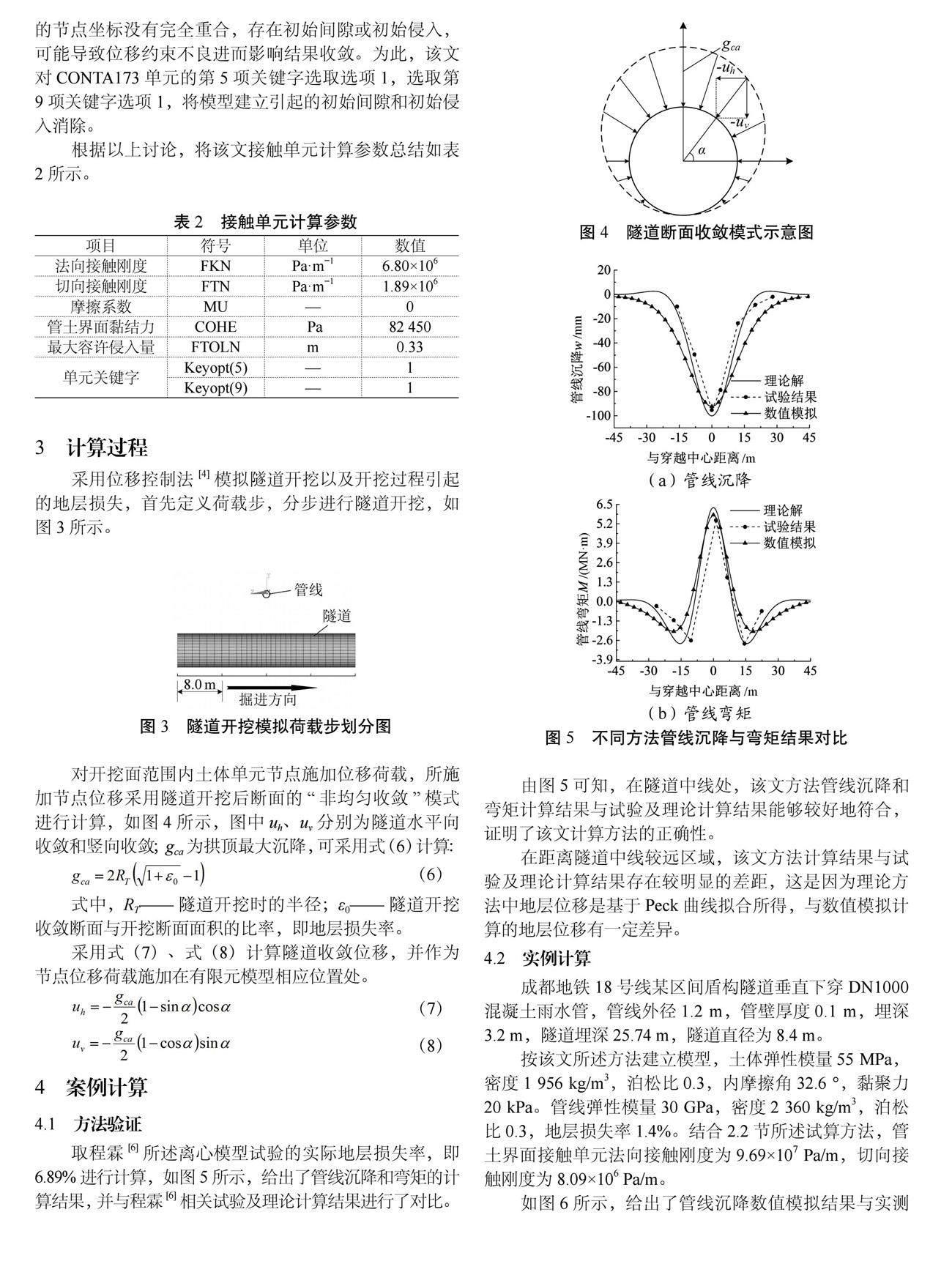
采用Ansys軟件建立隧道穿越既有管線模型,有限元模型尺寸參考程霖[6]所述離心模型試驗原型尺寸(92 m×32 m×33 m)。如圖1所示。
土體和管線均采用實體單元SOLID185進行網格劃分,管土界面相互作用采用接觸單元CONTA173和目標單元TARGE170建立接觸進行模擬。
1.2 接觸單元的生成規則
接觸面與目標面通過摩擦傳遞切線作用力,通過“侵入”傳遞法向作用力,且接觸面不能侵入目標面,而反之則可以,故而可選較硬的面作為目標面,較軟的面作為接觸面。根據管線與土體的材料性質,將土體內表面作為接觸面,建立接觸單元CONTA173,管線外表面作為目標面,建立目標單元TARGE170。Ansys軟件通過識別相同編號的實常數,自動識別目標單元與接觸單元并建立接觸對。
2 計算參數
2.1 土體和管線參數
該文采用EDP模型進行土體材料模擬,EDP模型包含2個計算參數,分別是屈服參數σye和壓力敏感參數αp,可通過土體內摩擦角φ和內黏聚力c進行推導,即:
(1)
(2)
EDP模型流動法則計算參數參照式(1)進行推導,但需要用剪脹角ψ代替內摩擦角φ。該文剪脹角取值為內摩擦角的1/2,按非關聯流動法則進行計算[7]。土體和管線的計算參數見表1。
2.2 接觸單元參數
對于該文所研究的管線與土體相互作用問題,管土法向接觸剛度、切向接觸剛度、法向容許侵入量、管土界面黏結力、管土摩擦系數為關鍵計算參數,關系到管線變形與受力計算的準確性。
2.2.1 接觸剛度
在Ansys中,接觸剛度包含法向接觸剛度(FKN)與切向接觸剛度(FKT),其與地基系數量綱一致(FL-3),但由于力學原理不同,兩者有不同的取值,下面給出通過地基系數確定接觸剛度的簡便試算方法。
計算簡圖如圖2所示,當管土產生相對位移時,假設管線截面形狀不發生改變,對于管線與土體豎向相對運動,假設管線在荷載作用下橫截面不發生形變。圖2(a)為管土發生相對位移后,管線的受力情況,其中,α為任意圓心角,δv為管土豎向相對位移,pn、pf為管線受到的法向荷載和切向荷載,D為管線外徑。圖2(b)為有限元計算過程中管線(目標面)與土體(接觸面)相互侵入示意圖,在有限元模型中,管土相互侵入量小于管線位移,將最大侵入量與管線豎向位移的比值記為參數ζ。
根據圖2的幾何關系,令接觸單元FKN和FKT分別為fN和fT,則管線所受地基反力可表示為:
(3)
式中,α0=arcsin(ζδv/D);δh——管土相對切向位移。
根據Winkler地基模型,管線所受地基反力還可表示為:
PR=KvDδv (4)
式中,Kv——基于Winkler地基模型的地基系數。
比較式(3)和式(4),可得:
(5)
根據式(5),結合室內加載試驗對接觸剛度進行試算,試算步驟:
(1)按室內加載試驗測得地基系數(包括豎向與切向)定義有限元軟件中FKN和FKT初始值。
(2)對圖1管線模型施加室內加載試驗所得管線極限位移,計算得到的管線所受豎向地基反力及接觸單元最大侵入量,通過最大侵入量與管線豎向位移的比值計算參數ζ。
(3)根據式(5)調整FKN取值,并反復進行有限元計算,使計算所得管線豎向地基反力與加載試驗測得的極限荷載一致;FKN取值確定后,采用以上思路對FKT進行試算。
2.2.2 最大容許侵入量
在Ansys中最大容許侵入量采用參數FTOLN表示,取值分為正值與負值:取正值時FTOLN為比例系數,默認值為0.1;取負值時FTOLN的絕對值為最大容許侵入量的實際數值。該文計算模型取FTOLN為室內加載試驗測得管線豎向極限位移。
2.2.3 摩擦系數和管土界面黏結力
在Ansys中,接觸單元界面黏結力和摩擦系數分別用COHE和MU表示。接觸單元的切向摩擦符合庫倫模型,當摩擦力超過庫倫模型規定的等效剪應力時,接觸界面發生相對滑動。該文計算模型令管土摩擦系數為0,取室內試驗[6]測得的管土切向極限荷載作為管土界面黏結力。
2.2.4 單元關鍵字
有限元模型劃分網格單元后,目標單元與接觸單元的節點坐標沒有完全重合,存在初始間隙或初始侵入,可能導致位移約束不良進而影響結果收斂。為此,該文對CONTA173單元的第5項關鍵字選取選項1,選取第9項關鍵字選項1,將模型建立引起的初始間隙和初始侵入消除。
根據以上討論,將該文接觸單元計算參數總結如表2所示。
3 計算過程
采用位移控制法[4]模擬隧道開挖以及開挖過程引起的地層損失,首先定義荷載步,分步進行隧道開挖,如圖3所示。
對開挖面范圍內土體單元節點施加位移荷載,所施加節點位移采用隧道開挖后斷面的“非均勻收斂”模式進行計算,如圖4所示,圖中uh、uv分別為隧道水平向收斂和豎向收斂;gca為拱頂最大沉降,可采用式(6)計算:
(6)
式中,RT——隧道開挖時的半徑;ε0——隧道開挖收斂斷面與開挖斷面面積的比率,即地層損失率。
采用式(7)、式(8)計算隧道收斂位移,并作為節點位移荷載施加在有限元模型相應位置處。
(7)
(8)
4 案例計算
4.1 方法驗證
取程霖[6]所述離心模型試驗的實際地層損失率,即6.89%進行計算,如圖5所示,給出了管線沉降和彎矩的計算結果,并與程霖[6]相關試驗及理論計算結果進行了對比。
由圖5可知,在隧道中線處,該文方法管線沉降和彎矩計算結果與試驗及理論計算結果能夠較好地符合,證明了該文計算方法的正確性。
在距離隧道中線較遠區域,該文方法計算結果與試驗及理論計算結果存在較明顯的差距,這是因為理論方法中地層位移是基于Peck曲線擬合所得,與數值模擬計算的地層位移有一定差異。
4.2 實例計算
成都地鐵18號線某區間盾構隧道垂直下穿DN1000混凝土雨水管,管線外徑1.2 m,管壁厚度0.1 m,埋深3.2 m,隧道埋深25.74 m,隧道直徑為8.4 m。
按該文所述方法建立模型,土體彈性模量55 MPa,密度1 956 kg/m3,泊松比0.3,內摩擦角32.6 °,黏聚力20 kPa。管線彈性模量30 GPa,密度2 360 kg/m3,泊松比0.3,地層損失率1.4%。結合2.2節所述試算方法,管土界面接觸單元法向接觸剛度為9.69×107 Pa/m,切向接觸剛度為8.09×106 Pa/m。
如圖6所示,給出了管線沉降數值模擬結果與實測數據的對比。可見,管線變形計算值與實測值較為符合。
圖6 實測數據與數值模擬結果的對比
5 結論
該文采用Ansys軟件建立了隧道穿越既有管線有限元模型,使用接觸單元模擬管土相互作用。通過簡化管線與土體相互作用力學模型,建立了接觸剛度與工程實際參數中豎向地基系數與切向地基系數的關系,給出了接觸剛度的試算方法。詳細介紹了接觸單元最大容許侵入量、摩擦系數、黏結強度、單元關鍵字等參數的含義及取值依據。給出了基于控制位移法和單元“生死”技術的盾構隧道開挖模擬方法。
將數值模擬計算結果與既有程霖[6]離心模型試驗測得數據和理論方法計算結果進行了對比,在隧道開挖中線附近,數值模擬方法所得管線變形和彎矩與理論解和試驗數據相符,選取實際工點進行案例計算,管線變形計算值與實測值較為符合,證明了該文建模方法的正確性。
參考文獻
[1]KLAR A, MARSHALL A M. Shell versus beam representation of pipes in the evaluation of tunneling effects
on pipelines[J]. Tunnelling and Underground Space Technology, 2008(4): 431-437.
[2]WANG Y, SHI J W, NG C W W. Numerical modeling of
tunneling effect on buried pipelines[J]. Canadian Geotechnical Journal, 2011(7): 1125-1137.
[3]王霆, 羅富榮, 劉維寧, 等. 地鐵車站洞樁法施工引起的地表沉降和鄰近柔性接頭管道變形研究[J]. 土木工程學報, 2012(2): 155-161.
[4]邵羽. 盾構雙隧道施工對臨近地埋管線的影響研究[D]. 南寧:廣西大學, 2017.
[5]SHAO Y, DUAN Z B, LIU Y, et al. Estimating the effects of tunnelling on preexisting jointed pipelines[J]. Advances in Civil Engineering, 2019(4): 1-12.
[6]程霖. 地鐵隧道開挖引起地下管線變形的理論分析和試驗研究[D]. 北京:北京交通大學, 2021.
[7]孔位學, 芮勇勤, 董寶弟. 巖土材料在非關聯流動法則下剪脹角選取探討[J]. 巖土力學, 2009(11): 3278-3282.

