地鐵連續剛構橋上無砟軌道無縫線路縱向力分析

張鵬飛 江浩宇 胡達貴

摘要：【目的】為研究地鐵連續剛構橋上無砟軌道無縫線路縱向受力與變形規律，對地鐵連續剛構橋上無砟軌道無縫線路設計改進、運營養護維修提供理論指導。【方法】根據梁-板-軌相互作用原理，建立地鐵連續剛構橋上整體道床式無砟軌道無縫線路空間耦合模型，計算伸縮、撓曲、制動、斷軌工況下軌道結構和橋梁縱向力及位移，并對軌道結構靜力特性進行對比分析，為地鐵連續剛構橋上無縫線路軌道結構設計提供參考。【結果】結果表明：雙線列車荷載中點與中部梁端處重合時為列車垂向荷載最不利工況，此時鋼軌縱向力與鋼軌、橋梁縱向位移均為最大，均出現在中部梁端附近，數值分別為70.3 kN與0.6，0.8 mm；雙線制動荷載列車尾部位于兩側梁端時為列車制動荷載最不利工況，此時鋼軌縱向力與鋼軌、橋梁縱向位移均為最大，數值分別為107.8 kN與1.6，1.7 mm。【結論】伸縮力作用下各個端部橋縫處為薄弱部位，在平時養護中應特別注意梁端部橋縫處軌道結構，防止因伸縮力過大而產生斷軌；鋼軌發生斷軌時，在斷縫處縱向力、縱向位移均發生突變，嚴重影響線路行車安全。

關鍵詞：地鐵連續剛構橋；整體道床；橋上無縫線路；縱向力

中圖分類號：U213.9 文獻標志碼：A

文章編號：1005-0523（2024）02-0064-08

Longitudinal Force Analysis of Ballastless Track Continuous

Welded Rail on Subway Continuous Rigid Frame Bridge

Zhang Pengfei， Jiang Haoyu， Hu Dagui

（State Key Laboratory of Performance Monitoring Protecting of Rail Transit Infrastructure， East China Jiaotong

University，Nanchang 330013， China）

Abstract： 【Objective】In order to study the longitudinal force and deformation law of CWR of ballastless track on the continuous rigid bridge of the metro，and to provide theoretical guidance for the design improvement， operation and maintenance. 【Method】Based on the principle of beam-plate-rail interaction， a spatial fine coupling model of CWR of the integral track bed type ballastless track on the continuous rigid bridge of the metro was established，and under stretching， bending，braking and broken rail conditions， the displacementtrack and longitudinal force of track structure and bridge were calculated， and the static characteristics of the track structure were compared and analyzed. This paper provides a reference for the design of CWR track structure on continuous rigid bridge of metro. 【Result】The results show that when the midpoint of the double-line train load coincides with the end of the middle beam， the vertical load of the train is the most unfavorable working condition， and the force of the rail and the displacement of the rail and bridge are the largest， and the values are 70.3 kN， 0.6 mm and 0.8 mm， respectively. When the tail of the double-line brake load train is located at the end of the beams on both sides， the most unfavorable working condition of the train braking load， at this time，the longitudinal force of the rail and the longitudinal displacement of the rail and the bridge are the largest， and the values are 107.8 kN，1.6 mm and 1.7 mm， respectively. 【Conclusion】Under expansion force， each end bridge joint is a weak part， and attention should be paid to the structure at the end bridge joint of the beam in the usual maintenance to prevent rail breakage due to excessive expansion force; When the rail is broken under cooling conditions， the longitudinal force and longitudinal displacement of the broken rail are abruptly changed at the fracture， which seriously affects the safety of the line.

Key words： metro continuous rigid bridge; integral track bed; continuous welded rail on the bridge; longitudinal force

Citation format： ZHANG P F， JIANG H Y， HU D G. Longitudinal force analysis of ballastless track continuous welded rail on subway continuous rigid frame bridge[J]. Journal of East China Jiaotong University， 2024， 41（2）： 64-71.

【研究意義】地鐵高架線路相對地下線路具有造價低、施工速度快、適應能力強等優點，連續剛構橋上無砟軌道無縫線路因具有高平順性及穩定性，在地鐵高架線路中應用逐漸增多。探索地鐵高架線路連續剛構橋上無砟軌道無縫線路縱向力的分布規律和影響因素，為優化無砟軌道結構參數和提高線路平順性提供理論支持。

【研究進展】國內外學者在橋上無砟軌道領域進行了大量研究工作，張鵬飛等[1]建立了剛構橋上CRTSⅠ型雙塊式與CRTSⅢ型板式無砟軌道模型，并對兩種軌道結構靜力特性進行了對比分析；陳鵬等[2]分析了改變支座位置、跨長、聯數等因素影響下，橋上無縫線路力學特征與變化規律；宋曉宇等[3]探討了工字型鋼連續組合梁剛性節點的傳力機制；倪向陽等[4]分析了改變橋梁結構條件下，橋上無縫線路軌道結構受力變化規律；王平等[5-8]建立了連續剛構橋上無縫線路模型，研究了伸縮附加力的放散計算；吳亮秦等[9]通過列車制動試驗，探究了制動條件下橋梁受力及其傳遞規律；程杰[10]分析了橋墩橫向剛度對無支座預應力混凝土連續剛構橋的影響規律；Ma等[11]建立了橋梁模型，提出可能影響撓度的因素，采用控制單個因素值的靈敏度分析方法得到撓度計算結果；Yan[12]研究了支承基礎發生不均勻沉降時，連續剛構橋力學特性的變化規律；Li等[13]通過對頂部合龍相對位移的比較分析，確定了剛構橋高墩優化計算模型；朱志輝等[14]采用點荷載模式分析了列車荷載作用下的無縫線路附加力；羅華朋等[15]建立高墩大跨橋墩，分析了橋墩在太陽輻射下形成溫差時，橋墩剛度對無縫線路附加力的影響規律；王偉華[16]建立了多聯連續剛構橋上無縫線路模型，研究了不同剛度對附加力的影響；。

【創新特色】綜上，目前針對連續剛構橋上無砟軌道無縫線路的研究較少，且較少考慮軌道結構之間的相互作用。為探究地鐵連續剛構橋上無砟軌道無縫線路縱向受力與變形規律，對地鐵連續剛構橋上無砟軌道無縫線路設計改進、運營養護維修提供理論指導。【關鍵問題】針對地鐵連續剛構橋上無縫線路結構特點，建立空間精細化耦合模型，分析伸縮力、撓曲力、制動力和斷軌力作用下地鐵連續剛構橋上無縫線路縱向力分布規律，研究成果以期為地鐵連續剛構橋上無縫線路設計優化提供參考。

1 精細化空間有限元建模

1.1 模型概述

地鐵連續剛構橋上無砟軌道無縫線路包括鋼軌、扣件、整體道床、變截面梁體、墩梁固結等細部結構，建模時均需詳細考慮。本文根據梁-板-軌相互作用原理，利用有限元分析軟件結合考慮實際力學屬性，建立100 m路基+4×40 m連續剛構橋+4×40 m連續剛構橋+100 m路基的地鐵連續剛構橋上無縫線路模型，橋梁的布置簡圖見圖1，兩側陰影部分為路基段。

1.2 模型參數

鋼軌為細長結構且要發生彎曲、扭轉、伸縮等變形，而梁單元可以承受拉、壓、扭轉和彎曲等荷載，故CHN60鋼軌選用BEAM188梁單元。

鋼軌和軌枕間有扣件約束，采用COMBIN14線性彈簧單元模擬扣件的橫向和垂向剛度，其大小分別為50，35 kN/mm；扣件縱向阻力采用COMBIN39非線性彈簧單元進行模擬。全橋鋪設WJ-2A型小阻力扣件，高架線地段扣件節點間距取590 mm，單組扣件最大縱向阻力取7 kN/組。

高架線地段道床分塊布置，設置橫向縫，縫寬一般為100 mm，梁縫處道床橫向縫寬為150 mm。路基地段道床設置和橋梁地段相同。整體道床混凝土強度C40，變截面橋梁梁體按圖紙尺寸建模，采用C60混凝土，二者均選用SOLID45實體單元。墩頂縱向剛度選用COMBIN14彈簧單元，剛度根據工程資料取1 244 kN/cm進行計算分析。地鐵連續剛構橋1/2截面見圖2，鋼軌編號見圖3，詳細結構參數見表1。

1.3 模型驗證

建立同王平等[7]研究成果中相似的無縫線路模型進行附加縱向力的計算，并與之進行比對。模型除橋梁截面與跨度外其他計算參數均采用與文獻相同的數值。計算結果見圖4。

由圖4結果對比可知，本文鋼軌縱向力計算結果的分布規律變化趨勢基本同王平等[7]計算結果一致，考慮到本文中剛構橋截面尺寸和跨度與文獻存在差異，因此可以認為所建立的有限元模型是準確可行的。

2 模型加載

1） 分析伸縮力時，為對比不同溫差荷載下伸縮力的差異，對剛構橋梁體與整體道床施加溫度荷載。

2） 分析撓曲力時，列車長度120 m，車輪軸重為14 t，采用設計荷載，等效為均布荷載，荷載長度120 m、大小為28 kN/（m?線）［17］。

3） 分析制動力時，輪軌黏著系數采用0.25。制動荷載以均布荷載形式進行施加，荷載作用位置為鋼軌頂面，大小為7 kN/m，長度為120 m。

4） 分析斷縫值時，梁體降溫30 ℃，道床降溫35 ℃，鋼軌降溫60 ℃。斷軌位置取剛構橋左端與路基連接處。

3 無縫線路縱向力計算分析

圖3～圖13與表3～表8中，縱向力正值為拉力，負值為壓力。

3.1 伸縮力計算結果分析

對剛構橋梁體與整體道床施加不同溫度荷載，具體工況見表2。

溫度荷載作用下，剛構橋上鋼軌縱向力及鋼軌、橋梁縱向位移見圖3～圖5。結構縱向力及位移最大值見表3。

由圖5～圖7與表3可知，隨著溫升的增大，軌道結構受力與變形均增大。鋼軌縱向力最大值均出現在橋梁端部，鋼軌位移最大值出現在橋梁內側靠近中間端部的位置，橋梁位移最大值出現在橋梁端部。

工況3各項數值均為3種工況最大，鋼軌伸縮力最大值出現在兩跨橋梁相連端部，表現為壓力，大小為445.9 kN。鋼軌縱向伸縮位移最大值出現在路基與橋梁相連端部附近，表現為拉伸位移，大小為8.1 mm。橋梁縱向伸縮位移最大值出現在與路基連接端部，數值均為23.8 mm，左側表現為壓力，右側表現為拉力。工況2及工況3相比各自前一工況，鋼軌最大縱向力分別增加了22.2%，6.0%，鋼軌及橋梁最大縱向位移分別增加了50.0%，17.4%與91.7%，47.8%。

綜上所述，在計算地鐵連續剛構橋無砟軌道無縫線路伸縮力時，需考慮不同軌道結構的溫度差異對受力與變形產生的影響。隨著溫度的上升，各個結構對溫度的敏感度逐漸下降。此外各個端部橋縫處為薄弱部位，在平時養護中應特別注意梁端部橋縫處軌道結構，防止因伸縮力過大而產生斷軌。

3.2 撓曲力計算結果分析

模擬列車雙線對向駛入橋梁，施加120 m垂向均布荷載進行撓曲力計算，工況見表4。

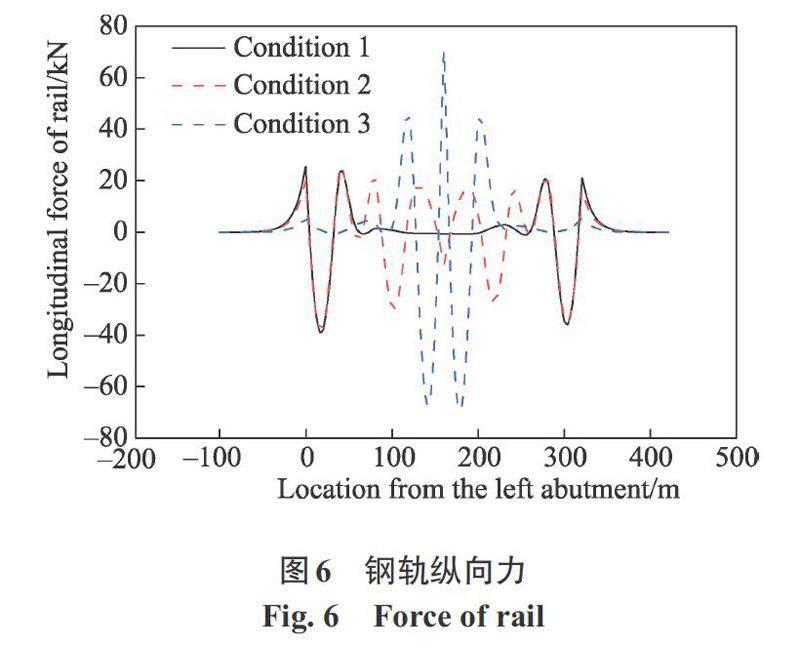
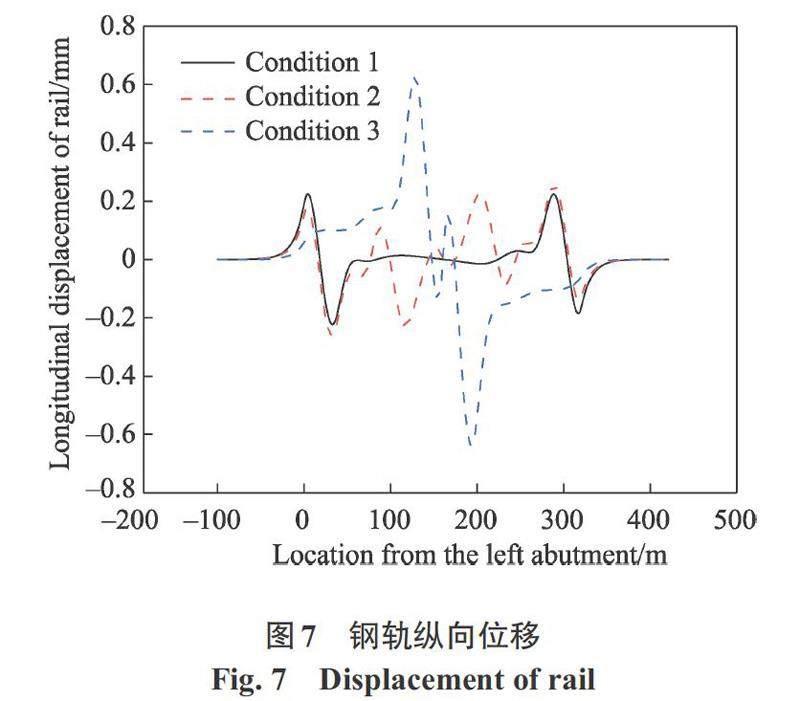
由于工況均為雙線加載且荷載對稱，選取1號鋼軌為研究對象。計算結果見圖6～圖8，雙線加載撓曲工況鋼軌縱向力與鋼軌、橋梁縱向位移最值見表5。由圖6～圖8與表5可知，不同加載工況最大撓曲力及最大結構位移產生的位置不同，但3種工況中鋼軌撓曲力、鋼軌及橋梁位移均在有車輛荷載作用的橋梁端部產生最大值，在車頭車尾處產生峰值，且在遠離荷載位置逐漸減小，即兩輛列車交會于中部梁端時相互影響作用最大。

在雙線加載撓曲工況下，工況3的鋼軌縱向力與鋼軌、橋梁縱向位移均為最大，均出現在中部梁端附近，數值分別為70.3，69.3 kN與0.6，0.8 mm。可知在雙線列車逐漸駛入橋梁中部時撓曲力及各項結構位移逐漸增大，且在交匯處相互作用最大。

綜上所述，地鐵連續剛構橋上無砟軌道無縫線路受列車垂向荷載時，需關注梁縫處軌道結構的受力與變形。列車荷載作用于中部梁端處作用力明顯大于兩側梁端處，并在車頭車尾產生峰值。在計算列車荷載下地鐵連續剛構橋上無砟軌道無縫線路軌道受力和變形時，荷載中點與中部梁端處重合時（即工況3）為綜合最不利工況。

3.3 制動力計算結果分析

模擬列車雙線對向駛入橋梁，施加120 m均布荷載進行制動力計算，工況見表6。

由于工況均為雙線加載且荷載對稱，選取一根鋼軌為研究對象。計算結果見圖9～圖11。雙線加載撓曲工況鋼軌縱向力與鋼軌、橋梁縱向位移見表7。由圖9～圖11與表7可知，在雙線加載制動工況下，工況2的鋼軌縱向力與鋼軌、橋梁縱向位移均為最大，數值分別為107.8 kN與1.6，1.7 mm。工況3產生的縱向力與位移最小，且橋梁位移趨近于零。工況2及工況3相比各自前一工況，鋼軌最大縱向力分別增大了121.5%，-57.9%，鋼軌及橋梁最大縱向位移分別增大了166.7%，-100%與188.3%，-100%。可知在列車逐漸駛入橋梁中部時制動力及各項結構呈先增大后減小趨勢，且近距離對向制動會產生較大抵消作用。

綜上所述，在計算地鐵連續剛構橋上無砟軌道無縫線路制動力時，列車頭尾位于梁端時產生的作用力明顯大于列車中部位于梁端產生的作用力。在計算地鐵連續剛構橋上無砟軌道無縫線路受到制動荷載產生的受力和變形時，列車頭尾位于梁端時為綜合最不利工況（即工況2），需著重注意端部軌道結構的日常保養及維護、檢測。

3.4 斷軌力計算結果分析

鋼軌折斷條件下，鋼軌斷軌力及鋼軌位移計算結果見圖12～圖13，斷軌工況鋼軌斷軌力與縱向位移最值見表8。

由圖12～圖13與表8可知，在鋼軌折斷處，斷軌縱向力趨近于零；而在梁端處，未折斷鋼軌縱向力達到最大值；折斷鋼軌形成的斷縫值為73.1 mm；斷軌與非斷軌力最大值分別為1566.8，1 568.7 kN，最小值分別為0，739.6 kN。

綜上所述，鋼軌發生斷軌時，斷軌對鋼軌產生瞬時的影響，并會影響其他線路，發現斷軌應及時更換鋼軌，避免發生危險。

4 結論

1） 溫度荷載作用下，隨著溫度的上升，各個結構對溫度的敏感度逐漸下降。鋼軌縱向力在梁端表現為壓力、在跨中表現為拉力；橋梁各個端部為無縫線路的薄弱環節，中間端部的縱向力大于橋梁與路基連接處端部縱向力。

2） 列車垂向荷載作用下，列車荷載作用于中部梁端處時，作用力明顯大于兩側梁端處，并在車頭車尾產生峰值。列車垂向荷載往中部移動時產生的撓曲力逐漸加大，在列車荷載中部與橋梁中部梁端重合時產生最大值。雙線列車荷載中點與中部梁端處重合時為列車垂向荷載最不利工況。

3） 列車制動荷載作用下，縱向位移在橋梁各個端部及荷載首尾端產生峰值。在列車從橋頭逐漸駛入橋梁中部時制動力及各項結構位移呈先增大后減小趨勢。雙線加載時與撓曲工況會疊加不同，制動工況在對向加載時會產生抵消作用，可減少鋼軌受力及結構位移。雙線制動荷載列車尾部位于兩側梁端時為列車制動荷載最不利工況。

4） 鋼軌在低溫條件下折斷，斷縫處鋼軌縱向力發生突變，非折斷鋼軌在斷縫同一橫坐標表現為拉力；折斷鋼軌在斷口處急劇收縮，使得鋼軌縱向位移在此處發生較大變化，并對梁端產生斷軌力。

參考文獻：

[1]? ?張鵬飛， 黃安琪， 胡達貴， 等. 剛構橋上無砟軌道無縫線路靜力特性分析[J]. 華東交通大學學報， 2023， 40（2）： 30-38.

ZHANG P F， HUANG A Q， HU D G， et al. Comparative analysis on static characteristics of CWR of ballastless track on rigid frame bridge[J]. Journal of East China Jiaotong University， 2023， 40（2）： 30-38.

[2]? ?陳鵬， 高亮， 馮雅薇， 等. 連續梁橋上無縫線路縱向附加力的變化規律[J]. 北京交通大學學報， 2007， 31（1）： 85-88.

CHEN P， GAO L， FENG Y W， et al. Variety rules of additional longitudinal force of continuously welded rails on bridge with continuous beam[J]. Journal of Beijing Jiaotong University， 2007， 31（1）： 85-88.

[3]? ?宋曉宇， 白玲. 鐵路連續復合剛構橋墩梁剛性節點的受力分析[J]. 北京交通大學學報， 2011， 35（3）： 77-80.

SONG X Y， BAI L. Mechanical characteristics analysis of pier-girder rigid node of continuous hybrid rigid frame railway bridge[J]. Journal of Beijing Jiaotong? University， 2011， 35（3）： 77-80.

[4]? ?倪向陽. 城市軌道交通橋上無縫線路撓曲力研究[D]. 北京： 北京交通大學， 2012.

NI X Y. The study of deflection force in CWR of urban rail transit[D]. Beijing： Beijing Jiaotong University， 2012.

[5]? ?謝鎧澤， 徐井芒， 王平， 等. 橋上無縫線路附加伸縮力放散的計算研究[J]. 鐵道標準設計， 2012（4）： 28-31.

XIE K Z， XU J M， WANG P， et al. Research on the calculation of stress relief of additional expansion force of continuously welded rails on bridge[J]. Railway Standard Design， 2012（4）： 28-31.

[6]? ?謝鎧澤， 王平， 徐浩， 等. 剛構橋上無砟軌道無縫線路病害研究[J]. 中南大學學報（自然科學版）， 2014， 45（6）： 2085-2091.

XIE K Z， WANG P， XU H， et al. Diseases of continuous welded rail of ballstless track on rigid frame bridge[J]. Journal of Central South University （Science and Technology）， 2014， 45（6）： 2085-2091.

[7]? ?王平， 謝鎧澤. 連續剛構橋上無縫線路計算模型及方法的簡化[J]. 中南大學學報（自然科學版）， 2015， 46（7）： 2795-2743.

WANG P， XIE K Z. Simplification for calculation model and method of CWR on continuous rigid frame bridge[J]. Journal of Central South University （Science and Technology）， 2015， 46（7）： 2795-2743.

[8]? ?熊震威， 謝鎧澤， 王平， 等. 列車制動對剛構橋上無縫線路梁軌相對位移的影響研究[J]. 鐵道標準設計， 2013， 57（10）： 10-14.

XIONG Z W， XIE K Z， WANG P， et al. Influence of train braking on relative displacement between girder and rail of continuous welded rail upon rigid-frame bridge[J]. Railway Standard Design， 2013， 57（10）： 10-14.

[9]? ?吳亮秦， 吳定俊， 李奇. 城市軌道交通橋梁列車制動力試驗研究[J]. 鐵道學報， 2012， 34（3）： 88-93.

WU L Q， WU D J， LI Q. Experiment study on braking force for urban rail transit bridge[J]. Journal of the China Railway Society， 2012， 34（3）： 88-93.

[10]? 程杰. 無支座連續剛構軌道結構受力分析及溫度跨度研究[D]. 北京： 北京交通大學， 2015.

CHENG J. Analysis of track structure and research on temperature span of continuous rigid frame without supports[D]. Beijing： Beijing Jiaotong University， 2015.

[11]? MA Y R， CHEN H B， HAN Q W. Sensitivity analysis of factors affecting down deflection of long-span continuous rigid frame bridge[J]. Earth and Environmental Science， 2021， 781（2）： 022048.

[12]? YAN Y H. The effect of foundation differential settlement on mechanical properties of continuous rigid frame bridge[J]. International Journal of Civil Engineering and Machinery Manufacture， 2017， 2（3）： 973-991.

[13]? LI Y L， WU X G. Study on optimal calculation model for high piers of rigid frame bridge under pile-soil effect[J]. Engineering and Applied Sciences， 2019， 3（6）： 134-144.

[14]? 朱志輝， 李曉光， 閆銘銘， 等. 基于扣件阻力試驗的高速鐵路橋上無縫線路縱向力研究[J]. 中南大學學報（自然科學版）， 2020， 51（7）： 1966-1976.

ZHU Z H， LI X G， YAN M M， et al. Longitudinal force of CWR on high speed railway bridge based on fastener resistance test[J]. Journal of Central South University （Science and Technology）， 2020， 51 （7） ： 1966-1976.

[15]? 羅華朋， 邢俊， 楊凱， 等. 橋墩溫度梯度對高墩大跨橋上無砟軌道影響研究[J]. 鐵道標準設計， 2015， 59（8）： 26-29.

LUO H P， XING J， YANG K， et al. Effects of pier temperature gradient on ballastless track of long-span bridge[J]. Railway Standard Design， 2015， 59（8）： 26-29.

[16]? 王偉華. 城際鐵路4×40 m連續剛構橋與無縫線路相互作用研究[J]. 中國鐵路， 2023， 30（4）： 100-107.

WANG W H. Research on the interaction between 4×40 m continuous rigid frame bridge and CWR of intercity railway[J]. China Railway， 2023， 30（4）： 100-107.

[17]? 王冬梅， 倪向陽， 王慧珺. 城市軌道交通雙線橋上無縫線路撓曲力研究[J]. 都市快軌交通， 2012， 25（6）： 96-99.

WANG D M， NI X Y， WANG H J. Analysis of the flexural Forces in CWR on double-track bridges of urban rail transit[J]. Urban Rapid Rail Transit， 2012， 25（6）： 96-99.

第一作者：張鵬飛（1975—），男，教授，博士，博士生導師，研究方向為橋上無縫線路設計理論與關鍵技術。E-mail：zhangpf4236@163.com。

通信作者：胡達貴（1997—），男，碩士研究生，研究方向為橋上無縫線路。E-mail：1463492008@qq.com。